具有时间相关系数和双参数扰动的捕食者-食饵模型分析*
2022-01-05魏宁
魏 宁
(南京财经大学 应用数学学院, 南京 210023)
0 引 言
在种群生态学的研究中, 捕食者和食饵之间的动力学关系是生物数学界研究的重要课题之一。近年来, 许多学者都致力于研究具有各种功能反应的捕食者-食饵模型, 其中具有Holling Ⅱ型功能反应的捕食者-食饵模型受到了广泛关注[1-3]。如2003年,Aziz-Alaoui等[2]讨论了具有改进的Leslie-Gower和Holling-II型方案的随机捕食者-食饵模型解的存在性和全局稳定性的动力学行为;2017年,Nosrati等[3]通过分数演算和经济理论, 扩展了一个更现实的捕食者-猎物模型: 具有Holling II型功能响应的分数阶奇异捕食者-被捕食模型, 并从局部稳定性的角度研究了该模型的动力学行为。
上述文献讨论的都是确定性的捕食者-食饵模型, 但在实际的生态系统中, 环境干扰是种群系统中不可忽略的重要组成部分。对此, 许多学者将随机扰动引入到确定性模型中来探究环境扰动对种群系统的影响。如2005年,Jiang等[4]考察了在增长率上具有随机噪声的单种群模型, 证明了该模型具有唯一的全局解, 并给出了解的显示表达; 2015年,Liu等[5]讨论了一类具有随机扰动的三种群捕食系统,分析了系统的稳定性并给出了灭绝的充分条件;Liu[6]考虑了环境波动对内禀增长率和死亡率的影响, 提到了下列带有随机扰动的Holling II捕食者-食饵种群模型:
(1)
其中,x(t)和y(t)分别表示在t时刻食饵和捕食者种群的数量;ri,bi,ci(i=1,2)都是正常数,r1表示种群x(t)的内禀增长率,r2表示种群y(t)的死亡率,b1和b2分别表示x(t)和y(t)的密度制约系数,c1和c2分别表示捕食者的捕食率和其营养物转化为繁殖率的转化率。
目前, 在研究随机生物数学模型时, 大部分文章只讨论了环境噪声对其中某一类参数的影响[4-6]。然而, 在生态系统中, 环境扰动会对种群的捕食率、种内和种间竞争系数等多种参数同时产生影响。因此,为了使模型更贴合实际并能更准确地掌握种群数量变化规律, 本文在模型式(1)的基础上又考虑了环境波动对种群密度制约系数b1和b2的影响, 并用以下方式表示:
-b1→-b1+σ12dB2(t)
-b2→-b2+σ22dB4(t)
另一方面, 在实际情形中, 受季节变化的影响, 生态系统中的温度和湿度等机制会随之发生改变, 进而导致种群的繁殖率和死亡率等参数会随时间的变化而变化。 例如: 某些鸟类动物的卵在孵化时, 在最适的温度下繁殖率最高, 离开了最适温度,繁殖强度就会下降, 甚至停止繁殖。对此, 可引入与时间t相关的系数来描述这一现象。针对具有时间相关系数的种群模型已有大量的研究[7-8]。但文献[7-8]仅仅是针对具有单个随机扰动的模型系统, 而对于具有双参数扰动的Holling II捕食者-食饵模型的研究几乎都假设种群出生率等参数与时间t无关。对此, 为了使模型更具有现实意义, 得出更精确的结论, 本文还把与时间t相关的系数引入到模型式(1)中, 进而建立了下列具有可变系数的双参数扰动随机模型:
(2)
其中,Bi(t)(i=1,2,3,4)是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上相互独立的布朗运动;σij(t)>0(i,j=1,2)表示白噪声强度;ri(t),bi(t),ci(t),σij(t)(i,j=1,2)是R+:=[0,+∞)上非负且有界的连续函数。定义:
同样的符号也应用于bi(t),ci(t),σij(t)(i,j=1,2)。
接下来的章节依次研究了式(2)正解的存在唯一性、随机最终有界性、一致连续性、随机持久性和灭绝的充分性条件。
1 解的存在唯一性和随机最终有界性
为了研究式(2)的长时间动力学行为, 首先要证明式(2)具有唯一的全局正解。
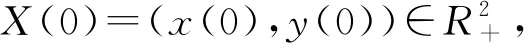
证明类似于文献[4]中定理1的证明方法, 容易得到定理1成立。
对随机种群系统的研究中, 通常不满足于其非爆炸性质, 因此, 本节进一步研究了其随机最终有界性。
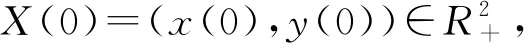
证明定义函数U(x)=etxp, 其中p∈(0,1), 利用It公式可得:
d(etxp)=etxp{1+p[r1(t)-b1(t)x)-
σ12(t)petxp+1dB2(t)
(3)
利用Young’s不等式, 有
(4)
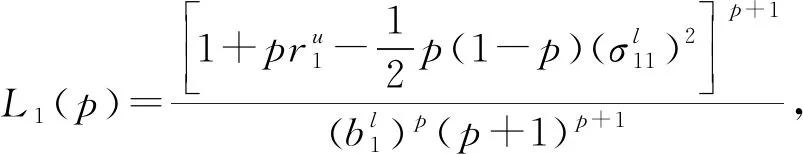
xp(0)+etL1(p)
因此,
(5)
同理可得:
(6)
根据式(5)和式(6), 以及基本不等式(x(t)+y(t))0.5p≤20.5p(x(t)+y(t)), 有
20.5p(L1(p)+L2(p)):=L(p)
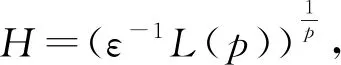
P{|X|≥H}≤H-pE|X|p
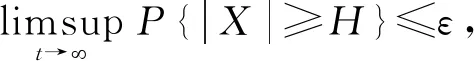
2 一致Hölder连续和随机持久性
在种群动力学行为研究中, 一致连续性和随机持久性是研究的重要性质之一, 对物种保护等方面具有重要意义。一致连续性表示种群会以适度方式繁殖, 在任何时刻都不会激增; 随机持久性表示种群会永久持续生存。本节首先讨论了式(2)正解的一致Hölder连续性。
定理3 设X(t)是式(2)对于任意正的初值X(0)=(x(0),y(0))的正解, 那么X(t)的几乎所有样本路径都是一致Hölder连续的。
证明参照文献[10]中定理6.3的证明方法,式(2)中第一个方程可以转换为下列随机积分方程:
由式(5)和定理2, 以及离散Hölder不等式[9], 可得:
22p-2L1(2p):=L11(p)
且有
利用矩不等式[9], 有
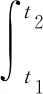
其中,0≤t1≤t2, 且p>2。因此, 利用离散Hölder不等式, 有
E|x(t2)-x(t1)|p≤
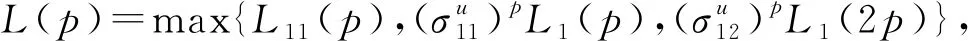
接下来证明式(2)的随机持久性。
定理4 式(2)是随机持久的。
证明受文献[12]中证明方法的启发,取某一正常数η<1, 定义函数:
Z(X)=η-1(1+x-1)η+η-1(1+y-1)η
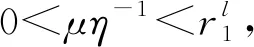
(7)
其中,
显然H1<+∞, 对式(7)两边从0到t积分并取期望, 有
E[F(X)]=eμtE[Z(X)]≤
η-1(1+x-1(0))η+η-1(1+y-1(0))η+
μ-1H1(eμt-1)
因此,
μ-1ηH1=H
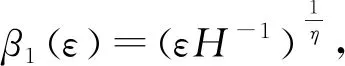
同理可得:
则有
进一步得到:
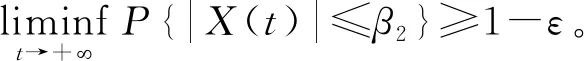
3 灭绝性
本节讨论式(2)灭绝的充分性条件。
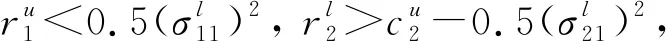
证明受文献[13]中证明的启发, 令u(x(t))=lnx(t), 利用It公式, 有
σ11(t)dB1(t)+σ12(t)x(t)dB2(t)
对上式两边从0到t积分, 得
lnx(t)-lnx(0)=
(8)
由Borel-Cantelli引理[9]可知, 存在Ω0⊆Ω满足P(Ω0)=1, 使得对任意ω∈Ω0, 都存在整数T0=T0(ω)>0, 当T≥T0且0≤t≤T时, 有
M1(t)≤2lnT+0.5〈M1(t),M1(t)〉=
(9)
把式(9)代入式(8)并取上极限,得
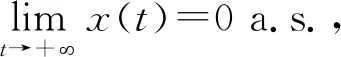
由定理5得到的种群灭绝的充分性条件可知, 模型式(2)中的种群灭绝与参数σ12(t)和σ22(t)无关, 这表明环境噪声对种群密度制约系数的影响不会导致模型式(2)中的种群灭绝。
4 数值模拟
本节利用Milstein方法[14]对式(2)进行数值模拟, 来验证理论分析结果。选取步长为Δt=0.001, 初值为(x(0),y(0))=(0.3, 0.5),r1=1.2+sin(t),r2=0.1+cos(t),b1=0.9,b2=0.7,c1=0.8,c2=0.7,通过只改变随机扰动系数σ11(t),σ12(t),σ21(t)和σ22(t)的取值来观察种群数量的变化情况, 得到如图1所示的结果。
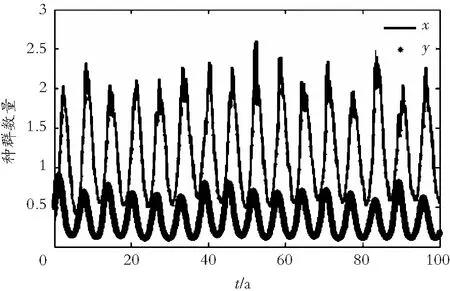
(a)σ11(t)=σ12(t)=σ21(t)=σ22(t)=0
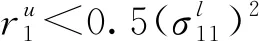
5 结束语
在具有一个环境噪声的Holling II捕食者-食饵模型的基础上, 考虑了具有两个环境噪声且模型系数与时间有关的Holling II捕食-食饵模型, 使模型系统更贴合实际。证得了模型正解的存在唯一性和随机有界性, 探究了模型的持续性和随机持久性, 并给出了模型中种群灭绝的充分性条件, 从而掌握了更准确的种群数量变化规律, 对物种保护、利用和管理具有重要意义。
