随机常微分方程的几种数值求解方法及其应用*
2022-01-05李焕荣
李 焕 荣
(重庆工商大学 数学与统计学院,重庆 400067)
0 引 言
近十年以来,随机数学模型[1]的研究在很多欧美国家已经得到了高度重视和大力发展, 吸引了大批应用数学家和计算数学家的关注, 随机数学模型的数值求解方法[2-4]和理论分析也得到了快速的发展。目前, 随机数学模型在美国已经成为最重要的应用数学和计算数学的研究方向之一。美国很多部门比如能源部、空军和国家实验室,均设立了专项基金来支持和发展随机数学模型的数值计算、理论分析和相关应用等研究工作。
随机常微分方程(Stochastic Ordinary Differential Equation, 简写为SODE)是近几十年来才兴起的热门边缘学科,是概率论与常微分方程(Ordinary Differential Equation, 简写为ODE)相结合的产物,自日本数学家伊藤清[5](It)先生于20世纪40年代创立随机积分(It积分)以来,随机微分方程很快就被广泛应用到金融经济、自然科学和工程技术等很多领域,如股市预测、资料同化、油藏模拟、天气预测、流体动力学和生物遗传学等。汤涛院士等[1]从不确定性量化的角度讨论了随机数学模型的发展近况; Markos[2]讨论了随机相场模型Allen-Cahn的噪声正则性和相关计算;伊藤清[5]讨论了随机微分方程的推导以及它和确定性微分方程的关系。但求随机微分方程的精确解却是非常困难的,因此本文将讨论求解随机微分方程数值解(近似解)的方法,并应用实例验证比较几种数值方法的优劣。
先从一阶常微分方程解析解的求解出发,对比了常微分方程几种经典的数值求解方法:欧拉方法、改进的欧拉方法、三阶Runge-Kutta公式和四阶Runge-Kutta公式,并举例编程可视化对比了精确解(或解析解)和相应的数值解;然后从It随机微分方程[5]的产生出发,举例图示对比了在不同布朗运动影响下的随机常微分方程精确解和相应的确定性(deterministic)常微分方程精确解的差别;最后给出了随机常微分方程的3种数值求解方法[6]:Euler-Maruyama方法、Milstein方法和 Runge一Kutta方法,并举例图示对比了不同布朗运动下的3种数值方法的求解结果。
1 常微分方程的数值方法
先介绍常微分方程的解析解求解,再给出经典的数值求解方法。
1.1 解析解
17世纪末,牛顿划时代的巨著《自然哲学的数学原理》面世了,从此微分方程便诞生了。大多数数学家们一开始都努力去寻找微分方程的解析解(精确解),从而试图去解释由微分方程所描绘的物理规律和自然现象。数学家们在此方面也确实取得了一系列较成熟的成果,比如一阶常微分方程:
(3) 恰当微分方程M(x,y)dx+N(x,y)dy=0。
还有二阶常系数线性微分方程:
都得到了较成熟的求解方法。
1.2 数值解法
但是,到了18世纪60年代,数学家们渐渐意识到绝大多数的微分方程是无法求得它们的解析解的,于是人们才逐渐认识到从另外一个角度来研究微分方程的解,即数值解,是十分有必要的。其中,瑞士数学家欧拉在数值求解方面就做出了开创性的工作。1768年,欧拉有关月球运行理论的著作出版了,创造了后来被广泛应用于求解常微分方程初值问题数值解的方法,即被人们后来称道的Euler(欧拉)方法。一阶常微分方程的欧拉方法主要有向前的欧拉方法:
yn+1=yn+hf(xn,yn),n=0,1,2,…
向后的欧拉方法:
yn+1=yn+hf(xn+1,yn+1),n=0,1,2,…
改进的欧拉方法:
其中,改进的欧拉方法在解决实际问题中最为常用。
Euler方法是求解常微分方程初值问题的最简单数值方法,但它的收敛阶偏低,向前和向后的欧拉方法仅仅一阶精度,改进的欧拉方法的精度虽然提高到了二阶,但对于更复杂的实际问题,二阶精度却还是不够的。于是,在1895年,德国数学家Runge在改进的欧拉方法基础上发表了《常微分方程数值解法》,此文章成了高精度数值求解常微分方程Runge-Kutta方法的开端, 在常微分方程数值方法发展史上具有里程碑意义。Runge-Kutta方法在创立之时并未达到完善,后来又经过大量数学家们多年的共同努力才逐渐完善成熟,目前常用的有三阶Runge-Kutta公式:

四阶Runge-Kutta公式:
关于其他的常微分方程数值解法,限于篇幅有限,就不在此赘述。
1.3 应用比较
下面分别用向前的欧拉方法、改进的欧拉方法、三阶Runge-Kutta公式和四阶Runge-Kutta公式数值求解下列方程:
这是伯努力微分方程,通过变量变换可转化为非齐次线性微分方程,从而利用常数变易法可以得到方程的解为
过点(0,1)的解,即满足初始条件的精确解为
从图1的比较可以看出,用向前的欧拉方法( 图1(a))和改进的欧拉方法(图1(b))求出的数值解与精确解(The exact solution)的误差较大,而用三阶Runge-Kutta公式(图1(c) )和四阶Runge-Kutta公式(图1(d))求出的数值解与精确解的误差较小,尤其是四阶Runge-Kutta公式求出的数值解与精确解几乎是完全重合的(图1(d)),这些数值结果与理论分析是完全一致的。
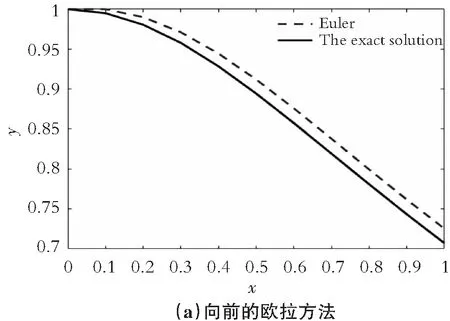
图1 常微分方程的4种数值方法
2 随机微分方程
2.1 It随机微分方程
当忽略掉一些比较次要的影响因素,用确定性微分方程[7-8]来试图描述自然现象的时候,实际上得到的解释是不完全准确的。目前,随着高速计算机的产生和对科学研究的深入,以及对自然现象描述解释准确度要求的提高,必须重新考虑那些曾经被忽略掉的随机因素。科学家们也逐渐认识到,随机因素不仅仅是对确定性模型存在缺陷的一个补充,很多情况下更是反映了物理规律和自然现象的内在本质。于是借助于概率论这一工具, 科学家们将忽略掉的随机因素统一建模成随机变量,随机微分方程的理论研究和数值研究就势在必行了[1]。1951年,日本数学家It发表了影响整个数学界的关于随机微分方程的学术论文,自此才有了对随机因素严格意义上的数学描述.
引入Wiener过程的定义[5]。
定义1 如果一个实值随机过程W(·)满足下列3个条件:
1)W(0)=0;
2)对所有0≤s≤t,都有W(t)-W(s)服从分布N(0,t-s);
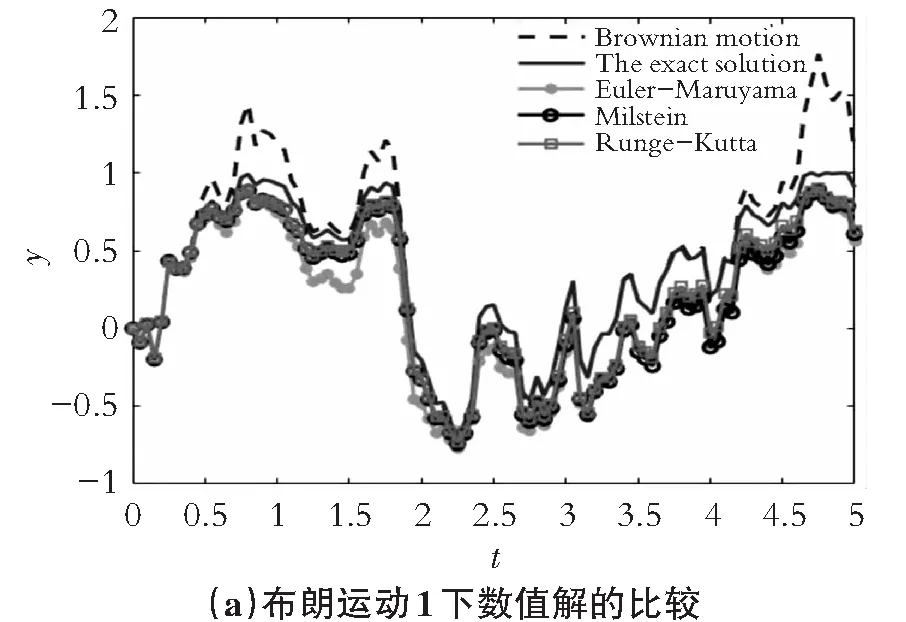
3) 对所有0 尽管Wiener过程和实验相符,但它只是对真实布朗运动的理想化表述,和牛顿力学相距甚远。1930年, Uhlenbeck和Ornsteinv 从牛顿力学的角度系统地解释和发展了布朗运动的动力学理论。 以y(t) 表示作布朗运动的粒子在时刻t的速度,m表示粒子的质量。根据牛顿定律,可以得到如下方程: dy(t)=-βy(t)dt+σdW(t) (1) 这里,-β为漂移系数,σ为扩散系数,W(t)则是Wiener过程。 若已知初始速度y0,将式(1)写成如下积分方程形式: 当σ和-βy(t)均依赖于布朗运动的粒子速度及时间t时,就得到了如下的It随机积分方程: 将其写成微分形式: dy(t)=f(t,y(t))dt+g(t,y(t))dW(t) (2) dy(t)=-ry(t)dt+σydW(t) (3) y(0)=1 其中,r和σ为正常数,在这里取r=σ=1。该随机微分方程其满足初始条件y(0)=1的解析解为 随机微分方程式(3)对应的确定性常微分方程为 其满足初始条件y(0)=1的解析解为 y=e-rt 是关于时间t的一条指数型曲线。 在图2(a)和2(b)中可以看到,在连续的布朗运动(Brownian motion)即随机Wiener过程的影响下,随机微分方程(SODE)的精确解在区间[0,3]上,偏离了相应的确定性常微分方程(ODE)的精确解, 受布朗运动(虚线)影响较大,后面区间上影响较小。 图2 It随机常微分方程(SODE)和相应的确定性常微分方程(ODE)的精确解 在这一节重点介绍几种经典的求解随机微分方程的数值方法。 yn+1=yn+f(yn)Δt+g(yn)ΔWn (4) 其中,ΔWn=Wtn+1-Wtn表示定义在区间[tn,tn+1]上的Wiener过程的增量,是服从N(0,Δt)分布的相互独立的随机变量。该欧拉格式的强收敛阶只有0.5。 Milstein方法:1974年, Milstein给出了求解随机常微分方程式(3)的具有一阶强收敛的Milstein方法 ,即 yn+1=yn+f(yn)Δt+g(yn)ΔWn+ Runge-Kutta方法:1982年, Rümelin将Runge-Kutta方法发展到随机微分方程,构造了求解式(3)的一阶强收敛的随机Runge-Kutta方法,其一般格式为 下面,举例给出上述3种方法[6]数值求解的结果比较。考虑如下随机微分方程: (5) 该随机微分方程式(5)满足初始条件的精确解为 y=sinWt 在这里,只给出用Euler-Maruyama方法数值求解随机微分方程式(5)的算法,其他两种可类似得到。 Euler-Maruyama算法: 给定y0,n=0,1,2,…,有 图3 随机微分方程的数值方法与精确解的比较 在图3的4个图中,虚线均表示连续的布朗运动轨迹(Brownian motion),即随机Wiener过程;实线均表示随机微分方程式(4)的精确解(The exact solution),余下3条线分别表示用Euler-Maruyama方法、Milstein方法和Runge-Kutta方法得到的数值解。从图3可以看到,Milstein方法和Runge-Kutta方法得到的数值解几乎完全重合,与精确解的偏差较小,这是因为Milstein方法和Runge-Kutta方法都是一阶强收敛的。而从4个图整体来看,Euler-Maruyama方法得到的数值解偏离精确解较多,这是因为Euler-Maruyama方法的强收敛阶只有0.5,这些都与理论分析完全吻合。 先从一阶常微分方程解析解的求解出发,对比了常微分方程的几种经典数值求解方法:欧拉方法、改进的欧拉方法、三阶Runge-Kutta公式和四阶Runge-Kutta公式,并举例编程可视化对比了精确解和相应数值解的偏差,以此说明他们的不同和优势;其次从It随机微分方程的产生出发,举例对比了随机常微分方程精确解和相应的确定性(deterministic)常微分方程精确解的差别,以此看到随机布朗运动对微分方程解的影响;最后给出了随机常微分方程的3种数值求解方法:Euler-Maruyama方法、Milstein方法和 Runge-Kutta方法,并举例图示对比了不同布朗运动下的3种数值方法的求解结果以及与精确解的偏差,实验结果与理论分析也完全吻合。本文对随机微分方程的学习和数值解的求解及应用都有一定的指导意义。2.2 举例对比

3 随机微分方程的数值方法
3.1 几种数值方法
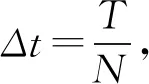
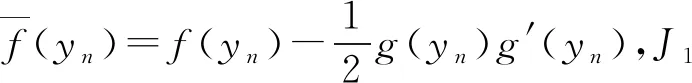
3.2 应用比较

4 小 结
