具有标准发生率的随机SIRS传染病模型的趋势分析
2022-01-05赵亚男
夏 兰, 赵亚男
(1.吉林交通职业技术学院基础部,吉林 长春 130012;2.长春大学理学院,吉林 长春 130022)
1 预备知识
2020年初,新型冠状病毒性肺炎疫情在全球爆发,给全世界人民的健康带来了巨大的威胁,也严重影响了我们的经济活动和日常生活.利用数学建模分析传染病的发展、传播和控制越来越受到人们的关注,为如何制定合适的防控措施和科学决策提供定量依据.
众所周知,自然科学、工程与应用科学中的复杂系统的运动变化规律通常用微分方程来描述.然而,在实际应用中,复杂的系统会受到随机扰动、随机环境、随机边界条件、随机输入和随机初始条件等因素的影响,这些可以通过随机过程来描述或近似.在随机因素的影响下,随机动力学系统是更适合这些复杂系统的数学模型,这可能会对系统的演化产生微妙的影响.在今年疫情的大环境下,随机传染病系统的动力学行为也越来越受到学者们的关注[1-4].
在传染病建模中,疾病发生率函数可以合理地描述流行病的传播.[5-7]在许多流行病学模型中,相对于易感和感染个体的数量,相应的发病率一般是双线性的[6,8],但当人口数量很大时,与人口成正比的接触率显然是不符合实际的,通常对人类和某些群居的动物来说,与双线性发生率相比,标准发生率更符合实际情况.Busenberg等[9]讨论了一个经典的SIRS传染病模型:
(1)
其中:S(t),I(t)和R(t)分别表示t时刻易感者、感染者和康复者的数量;总人口N(t)=S(t)+I(t)+R(t),满足N′=(b-μ)N-αl;b表示出生率;μ是自然死亡率;β表示接触率;δ表示康复者的免疫丧失率;α表示感染者的因病死亡率;γ表示感染者的恢复率.所有参数均假定为非负且b,γ>0,模型分析得到的阈值
(2)
决定了该流行病将灭绝,或者持续的趋势.根据Busenberg等[9]的理论研究,有:
(a) 无病平衡点(1,0,0)始终存在.当R0≤1时,在可行区Γ中全局渐近稳定;当R0>1时,它是不稳定的,这里Γ={x≥0,y≥0,z≥0|x+y+z=1}.
(b) 当R0>1时,存在唯一的地方病平衡点,在Γ0中全局渐进稳定,这里Γ0=Γ-{(1,0,0)}.
记
介绍采用种群类别比例的方法,即作比例函数
x=S/N,y=I/N,z=R/N.
(3)
相对于较为严格的方法要求感染总数I(t)→0,这里只需考虑较弱的要求比例y(t)→0.
实际上,流行病不可避免地受到环境白噪声的影响,环境白噪声是现实中的重要组成部分.本文考虑将SIRS流行病模型的结果推广到随机环境,研究随机环境中疾病发展趋势与基本再生数(阈值)的关系,且进行了严格的理论推导.将随机性引入模型(1)[10-11],得到:
(4)
其中:B1(t),B2(t),B3(t)是独立的布朗运动;σ1,σ2,σ3是其强度;总人口N(t)满足
dN(t)=[(b-μ)N(t)-αI(t)]dt+σ1S(t)dB1(t)+σ2I(t)dB2(t)+σ3R(t)dB3(t).
(5)
应用x=1-y-z,容易验证y和z满足微分方程
(6)
随机微分方程的一些基本理论参见文献[12].在本文中,(Ω,{Ft}t≥0,P)是一个完备的概率空间,具有流{Ft}t≥0,满足通常条件(即右连续和{F0}包含所有零测集).B(t)是概率空间上定义的一个标量布朗运动.
2 正解的存在唯一性
在研究动力学行为之前,要考虑随机系统解是否全局存在.由于系统(6)的系数不满足线性增长条件,因此可能会在有限的时间内爆破[12].在本节中,使用Lyapunov分析方法[2],证明系统(6)的解是全局正解.令不变集
(7)
定理2.1 对于任意给定初值(y(0),z(0))∈D,随机系统(6)存在唯一的解(y(t),z(t))∈D,t>0,并且解将以概率1保留在D中,即对所有的t>0,有(y(t),z(t))∈D,a.s..
证明定义C2-函数V:D→[0,R+),
V(y,z)=(y-1-logy)+(z-1-logz)+[(1-y-z)-1-log(1-y-z)],
利用伊藤公式,得

其余部分参见Gray等[2]解的存在唯一性的标准证明过程.
3 灭绝性
定理3.1 对于任意初值(y(0),z(0))∈D,令(y(t),z(t))为随机系统(6)的解,则
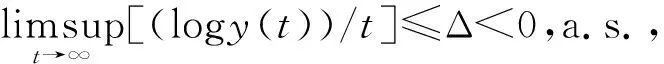
(8)
其中

(9)

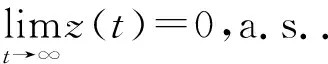
(10)
证明应用伊藤公式于系统(6),有

(11)
两端同时积分并除以t,得到
(12)

两端取上极限,得
(13)
如果0<λ<(b+γ),通过(12)式得
下面证明结论(10).根据系统(6)的最后一个方程,有

其中:
(14)
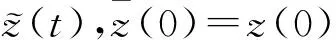
从而
其解为
(15)
其中

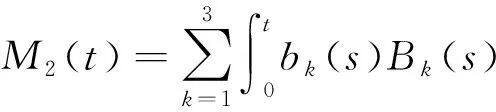
通过(9)式和M2(t)轨迹是连续的,表明存在一些零测集N,使得P(N)=0,并且对于任何ω∉N,M2(·,ω)是连续的,得
这里Δ被定义为(9)式.因此,对于任何ε>0,存在T=T(ω),使得
y(t,ω)≤exp((Δ+ε)t),∀t≥T.
故对于所有ω∈Ω,如果t>T(ω),通过(15)式,有



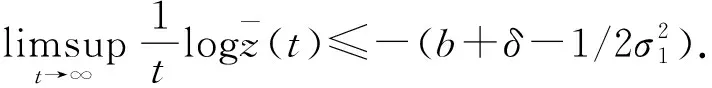
定理3.1揭示了当满足一定条件时,感染者比例函数长时间行为趋于0,表示疾病趋于灭绝.
4 持续性

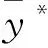
证明根据系统(6),有
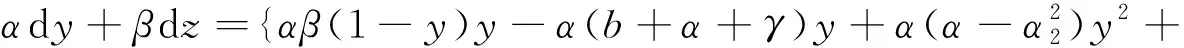
(16)
这里

若满足定理4.1的条件,有

计算得
(17)

因为0 (18) 根据(11)式的第2个等式,有 将其从0到t积分并两边除以t,得到 因此得到 根据(6)式最后的等式得 其中bk(t)由(14)式定义,则 这里根据Khasminskii[14]的理论证明存在平稳分布且是遍历的,是一种弱稳定性,表明该疾病也将流行. (19) 不难知道f(y,z)在(rθ,1-(r+1)θ)处达到最大值,这里 f(y,z) LV=LV1+LV2+LV3+LV4, 其中 则 定义一个封闭的集合 Uε,k={(x,y)∈D|ε≤x≤1-ε,ε≤y≤1-ε,x+y≤1-k}, 这里ε,k>0和ε2=k,使它们尽可能的小,满足: rεβ(1+(α+γ)/(b+δ))<1, (20) (21) (22) 令: 那么 由(21)式,得到LV(x)<-1. 使得 从而Hasminskii[14]提出的条件(B.1)满足.因此,随机系统(6)具有平稳分布μ(·),且是遍历的. 本文分析了具有标准发病率的随机SIRS传染病模型,分析结果表明随机系统(6)存在唯一的正解.在满足条件(9)的情况下,流行病将趋于灭绝.当满足定理4.1条件时,流行病将长时间持续发生.定理5.1给出流行病系统在持久情况下的遍历行为,存在平稳分布.本文结果对流行病防治提供参考性建议.


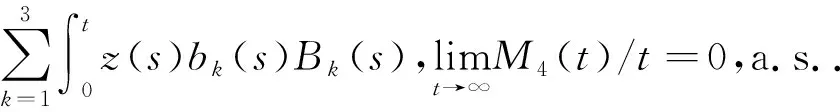
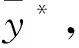
5 遍历性



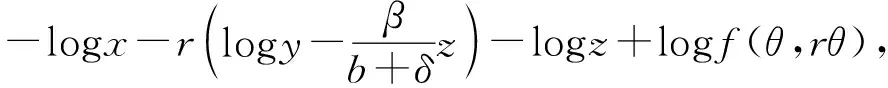
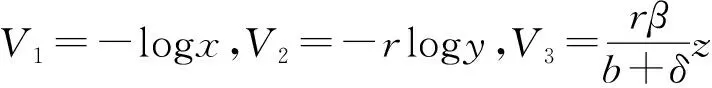
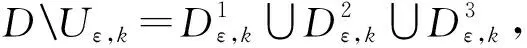



6 结 论
