基于核非负矩阵分解的有向图聚类算法
2022-01-05胡丽莹林晓炜陈黎飞
陈 献,胡丽莹*,林晓炜,陈黎飞,3
(1.福建师范大学计算机与网络空间安全学院,福州 350117;2.数字福建环境监测物联网实验室(福建师范大学),福州 350117;3.福建省应用数学中心(福建师范大学),福州 350117)
(∗通信作者电子邮箱hlyxyz@fjnu.edu.cn)
0 引言
图结构可以自然地表示网状结构的数据,如社交网络、电力网络、引文网络、运输网络、蛋白质-蛋白质相互作用网络[1]等。随着各个领域网络数据的增长以及对网络数据处理的迫切需求,分析图结构以及挖掘图结构中的关系信息成为了热点问题,图聚类[2]是其中的一项基础研究课题。图聚类根据节点及节点间连接关系的相似性将节点划分为簇,使得簇内节点相似度较高,簇间的节点则差异较大。
目前已提出多种图聚类算法,包括基于图分割的算法[3]、层次聚类算法[4]、谱聚类算法[5]等,这些算法大多忽视节点连边的方向性,把有向图转化为有无向图进行处理。对于有向网络如引文网络、基因转移网络、运输网络等,若以无向图方式处理将丢失有用信息甚至引发歧义。例如,对于由文献间引用和被引用关系构成的引文网络,当看作无向图时,将出现文献间仅存在的单方面引用关系变成同时包含引用和被引用双向关系的错误情形。为有效建模节点间连接关系的方向性,目前典型的方法是将无向图聚类算法推广到有向图,如Satuluri 等[6]提出的转换有向图为无向加权图的方法,通过有向图上非对称邻接矩阵随机游走对称化或节点的入度和出度对称化手段来构造新的对称邻接矩阵,但这种方法可能导致有向图上某些独特的边方向性信息丢失。基于Laplacian 矩阵的多种谱聚类算法[7-9]则将聚类目标函数扩展到有向图中,并对得到的拉普拉斯矩阵做特征值分解;但该矩阵的特征值可能存在负值,降低了所构造模型的可解释性。
基于非负矩阵分解(Nonnegative Matrix Factorization,NMF)[10]的一类方法[11-12]则通过将图邻接矩阵的非负结构分解(structured factorization)实现图聚类。由于被分解的可以是非对称矩阵且分解结果均为非负矩阵,该类方法对有向图聚类具有良好的适应性和可解释性,近年来得到广泛关注。譬如,Wang 等[11]提出的非对称非负矩阵分解(Asymmetric NMF,ANMF)算法将有向图的非对称邻接矩阵分解为分别表示“节点-簇”隶属度和簇间相似性的非负矩阵,进而基于隶属度矩阵对节点进行簇划分;在此基础上,Tosyali等[12]引入节点间的相似先验信息为正则项,构造了正则化的非对称非负矩阵分解(Regularized Asymmetric NMF,RANMF)算法,提高了有向图聚类的准确性和鲁棒性。
然而,以上算法忽略了有向图上潜在的节点间的非线性关系。在许多实际应用产生的图(网络)中,节点与节点之间通常是非线性相关的。如社交网络中,个体(节点)之间的关系并不是单一的,有可能是同事、家人甚至更复杂的人际关系(有向边)。显然,这些关系不能简单地以线性方式来逼近。当前,深度学习(deep learning)与核学习(kernel learning)是两种主流的节点间非线性关系建模方法。例如,Perozzi 等[13]提出深度游走(DeepWalk)算法,通过随机游走捕捉图的高阶近邻结构,进而将深度学习技术运用到图聚类问题中;但是,该算法并未考虑节点间连接的方向性。核学习方法[14]通过将低维数据嵌入到高维核空间中,使得低维不可分数据在新空间中线性可分或接近线性可分,从而有效挖掘隐含在数据中的非线性关系。近年,已提出多种核非负矩阵分解(Kernel NMF,KNMF)算法,利用小样本条件下核学习方法在非线性学习中的良好性能进行人脸识别、文本聚类等[15-18]。
本文提出用于非线性有向图聚类的核非负矩阵分解算法,称为正则化的核非对称非负矩阵分解(Regularized Kernel Asymmetric NMF,RKANMF)。首先,基于核化机制构造了有向图核聚类目标函数,定义了约束核空间中节点相似性关系的正则化项,以保持原空间中节点间相似关系的同时强化核空间中同簇节点间的(非线性)相似性;其次,基于梯度下降法提出了一种聚类优化算法,证明了算法的收敛性;最后,在8个有向网络数据集上进行了实验,并与深度学习算法等进行了对比,实验结果验证了所提算法的有效性。
1 相关工作
1.1 基本定义
定义1有向图。在有向图中G=(V,E),边(i,j)∈E将节点i连接到节点j,|V|表示节点数,|E|表示边数。有向图可以由邻接矩阵来表示。
构建有向图邻接矩阵:邻接矩阵A∈Rn×n+,其中n是节点数,若从节点到节点存在有向边,[A]ij=1,否则[A]ij=0。特别地,[A]ii=0。本文用[·]ij表示矩阵第i行第j列元素。
图聚类基于节点间的相似性:节点之间越相似,则越可能划分到同一个簇。文献中常用的节点相似性度量有:
1)Katz 中心相似性度量[19]。对于图中每一条路径,利用加权方案计算其权重,公式如下:

其中:I为元素全为1 的矩阵;当参数β<1 时,较长的路径将分配到较小的权重,较短的路径则获得更大的权重,权重越大,节点间就越相似。
2)余弦相似性度量[19]。计算节点间公共邻居的数量,公共邻居的数量越多表示节点间越相似。计算公式为:

其中:cij表示节点i与节点j的公共邻居数量;为由所有邻居数量组成的向量的长度,取值在0到1之间。余弦相似度为1表示两个节点具有相同的邻居,0则表示没有相同邻居。
1.2 基于NMF的聚类算法

其中:r≪min{m,n}为分解矩阵的秩;‖⋅‖F表示矩阵的Frobenious 范数。对于聚类任务[20],分解结果中的W可以视为隶属度矩阵,根据规则将第i个样本xi分配到隶属度最大的簇j*,完成聚类。
下面介绍两种基于NMF 的代表性有向图聚类算法:ANMF[12]和RANMF[13]算法。ANMF 将式(3)中的B矩阵用HWT代替,其中,,定义其优化问题如下:
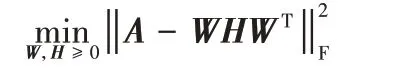
RANMF 在ANMF 算法基础上添加了图正则化项,对同簇节点间的相似性进行约束,其定义的优化问题如下:
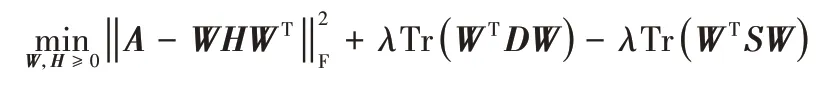
其中:Tr(⋅)是矩阵的迹;S是节点间相似性矩阵;D为对角矩阵,其中每个对角元Dii是矩阵S的第i行元素的和。
1.3 核函数与KNMF
核函数是从低维空间到高维空间中的一种映射函数。设R为输入空间,H为特征空间(希尔伯特空间或核再生空间,以下简称核空间),核学习方法[14]利用核函数实现从R到H的映射:φ(X):R→H。对于输入空间的样本对(xi,xj),核技巧(kernel trick)通过替换核空间中样本对的内积为核函数κ(xi,xj)的值(核化),解决φ(X)难于计算的问题,即:
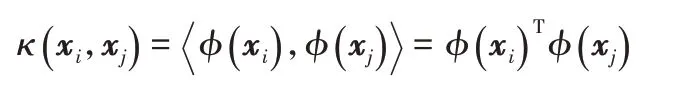
常用的核函数包括多项式核函数和径向基核函数等,其定义分别如下:
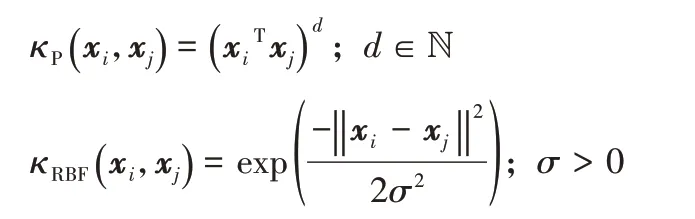
为捕捉数据中的局部结构信息,文献[21]新近提出了分数阶核(Fractional power kernel):
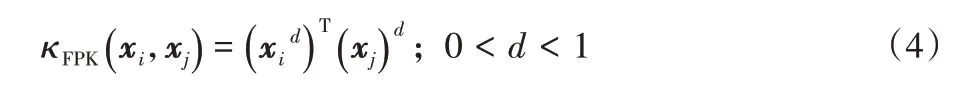
其中:zd表示任意向量z中每个元素的d次幂。鉴于图聚类的目的在于根据图的局部结构特性进行节点分组,本文采用如式(4)所示的分数阶核函数,并用矩阵形式加以表示,如下:
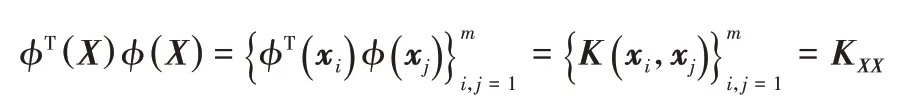
在传统NMF 的基础上,利用上述核化机制可以对输入矩阵进行核非负矩阵分解(KNMF)。例如,基于KNMF 的人脸识别[17-18]定义其优化问题为:

意在优化两个非负矩阵W和B,使得映射后的人脸图像在核空间可以近似地表示为基图像的线性组合,即:φ(X)≈φ(W)B。相比仅能对数据中线性关系建模的传统NMF,KNMF 的优势在于可以通过核函数对数据进行高维映射发掘隐含的非线性特征,并利用核技巧降低算法的时间复杂度。
2 RKANMF有向图聚类算法
本章讨论基于正则化核非对称非负矩阵分解(RKANMF)的有向图聚类算法。首先构造了新的聚类优化目标函数,给出参数优化方法;接着,提出优化该目标函数的聚类算法,并严格证明了算法的收敛性。
2.1 聚类目标函数及其优化方法
为在保持原空间中节点间(线性)相似关系的同时强化核空间中同簇节点间的(非线性)相似性,在构造约束核空间中节点相似性关系的正则项的基础上,利用核化机制定义RKANMF有向图核聚类目标函数如下:
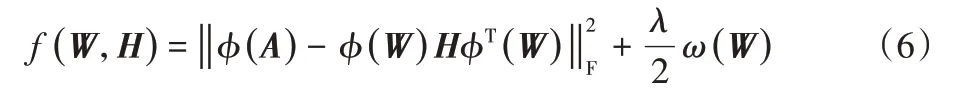
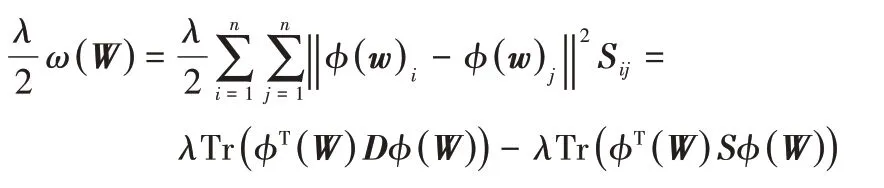
其中:D是对角线矩阵,其对角元Dii是矩阵S的第i行的和。整理聚类目标函数式(6)得到:

从优化角度分析,聚类是求解聚类目标函数最优值的过程,即在矩阵W和H非负约束条件下最小化式(7)。根据梯度下降方法,矩阵W和H通过迭代以下乘法更新规则求解:

其中Zd表示矩阵Z中每个元素的d次幂。
2.2 聚类算法及收敛性分析
依据2.1 节中W和H的更新公式(式(8)和(9)),提出基于RKANMF的有向图聚类算法,具体描述如下:
算法 基于RKANMF的有向图聚类算法。

计算KWAWd和KWWHKWW的时间复杂度分别为O(n2r)和O(r2(r+n)),由于r<n,每次迭代更新公式H的时间复杂度为O(n2r)。同理,每次迭代更新W的时间复杂度为O(n2r),因此,算法在不考虑迭代次数的情况下,时间复杂度为O(n2r)。
接着对算法的收敛性进行分析,借鉴文献[11,22]中的辅助函数法来证明在所提更新规则下算法的收敛性。
定理1式(7)中的目标函数在矩阵W和H的更新规则式(8)和(9)下是单调非增的。
证明 当固定H时,令
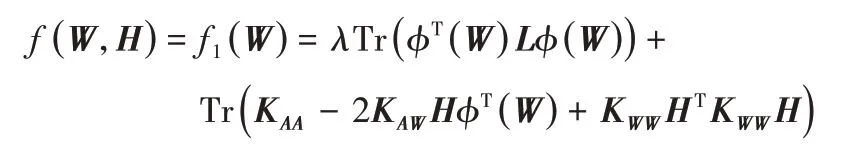
可得以下三个不等式:

令φ(W)=Wd,即得式(8)中W的更新公式。
同理,当W固定时,正则项部分与H无关。此时,令
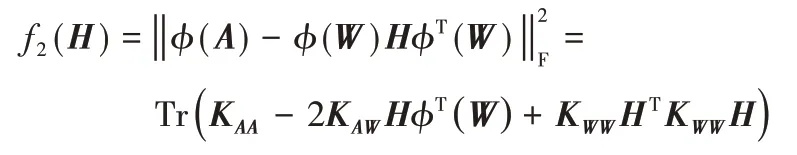
则有:
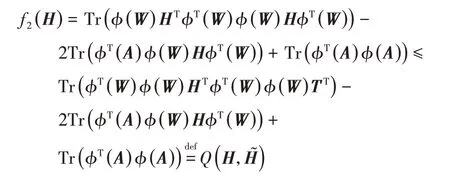

得出式(8)中H的乘法更新公式。又由于
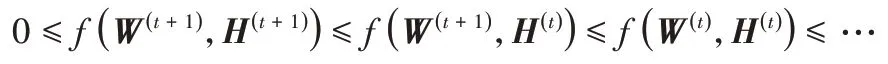
3 实验与分析
本章通过在三个领域有向网络数据集上的实验来验证所提算法RKANMF 在有向图聚类中的有效性,并与当前若干主流算法(ANMF[11]、RANMF[12]及DeepWalk 算法[13])进行对比。实验平台如下:Core i7-9750 2.60 GHz CPU,16.00 GB 内存,操作系统为Windows 10。
3.1 数据集
实验使用的有向网络数据集包含专利-引文网络(Patent Citation Network,PCN)数据集[23]、World Wide Knowledge Base(WebKB)数据集[24]和人工合成网络LFR(Lancichinetti-Fortunato-Radicchi)数据集[25],数据集的详细信息见表1。
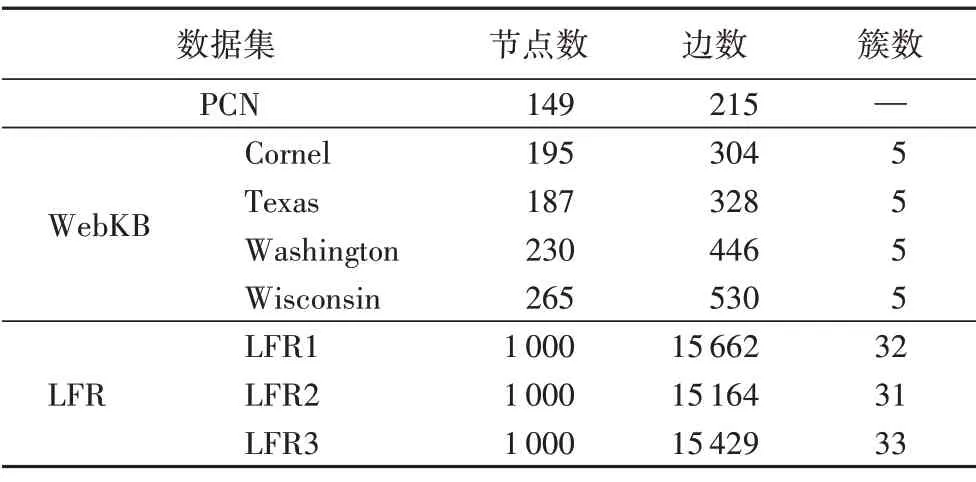
表1 有向网络数据集的详细信息Tab.1 Details of directed network datasets
①PCN 数据集。PCN 由4 142 个节点和18 385 条边组成,形成一个单一的连接树结构。本文选择PCN 中的149个节点(专利)和215 个有向边(引用)来检验聚类效果。由于同一簇的专利不一定具有直接公共邻居,而是具有一个或多个中间专利连接的非中间邻居,因此根据式(1)计算相似矩阵。由于PCN数据集没有提供节点标签,因此该数据集的簇数目未知,表1用“—”给予了标识。
②WebKB 数据集。该数据集包含从4 所大学(Cornel、Texas、Washington 和Wisconsin)收集的网页,网页分为学生、课程、项目、教师和工作人员5 类。通常,一个高质量的簇应具有较少的簇间连接和更多的簇内连接。由于WebKB 数据集中的簇与簇之间的连通性较高,选用式(2)计算节点间的相似矩阵。
③LFR 数据集。LFR 是一个人工合成数据集,包含的网络是根据某些参数控制的机制产生的。比如,通过混合参数μ控制合成网络中簇间连通性的强度,其值越大意味着更强的簇间连通性。本文取μ=0.1,0.3,0.5(分别对应表1 中的LFR1、LFR2 和LFR3),并使用Katz 中心相似性度量式(2)计算节点间的相似矩阵。
3.2 评价指标
当数据集没有真实簇划分时采用Davies-Bouldin(DB)指标[26]和Distance-based Quality Function(DQF)指标[27]评价多个算法的聚类结果质量;当存在真实簇划分时采用聚类准确率(ACcuracy,AC)指标、NMI 指标及Jaccard 指标[28]。各指标简要介绍如下:
①DB指标。
计算簇内散射与簇间分离之比,公式如下:
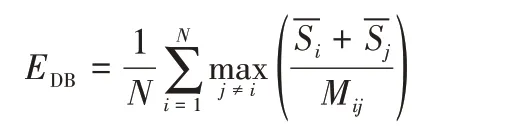
其中:N表示簇的个数;表示第i个簇中节点的平均分散程度;Mij为第i类与第j类簇的距离。当DB 指标值越小时,算法得到的聚类效果越好。
②DQF指标。
计算簇与簇之间的平均距离,公式如下:
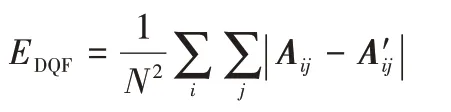
其中:A表示邻接矩阵;是根据算法得到节点簇集合划分r个簇后构建的新邻接矩阵,若节点i与j同簇,则。DQF指标越高,则得到的聚类结果越好。
③AC指标。
计算预测的节点簇集合的准确率,公式如下:
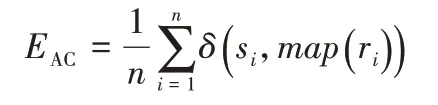
其中:n表示节点个数;ri、si分别为第i个节点所对应的获得的标签和真实标签;map(ri)是一个映射函数,表示将ri映射到相应的节点簇类上。δ是指示函数,其公式如下:

AC指标越高,聚类质量越高。
④NMI指标。
计算预测的节点簇集合与真实节点簇划分的相似度,公式如下:
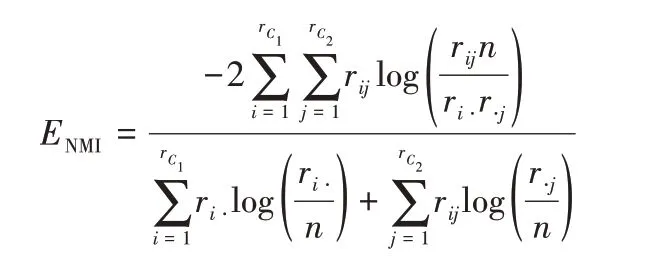
其中:C1和C2分别是预测的节点簇集合与真实节点簇集合;分别表示真实簇的数目与预测簇的数目;矩阵R=代表混淆矩阵,rij为真实簇的节点i出现在发现簇j的数量,ri⋅和r⋅j分别是混淆矩阵第i行的和与第j列的和。NMI指标越高则聚类质量越好。
⑤Jaccard指标。
计算预测的节点簇集合与真实节点簇集合的交集和并集之比,公式如下:

其中:C1表示预测的节点簇集合,C2为真实节点簇集合。Jaccard指标越高,则得到聚类结果与真实簇划分越相似。
3.3 参数设置
为检验本文RKANMF 算法是否能有效建模节点间的非线性关系,将它与ANMF算法[11]、RANMF算法[12]进行了比较,并通过对比DeepWalk算法[13],检验了小样本条件下算法对有向聚类的准确性。
在对不同网络数据集的实验中,RANMF 算法与ANMF 算法中Katz 中心相似性度量的β参数以及惩罚项权重系数λ的设置与文献[12]中的最佳参数一致,所有基于NMF 的算法统一设置迭代停止精度ε=10-6。DeepWalk 算法参照文献[13]设置每个节点出发游走10 次,游走长度为10;skip-gram 模型设置词向量的维度为30,窗口大小设置为7。
簇的数目r值是有向图聚类算法的重要问题,也是各个算法需要设置的先验参数,本文在具有类标签的数据集上采用真实簇的数目作为r值,对于没有类标签的PCN 数据集,选取不同的r值来对算法性能进行测试。
在真实网络数据集中(PCN 和WebKB 数据集)重点讨论分数阶核的次幂d值与惩罚项权重系数λ值对RKANMF 算法的影响。在PCN 数据集的实验中,为了与ANMF 与RANMF算法进行对照实验,RKANMF 算法设置共同的参数λ=0.1,β=0.2。当参数d值取得过小时,计算过程中,W的更新公式(8)中的分母可能会接近于0,因此选择d值在0.2 到0.9 区间。图1与图2显示当簇数r=2,d=0.2时,RKANMF 算法在DB与DQF指标上均取得最优。随着d值增加,越趋近于1时,算法不再对节点间的非线性关系建模,从而导致聚类质量下降。为检验簇数不同时对算法的影响,统一设置参数d=0.2。
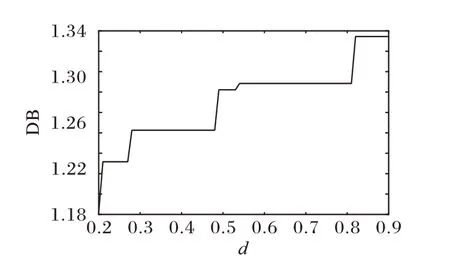
图1 参数d对DB指标的影响Fig.1 Influence of parameter d on DB index
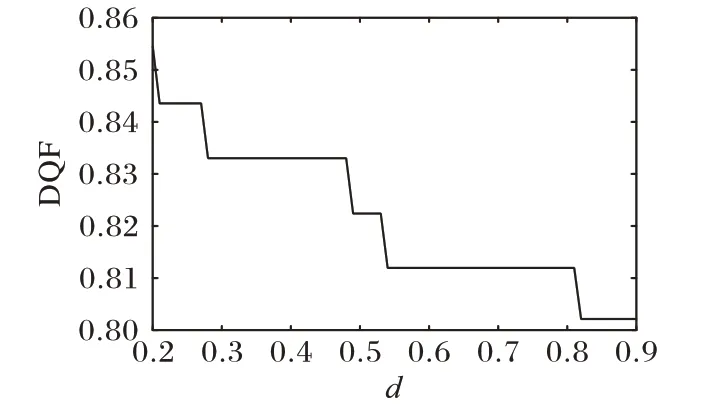
图2 参数d对DQF指标的影响Fig.2 Influence of parameter d on DQF index
在具有真实簇划分的WebKB 数据集实验中,着重考虑d值在0.2 到0.9 区间变化时,RKANMF 算法对AC 指标的影响。结果如图3所示,在多个子数据集上,当d值在0.4到0.5之间时,算法的聚类结果在AC 指标上更高。当d值趋于1 时AC指标呈下降趋势,算法不再建模节点间的非线性关系从而导致聚类质量下降。根据图3,对四个子数据集(Cornel、Texas、Washington 和Wisconsin)分别取合适的d值为0.4、0.4、0.9和0.5。
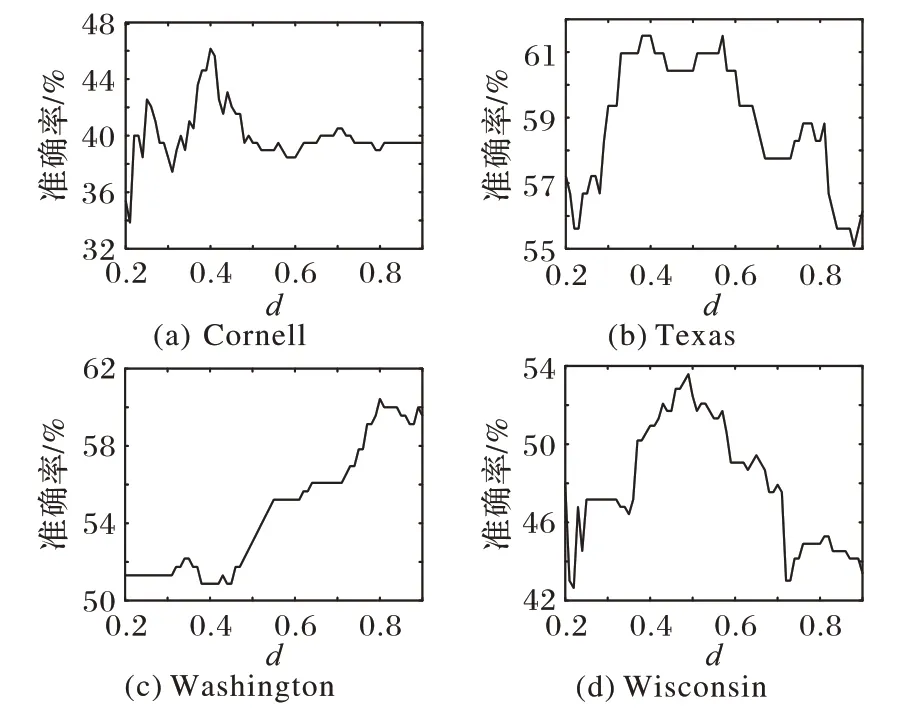
图3 WebKB数据集上d值对AC指标影响Fig.3 Influence of d value on AC index on WebKB dataset
为考虑λ值对算法的影响,当固定d值后,设置权重系数λ值区间为0 到500。图4 显示,当λ值越大时,算法越倾向于考虑节点间的相似性信息;当λ值过大时,算法过于依赖节点相似性,将原来属于不同簇的节点划分到同一簇中从而导致聚类准确性下降。根据图4,对四个子数据集(Cornel、Texas、Washington 和Wisconsin)分别取合适的λ值为20、5、50 和20。同理,在LFR 的3个数据集中,所提算法通过对比多次得到的AC指标值,设置合适的参数β=0.1,λ=0.1,d=0.88。
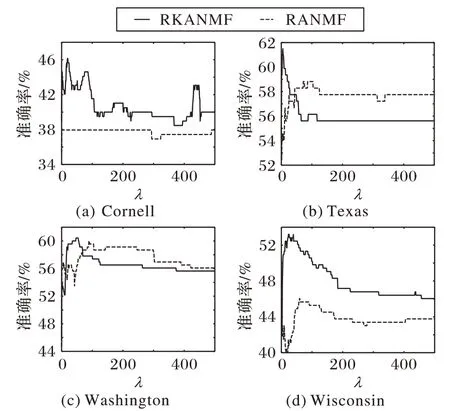
图4 WebKB数据集中λ值对AC指标影响Fig.4 Influence of λ value on AC index on WebKB dataset
3.4 PCN数据集的实验结果对比分析
本节使用PCN 数据集[23]来检验四种算法的性能表现。表2 是利用DB 和DQF 指标上对不同算法进行比较的结果。方便起见,表中均采用“Rnd”对随机初始化策略进行标识;用“SVD”表示基于SVD策略[12]的初始化,方法与文献[12]一致;使用随机初始化策略的算法运行100 次,每一次都按不同的初始化矩阵进行迭代,取最终结果的平均值。
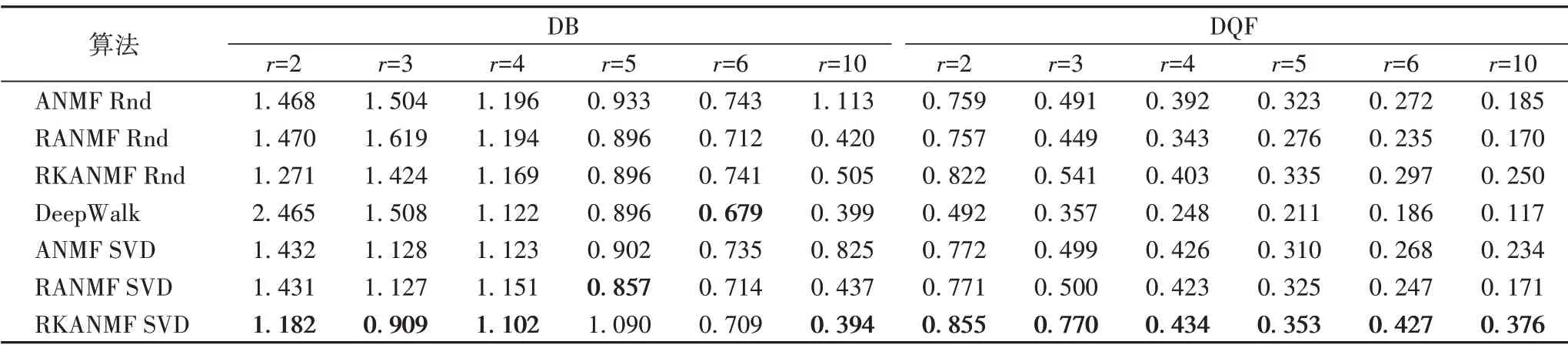
表2 簇数(r)不同时各算法在PCN上的DB和DQF指标比较Tab.2 Comparison of DB and DQF indexes on PCN for each algorithm with different number of clusters(r)
表2 结果表明,随着簇数r的增加,所有算法的聚类质量均有所下降,说明当簇的数目r越来越多时,本应该划分到相同簇的节点被分到不同簇,导致聚类质量降低。对于DB 指标,当簇数r=6 时,RANMF 算法与RKANMF 算法的DB 指标均低于DeepWalk 算法,这是由于过多考虑非中间邻居从而导致聚类效果变差。对于DQF 指标,在随机初始化的情况下,所提算法也能比基于SVD 策略初始化[12]的RANMF 与ANMF算法在DQF 指标上取得更好的表现。这说明RKANMF 算法有效地对节点间的非线性关系建模得到了更好的特征表示,显著提高了聚类质量。对比三种基于NMF 的算法可知,好的初始化策略及考虑了非线性关系的NMF 算法均能避免分解过程陷入较差的局部最优值。
3.5 WebKB数据集的实验结果对比分析
本节使用WebKB 数据集[24]中的四个子数据集来检验几种算法在数据集的簇间连通性强时的性能,结果如表3。可以看出,当数据集簇间连通性较高时,基于随机初始化策略的算法能得到较好的聚类结果,这是由于经过多次随机初始化的过程,算法更容易找到一个更好的局部极小值。对比基于NMF 的算法与DeepWalk 算法可知,在大多数情况下,基于NMF 的算法能得到更好的聚类结果。这说明当图的结构变得模糊,DeepWalk 算法无法准确获取有向图的高阶近邻结构,从而导致聚类质量下降。

表3 各算法在WebKB数据集上的结果比较Tab.3 Result comparison of different algorithms on WebKB dataset
在Cornell 子数据集中,RKANMF 算法在NMI 指标上最高,表明在数据集的簇间连通性高的情况下,RKANMF 算法也能有效发掘节点间非线性关系。在Texas 子数据集中,RANMF 与RKANMF 算法的NMI 指标低于ANMF 算法,因为在正则项权重系数逐渐变大的过程中,带正则项的两个算法均忽视了邻接矩阵的结构信息,从而聚类质量下降。
3.6 LFR网络数据集的实验结果对比分析
本节使用LFR网络[25]来检验几种算法检验在度分布不平衡的复杂网络中的表现,结果如表4。表4显示了不同算法在LFR 网络上的实验结果,其中“—”表示基于SVD 策略初始化的ANMF算法得不到聚类结果。由表4可以看出,随着μ值的增加,算法对簇的划分变得愈加困难。当簇类结构变得模糊时,基于NMF 的算法在NMI 指标上低于DeepWalk 算法,这说明DeepWalk 更有针对性地获取图的结构来提高划分簇的质量。RKANMF 算法在AC 和Jaccard 指标上有更好的表现,这是由于RKANMF 算法中正则项发掘了节点间的(非线性)相似性关系。相比其他基于NMF 的算法,RKANMF 不仅在NMI指标上与DeepWalk 算法比较接近,且在AC 和Jaccard 指标上有显著的提高,这说明当节点关系变得复杂时,对节点间的非线性关系进行建模能更有效地提高聚类算法的表现。
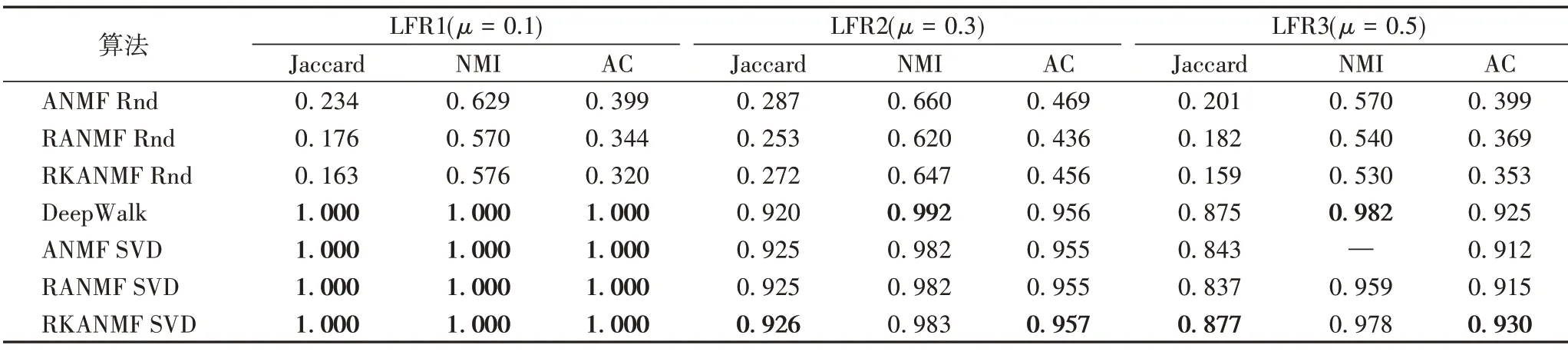
表4 各算法在LFR网络数据集上的结果比较Tab.4 Result comparison of different algorithms on LFR network dataset
4 结语
本文提出了一个用于有向图聚类的图正则化核非对称非负矩阵分解优化方法。该方法基于核化机制构造了有向图聚类新目标函数,其正则项同时考虑了原始空间中节点间的相似性及节点在核空间中的(非线性)相关性;基于梯度下降法推导了一个有向图聚类(RKANMF)算法,给出了算法的详细过程及收敛性分析,并在多个有向网络数据集进行了实验。实验结果表明,与未结合核学习方法的非负矩阵分解算法及DeepWalk 等算法相比,新算法在多个聚类有效性指标上有更好的表现。今后我们将针对性地考虑节点的方向性以及不同核函数对有向图聚类的影响等方面做进一步研究。
