基于空间收缩技术的约束多目标进化算法
2022-01-05李二超毛玉燕
李二超,毛玉燕
(兰州理工大学电气工程与信息工程学院,兰州 730050)
(∗通信作者电子邮箱lecstarr@163.com)
0 引言
多目标优化问题(Multi-objective Optimization Problem,MOP)在实际科研和工程实践中应用非常广泛,然而许多实际问题往往伴随各种各样约束条件的限制[1],这些约束条件导致搜索空间的拓扑结构变得十分复杂,如可行域狭小、存在多个不连通可行域等。例如,环境经济电力调度[2]、机器人抓手优化[3]等。这类带约束条件的多目标优化问题统称为约束多目标优化问题(Constrained Multi-objective Optimization Problem,CMOP)。不同于MOP,求解CMOP 对目标函数优化的同时还需要满足约束条件,而优越的无约束进化算法在求解约束优化问题时一筹莫展,因此,对约束多目标进化算法(Constrained Multi-objective Evolutionary Algorithm,CMOEA)的研究具有非常重要的理论价值和实际意义
约束优化进化算法中,根据处理约束方法的不同可以将约束处理机制大致分为六类:罚函数法、可行性准则、随机排序法、ε约束处理法[4]、多目标优化法和混合法[1]。CMOEA 根据进化算法中保留解的方式可以分为基于支配和基于分解两类。基于支配的算法如C-NSGA-Ⅲ[5]、NSGA-Ⅱ-CDP[6]等。基于分解的算法如C-MOEA/D[7]、MOEA/D-Epsilon[8]、MOEA/DCDP[9]等。上述算法均过分强调可行解,忽略了不可行解携带的信息。为克服此缺点,平衡CMOEA 收敛性、多样性和可行性,两阶段、多存档集的进化算法开始用于求解CMOP。Liu等[10]提出了针对目标函数和决策空间约束的两阶段搜索算法ToP;Li 等[11]提出了双归档集进化算法C-TAEA(Two-Archive Evolutionary Algorithm for Constrained multi-objective optimization);Cai 等[12]提出两 阶段算法PPS(Push and Pull Search)用于求解不可行域较大问题,第一阶段不考虑约束条件得到无约束Pareto 前沿,第二阶段考虑约束条件和目标函数将无约束Pareto 前沿拉至约束Pareto 前沿。上述算法在处理约束优化问题中均取得了显著的成果,但在不可行域较大时,对不可行域的搜索过多或过少都会引起算法性能下降。上述算法在追求对不可行域充分探索的同时,增加了对无潜力不可行域的搜索,使算法效率降低且收敛精度不高。
对于不可行域较大的约束优化问题,为减少对无潜力不可行域的搜索,提高算法收敛性、多样性和可行性的平衡能力,本文在PPS 算法基础上提出一种混合约束处理技术,将ε约束处理法与空间收缩技术相结合,在进化过程中调整决策变量上下限,减少无潜力不可行域的影响。
1 相关概念
1.1 约束优化问题定义
以最小化问题为例,约束多目标优化问题可定义为如下形式:

其中:x=(x1,x2,…,xD)∈Ω是包含D个决策变量的解,Ω∈RD是决策空间;F:Ω→RM由M个目标函数组成;gj(x)为q个不等式约束,hj(x)为m-q个等式约束。
在约束优化问题中,通常将等式约束转化为不等式约束,因此,个体x在每个约束条件上的约束违反程度为:
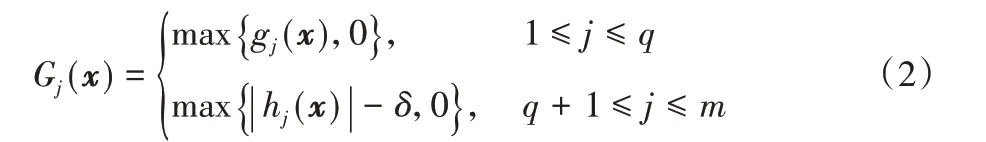
其中δ为等式约束的容忍参数,个体x总约束违反度为:

1.2 ε约束处理法
ε约束处理法通过设定ε值,根据个体总约束违反度将个体划分到不同的区域,不同区域内的个体采用不同的评价标准。该方法使用分段函数来控制ε,根据式(6)评价个体的优劣:

其中:k为当前代数,Tc为控制代数,cp控制ε减小速率,ε(0)的定义如式(5)。

其中:xθ为种群中个体按约束违反度升序排序后第0.05N个个体。

其中:v1、v2表示两个解的约束违反度,f1、f2表示两个解的目标函数值,公式的前两行表示当两个解的约束违反度都小于ε或者两个解约束违反度值大于ε但相等时,根据目标函数值选择目标函数值更小的解;其他情况,即两个解约束违反度值有一个或者两个都大于等于ε 且不相等时,根据约束违反度值选择约束违反度更小的解。
2 本文算法
本文提出的基于空间收缩技术的约束多目标优化算法(Constrained Multi-Objective Evolutionary Algorithm based on Space Shrinking Technique,CMOEA-SST)首先对PPS 中两阶段的过渡种群进行改进,提出自适应精英保留策略;然后在PPS 算法第二阶段加入空间收缩技术,对决策变量的上下限进行调整,缩小搜索空间,减少对无潜力不可行的搜索。
PPS算法在第一阶段得到无约束Pareto前沿,在第二阶段则将无约束Pareto 前沿进一步进化到有约束Pareto 前沿。这种搜索机制虽然能够快速跨越不可行域,但是对于无约束Pareto 前沿和有约束Pareto 前沿分离的优化问题(如图1 所示),Push 阶段结束时种群为无约束Pareto 前沿,由图1 可知,此时种群中并不含有约束Pareto前沿上的任何解,种群的收敛性和可行性较差。因此,本文提出精英保留策略,保留Push阶段进化过程中的高质量解,并在Push阶段完成时,自适应替换种群中部分解。自适应精英保留策略能够增加求解有无约束Pareto 前沿分离问题时Pull 阶段初始种群的多样性和可行性。
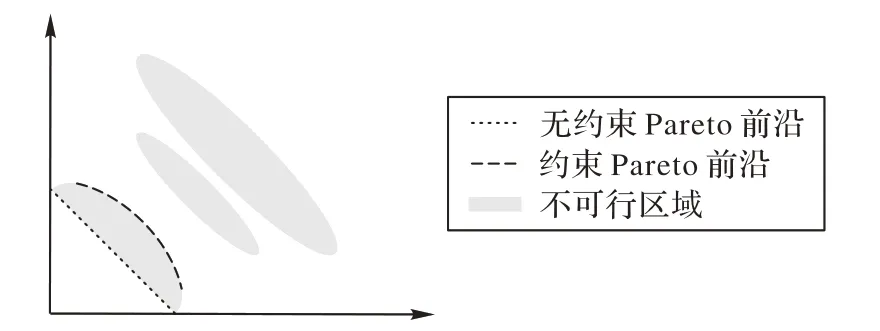
图1 有无约束的Pareto前沿分离示意图Fig.1 Schematic diagram of unconstrained and constrained Pareto front separation
对于不可行域较大的问题,很难得到可行解,需要充分利用不可行解的信息。而对于众多不可行解,部分解对求解Pareto 最优解集有利,部分解对寻找Pareto 最优解并无任何帮助,此部分解所在区域成为无潜力不可行域。而过度增加对无潜力不可行域的探索会降低算法性能,因此需要合理对不可行域进行搜索。为此,本文在PPS 算法第二阶段提出混合约束处理技术,在改进ε约束处理技术基础上增加空间收缩技术。改进ε约束处理技术能够利用不可行解的信息,空间收缩技术则对决策变量上下限进行调整,随着时间的推移,搜索空间逐渐减小。所提混合约束处理技术能使算法在对不可行域充分探索的同时减少无潜力不可行域对算法性能的影响,能够有效提升算法的收敛性能。
2.1 MOEA-SST
算法1 描述了本文算法CMOEA-SST 的主要框架,其中第3)~6)行为初始化参数,包括初始种群、参考点、搜索状态及其他参数;第8)行执行Push 阶段精英保留策略,将精英个体保存在Xsst中;第9)行计算l代进化以来理想点和最差点的最大变化率,其中理想点和最差点的变化率根据式(7)、(8)求取;第11)~19)行判断搜索过程是否切换,当最大变化率小于φ(φ取0.001)且搜索过程为Push 阶段时,搜索过程进行切换,并判断是否应该启动精英保留策略,其中第14)~17)行执行精英保留策略;第21)行更新ε值,采用改进的ε约束处理法,更新方法如式(9)所示,满足前期搜索过程中ε迅速减小,使得种群快速穿越不可行域,后期ε减小率降低,可以更彻底地搜索可行解;第28)~30)行采用差分进化操作[13]生成一个新解,并对该解进行修复改进;第34)~41)行更新邻域,根据两阶段搜索过程不同,Push阶段以聚合函数值gte(x|λ,z*)=为判断依据,选择gte小的解,Pull 阶段则根据gte、v(x)、ε(k)(ε约束处理法)选择个体;第42)~44)行为空间收缩技术,具体流程如算法3 所示;第45)行更新迭代次数;第46)行根据个体的非支配等级和拥挤度距离更新可行的非支配解集合NS。
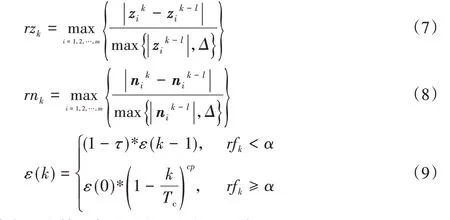
其中rfk为第k代种群中可行解的比例。
算法1 CMOEA-SST的一般框架。


2.2 自适应精英保留策略
PPS 算法两阶段搜索过程虽然能够充分探索不可行域,但当优化问题的无约束Pareto和约束Pareto前沿分离时,第二阶段初始种群中不包含可行解,并且随着有无约束Pareto 前沿的距离越大,第二阶段初始种群表现出的可行性越差。因此,本文采用自适应精英保留策略对PPS 两阶段的过渡种群进行改进,以提升算法Pull阶段初始种群的多样性和可行性。
自适应精英保留策略主要思想:在Push 阶段保留约束违反度小于ε(0)的非支配保存,当Push阶段完成时,以当前种群中可行解比例作为启动精英保留策略的依据,当可行解比例小于0.5时,随机剔除种群中N/6个体,并按约束违反度从小到大的原则选择N/6个精英解进行补充。具体过程如算法2所示。
算法2 保留Push阶段精英个体。

2.3 空间收缩技术
空间搜索技术是反向收缩帕累托存档进化策略(Inverted-Shrinkable Pareto Archived Evolution Strategy,ISPAES)[14]的重要组成部分,在进化过程中,利用可行域周围个体所携带的全局信息将搜索精力集中在更小的搜索空间上。
空间收缩技术每隔Ts代执行一次,具体过程实现如下:
1)选择0.15N个最佳个体。针对每一个约束条件,从种群中删除该约束条件最差的个体,直至所剩个体数量为0.15N。
2)求取决策变量最值。从所选的最佳个体集合中求取每一个决策变量的最大最小值。
3)根据当前种群中最佳个体决策变量的最值对搜索空间进行缩小,决定新的决策变量上下限。每一个决策变量的搜索区间必须比之前决策变量的搜索区间减小(1-0.9(1/n))%。更多关于空间收缩技术的细节参考文献[14]。
本文将空间收缩技术嵌入Pull 阶段,用于平衡搜索过程中对可行域和不可行域的探索,减少对无潜力不可行域的搜索,能在平衡算法收敛性和多样性的同时有效提升算法的收敛性能。具体过程如算法3所示。
算法3 搜索空间收缩。

3 实验仿真与分析
3.1 测试函数与评价指标
为测试CMOEA-SST 的性能,选择LIRCMOP 系列测试问题,根据文献[4]将LIRCMOP 系列测试函数的信息总结为表1。为了测试不同算法性能,选择世代距离(Generational Distance,GD)和超体积(Hypervolume,HV)作为评价指标。其中:GD为收敛性评价指标,GD值越小表示所求解集与真实前沿越接近,算法的收敛性越好;HV 为综合性评价指标,HV值越大,算法的综合性能越好。
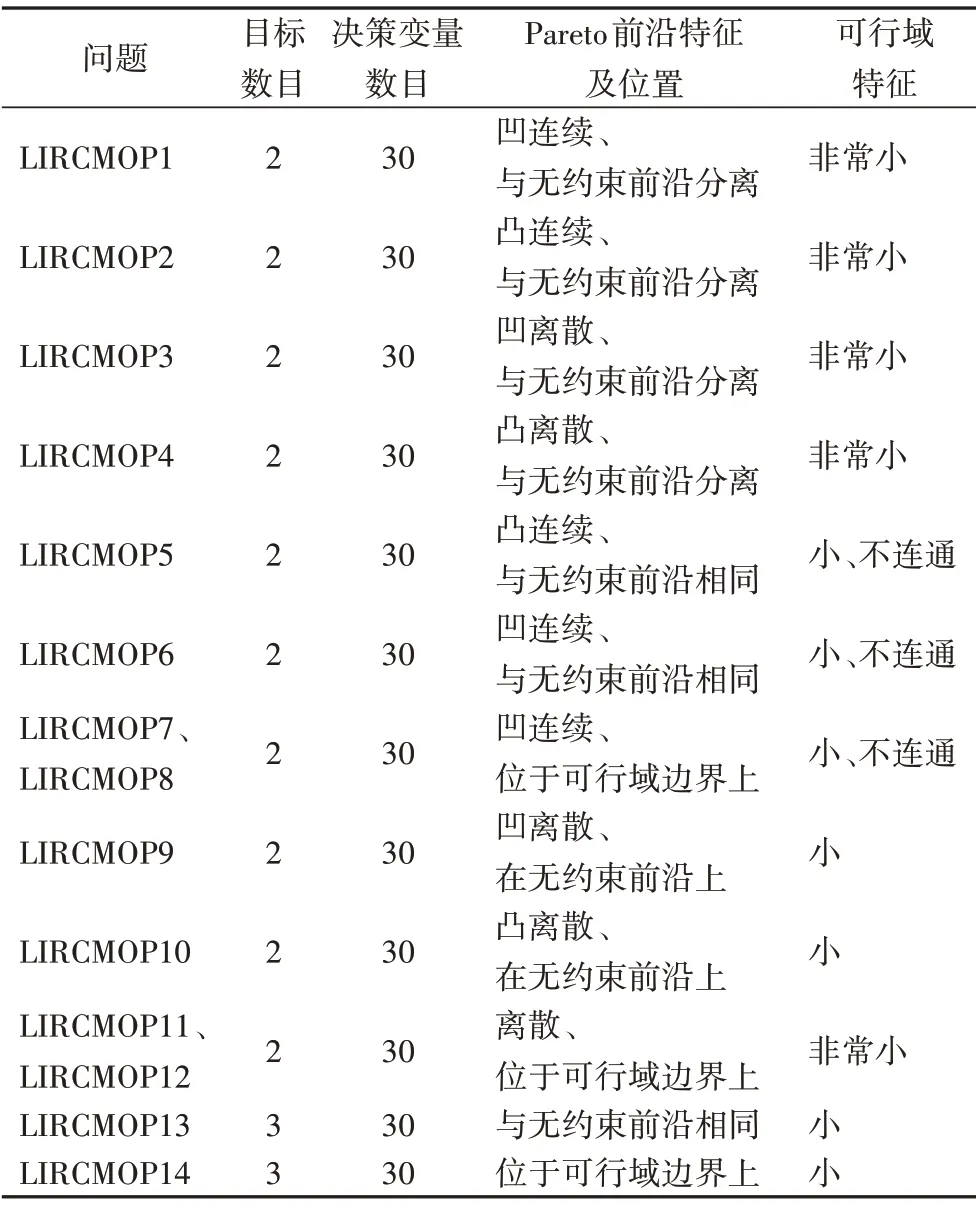
表1 LIRCMOP系列测试函数信息Tab.1 Information of LIRCMOP series test functions
3.2 实验配置与参数设置
实验环境为Matlab2014b版本,实验操作平台为开源平台PlatEMO[15]。实验参数设置如下:
1)变异概率Pm=1/n(n为决策变量的维数);多项式变异分布指标为20。
2)差分进化参数:CR=1,f=0.5。
3)种群大小:N=300,T=30。
4)终止条件:每个算法独立运行20 次,评价次数为300 000。
5)子代最大更新数目:nr=2。
6)PPS 参数设置与原论文保持一致:Tc=800,α=0.95,τ=0.1,cp=2,l=20。
7)为保证比较的公平性,C-MOEA/D、C-TAEA、ToP 算法参数均与原论文一致。
8)空间收缩技术参数:为合理设置收缩间隔Ts,将Ts分别设为30、40、50,并将独立运行20次的平均结果进行对比。设置不同Ts的算法在LIRCMOP2、LIRCMOP6、LIRCMOP8、LIRCMOP10、LIRCMOP12、LIRCMOP14 上的HV 值如表2 所示。从表2 可以看出,当Ts为40 时,所得Pareto 解集在LIRCMOP2、LIRCMOP5、LIRCMOP8、LIRCMOP12、LIRCMOP14 上的HV 值均最好。因此,为了保持种群良好的性能,Ts设置为40。

表2 不同Ts的对比测试结果Tab.2 Comparison test results with different Ts
3.3 实验结果与分析
3.3.1 算法有效性验证
为验证本文中混合约束处理技术的有效性,将PPS 算法与采用混合约束处理技术的PPS 算法(记为PPS-s)进行比较。表3 展示了PPS 与PPS-s 在LIRCMOP 测试问题上的GD 值,结果显示混合约束处理技术使得原始算法收敛性显著提升。
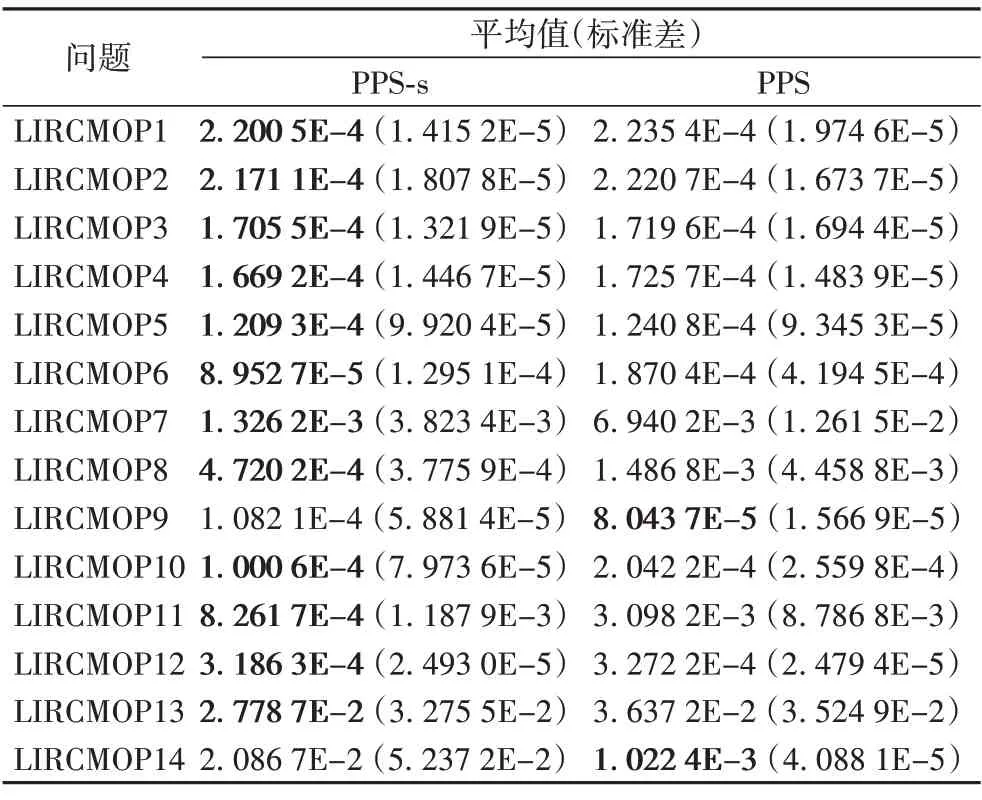
表3 两个算法在LIRCMOP系列测试函数上GD的平均值和标准差Tab.3 Average value and standard deviation of GD for two algorithms on LIRCMOP series test functions
3.3.2 算法性能验证
为验证所提算法的性能,选择C-MOEA/D[7]、ToP[10]、CTAEA[11]、PPS[12]四个流行的约束多目标优化算法进行对比研究。C-MOEA/D、ToP、C-TAEA、PPS 和CMOEA-SST 在14 个LIRCMOP 测试函数上独立运行20 次的GD 和HV 指标平均值和标准差如表4、5所示。
对表4分析可得,CMOEA-SST 在LIRCMOP1~LIRCMOP 5、LIRCMOP7、LIRCMOP8、LIRCMOP11、LIRCMOP12共9个测试函数上所得结果明显优于对比算法,说明CMOEA-SST表现出较好的收敛性。对表5 分析可得,CMOEA-SST 在LIRCMOP2、LIRCMOP5~LIRCMOP12 共9 个测试问题上表现良好。综合而言,CMOEA-SST 在求解不可行域较大问题上具有显著的优越性。
具体分析如下:
LIRCMOP1~LIRCMOP4测试问题在整个搜索空间中可行域极小并且有约束Pareto 前沿和无约束Pareto 前沿分离,由GD 指标可得,CMOEA-SST 在求解此类问题时表现出较好的收敛性,主要原因是空间收缩技术能够不断缩小搜索空间,继而增加Pareto前沿附近区域的搜索,使得所有Pareto最优解更接近于真实前沿。但是对于离散的LIRCMOP 问题而言,CMOEA-SST 的综合指标比PPS 差。图2、3 显示了在LIRCMOP1 和LIRCMOP3 上运行20 次后的平均结果:LIRCMOP1 问题上,C-MOEA/D、ToP、C-TAEA 没有得到Pareto前沿,CMOEA-SST 所得解集分布情况比PPS 要好;LIRCMOP3问题上,C-TAEA 完全没有接近真实Pareto 前沿,ToP 和CMOEA/D 只求得Pareto 前沿的一部分,CMOEA-SST 和PPS 所得解集的分布不均匀,还需进一步研究。

图2 各算法在LIRCMOP1测试函数上的仿真结果Fig.2 Simulation results of each algorithm on LIRCMOP1 test function
LIRCMOP5~LIRCMOP12测试问题具有较大不可行域,由表5 可知,所提算法在这8 个测试问题上综合指标优于其余4个算法,由表4 可得CMOEA-SST 在LIRCMOP5、LIRCMOP7、LIRCMOP8、LIRCMOP11、LIRCMOP12 共5 个测试问题上取得了较好的收敛性。LIRCMOP6 有无约束的前沿相同、LIRCMOP9、LIRCMOP10 约束Pareto 前沿为无约束前沿的一部分,本文采用的精英保留策略在求解此类问题时,能够增加Pull阶段初始种群的多样性,因此表现出优越的综合性能,同时作为代价Pull阶段原初始种群中部分收敛性能优良解被替换,会相应降低算法的收敛性。从表4 可得,CMOEA-SST 在LIRCMOP6 和LIRCMOP9、LIRCMOP10 问题上收敛性虽然优于前三个对比算法,却略差于原PPS算法,仿真结果与理论分析一致。对于三目标的问题LIRCMOP13、LIRCMOP14,本文算法表现较差。图4、5 展示了LIRCMOP9 和LIRCMOP12 的运行结果,由图可知,仅有CMOEA-SST 能够在两个问题上求得Pareto前沿,其余算法只能获得Pareto前沿的一部分或者完全没有接近真实前沿。

图3 各算法在LIRCMOP3测试函数上的仿真结果Fig.3 Simulation results of each algorithm on LIRCMOP3 test function

图4 各算法在LIRCMOP9测试函数上的仿真结果Fig.4 Simulation results of each algorithm on LIRCMOP9 test function

表4 五个算法在LIRCMOP系列测试函数上GD的平均值和标准差Tab.4 Average value and standard deviation of GD for five algorithms on LIRCMOP series test functions

表5 五个算法在LIRCMOP系列测试函数上HV的平均值和标准差Tab.5 Average value and standard deviation of HV for five algorithms on LIRCMOP series test functions

续表

图5 各算法在LIRCMOP12测试函数上的仿真结果Fig.5 Simulation results of each algorithm on LIRCMOP12 test function
4 结语
本文针对不可行域较大约束优化问题的求解,为平衡算法的收敛性、分布性和可行性,合理探索不可行域,考虑PPS算法求解此类问题时对不可行域充分探索的优势,结合自适应精英保留策略和空间收缩技术提出一种基于空间收缩技术的约束多目标进化算法。该算法将进化算法分为两阶段,在Push 阶段不考虑约束条件得到无约束Pareto 前沿,Push 阶段完成时自适应启动精英保留策略,提高Pull 阶段初始种群的多样性和可行性。Pull 搜索阶段增加空间收缩技术,每隔40代对决策变量上下限进行调整,缩小搜索空间,减少无潜力不可行域对算法性能的影响。综合分析本文算法与其他4 个约束多目标算法在LIRCMOP 系列测试函数上的仿真结果可知,本文算法在不可行域较大问题上表现良好;但该算法在求解三目标问题时出现了性能退化问题,如何提高算法在三目标及高维多目标问题上的性能是我们接下来的工作。
