高动态电动伺服系统多模复合控制技术*

马 睿，张新华，王 贯，王天乙，宋志翌

(北京自动化控制设备研究所·北京·100074)

0 引 言

新一代高超声速武器装备具有飞行跨空域、宽速域的特点[1]，其对电动伺服系统的动态特性、稳态性能、抗干扰能力均提出了更高的要求。电动伺服系统作为精准制导武器与飞行器控制系统的重要组成部分，主要由伺服电机、传动机构、功率驱动等复杂部件组成[2]，承担着调整飞行姿态与飞行轨迹的作用。电动伺服系统具有强非线性、机电参数不确定性等特点，这直接限制了系统动态特性与伺服精度的提升。

先进控制算法是提高伺服系统性能的关键。传统的电动伺服系统控制多采用频域分析方法进行设计，文献[3-4]根据系统输入输出信号之间的误差动态调整控制器参数，以实现位置跟踪性能；但是，参数辨识更新速度慢，对快变扰动抑制的效果不理想。文献[5-7]分别采用了不同类型的PID控制算法，在一定程度上实现了伺服系统的高动态控制。文献[8]提出了以模糊控制和神经网络为代表的智能控制，此类算法需要精准的特征模型，不适用于实际应用。文献[9]利用滑模变结构控制算法处理不确定扰动，具有结构简单、运行速度快、无需在线调节参数等优点；但由于时间滞后或系统惯性等误差因素的存在，可能导致动态响应速度较慢[10]。在时间最优控制时刻输出最大控制量，不断从一个边界值切换到另一个边界值，在位移差-速差相平面可化简为二次抛物线[11]。文献[12-13]将最优控制切换轨线上下平移一定的速度误差量以减小超调与抖动,在误差较小时切换为线性控制，但没有考虑到线性控制带来的稳态误差。文献[14-15]全面分析了Bang-Bang控制在二阶系统中的适用范围，对其在电动伺服系统中的应用进行了详细分析,认为其在使用中需要对控制策略做出改进。在分析电动伺服系统特征模型的基础上，本文提出了一种将时间最优控制与滑模变结构控制进行结合的多模复合控制算法，详细阐述了时间最优控制算法与滑模变结构控制算法的设计方法及其适用区间，并采用基于电动伺服系统动力学模型仿真的手段进行了验证。

1 电动伺服系统的特征模型

电动伺服系统的特征模型如图1所示，在相同驱动电压控制输入下，所建特征模型在动态响应与稳态响应允许的误差范围内与动力学模型等价，特征模型具有响应性能近似动力学模型的优点，在分析伺服系统输出性能时可摆脱对传统复杂模型的高精度需求，且易于工程实现。通常将电动伺服系统控制器输入信号与输出闭环传递函数用二阶系统近似表示为

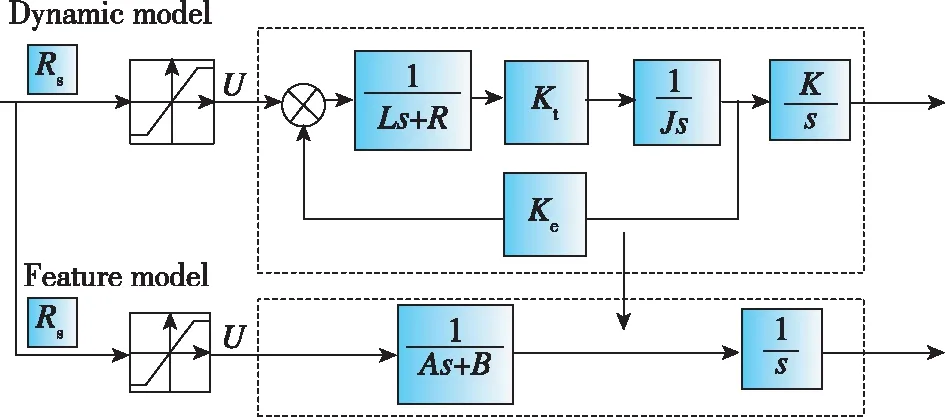
图1 电动伺服系统的特征模型

(1)

式(1)中，A、B为未知量，可根据特征模型输出。图1中，J为转动惯量；Kt为力矩系数；Ke为反电动势系数；U为额定电压；K为减速比；Rs为控制器输出信号；L和R分别为电机感抗与阻抗。针对电动伺服系统精准动力学模型建立从控制输出信号到伺服系统作动位置的传递函数

(2)

为方便研究，可忽略电机模型中的电气时间常数τe=L/R，同时对电动伺服系统进行特征建模。Rs到实际转速之间的传递函数简化为一阶惯性环节，实际转速到伺服系统位置的传递函数简化为一阶积分环节。根据图1，可将式(2)简化后的传递函数转化为微分形式

(3)

2 多模复合控制算法

2.1 时间最优控制设计

时间最优控制(Time Optimal Control, TOC)设计采用Bang-Bang控制，在切换时间上完成两个常值之间的跳变。因此，能在最短时间内接近系统误差切换阈值。根据图1，将电动伺服系统特征模型简化为惯性环节与积分环节，可得到基于电动伺服系统特征模型的目标方程与约束条件

开环传递函数为

(4)

简化传递函数为

(5)

目标方程为

(6)

约束条件为

(7)

其中，x1(t)与x2(t)分别表示系统位置误差与速度误差；tf为到达最终指令位置的时间;取u=Umax，即伺服过程以最大驱动电压控制输入。Vmax为电动伺服机构的最大转动速度，由式(4)、式(7)可得到基于电动伺服系统特征模型的最优减速轨线

(8)

根据式(8)，可得到理想最优减速轨线如图2所示。

图2 理想最优减速轨线

由于电动伺服系统的实际控制参数受采样时间、测量精度及受控对象模型不确定性的干扰，同时Bang-Bang控制需要精准的系统参数，实际工况环境复杂，仅靠最优控制虽能得到良好的动态性能，但是不能完全达到预期的控制性能。为防止在误差较小时可能发生的高频抖动，需在系统误差小于切换阈值时切换另一控制策略，以增加系统的稳态精度。

2.2 滑模变结构控制设计

滑模变结构控制(Sliding Mode Control，SMC)能迫使系统向规定状态轨迹靠近，在处理不确定扰动时具有良好的效果。当系统误差小于切换阈值时，切换为滑模变结构控制，加强系统抗扰能力，提高稳态精度。

其中，设计滑模面

(9)

其中，c为滑模面参数;e=θd-θ；θd为理想位置信号;θ为实际位置信号。采用指数趋近律

(10)

其中，ε与k为参考系数，可通过更改其数值调整系统趋近速度。

满足李雅普诺夫函数即可满足能进入滑模状态。其中，滑模面参数c与趋近率参数ε以及k可在仿真中进行调整。综合式(9)、式(10)，可得式(12)

(11)

(12)

综合式(3)～式(12)，可得到电动伺服系统的滑模变结构控制算法如式(13)所示

(13)

2.3 多模复合控制设计

图3 多模复合控制适用区间

(14)

(15)

将切换点d的状态(x1,x2)代入式(14)，得到次优轨线的输入量U0。

综上所述，状态点(x1,x2)在Ⅱ区域时，采用时间最优控制，控制量u(t)=-Umax，系统快速接近减速轨线；在Ⅲ区域时，采用滑模变结构控制，使系统状态以微小的误差快速向零状态收敛，并减小模态切换时产生的暂态分量。

3 系统仿真验证与分析

为验证本文所提出算法的有效性，分别在仿真实验中验证了在小位移阶跃输入和正弦输入情况下，电动伺服系统分别采用时间最优控制(TOC)、滑模变结构控制(SMC)、多模复合控制(TOC+SMC)三种控制算法的控制效果。仿真模型采用了电动伺服系统精准动力学模型，并充分考虑到了负载、噪声对伺服系统的影响。其中，TOC算法的参数设定为A=0.0168、B=120；SMC算法的系统参数设定为ε=0.98、c=100、k=1；控制算法切换阈值d=0.15。电动系统的参数如表1所示。

3.1 阶跃响应

为验证本文所提出控制算法的阶跃响应性能，输入5°位置阶跃信号，采用TOC、SMC、TOC+SMC三种控制算法。阶跃响应波形如图4所示。

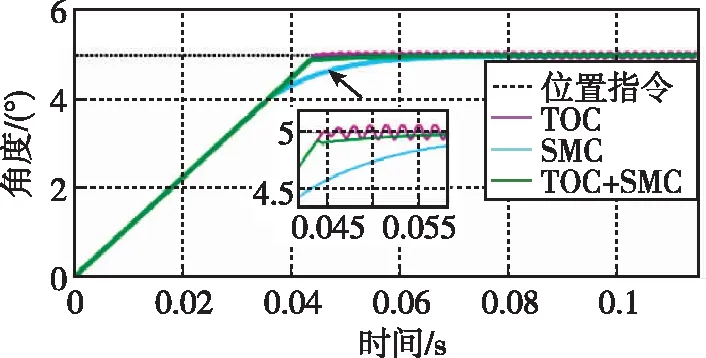
图4 5°空载阶跃响应仿真曲线

从图4可以看出，TOC的调节时间约为42ms，在三种控制算法中动态响应最快，但因无法准确切换，存在明显的超调现象与极限环，其振荡幅值约为0.1°；采用SMC算法时稳态性较好，无明显的振荡和超调现象，但调节时间为64ms，约为TOC算法的1.5倍;本文所提出的TOC+SMC多模复合控制算法的调节时间约为50ms，基本拥有与TOC算法相同的动态性能且不存在极限环。表2为对比空载下各种控制算法阶跃响应的性能指标。

表2 5°空载阶跃响应性能

为验证带载工况下本文所提出的控制算法的阶跃响应性能，在输入5°位置阶跃信号的同时加载10N·m/(°)的弹性负载，采用三种控制算法的响应波形如图5所示。

图5 5°带载阶跃响应仿真曲线

从图5可以看出，TOC算法的动态性能最好，调节时间约为52ms，但在带载工况下仍存在明显的超调与极限环；TOC+SMC算法的多模复合控制仍具有与TOC算法相似的动态性能和与SMC算法相同的稳态误差。表3为对比10N·m/(°)弹性负载工况下各种控制算法的阶跃响应性能指标。

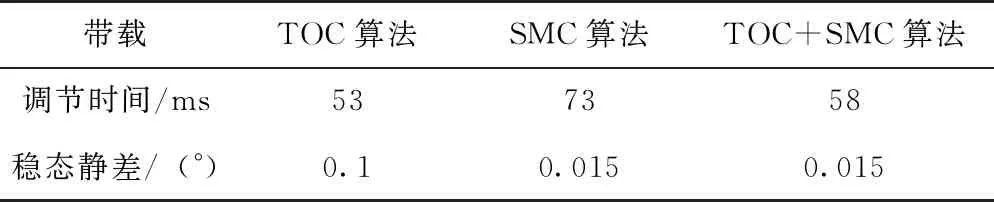
表3 5°带载阶跃响应性能

对比三种算法5°阶跃响应仿真结果，TOC算法的响应时间最短，但其在带载与空载情况下均出现了超调现象；SMC算法的控制调节时间最长，受扰动影响较小；TOC+SMC算法在5°阶跃指令及空载与带载工况下均具有与TOC算法接近的动态性能和与SMC算法相同的稳态静差。

3.2 正弦响应

为验证本文所提出控制算法的正弦响应的跟踪性能，输入幅值为5°、频率为5Hz的正弦扫频信号，在空载和弹性负载为10N·m/(°)时，分别采用TOC、SMC、TOC+SMC三种控制算法，得到跟踪响应波形分别如图6和图7所示。

图6 5Hz空载位置跟踪曲线

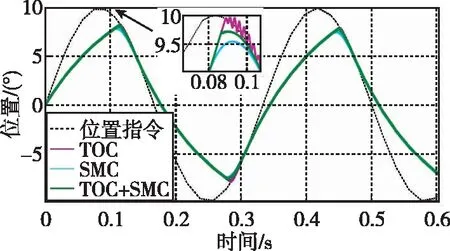
图7 5Hz带载位置跟踪曲线

由图6和图7可知，由电动伺服系统5Hz位置跟踪曲线可以看出：三种控制算法都有较强的跟踪性能并均在跟踪过程中出现了速度饱和现象。在空载状态下，TOC算法的跟踪误差较小，相位滞后约为9°，响应幅值为4.9°，但其跟踪速度存在不稳定性，并且在正弦峰值附近出现了抖动现象；SMC算法的相位滞后约为20°，响应幅值为4.7°；TOC+SMC复合控制算法的相位滞后为13°，约为SMC算法相位滞后的60%，响应幅值约为4.85°，整体性能更加优异。在弹性负载工况下，TOC算法的相位滞后为15°，响应幅值约为4.8°，同样在正弦信号峰值附近存在明显的抖动现象；SMC算法的相位滞后约为25°，响应幅值约为4.6°；TOC+SMC复合控制算法的相位滞后为18°，响应幅值约为4.85°，取得了很好的效果。

4 结 论

本文针对在电动伺服系统含有未知扰动情况下动态响应速度与稳态精度低的问题，先将电动伺服系统简化为特征模型，再通过设计时间最优控制算法与滑模变结构算法及其适用区间，使电动伺服系统具备高动态、抗干扰且无超调的稳定效果。在仿真中建立了TOC算法、SMC算法、TOC+SMC复合控制算法的仿真模型，对所提出的复合控制方案分别进行了阶跃和正弦跟踪的验证和分析。在负载工况阶跃响应中，TOC+SMC复合控制算法比SMC算法的调节时间少了15ms，且接近于TOC算法；在正弦跟踪中，TOC+SMC复合控制算法的相位滞后为SMC算法相位滞后的72%，且仅比TOC算法多3°。该多模复合控制算法基本同时具备SMC算法的稳态性能与TOC算法的动态性能，伺服系统的综合性能得到了提升，仿真结果验证了该理论分析的正确性与方案的可行性。