基于多矢量定姿的动基座最优化对准算法*
2022-01-05刘文倩程向红
刘文倩, 程向红, 曹 鹏, 丁 鹏
(1.东南大学 微惯性仪表与先进导航技术教育部重点实验室·南京·210096;2.东南大学 仪器科学与工程学院·南京·210096;3.上海航天控制技术研究所·上海·201109)
0 引 言
初始对准技术是捷联惯导系统的核心问题和关键技术。初始对准本质上是确定初始姿态矩阵的过程[1-6],包括粗对准阶段和精对准阶段[7-8]。粗对准是在短时间内提供一个大致已知的初始姿态矩阵,为精对准做好准备。代表性的粗对准方法主要包括静基座或准静基座下的解析法,以及动态环境下的基于优化的对准方法。解析法以地球自转角速度和重力加速度作为信息源[9]。虽然解析法原理简单,计算量小,但其仅利用了两个不同时刻的矢量观测信息,信息利用率不高,对准精度较低[8]。因此,可构建观测矢量组[10-14],将对准问题转化为多矢量定姿问题——即Wahba问题的求解。Wu和Pan等[10,15]采用最优对准(Optimization-Based Align-ment, OBA)方法提高了信息的利用率,从而提高了对准精度。但是,OBA方法的主要缺点是无法抵抗由陀螺偏置和随机噪声带来的影响。为了解决这些问题,Huang等[16]提出了一种新的快速运动粗对准方法(DAEBIA-FT)用于低成本的SINS/GPS系统。Chang等[17]将姿态对准问题转化成了姿态估计问题。但是,这些方法均需建立非线性状态空间模型,由此增加了计算难度。
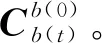
1 坐标系定义
常用坐标系的定义如下:
(1)地球坐标系(e系)—oexeyeze:地球坐标系的原点位于地心,oeze轴沿地球自转方向,oexe轴在赤道平面内,由地心指向载体所处子午线。e系与地球固联,随地球自转而转。
(2)导航坐标系(n系)—onxnynzn:导航坐标系的原点位于载体重心,onxn轴指向水平东向,onyn轴指向水平北向,onzn轴垂直于当地旋转椭球面并指向天。
(3)载体坐标系(b系)—obxbybzb:载体坐标系的原点位于载体重心,obxb轴指向载体横轴向右,obyb轴指向载体纵轴向前,obzb轴沿载体立轴向上。
(4)初始时刻载体惯性坐标系(b(0)系)—ob(0)xb(0)yb(0)zb(0):初始时刻将b系凝固后形成的坐标系。
(5)初始时刻导航惯性坐标系(n(0)系)—on(0)xn(0)yn(0)zn(0):初始时刻将n系凝固后形成的坐标系。
2 初始对准算法
传统双矢量定姿要求两个量测矢量具有极高的准确度,量测不准确会产生较大的对准误差。为克服该缺陷并提高对准精度,本文采用多矢量提供量测信息并进行对准,通过多个量测信息求解最优正交矩阵,将对准问题转化成了Wahba问题。
2.1 矢量信息的计算
(1)
(2)
(3)
(4)
进行分解可得
(5)
(6)
将式(6)左边定义为β,表示为
(7)

(8)
将β中的因式离散化求解如下
(9)
其中,T为姿态更新周期,k为更新次数,I表示单位矩阵。对α的离散化求解如下
(10)

(11)
2.2 Wahba 问题及SVD算法
(12)
其中,wi为权重系数,本文取为1。该式反映同一矢量在两个坐标系中测量值的不一致误差。
对式(12)中的误差平方进行如下的等价变形
(13)
将式(13)代入式(12),得
(14)
(15)
其中,αi、βi(i=1,2,…,m)表示b(0)系下观测矢量和n(0)系下观测矢量的第i个测量值。将式(15)中的矩阵A记为
(16)
假设矩阵A可逆且对其进行奇异值分解得到A=UDVT。其中,U和V都是酉矩阵,D表示由矩阵A的奇异值构成的对角矩阵,表示为D=diag(σ1,σ2,σ3),则式(15)可变为
=tr(C*D)
=max
(17)
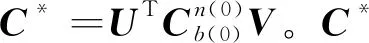
≤σ1+σ2+σ3
(18)

(19)
2.3 算法优化
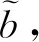
(20)
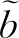
(21)
其中,φ×表示φ对应的反对称矩阵。将式(21)代入式(20)并变形,可得
(22)
根据姿态转换矩阵的微分方程,可得
(23)
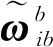
(24)
将式(22)代入式(23),忽略二阶小量,可得
(25)
令式(24)与式(25)相等,如下
(26)
经过简化整理,得到
(27)
文中,将陀螺零偏定义为常值,因此得到
(28)

(29)
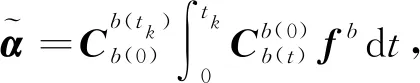
(30)
对式(30)进行整理移项,可得到量测模型
(31)
(32)
Zk=Hkφ
(33)
(34)
(35)
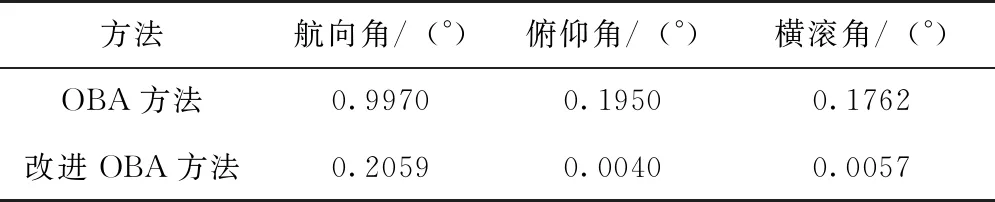
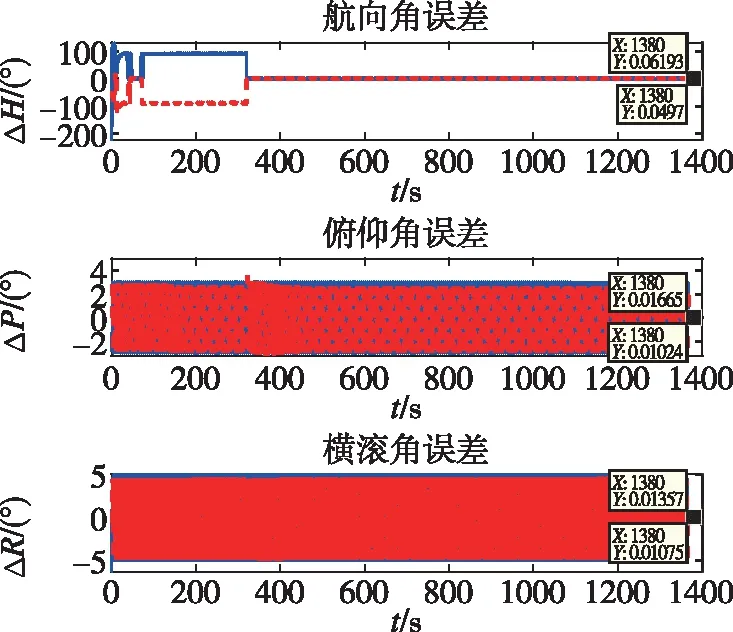
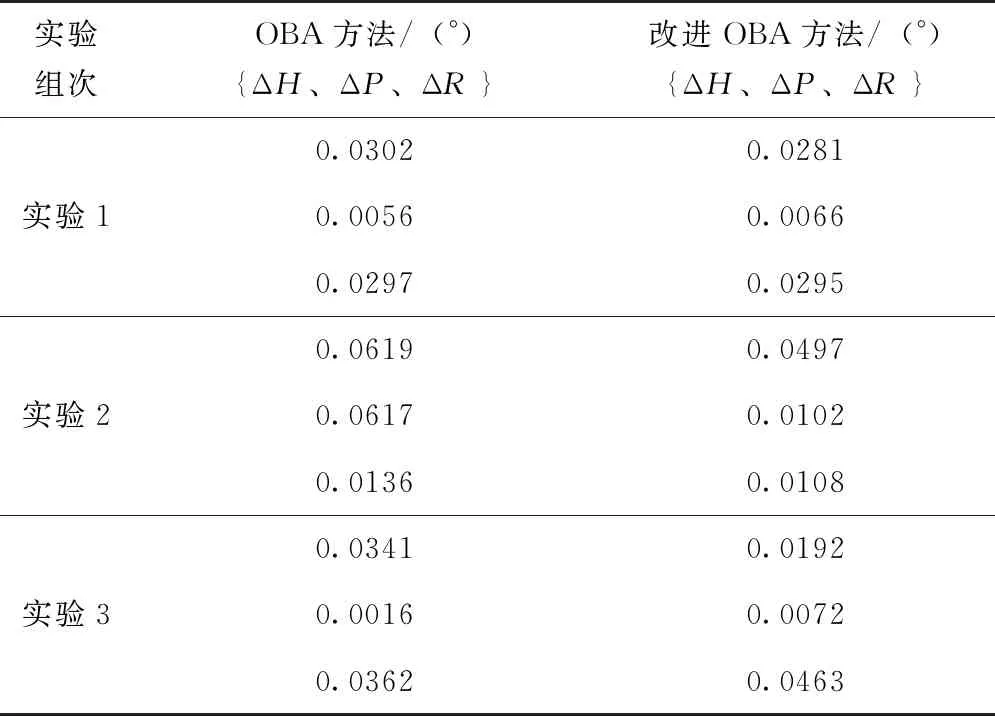
式中,Hk为k时刻的量测矩阵,Kk表示滤波增益,Pk表示状态估计的均方误差阵,ek表示新息。式中,dk=(1-b)/(1-bk+1),0 P(0)=diag{(0.01)2,(0.01)2,(0.01)2, (0.01)2,(0.01)2,(0.01)2} Q=diag{(0.01)2,(0.01)2,(0.01)2} R=diag{(0.1)2,(0.1)2,(0.1)2} 仿真中,载体首先进行60s的匀速运动,在60s~70s进行加速运动,加速度为0.1m/s2,在80s时进行拐弯运动,拐弯角度为40°,拐弯角速度为1(°)/s,并且伴有轻微的摇晃运动。航向角、俯仰角和横滚角摇晃幅度分别为1°、2°、3°,摇晃角频率分别为π/5(rad/s)、3π/10(rad/s)、2π/5(rad/s)。载体的运动轨迹如图1所示,行驶过程的总时长为420s,最大速度约为7m/s。 图1 仿真运动轨迹 图2 姿态角误差曲线 表1 350s~420s对准结果的均方根值(RMSs) 利用三轴转台进行3组微幅晃动条件下的对准实验。航向角H、俯仰角P、横滚角R的摇摆幅值和摇摆频率设置如表2所示。陀螺仪和加速度计的主要技术指标为:陀螺仪的常值漂移为0.01(°)/h,随机游走为0.005(°)/h1/2,加速度计的常值偏置为0.1mg,随机游走为0.1mg/Hz1/2。图3表示第二组数据在分别采用传统OBA方法和改进OBA对准方法时的对准曲线。 表2 摇摆条件设置 图3 姿态角误差曲线 表3 3组实验的对准结果3 仿真实验及分析
3.1 数学仿真实验
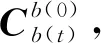

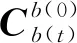

3.2 半物理仿真实验

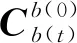
4 结 论