三次方阻尼和间隙变化下的冷轧垂直颤振研究

赵 武，张鸿斌，孙超凡，Motasim Masood，黄 丹

(1.河南理工大学 机械与动力工程学院，河南 焦作 454003；2.河南理工大学 材料科学与工程学院，河南 焦作 454003)

轧制装备的振动问题一直制约轧制产品质量的提高。随着科技进步和工业化发展，对轧件产品质量的要求也不断提高，研究轧机振动机理及其振动特性之间的转化机制就显得刻不容缓。轧制工艺过程中的振动现象，不仅会影响产品质量，甚至会造成生产事故。要求的轧薄能力越强，轧制精度越高，对轧制装备的振动控制越严格[1]。

目前，对轧机振动的研究主要集中在垂直振动[2]、水平振动[3]、扭转振动[4-5]以及不同方向的耦合振动。Tamiya等[6]建立了两自由度轧机振动模型，研究了张力及辊缝变化导致的振动对轧制的影响。Tlusty等[7]在Tamiya研究的基础上，深入探究后张力及接触弧长度动态变化对轧机振动的影响，结果表明：后张力的动态变化会引发带钢张力的相位延迟，与轧制力之间形成负阻尼机制，会导致轧机在垂直方向发生振动失稳。陈勇辉等[8]、Hu等[9-11]构建轧机振动模型及数值仿真，研究了冷轧机张力波动对三倍频垂直颤振的诱发过程；指出支承辊的振动以五倍频颤振为主，且在五倍频颤振产生之前系统已经因三倍频颤振而失稳。Roberts[12]认为上、下支承辊存在直径差并且支承辊周长为整数倍振动波长时，轧制系统易产生五倍频颤振，提出合理选择上、下支承辊直径以及改变轧制速度并抑制振动。

侯东晓等[13-14]研究了动态轧制力作用下的轧机垂振以及垂直-水平耦合的非线性振动中，阻尼与刚度对系统稳定性的影响。刘彬等[15]研究压下油缸的非线性刚度对轧机辊系垂振的影响，表明液压缸的非线性刚度越大，系统振动越不稳定。刘浩然等[16]考虑轧件的弹塑性变形引发的滞后非线性因素，构建垂直方向的非线性滞后振动模型，得到系统产生不同奇点的条件。孙韵韵等[17-20]研究了考虑轧辊表面形貌和粗糙度对辊系垂直非线性振动特性的影响。

文献[21-22]既研究了轧机非线性垂直颤振的幅频、主共振等特性，也研究了系统垂直参激振动对轧材成品厚度波动的影响机制[23-24]，获得了非线性振动系统在不同影响因素下的稳定参数的分布区域。

对轧机振动的研究模式，目前，一般分为两种思路：其一为对轧机工作过程的实际测试研究，通过对轧机振动监测数据的分析处理，来反映轧机的动特性和工作状态；其二为通过理论建模方式研究轧机的非线性振动，对轧制系统的分析主要依赖于模型；随研究的深入，目前的研究已发展为将监测数据进行分析处理后，与理论模型的仿真结果进行对照[25-27]。本文是基于理论建模的仿真和分析，通过分析冷轧垂直系统的颤振对薄板成型精度的干扰，探究该系统三次方阻尼和间隙变化下的垂直颤振机理及其演化机制；通过建立冷轧机在考虑三次方阻尼和间隙变化下的垂直颤振模型，运用数值计算方法，分析频率比、一次方刚度、一次方阻尼、三次方阻尼、偏心量以及间隙对冷轧垂直颤振系统分岔特性的影响，并利用双参平面的分岔图对系统在双参量变化下的运动特性进行解析，明确了系统发生混沌运动以及周期运动的状态转化规律，为冷轧工艺参数的规划设计及抑振减振提供了理论参考。

1 冷轧垂直颤振建模

1.1 冷轧垂直颤振的诱因分析

典型结构的四辊冷轧机如图1所示。图1中：Ⅰ和Ⅳ分别为上、下支承辊；Ⅱ和Ⅲ分别为上、下工作辊；Ⅴ为轧件；Ⅵ为机架。图1(a)中虚线为不考虑偏心时上、下工作辊的理论位置；图1(b)为上工作辊偏心放大图。上工作辊理论旋转中心为O1，实际旋转中心为O2，上工作辊偏心量为a。

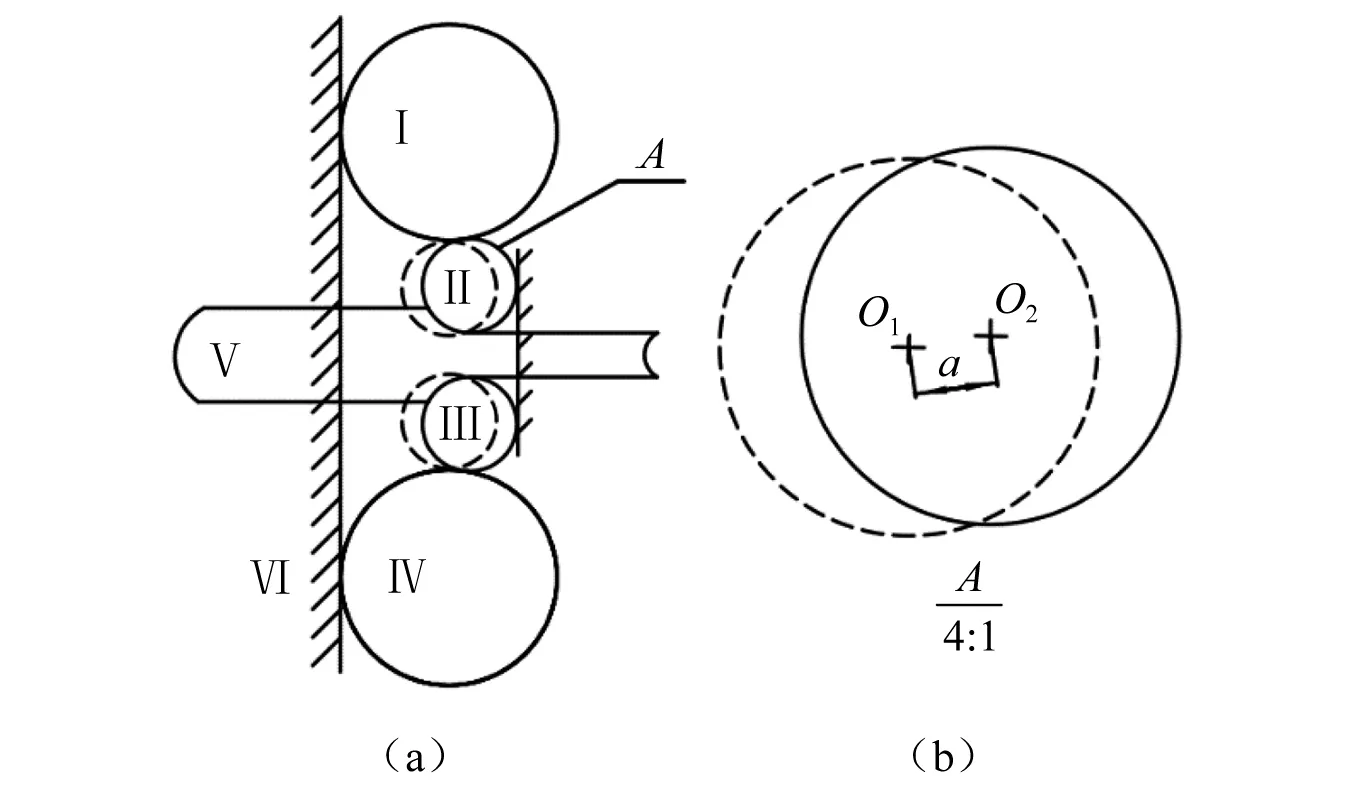
图1 四辊冷轧机结构

冷轧薄板能耗低，板形精度高，是未来轧制的工艺发展趋势。要想获得板形、表面、尺寸公差及性能满足要求的高质量冷轧薄板，就不能回避冷轧装备振动引发的轧件精度难以提高的问题。冷轧薄板的工艺实施中，轧件的轧薄程度远大于一般轧件，轧机于垂直方向的振动在轧件表面印记明暗相间条纹的发生概率，远比一般冷轧工艺严重。

一般而言，同步轧制的垂振主要表现为频率为100～200 Hz的三倍频垂振和频率为500～700 Hz的五倍频垂振。轧机垂振系统的三倍频振动频率通常是二阶频率，该振动会造成轧材厚度不均匀、断带，甚至破坏设备；五倍频的频率通常是轧机垂振系统的四阶频率，该振动会造成轧材表面明暗相间条纹，影响产品精度。目前的文献检索表明：垂振会在轧材成型精度、轧薄能力及轧制效率等方面产生不良影响[28]。

四辊冷轧机结构中的支承辊和工作辊，会因存在有不同程度的安装偏心，被轧制过程的力效应(会使机架窗口结构间隙偏移)、辊系热膨胀效应等因素放大，进一步加大辊系间的偏心；加之冷轧中轧件塑变、辊系弯曲和不对中等产生的偏心力，都会使垂向轧制力频繁波动和系统垂向辊缝的不均匀变化，进而影响轧材厚度成型一致性。另一方面，瞬态成型中的轧件不均匀厚度在垂向上反馈给轧制力形成误差复映的轧制力波动，二者形成了垂振系统内部的反馈和能量持续供给的颤振发生条件，导致垂直颤振的持续发生，进而造成轧材成型质量进一步下降。

1.2 冷轧垂直颤振建模

如图1所示的支承辊和工作辊偏心，考虑实际轧制过程的支承辊和工作辊的偏心量为a，两辊的等效质量为m，转速为ωB时，则偏心造成的离心力可写为

(1)

假设偏心初始相位角为φ0，则偏心作用在系统垂向上引起的偏心力为

(2)

在图1的结构中，考虑到轧机结构的对称性与振动的对称性，针对冷轧上部辊系结构，建立垂直颤振模型如图2所示。其中，工作辊和支承辊等效质量为m，与机架间一次方等效阻尼为c1，与机架间三次方等效阻尼为c3，与机架间一次方等效刚度为k，辊系的结构间隙为2b，轧制力记为F，以冷轧垂直方向静平衡位置为原点，向上为正方向，垂向振动位移为x。

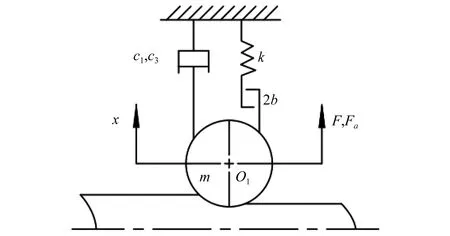
图2 冷轧垂直颤振模型

当偏心力的初始相位角为φ0=0时，偏心力为

(3)

机械结构间隙会减弱垂向系统刚度，降低抗变形能力，造成冷轧垂向的运动失稳。把含有垂向结构间隙的位移分段表达，如图3所示。弹性回复位移f(x)写作

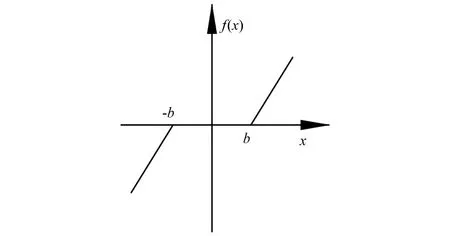
图3 冷轧系统垂向的结构间隙的弹性回复位移

(4)

在稳态轧制过程中，取冷轧垂直方向静平衡位置为原点，向上为正方向，则初始位置为-x0，由牛顿定律，可写出图2所示的冷轧垂直颤振的运动微分方程

(5)

平衡位置的轧制力和偏离初始位置的弹性回复力相抵消，存在轧制力F=kx0，冷轧垂直振动系统在平衡位置附近发生振动，可对式(5)化简得到

(6)

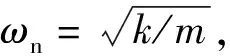
(7)

将式(7)代入式(6)，冷轧垂直颤振方程可化为

(8)

其中，

(9)

1.3 冷轧垂直颤振动力系统的势阱分析

令U(z)为式(8)的势能函数，可表示为

(10)

则冷轧垂直颤振动力系统的势阱，如图4所示。图4中：L0为势垒宽度；L1为势垒高度；P和W分别为对称的双势阱。冷轧系统发生垂直颤振，可以理解为系统中的机械构件表面的振动质点以振子群或孤立的质点(振子)的振动运动。振子群的运动范围在势阱P与W的势阱内部或它们的势阱外部的势垒壁之间。一方面，对称的势阱P和W间存在宽度为L0的势垒，该势垒平台能为轧制工艺提供稳定运行的参数选择空间，该参数域内实施的运行参数，保障轧制工艺系统的运动稳定性；另一方面，当振子进一步获得能量在势阱P和W间运动时，宽度为L0的势垒能为运动中的振子进一步提供趋向更不稳定的高能轨运动跳板，会使能量高的活跃振子在势阱两侧势垒壁外部，沿势阱壁间发生碰撞和冲击，造成冷轧工艺系统的垂直运动状态复杂化。

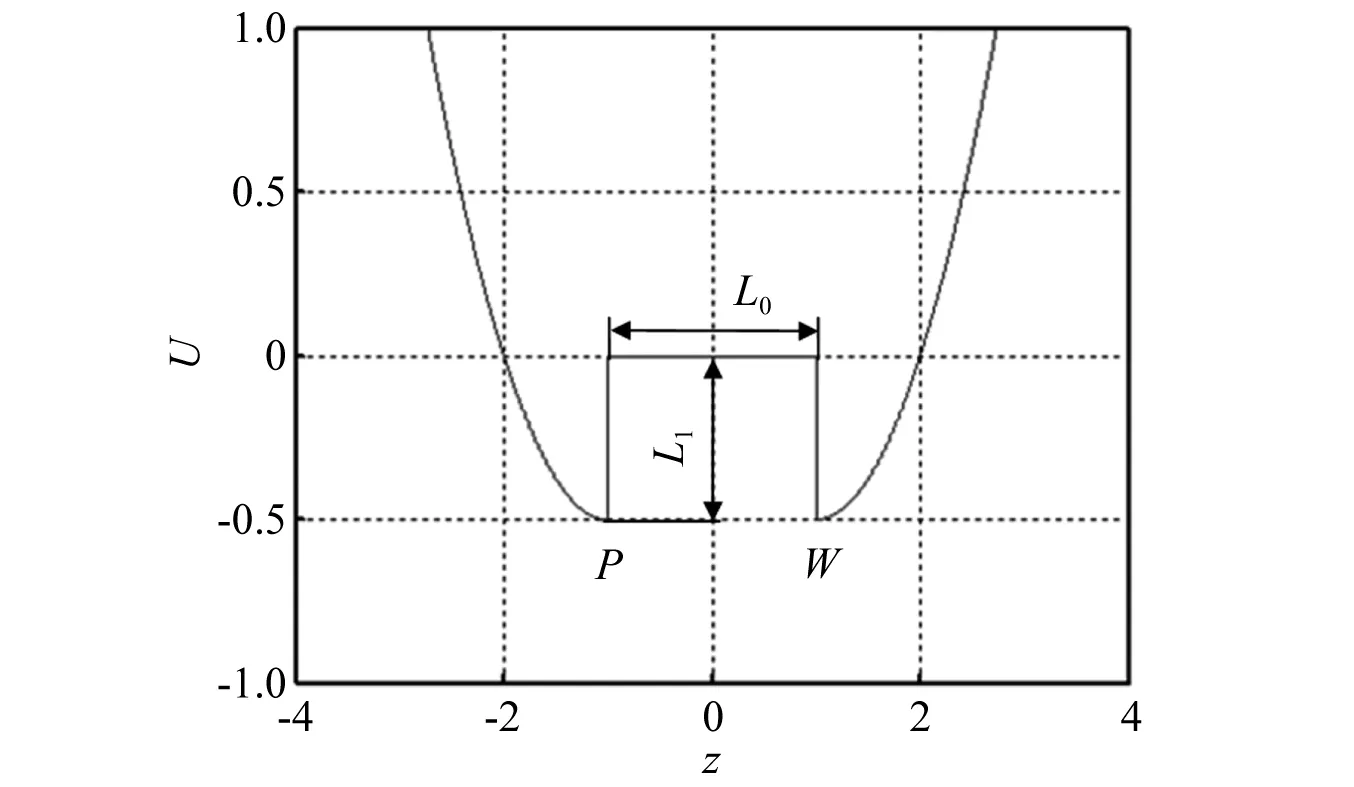
图4 冷轧垂直颤振势阱曲线

2 冷轧垂直颤振的单参分岔特性

动力系统中的参量变化，会改变系统方程解的结构，尤其当某参量在临界值附近发生微小变化时，会引起系统相空间轨线的拓扑突变，即形成分岔。考虑冷轧垂直颤振系统在三次方阻尼和间隙变化条件下的动特性，利用单参量变化的分岔和最大Lyapunov指数，探究系统的动力行为转化机制。利用式(8)对冷轧垂直颤振系统的单参量分岔特性分析，以明确单参量变化对系统运动失稳以及运动状态改变的作用。

采用变步长4～5阶Runge kutta法求解式(8)，以某厂2030轧机参数为例，上、下支承辊直径1 530 mm，上、下工作辊直径620 mm。其中：m=105×103kg；k=1.66×109N/m；c1=6.2×106N·s/m；c3=2.16×1010N·s/m；2b=0.176×10-3m。

2.1 频率比对冷轧垂直颤振的影响

冷轧垂直颤振的频率比Ω的分岔特性，如图5所示。频率比Ω变化时的最大Lyapunov指数，如图6所示。最大Lyapunov指数大于零，表明冷轧垂直颤振系统处于混沌运动状态，最大Lyapunov指数小于零，表明冷轧垂直颤振系统处于稳定的周期运动状态。

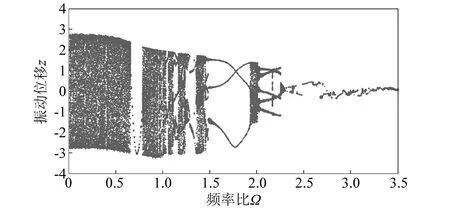
图5 频率比Ω变化下的分岔图

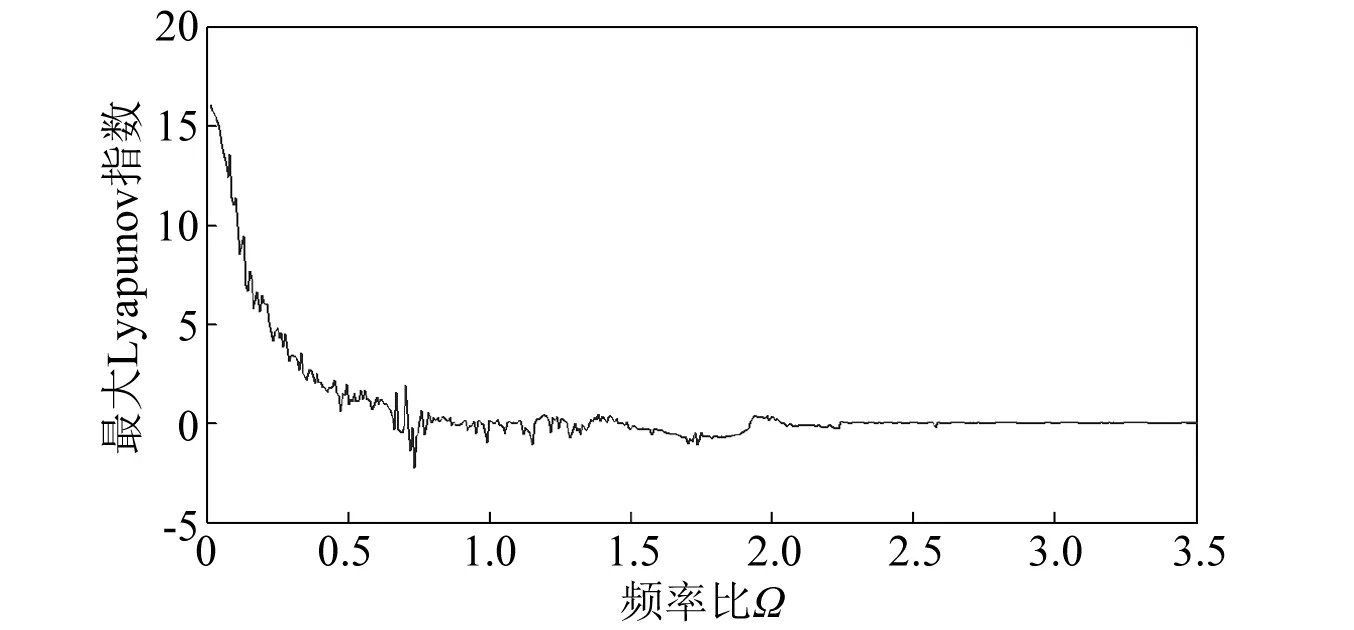
图6 频率比Ω变化下的最大Lyapunov指数图

综合图5和图6分析频率比Ω变化下的系统单参量分岔：当Ω<0.665时，最大Lyapunov指数大于零，系统处于混沌运动状态；当Ω∈(0.665，0.775)时，最大Lyapunov指数小于零但接近于零，系统做不稳定的单周期运动；随Ω单调递增至Ω∈(0.775，1.475)时，最大Lyapunov指数大于零且在零值附近小范围波动，系统总体呈现混沌状态，但存在瞬态的周期运动窗口；当Ω∈(1.475，1.935)时，最大Lyapunov指数小于零，系统做三周期运动；当Ω∈(1.935，2.035)时，最大Lyapunov指数大于零，系统做混沌运动；当Ω>2.035时，最大Lyapunov指数小于零，系统做周期运动。

可见，频率比Ω对冷轧垂直颤振工艺系统的影响，主要是通过Ω变化引起辊系的偏心力波动，进一步诱导和促发偏心力对冷轧轧制力的波动，造成轧材厚度不一致，影响轧件成型后的精度。因此，需要将频率比Ω控制在合理的工艺范围内。

2.2 一次方刚度对冷轧垂直颤振的影响

冷轧垂直颤振的一次方刚度k的分岔特性，如图7所示。一次方刚度k变化下的最大Lyapunov指数，如图8所示。综合图7和图8分析一次方刚度k变化下的系统单参分岔：当k<1.55×109N/m时，最大Lyapunov指数大于零，系统处于混沌状态；当k∈(1.55×109，1.64×109)N/m时，系统做周期运动；随k逐渐单调递增，系统大范围处于混沌运动，存在少部分的瞬态周期运动窗口。

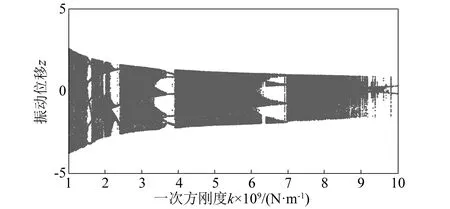
图7 一次方刚度k变化下的分岔图

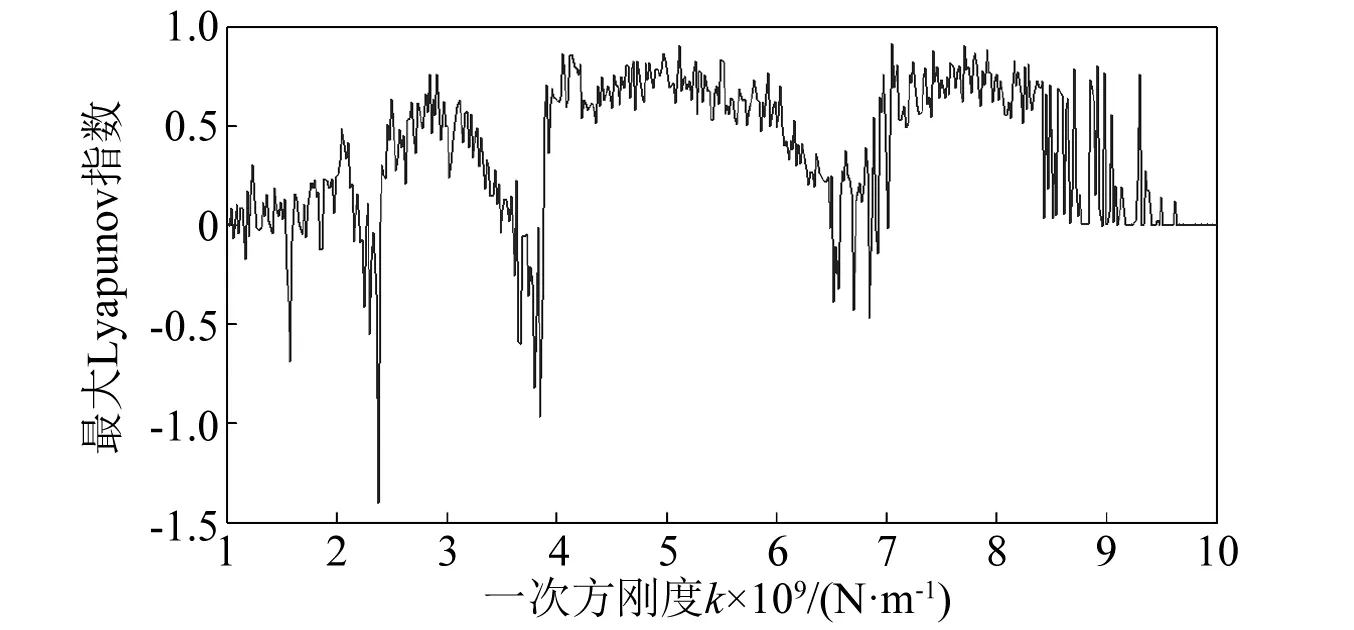
图8 一次方刚度k变化下的最大Lyapunov指数图

随一次方刚度k由小变大，冷轧垂直颤振系统历经混沌-周期-混沌-周期的运动状态交叠。从图7可知，k改变的多数区间，系统在大范围内做混沌运动，只出现小范围周期运动窗口，这也反映出k的改变对系统动特性的变化影响不明显。

2.3 一次方阻尼对冷轧垂直颤振的影响

冷轧垂直颤振的一次方阻尼c1的分岔特性，如图9所示。一次方阻尼c1变化时的最大Lyapunov指数，如图10所示。随一次方阻尼c1的单调递增，冷轧颤振系统历经周期-混沌-多周期-混沌-多周期-混沌-多周期-混沌的系列变化交叠。c1的变化会影响振动速度，进而导致冷轧垂直颤振动力系统的拓扑结构变化。从图9和图10可知，c1改变的多数区间，系统在大范围内做混沌运动，也存在小范围的周期运动窗口，这也反映出c1的改变对系统动特性的变化影响不明显。

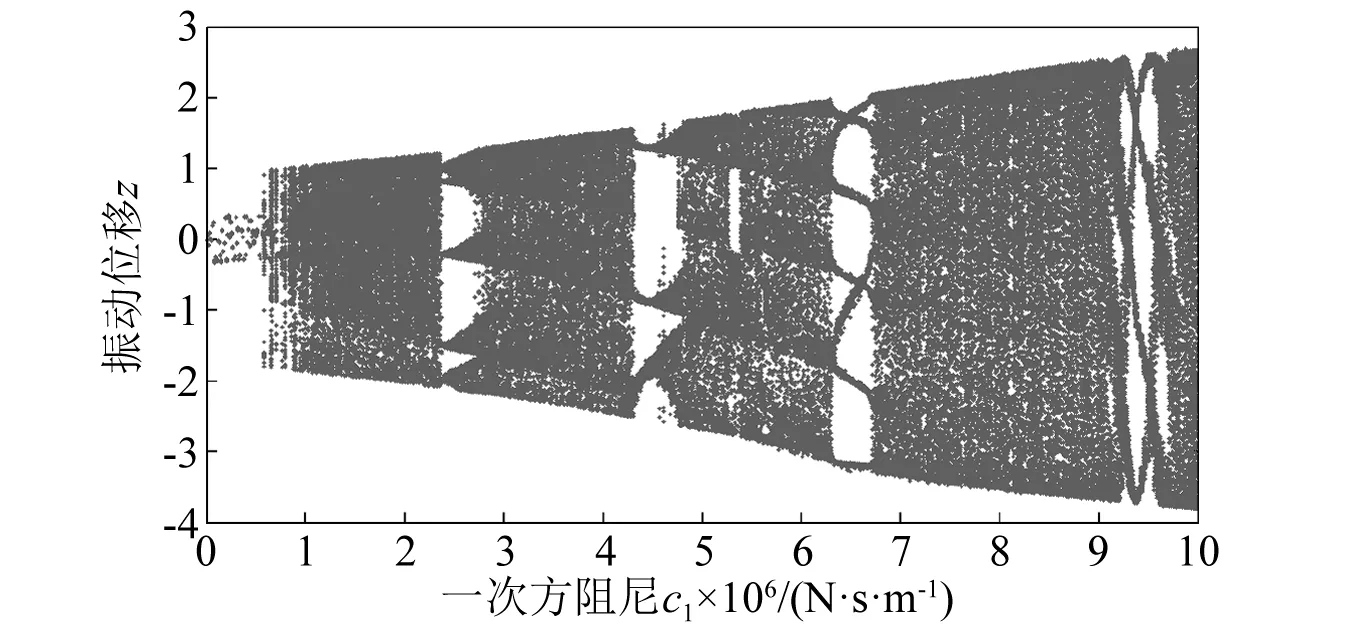
图9 一次方阻尼c1变化下的分岔图

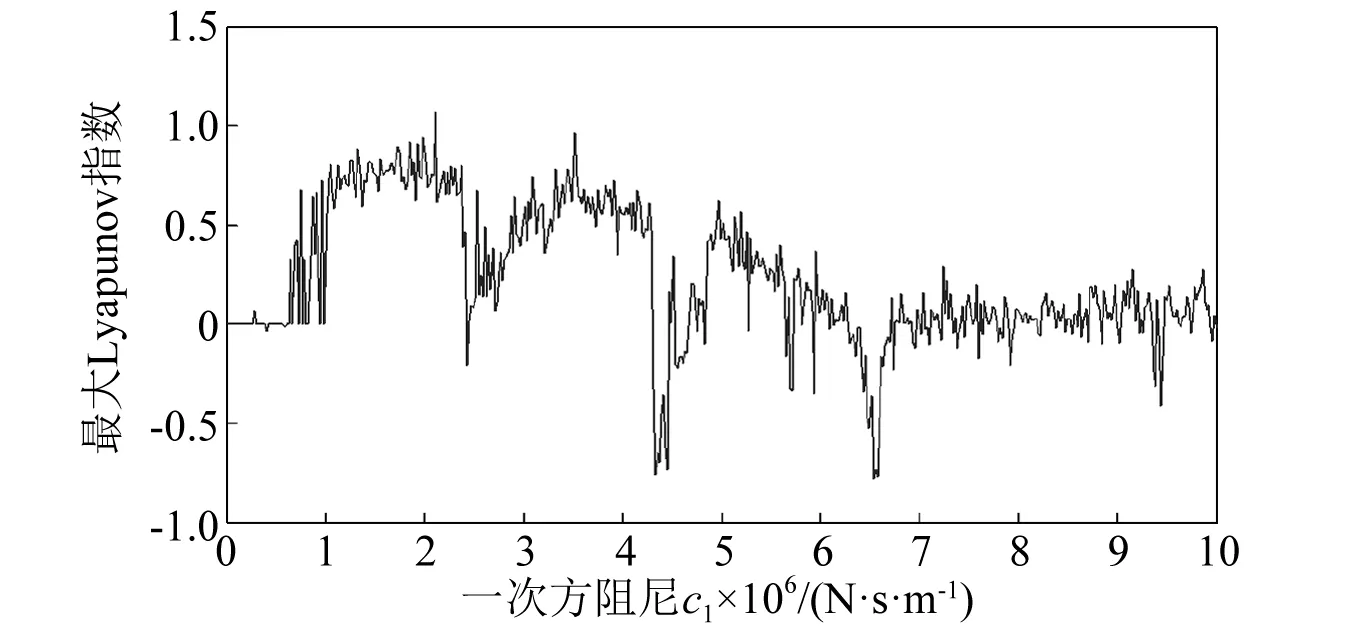
图10 一次方阻尼c1变化下的最大Lyapunov指数图

2.4 三次方阻尼对冷轧垂直颤振的影响

冷轧垂直颤振的三次方阻尼c3的分岔特性，如图11所示。三次方阻尼c3变化时的最大Lyapunov指数，如图12所示。随三次方阻尼c3单调递增，系统历经混沌-六周期-混沌-三周期-混沌-五周期-混沌的运动状态的交叠改变。三次方阻尼c3的变化，诱导和促发了冷轧颤振系统发生复杂的运动状态改变：当冷轧垂直颤振系统处于混沌运动时，运动状态将发生失稳，影响轧件产品质量。

图11 三次方阻尼c3变化下的分岔图

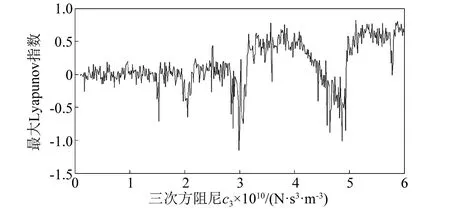
图12 三次方阻尼c3变化下的最大Lyapunov指数图

2.5 偏心量对冷轧垂直颤振的影响

冷轧垂直颤振的偏心量a的分岔特性，如图13所示。偏心量a变化时的最大Lyapunov指数图，如图14所示。随着偏心量a的单调递增，冷轧垂直颤振系统历经混沌运动-七周期运动-混沌运动-单周期运动。当偏心量a=1.045×10-4m时，最大Lyapunov指数由正变为负，系统由混沌运动进入单周期运动状态。

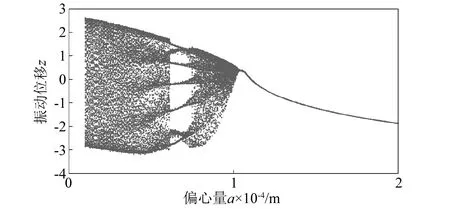
图13 偏心量a变化下的分岔图

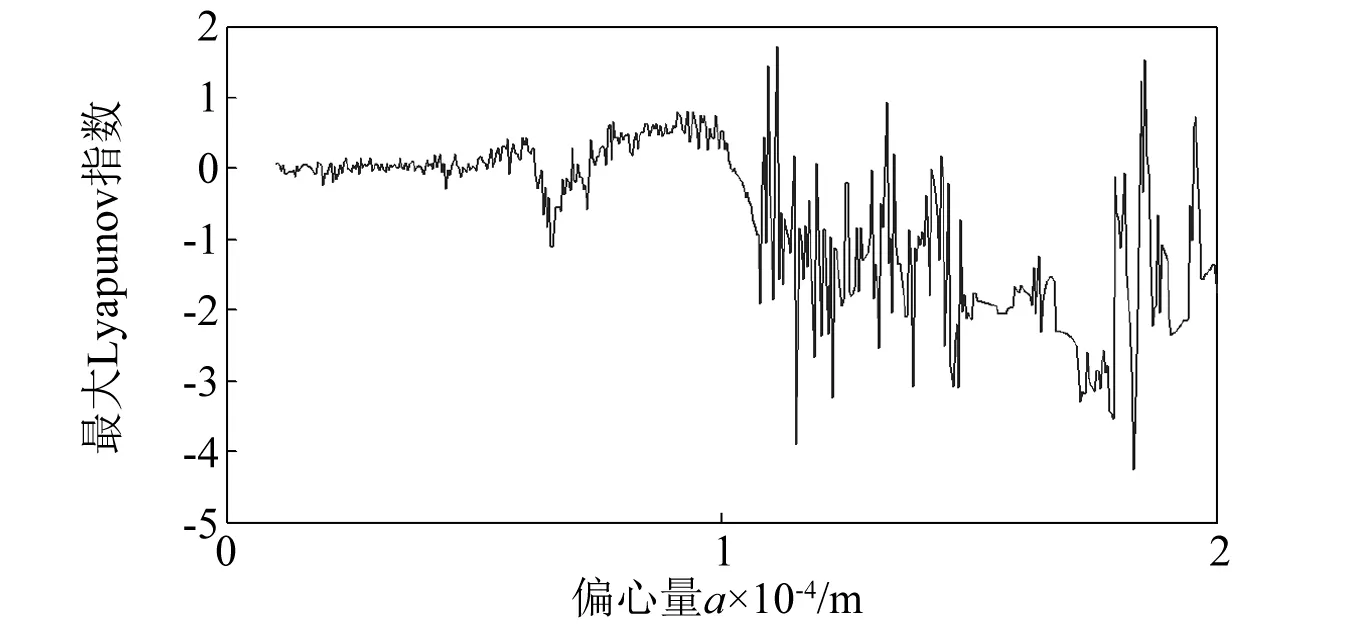
图14 偏心量a变化下的最大Lyapunov指数图

偏心量a的变化会改变偏心力的大小，也影响垂直方向上辊缝大小的变化。当偏心量a>1.045×10-4m时，冷轧垂直颤振系统做单周期运动，说明偏心量在一定程度上会增强冷轧结构垂直方向上的表现刚度；但当偏心量a较大时，将会使辊缝在较大范围内变化，将会降低轧制精度。在实际系统中，要合理进行偏心控制，进而有效保证轧件产品质量。

2.6 间隙对冷轧垂直颤振的影响

冷轧垂直颤振的间隙b的分岔特性，如图15所示。间隙b变化时的最大Lyapunov指数图，如图16所示。随间隙b的单调递增，冷轧垂直颤振系统历经混沌运动和周期运动的交替变化。冷轧机辊系与机架及其边界之间或大或小存在一定的间隙，在冷轧过程中，由于零部件磨损、变形等原因，都会导致间隙发生变化，诱导冷轧垂直颤振系统稳定性发生变化，发生复杂运动形式，进一步导致轧件产品质量降低。

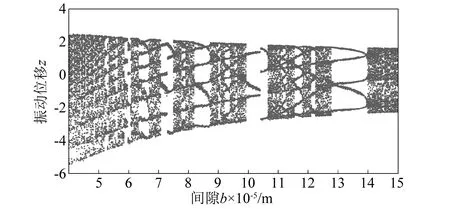
图15 间隙b变化下的分岔图

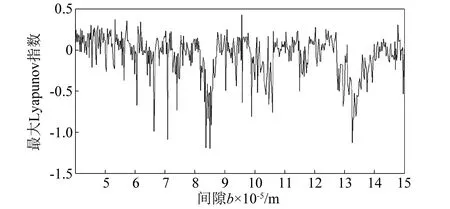
图16 间隙b变化下的最大Lyapunov指数图

3 冷轧垂直颤振的双参分岔特性

实际轧制过程的实施，是多参数共同作用的结果；反映了冷轧工艺系统作为复杂机电液系统的多输入多输出(multiple-input multiple-output，MIMO)关系，该系统的振动特性也受多工况参数的共同作用影响，对MIMO系统典型振动特性的分析会更复杂，利用系统方程最大Lyapunov指数能够表征系统混沌以及周期运动的特点[29]，对双参量变化下冷轧垂直颤振特性进行分析，冷轧垂直颤振系统在不同双参量组合平面上的分岔特性，如图17所示。图17中Ch1为最大Lyapunov指数大于零区域，表征系统做混沌运动。

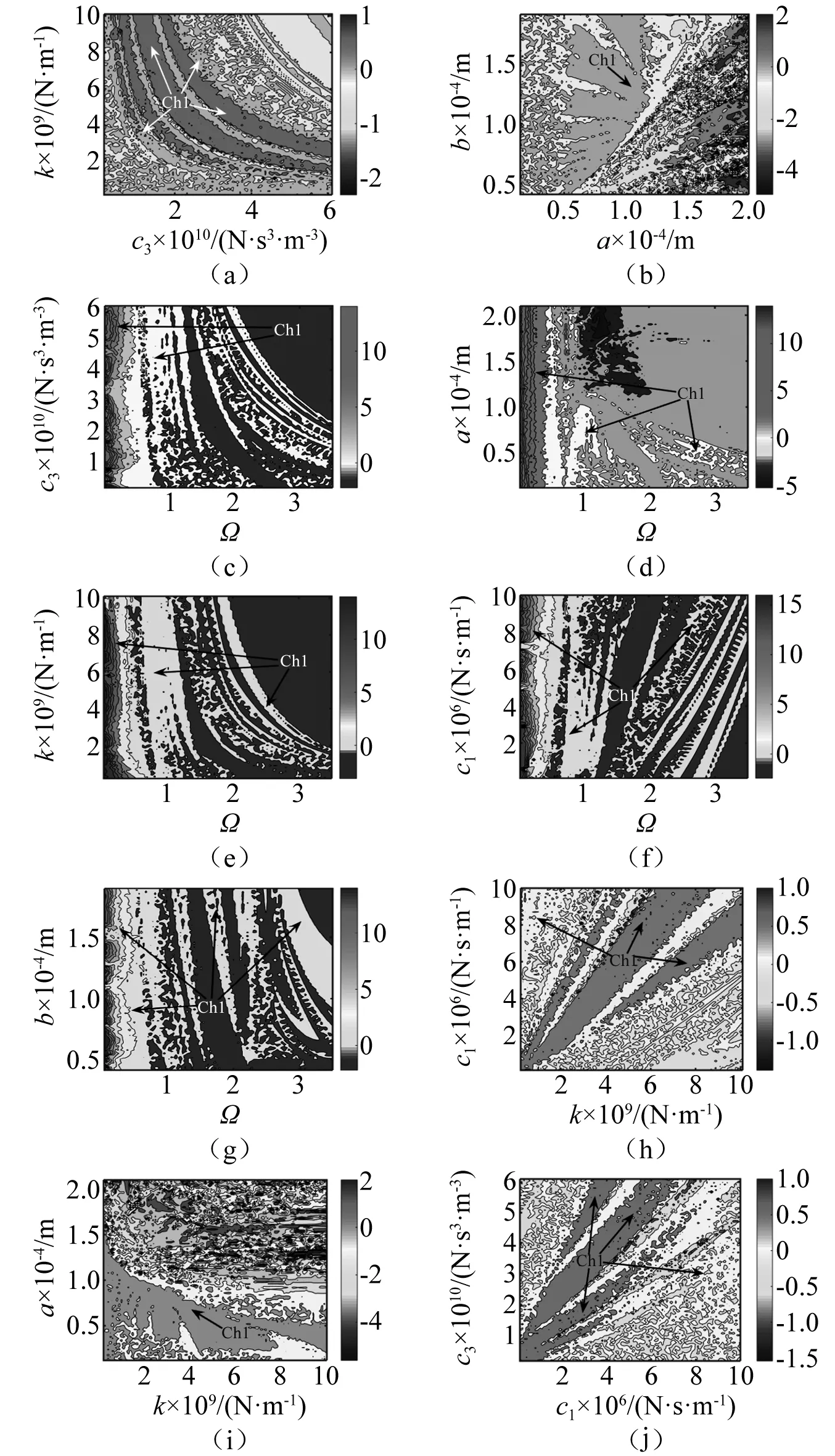
图17 双参量分岔特性图

图17(a)为三次方阻尼c3和一次方刚度k同时变化对冷轧垂直颤振特性的影响。Ch1区域表明系统做混沌运动，系统的运动不确定性增大，不利于保证轧件精度。图17(b)为偏心量a和间隙b同时变化对冷轧垂直颤振特性的影响。Ch1区域既有片状分布，也存在小区域分布，系统做混沌运动，该区域偏心量a和间隙b应该谨慎匹配选择，尽量避开混沌运动状态。

图17(c)为频率比Ω和三次方阻尼c3同时变化对冷轧垂直颤振特性的影响。当选择的频率比Ω和三次方阻尼c3匹配在Ch1区域时，系统将发生混沌运动，影响轧制产品质量，同时也会降低冷轧机组的稳定运行精度。图17(d)为频率比Ω和偏心量a同时变化对冷轧垂直颤振特性的影响。Ch1区域主要集中在左方和左下方，当选择的频率比Ω和偏心量a匹配在Ch1区域，系统做混沌运动。

图17(e)为频率比Ω和一次方刚度k同时变化对冷轧垂直颤振特性的影响。当选择的频率比Ω和一次方刚度k匹配在Ch1区域时，系统做混沌运动。当频率比Ω和一次方刚度k在Ch1区域边界处变化时，最大Lyapunov指数将会发生零附近的跃动，引发系统运动状态在混沌运动和周期运动的边界频繁转换。图17(f)为频率比Ω和一次方阻尼c1同时变化对冷轧垂直颤振特性的影响。Ch1区域所占比例较大，当选择的频率比Ω和一次方阻尼c1匹配在Ch1区域时，系统做混沌运动。

图17(g)为频率比Ω和间隙b同时变化对冷轧垂直颤振特性的影响，当选择的频率比Ω和间隙b匹配位于Ch1区域时，系统做混沌运动，不利于保证轧件产品精度。图17(h)为一次方刚度k和一次方阻尼c1同时变化对冷轧垂直颤振特性的影响。当选择的一次方刚度k和一次方阻尼c1匹配在Ch1区域时，系统最大Lyapunov指数大于零，系统做混沌运动。

图17(i)为一次方刚度k和偏心量a同时变化对冷轧垂直颤振特性的影响。Ch1区域主要分布在下方，并且在上部呈现“雨滴状”散布，当选择的一次方刚度k和偏心量a匹配在Ch1区域时，系统做混沌运动。图17(j)为一次方阻尼c1和三次方阻尼c3同时变化对冷轧垂直颤振特性的影响。Ch1区域占据了图中主要部分，当选择的一次方阻尼c1和三次方阻尼c3匹配在Ch1区域时，系统做混沌运动，不利于保证轧件产品质量。

通过探究冷轧工艺过程中的相关双参量的匹配变化对冷轧垂振系统颤振特性的发展变化的影响规律，能为冷轧系统的规划设计以及轧制工艺参数的运行制定提供参考，合理选取与匹配相关的冷轧参数，规避不利于轧制稳定工作的工艺参数，有利于提高轧件产品质量、精度及保证轧制装备生产线的稳定运行。

4 结 论

本文以冷轧工艺过程的垂直颤振为研究对象，建立了考虑三次方阻尼和间隙变化下的冷轧垂直颤振模型，依次对系统进行了势阱分析、结合最大Lyapunov指数图的单参分岔特性分析、双参分岔特性分析，结论如下：

(1)冷轧垂直颤振系统的势阱，存在一定宽度的势垒，该势垒若运用得当，可通过选择匹配适合的运行参数，输出的系统动特性如势垒平台一样，是个稳定的运行平台，可保证轧制工艺系统的稳定运行；同时，该势垒也为运动中不断吸能的高能振子(质点)提供了能轨跃迁的跳板，活跃振子能轨的迁移运动，会使振子群发生冲击和碰撞到两侧的势垒壁上，促发冷轧垂振系统工艺状态的运动趋向复杂化。

(2)通过探究系统的单参分岔特性，得到系统随频率比Ω、一次方刚度k、一次方阻尼c1、三次方阻尼c3、偏心量a和间隙b等单参量变化的运动发展趋势，表明冷轧垂直颤振系统的运动状态随上述单参量的改变，不断在周期运动、混沌运动以及各类复杂运动状态之间转换变迁。

(3)通过分析系统的双参分岔特性，得到了双参量匹配变化时，系统做周期运动和混沌运动的参数区域，表明双参量约束变化下，冷轧垂直颤振系统的动力学特性表现更加丰富。

通过上述研究和分析过程，明确了冷轧工艺过程发生垂直颤振时，系统混沌运动和周期运动的不同双参量匹配区域。本文的研究揭示了冷轧垂直颤振系统发生混沌运动以及周期运动的参数变化规律，为冷轧工艺参数规划设计及抑振减振提供了理论参考。