短码长四元最优局部修复码的构造

李瑞虎 展秀珍 付 强 张 茂 郑尤良

(空军工程大学基础部 西安 710051)

1 引言

在分布式存储系统中，三重备份能够保证数据的可靠性，并且它是最简单的方法[1]。然而三重备份的存储效率低、存储代价过大，于是人们提出了存储负荷更低的纠删码方案[2,3]。传统纠删码能满足高效存储的需求，但是修复效率低，因此编码学者提出了局部修复码[3]。2012年，Gopalan等人[4]提出LRC的概念以及Singleton-Like (S-L)界，但是SL界在小域[4,5]上是不紧的。为了更加精确地描述q元局部修复码4个参数之间的关系，Cadambe和Mazumdar[6]提出考虑域的大小的界，即Cadambe-Mazumdar (C-M)界。

在工程应用中，小域上LRC的编、解码复杂度较低，更具有使用价值[7]。二元域上LRC取得一定进展，人们研究了达到S-L界[8,9]以及C-M界[10,11]的局部度最优LRC。文献[12,13]研究了三元距离较小或者维数较低的局部度最优LRC。在四元域上，人们得到一些局部度最优LRC：文献[14]构造了2类距离为3的四元LRC；文献[15]构造了距离为4的四元LRC；这3类LRC是局部度最优和拟最优的[14,15]。Barg等人[16]利用代数曲线和代数曲面构造了码长为18、维数为11、距离为3、局部度为2的四元LRC。文献[17]通过缩短q元汉明码与(q2+1)−cap构造了距离为3和4的LRC，从而可得到16个距离为3和12个距离为4的局部度最优四元LRC。Jin等人[18]利用有限域上的自同构群构造一般域上LRC，可得到码长不超过5的四元LRC。由以上结果可知，当码长不超过20时，文献[14,15,16]构造了特定距离的局部度最优或拟最优四元LRC，但只有1个码是距离最优码；文献[17]的2个四元LRC以及文献[18]的1个四元LRC都不是距离最优码。

由文献[19]可知，当域的大小为2的幂次时，码的运行速度快，并且文献[20]给出了RS码校验关系的等价转换方式，避免了复杂的符号转化。依据文献[21-23]，码长不超过20的距离最优四元码的参数完全确定。由文献[23]可知，对于给定的码长和维数，距离最优四元码往往有很多，但是它们的局部度也有差别，人们往往更关注局部度尽可能小的LRC。基于此本文研究四元LRC，由已有文献结果可知，目前四元LRC的研究并不充分，其结果较为零散，因此本文将研究码长不超过20的四元码，设法构造距离最优且局部度尽可能小的四元LRC，并利用S-L界或C-M界判断其局部度的最优性。

2 预备知识

令F4={0,1,ω,ω2}为四元域， 记ω=2，ω2=3，F4={0,1,2,3}。F4n为F4上的n维向量空间，若一个非零向量的第1个非零分量是1，则称此向量为首一向量。称F4n的k维子空间C为四元线性码[n,k]4，并记为C=[n,k]4，n称为C的码长，C中的向量称为码字。

引理1[4]设线性码C=[n,k,d]q的生成阵为Gk,n=(g1,g2,...,gn)，gi是k维列向量，当i ∈[n]时，若存在大小不超过r的子集Ai ⊆[n]{i}使得gi被至多r个gj(j ∈Ai)线性表出，则C的局部度为r。

引理2[9]H=(HlT,Hn−k−lT)T为线性码[n,k,d]q的校验阵，Hl中的列均为非零列向量，Hl的行称为H的局部度行。若Hl的行向量的汉明重量不超过r+1，则C的局部度为r。

下面介绍常用的S-L界和C-M界。

引理3[4,6]若C=[n,k,d;r]q存在，式(1)和式(2)成立时，分别称为S-L界[4]与C-M界[6]

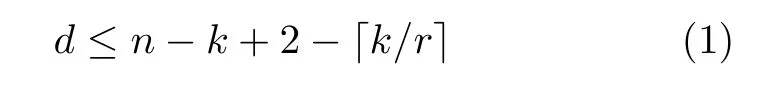
等式成立时，称码达到S-L界。特别地，当k=r时，S-L界退化为经典的Singleton界。

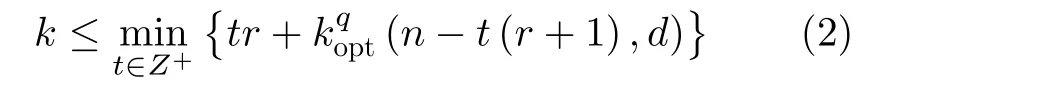
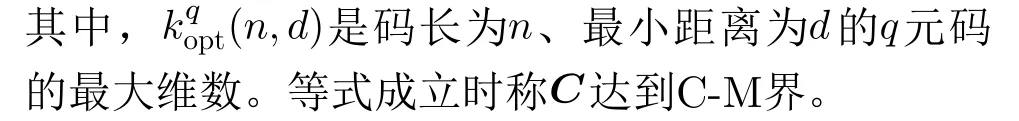
若C=[n,k,d;r]q达到S-L界或C-M界，或者[n,k,d;r −1]q的局部修复码不存在，则称C是局部度最优的(r−最优的)。

约定：[n,k,d]4简记为[n,k,d]；[n,k,d;r]4简记为[n,k,d;r]。in=(i,i,...,i)(i=0,1,2,3)表示长度为n且分量为i的行向量，iTn=(i,i,...,i)T为in=(i,i,...,i)的转置。[n]={1,2,...,n}，并约定n ≤20；In为n阶单位阵。记Gk,m的l个并置为Gk,lm=(Gk,m,Gk,m,...,Gk,m)=(lGk,m)。

3 F4上短码长LRC的构造

码长n ≤20的距离最优码共2 1 0 个，其中[n,n,1]码不具有局部修复功能，还余下190个距离最优码。对于n ≥2，1n生成[n,1,n;1]码，其对偶码为[n,n −1,2;n −1]，此两码达到S-L界。故以下仅需考虑[n,k,d]和[n,n −k,d′](k ≥2)形式的局部修复码构造，分7个小节展开讨论。

由文献[22,23]，分以下3步构造距离最优码的生成阵Gk,n：

步骤1 由文献[22,23]得到距离最优码的生成阵，利用四元域中的乘法运算将生成阵中的列向量化为首一列向量；

步骤2 将首一列向量按照列汉明重量由小到大的顺序排列；

步骤3 对排序后的生成阵做列置换，依次删除生成阵Gk,n的最后j(1≤j

3.1 参数为[n,2,d]和([n,n−2,d′]的)LRC

以上构造的LRC都是距离最优码，其中r=1的LRC的局部度已达到最小；码长3≤n ≤10(n ̸=7,9)的[n,2,d;r]码和n ≥6的[n,n −2,2;「(n −2)/2■]达到S-L界；[7,2,5;2]和[9,2,7;2]达不到S-L界和C-M界，但不难验证[7,2,5;1]和[9,2,7;1]不存在，故这两个码仍是r−最优的。

3.2 参数为[n,3,d]和[n,n −3,d′]的LRC

3.3 参数为[n,4,d]和[n,n −4,d′]的LRC

记G4,n=(I4|B4,n−4)，构造如式(5)的5个矩阵，G4,17由文献[17]给出

G4,6和G4,10分别生成[6,4,2;2]和[10,4,6;3]码。删除G4,10的后i(1≤i ≤3)列，可得[9,4,5;3]，[8,4,4;3]和[7,4,3;3]码。G4,23生成[23,4,16;2]码，删除G4,23的后i(1≤i ≤4)列可得[22,4,15;2]，[21,4,14;2]，[20,4,13;2]和[19,4,12;2]码。G4,17添加G4,17中的1列可得[18,4,12;3]，由文献[17]删除校验阵G4,17的列可得到[n,n −4,4;rn]，9≤n=17−j ≤17，其中n=9,10,...,16,17时局部度分别为rn=4,5,6,6,7,8,9,10,11。记G4,17=(β1,β2,...,β17)，令G4,n=(β1,β2,...,βn) ，(11≤n=17−j ≤17)，G4,n生成[n,4,12−j;3]码。以H4,21为校验阵的码为[21,17,3;9]。当1≤i ≤3时，删除H4,21的后i列得到[20,16,3;9]，[19,15,3;8]和[18,14,3;7]码。以上构造的LRC都是距离最优码，其中6≤n ≤10的[n,4,d;r]码和9≤n ≤17的[n,n −4,4;r]码达到S-L界; 达到C-M界的L R C 为11≤n ≤23(n ̸=19)的[n,4,d;r]以及18≤n ≤21的[n,n −4,3;r]；而[19,4,12;2]LRC达不到S-L界和C-M界。

3.4 参数为[n,5,d]和[n,n −5,d′]的LRC

记G5,n=(I5|B5,n−5)，构造以下7 个矩阵，Xi=(γ1,γ2,...,γi)(4≤i ≤6)：

由G5,n分 别 可 得[7,5,2;3]，[11,5,6;4]，[14,5,8;3]，[17,5,10;3]和[24,5,16;2]码。由G5,11的子矩阵可得[10,5,5;4]，[9,5,4;4]，[8,5,3;4]码；由G5,14的子矩阵可得[13,5,7;3]，[12,5,6;4]码；由G5,17的子矩阵可得[16,5,9;3]，[15,5,8;3]码。当1≤i ≤6时，依次删除G5,24的后i列分别可得[23,5,15;3]，[22,5,14;3]，[21,5,13;2]，[20,5,12;3]，[19,5,11;3]，[18,5,10;2]码。以H5,3i(i=4,5,6)为校验阵的码为[12,7,4;3]，[15,10,4;4]和[18,13,4;5]。删除H5,3i(i=5,6)的最后1 列可分别为[14,9,4;4]与[17,12,4;5]；删除H5,15的第10和15列得到[13,8,4;4]码，删除H5,18的第12和18列可得[16,11,4;5]码。H5,18依次添加列向量(1,1,1,2,3)T和(1,2,3,1,1)T得到H5,19与H5,20, 以H5,19为校验阵的码为[19,14,4;6]，以H5,20为校验阵的码为[20,15,4;7]。以上构造的LRC都是距离最优码，其中7≤n ≤11的[n,5,d;r]和12≤n ≤20(n ̸=13)的[n,n −5,4;r]码达到S-L界；12≤n ≤24(n ̸=19,20)的[n,5,d;r]码以及[13,8,4;4]码达到C-M界；而[19,5,11;3]和[20,5,12;3]码达不到S-L界和C-M界。

3.5 参数为[n,6,d]和[n,n −6,d′]的LRC

记G6,n=(I6|B6,n−6)，构造以下7个矩阵，横线以上的行为校验阵的局部度行。

由G6,12和G6,12的子矩阵可得[12,6,6;5]和[11,6,5;5]码；由G6,15和G6,15的子矩阵可得[15,6,8;4]，[14,6,7;4]和[13,6,6;4]码；由G6,18和G6,18的子矩阵可得[18,6,10;4]，[17,6,9;4]，[16,6,8;4]码；由G6,20和G6,20的子矩阵可得[20,6,11;3]和[19,6,10;3]码。以H6,14为校验阵的码为[14,8,5;5]，删除H6,14的最后1列得到[13,7,5;4]码；以H6,17为校验阵的码为[17,11,5;7]，依次删除H6,17的后2列得到[16,10,5;6]和[15,9,5;5]码；由H6,21可得[21,15,5;11]，删除H6,21的后3列得到[20,14,5;10]，[19,13,5;9]，[18,12,5;8]码。以上构造的LRC均为距离最优码，其中[11,6,5;5]和[12,6,6;5]码达到S-L界；13≤n ≤18的[n,6,d;4]及13≤n ≤21的[n,n −6,5;r]码达到CM界；而[19,6,10;3]和[20,6,11;3]码达不到S-L界和C-M界。

3.6 参数为[n,7,d]和[n,n −7,d′]的LRC

记G7,n=(I7|B7,n−7)，构造4 个矩阵(见下页)。矩阵G7,n分别生成[16,7,8;5]，[18,7,9;5]和[20,7,10;5]码；删除这3 者的最后1 列分别得到G7,n−1(n=16,18,20)及其生成的[15,7,7;5]，[17,7,8;5]和[19,7,9;5]码。以H7,20为校验阵得到[20,13,6;7]码，依次删除H7,20的后i(1≤i ≤6)列得到[19,12,6;7]，[18,11,6;6]，[17,10,6;6]，[16,9,6;5]，[15,8,6;5]，[14,7,6;4]码。以上构造的LRC都是距离最优码，其中15≤n ≤18的[n,7,d;r]和14≤n ≤20的[n,n −7,6;r]码达到C-M界；而[19,7,9;5]和[20,7,10;5]码达不到S-L界和C-M界。

3.7 参数为[n,k ≥8,d]和[n,n −k,d′]的LRC

构造以下7个矩阵，如式(9)，以H8,17为生成阵的码为[17,8,8;6], 其前16列生成[16,8,7;6]码；以H8,17为校验阵的码为[17,9,7;7]。由校验阵H8,21可得[21,13,6;8]码，删除H8,21的后s(1≤s ≤3)列可得到[20,12,6;7], [19,11,6;7]和[18,10,6;6]码。由H9,18可得[18,9,8;7]码，删除H9,18的最后1 列可得[17,8,8;6]码。由校验阵H9,21可得[21,12,7;8]码，删除H9,21的后i(1≤i ≤2)列可得[21−i,12−i,7;8−i]码。以H10,20为校验阵的码为[20,10,8;7]码，删除H10,20的后i(1≤i ≤2)列可得[20−i,10−i,8;7−i]码。由校验阵H11,22可得[22,11,8;7]码，删除H11,22的后s(1≤s ≤3)列可得[21,10,8;6]，[20,9,8;5]和[19,8,8;5]码。以上构造的LRC均为距离最优码，其中[n,n −8,7;r](n=16,17), 19≤n ≤21的[n,n −9,7;r], [n,n −9,8;r] (n=17,18), 18≤n≤20的[n,n −10,8;r]以及20≤n ≤23的[n,n −12,9;r]达到C-M界；而[n,n −8,6;r](18≤n ≤20), [19,8,8;5]和[20,9,8;5]达不到S-L界和C-M界。

四元距离最优LRC的构造结果：码长n ≤20的距离最优码共210个，除[n,n,1]码外的190个距离最优码具有局部修复功能，其中d=2的码共34个且达到S-L界。表1给出剩下的156个LRC[n,k,d;r]，达到S-L界的67个LRC用蓝色表示；达到C-M界的75个LRC用黑色表示；红色表示12个达不到S-L界和C-M 界且非r−最优的L R C；[7,2,5;2]和[9,2,7;2]达不到S-L界和C-M界，但它们仍是r−最优的。经查阅已有文献，这些构造结果包含了文献[15]中参数为[7,4,3;3]的四元LRC，以及文献[17]中的16个d=3和12个d=4的四元LRC，具体参数为[17−s,13−s,4;11−s](0≤s ≤5)，[12−j,8−j,4;6−3i −t](j=4i+t,0≤t ≤3,0≤i ≤1)及[21−s,18−s,3;15−s](1≤s ≤9)和[12−j,9−j,3;6−2i−t](1≤j=3i+t ≤4,0≤t ≤2,0≤i ≤2)。此外，还包含文献[1 8]中参数为[2,1,2;1]，[4,1,4;1]，[4,3,2;3]，[3,2,2;2]，[5,4,2;4]的5个四元LRC。

表1 d ≥3 , n ≤20时四元LRC的结果

4 结束语

本文研究了四元域上局部度较小的短码长LRC的构造，通过分析四元距离最优码的码长和维数，首先利用其生成阵或校验阵构造少量参数优良的LRC，然后删除或并置已有矩阵得到新LRC的生成阵或校验阵，最后利用S-L界或C-M界判断LRC的局部度最优性。与文献[15,17,18]比较，本文构造的四元LRC都是距离最优码且其结果更具有一般性，这对研究四元域上其他LRC的构造有很好的借鉴意义。在未来的工作中，将进一步研究四元域上码长和维数均较大时最优LRC的新构造。