忆阻开关混沌电路及其吸引子共存现象研究
2022-01-04马铭磷李志军
马铭磷 刘 颖 李志军
(湘潭大学自动化与电子信息学院 湘潭 411105)
1 引言
1971年,美籍华裔科学家蔡少棠根据电路基本变量组合完备性原理预测了描述电荷与磁通关系元件的存在,并将其定义为忆阻器[1]。到2008年,惠普公司实验室研究人员首次物理实现了忆阻器并在《Nature》 杂志上进行了报道[2]。忆阻器由于其非线性和记忆特性,在图像加密[3,4]、神经网络[5-8]、语音通信[9,10]、逻辑运算[11]、非线性混沌电路系统[12-14]等领域中都具有重大的潜在应用价值。最近几年,对于忆阻器模拟器电路设计的成果也很丰富,典型的如谭志平等人[15]提出的浮地型忆阻器模拟电路;Wang等人[16]提出的多分段线性忆阻模拟电路;Bao等人[17]提出的1阶广义电压控制型忆阻器模型。由于忆阻器具有非线性和记忆特性,基于忆阻的混沌电路比传统的非线性电路具有更为复杂的动力学行为。
混沌系统不仅仅可以产生混沌吸引子,当系统参数在特定的情况下,根据初始条件的不同系统的运行轨迹也可能发生变化,从而产生几个独立的吸引子,形成多吸引子共存现象[18]。由于不同的状态变量初始值可以将系统引向不同的吸引子,每个吸引子所对应的所有初始条件的集合就构成其吸引域。当系统的初始条件位于各个吸引域的边界时,系统中只要有微小的噪声存在都可能导致系统的运行轨迹发生变化,往往具有很复杂的动力学行为,这就导致了系统的运行轨迹变得不可预测。在实际应用中如果出现这种多吸引子共存现象会对电路的运行造成很大的影响,值得深入了解和研究。
目前对于分岔理论的研究大多是针对光滑动力系统进行的,而对于开关电路的动力学行为研究较少。近年来人们发现在开关电路中存在着丰富的非线性现象,边界碰撞分岔是开关系统中很常见的问题,在机械振荡器[19]、分段线性电路[20,21]和电力电子设备[22,23]中都可以找到边界碰撞分岔的例子。这些研究表明边界碰撞分岔可以直接导致系统运行轨迹发生变化。边界碰撞中有一类特殊的分岔,其在分岔点同时产生多个共存吸引子[24]。当系统参数平稳变化时,在分岔点之后共存吸引子的吸引盆非常接近,以至于系统中存在的噪声可以把系统运行轨迹从一个吸引子转移到另一个吸引子。这就导致不可能预测系统在分岔之后运行轨迹将跟随哪个吸引子,这是系统中不确定性的根本原因,称这种分岔为多吸引子分岔。文献[25]首次提出了一个具有多吸引子分岔的开关电路,在该系统分岔点之后出现了周期3极限环与混沌吸引子共存的现象,并验证了多吸引子分岔在电路中的可实现性。
开关电路是典型的非线性系统,本文在文献[25]的基础上提出了一种包含两个参考电压和一个忆阻器的开关电路。由于忆阻器对流经的电荷具有记忆作用,因此基于忆阻器的电路能出现更丰富的非线性现象。本文提出的电路产生了非常复杂的非线性动力学行为,文中论述了随系统初始值的改变而出现的多吸引子共存行为,包括不同混沌吸引子的共存、不同周期极限环的共存,以及周期极限环与混沌吸引子共存等现象。电路中存在的多吸引子共存现象对系统的运行可能带来不可预计的破坏性,为了设计稳定可靠的开关电路,有必要对其运行机制进行深入了解,避免其产生一些非理想的破坏性结果。本文为进一步探索开关电路中混沌的应用以及对多吸引子共存现象的研究具有重要意义。
2 电路描述
本文所提忆阻开关混沌电路如图1所示,其中包含一个方波电压源V(t),两个电容C1和C2,一个电感L,两个电阻R和RC,两个电压比较器U1和U2、两个参考电压Vref和-Vref、两个开关S1和S2、一个忆阻器RM。其中比较器U1和比较器U2分别控制开关S1和S2的闭合以及断开。根据开关S1和开关S2的状态不同,图1所示开关电路的工作拓扑也随之改变。

图1 忆阻开关混沌电路图
图2所示为文献[17]所提出的电压控制型忆阻器RM的等效模型,其中包括1个运算放大器U,3个电阻Ra, Rb和Rd, 1个电容C0以及2个乘法器M1和M2,值得一提的是,并联电阻Rb可以避免直流电压积分漂移,因此选用图2所示忆阻器模型更适合硬件实验。图2所示的忆阻电路是一个一端接地的单端电路,其电路方程如式(1)所示
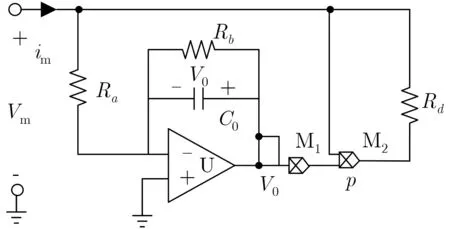
图2 忆阻器RM等效电路



则系统方程式(2)转换后的无量纲状态方程组为
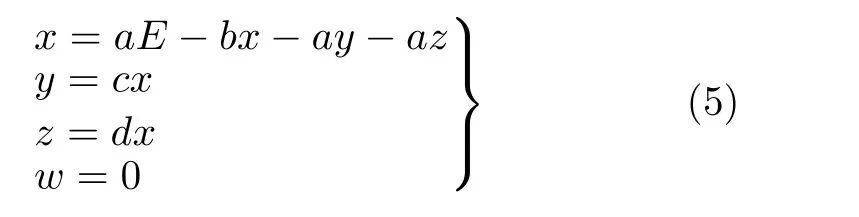
则系统方程式(3)转换后的无量纲状态方程组为

则系统方程式(4)转换后的无量纲状态方程组为
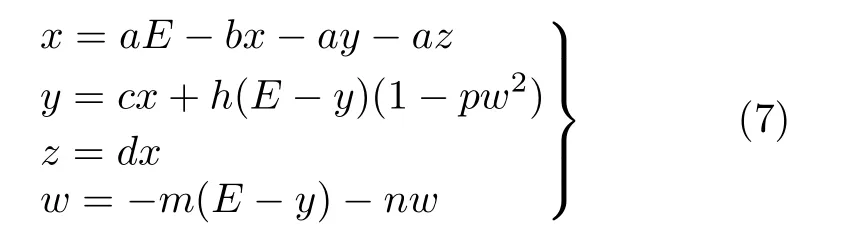
在此电路中,当开关S1和S2断开时,由于其输入电压为方波,当输入电压的幅值达到一定值时,此电路的工作状态在图3(a)、图3(b)、图3(c) 3种电路状态下不停变换;同样当开关S1或S2闭合时,由于其输入电压为方波,电路的工作状态也在图3(a)、图3(b)、图3(c)3种电路状态下不停变换,且在同一时间电路只工作在其中一种状态下。
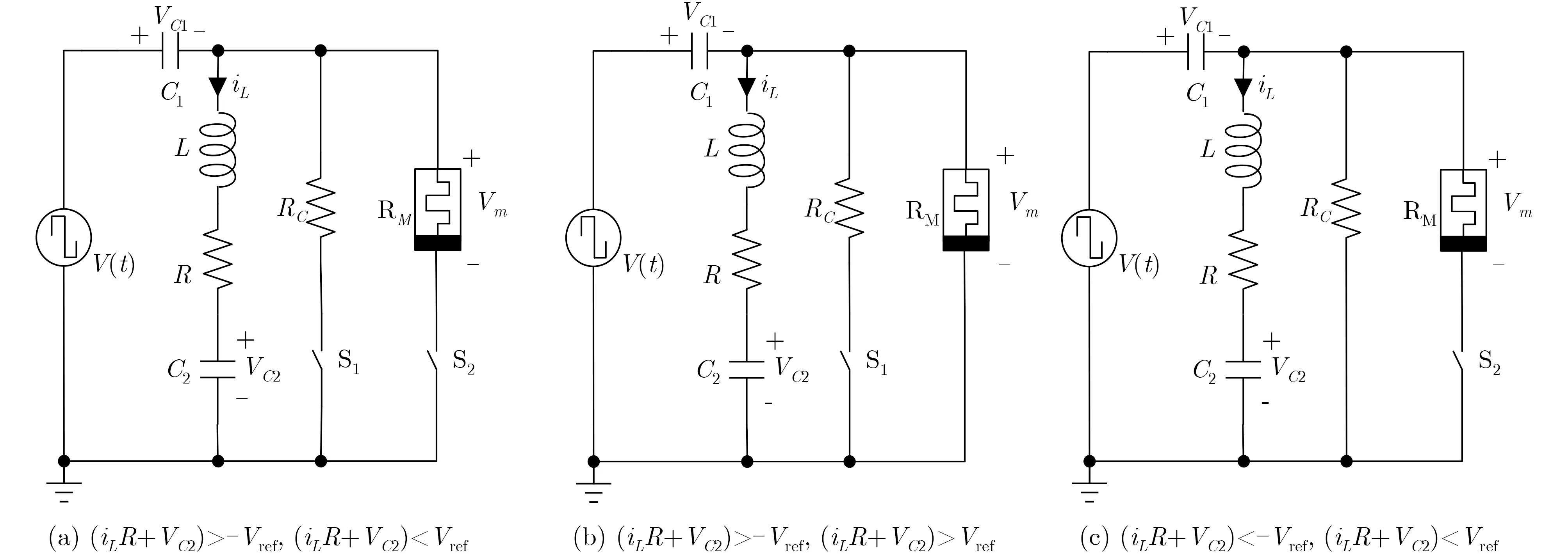
图3 开关电路的工作状态电路图
3 仿真实验
该电路数值仿真得到的时序波形如图4所示,当开关S1和开关S2断开时,即当电阻R与电容C2两端的电压之和大于-Vref且小于Vref时,比较器U1和比较器U2的输出端输出为零,电路没有达到发生边界碰撞的条件,此时系统仿真时序波形图如图4(a)所示,系统的运行状态是周期的。可以注意到其中VU1和VU2始终为0 值,即S1与S2始终保持为断开的状态,此时电路工作模式拓扑图始终为图3(a)所示。当开关S1或开关S2被导通时,即当电阻R与电容C2两端的电压之和小于-Vref或者大于Vref时,比较器的U1和U2的输出端输出不全为零,此时电路工作模式在图3(a),图3(b),图3(c)3种电路模式下转变。当输入电压V(t)的电压峰值小于3.29 V时,其数值仿真得到的时序波形图如图4(b)所示,VU1和VU2在0与1值之间无序跳变,此时系统的工作状态处于混沌态。当输入电压V(t)的电压峰值大于3.7 V时,依据电路初值状态的不同,电路的时序波形图分别如图4(c)、图4(d)、图4(e)所示,开关S1和开关S2被有序导通,此时系统中存在几种不同的周期极限环共存。当V(t)的电压峰值等于3.7 V时,系统中发生了边界碰撞,在V(t)的电压峰值大于3.7 V时,依据系统初始状态的不同,系统的运行轨迹也改变,这表明在V(t)的电压峰值等于3.7 V时系统中出现了边界碰撞分岔。
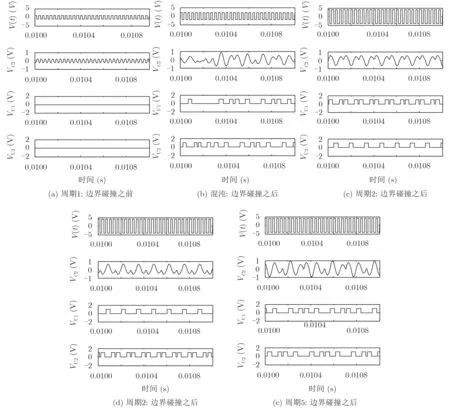
图4 电路时序波形图
当系统的参数固定,各参数的初始状态发生变化时,系统的运作轨迹也改变并形成不同的混沌吸引子,从而形成了多吸引子共存现象。选择系统参数为a=50,b=5000,c=d=1×109,f=1/30,h=1/3×108,m=n=50000。用Ep表示参数E的正值,当Ep增大时,该忆阻分段光滑系统状态变量Z的分岔图如图5所示。图5为共存分岔图,其中红色部分对应系统初始状态为(0, 0, 0, -1)、蓝色部分对应系统初始状态为(0, 0, 1, -1)、绿色部分对应系统初始状态为(1, 1, 1, -1);从 图5可以看出,系统呈现了不同周期数的极限环共存、周期与混沌吸引子共存等复杂的动力学行为。
如图5所示,当Ep<0.28时,系统中存在3个单周期极限环的共存。从图中可以看出当选取系统初始值为(1, 1, 1, -1)时,系统的运行轨迹在Ep>0.28后开始变得不稳定,在两种单周期极限环之间跳变。随着Ep的增大,在Ep=0.38,选取系统初始值为(0, 0, 0, -1)时,系统的运行轨迹也开始在两种单周期极限环之间跳变。这种状态持续到Ep=0.74时,系统发生边界碰撞,两种系统运行轨迹都进入了混沌态,此时系统中存在混沌态和单周期状态的共存。当Ep=1.4时,系统发生边界碰撞由原来的周期1极限环进入混沌态。此时系统运行状态为混沌态,系统具有良好的混沌鲁棒性,一直持续到Ep=3.28时,系统由混沌态开始过渡到周期态。在3.28

图5 状态变量Z随参数E变化的系统共存分岔图
图6给出了随系统参数E变化时,系统的XZ平面相轨图,从此图可以看出,在E相同而电容、电感、忆阻器的初始条件不同的情况下、系统产生了不同的共存吸引子。
当E=±0.34时,系统的X-Z平面相轨图如图6(a)所示,存在3种单周期极限环共存。其中红色部分、蓝色部分和绿色部分所对应的系统初始值分别为(0,0,0,-1),(0,0,1,-1)和(1,1,1,-1)。当E=±1时,系统的X-Z平面相轨图如图6(b)所示,其中绿色部分与蓝色部分的混沌吸引子重叠,可以看到系统中存在单周期与混沌吸引子的共存。当E=±3.28时,系统的X-Z平面相轨图如图6(c)所示,系统中存在两种不同的混沌吸引子共存现象。当E=±3.4时,系统的X-Z平面相轨图如图6(d)所示,系统中存在两种上下对称的双周期极限环共存。当E=±4时,系统进入了稳定的周期态,系统的X-Z平面相轨图如图6(e)所示,系统中存在上下对称的双周期极限环和5周期极限环共存。
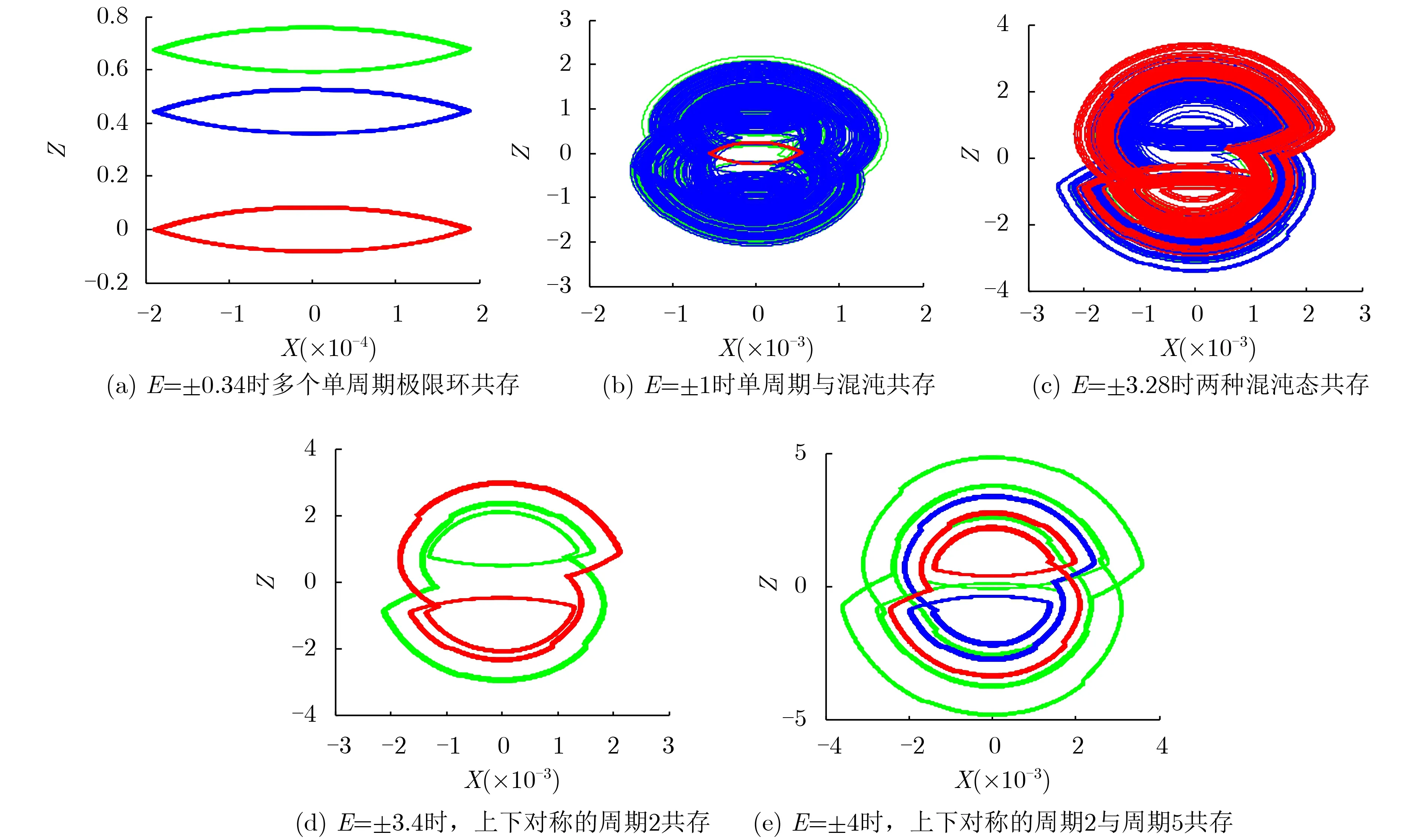
图6 随参数E变化的X-Z相轨图
4 电路仿真
采用PSIM电路仿真软件对图1所示电路进行电路模拟仿真,进一步验证其动力学特性,其模拟电路仿真原理图如图7所示。其中方波电压源的频率为30 kHz,占空比为50%,p为乘法器M2的比例因子,其他电路元件参数如表1所示。实验得到的电路时序波形如图8所示,对应得到的关于电感iL与电压VC2的相图如图9所示。
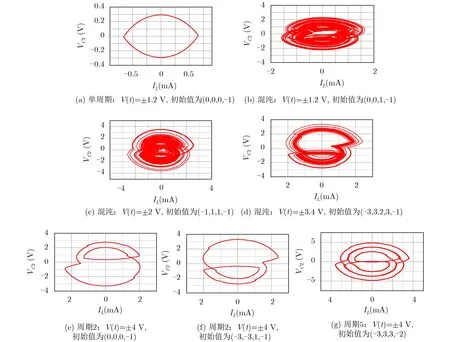
图9 电路的PSIM仿真相图
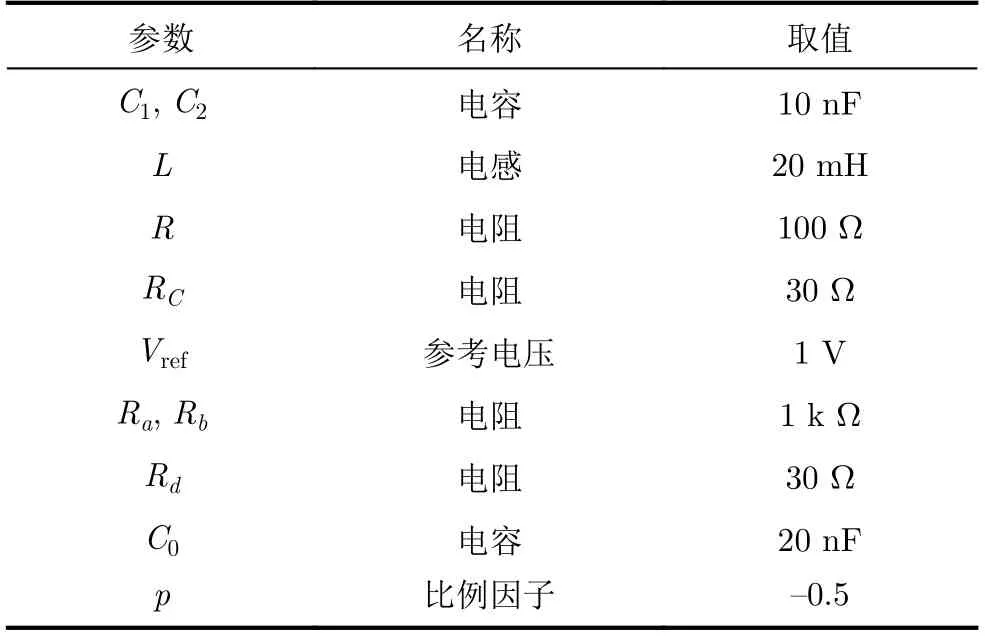
表1 忆阻开关混沌电路的参数选取
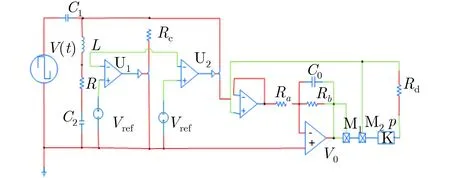
图7 PSIM仿真电路原理图
如图8(a)所示,当V(t)=±1.2 V电路参数的初始值为(0,0,0,-1)时,电阻R和电容C2两端的电压值之和没有达到参考电压Vref和-Vref,此时比较器的输出持续为零,开关S1和开关S2始终没有被导通,电路工作在1个周期1的极限环状态下。当V(t)不变,电路参数的初始值为(0,0,1,-1)时,如图8(b)所示,电阻R和电容C2两端的电压值之和在运行过程中达到了参考电压Vref和-Vref,比较器U1和U2输出端输出无序的高低电平,电路工作状态为混沌态。这两种状态在V(t)=±1.2 V时在系统中共存。图8(c)为当V(t)=±2 V时的电路时序图,图8(d)为当V(t)=±3.4 V时的电路时序图,可以看出此时开关S1和开关S2也是无序的导通,电路工作在混沌态。图8(e)和图8(f)分别为当V(t)=±4 V时的两种周期2态,如图8(e)所示,每两个周期,开关S1被导通两次,开关S2被导通一次。而图8(f)正好与之相反,每两个周期,开关S1被导通1次,开关S2被导通2次。图8(g)为当V(t)=±4 V时的另一种情况,每5个周期,开关S1被导通4次,开关S2被导通3次。在V(t)=±4 V时,这3种状态在系统中共存。当电路中存在噪声时,这几个吸引子之间很容易互相切换。
相图如图9所示,其中IL表示流过配电感的电流,VC2表示电容C2两端的电压。图9(a)为V(t)=±1.2 V时对应的单周期相图。图9(b)为V(t)=±1.2 V时对应的混沌态的相图。可以看出在V(t)=±1.2 V时,系统中存在单周期与混沌态的共存。当V(t)=±2 V时,系统相图如图9(c)所示,系统工作在混沌态且随着V(t)在1.4 V时发生边界碰撞,此时电路工作的混沌态与V(t)=±1.4 V之前的混沌态不同,此时系统具有良好的混沌鲁棒性。在V(t)=±3.4 V时,系统中还存在图9(d)所示混沌态与图9(c)所示混沌态共存。在V(t)=±4 V时得到图9(e)、图9(f)、图9(g)的系统相图,可以看出此时电路中存在上下对称的周期2与周期极限环的共存。
5 结束语
本文构建了一个具有多吸引子共存现象的忆阻开关电路,并将其建模为分段光滑的数学模型,进行了Matlab数值仿真和PSIM电路仿真,其结果表明,当电路中出现边界碰撞时有可能导致系统中出现多吸引子分岔现象,在分岔点之后系统中可能出现不同形式的混沌吸引子共存,不同形式的周期极限环共存等现象。实验验证了在开关电路中出现的多吸引子分岔现象,进一步推进了开关电路在混沌系统中的应用。此外,所构造的忆阻开关混沌电路其电路结构较为简单,相比于一般的混沌电路,该电路的动力学行为更加复杂,在随机数的产生、混沌保密通信、图像加密中具有潜在的应用价值。