无人机基站的飞行路线在线优化设计
2022-01-04张广驰严雨琳
张广驰 严雨琳 崔 苗* 陈 伟 张 景
①(广东工业大学信息工程学院 广州 510006)
②(广东省环境地质勘查院 广州 510080)
③(中国电子科学研究院 北京 100043)
1 引言
在过去的十年中,由于无人机(Unmanned Aerial Vehicle, UAV)移动性高、成本低等特点,无人机在无线通信领域引起了广泛的关注[1]。无人机在即将到来的5G通信时代也会发挥重要的作用,主要可以分为两类。第1类,无人机可以作为空中移动的通信平台辅助地面基站的通信。无人机基站可以为超密集网络的地面基站提供补充覆盖,也可以利用空地信道增益大的优势为毫米波通信提供高增益的无线连接。在应对自然灾害紧急救援情况时,无人机基站可以临时代替被损坏的地面基站提供应急通信。在基础设施覆盖不足的地区,无人机基站可以作为中继为地面用户提供无线通信服务。在热点区域或者需要处理临时事件期间,无人机基站能够为网络流量拥塞的地面基站提供有效的业务分流。第2类,无人机作为空中的用户,接入到地面的蜂窝通信网络。未来5G蜂窝网络能够为无人机提供更加可靠、更加安全和超低时延的连接从而实现其更多功能[2-6]。文献[3]研究了无人机通信网络中物理层安全性的问题;文献[4]研究了多无人机基站通信网络中的轨迹优化和功率分配问题;文献[5]研究了无人机中继系统中通过轨迹优化和功率分配来最大化吞吐量的问题。
本文主要研究的是上述第1类应用场景,即无人机作为空中基站为地面用户提供无线通信服务。相比于传统的地面基站,无人机基站的飞行高度比较高,能够与用户建立更加可靠的通信链路[4],能够适应突发情况下的通信场景,例如救援、搜索、热点区域覆盖等。目前大多数的研究是通过优化无人机的位置部署、无人机的飞行轨迹或者资源分配来达到更佳的通信质量。例如文献[7]研究了最小化无人机基站的数量以及部署无人机的位置来覆盖给定数量的地面用户;文献[8]研究了无人机辅助的无线传感网中的数据采集;文献[9]研究了多跳无人机中继通信系统的轨迹优化以及功率分配。上述文献中采用的算法都属于离线优化算法,建立在对通信环境的完美假设的基础上,在无人机起飞之前规划好无人机的轨迹。然而在实际中,通信环境是不断变化的,无法提前预测,通信环境的完美假设无法实现[10],因此无法解决地面用户随机的通信请求问题。与离线优化算法不同,在线优化算法不需要在无人机起飞前提前设计好无人机的飞行路线,而是能够在飞行过程中根据通信环境的变化动态、连续地规划无人机的飞行路线。文献[11]提出了一种近似动态规划的无人机机动决策方法;文献[12]提出一种基于动态规划的在线优化算法,而动态规划需要一个环境模型,且计算复杂度较高。
为了让无人机基站具有动态、实时规划飞行路线的能力,从而实现飞行路线能够实时适应地面用户随机的通信请求,并且考虑到无人机基站与地面用户进行时效性较强的决策信息通信时,减小通信时延尤为重要。本文将从平均通信时延最小化的角度出发,提出基于强化学习的飞行路线在线优化设计算法。在线优化算法能够在飞行过程中根据通信环境的变化动态地规划无人机的飞行路线,不需要完备的通信环境参数且计算复杂度比动态规划的低。强化学习方法包含蒙特卡罗和Q-Learning两类算法,用于解决马尔可夫决策问题[13]。实践证明,强化学习算法具有解决无人机无线网络在线优化问题的能力,例如文献[14]研究了多无人机辅助蜂窝网络中的用户体验质量(Quality of Experience,QoE);文献[15]研究了多无人机辅助蜂窝网络中所有用户的通信速率和最大化的问题。
本文研究一个无人机空中基站为两个地面用户提供无线通信服务,其中地面用户的通信请求是随机的,以平均通信时延最小化为目的来设计无人机的在线飞行路线。首先,把飞行路线设计问题转化成一个马尔可夫决策过程,根据地面用户的通信请求情况和无人机的位置把无人机的状态分为通信状态和等待状态,然后定义不同状态下的动作集,将无人机完成单次任务的通信时延设置为回报,采用强化学习的蒙特卡罗算法以及Q-Learning算法实现在线优化无人机飞行路线。最后,通过计算机仿真验证本文提出的算法的有效性。
2 系统模型
如图1所示,本文考虑一个无人机基站通信系统,其中包括有一个无人机和两个地面用户1)本文主要研究无人机基站的飞行路线在线优化,主要考察飞行路线对通信性能的影响,没有考虑无人机基站的能耗问题。另外,本文考虑的系统模型同样适用于多个无人机基站分别在不同频段上与地面用户通信的场景,并且后文提到的优化算法可以直接扩展到多个地面用户处在一条直线上的场景。。无人机作为一个空中通信基站,为两个地面用户提供无线通信服务。假定两个地面用户的通信请求是随机的,它们独立同分布,服从均值为λ/2的泊松过程(λ/2次请求/秒),每次通信请求的传输信息量为Lbit,地面用户1位置坐标为(−a,0,0)和地面用户2的位置坐标(a,0,0)。假设无人机的飞行高度固定为H,最大飞行速度为Vmax,无人机在两个地面用户所连接的线段间移动。定义无人机单次完成传输任务的时间为T,称为单次通信时延,在时刻t无人机的位置坐标为q(t)=(x(t),y(t),H),x(t)∈[−a,a],y(t)=0。因为地面用户的位置都在X轴上,无人机为了获得更好的通信链路需要尽可能靠近地面用户,所以无人机的飞行路线也在X轴。

图1 无人机基站通信系统
无人机收到地面用户r ∈{1,2}的通信请求之后,进入通信状态,此时无人机为地面用户提供无线通信服务,其他地面用户的通信请求会被忽略。在完成数据传输之后,无人机进入等待状态,开始等待下一次通信请求,这个过程一直重复。
由于无人机的飞行高度比较高,与地面用户的链路与视距信道相似,所以本文假设无人机与地面用户之间的通信链路为视距信道[16],无人机的发射功率固定为P,在t时刻,无人机与地面用户之间的瞬时通信速率为

3 飞行路线在线优化设计算法
3.1 问题描述

其中,q′(t)表示无人机的速度V。式(2a)是保证在第m次通信任务中,Tm时间内能够传输Lbit的信息;式(2b)表示无人机的飞行速度的约束,无人机的速度可取0或者Vmax;式(2c)是对无人机的位置约束。很明显(P1)是一个非凸的问题,同时为了让无人机基站具有动态、实时规划飞行路线的能力,从而适应不可预测、随机的地面用户通信请求,所以本文提出无人机飞行路线在线优化设计算法。所提算法基于强化学习的思想。
3.2 强化学习概述

将(P1)问题中无人机的轨迹离散化重新表述成一个马尔可夫决策过程。(P1)对应的马尔可夫决策过程如下:



3.3 最小单次通信时延

很明显lp1,p2=lp2,p1,lp1,p2=l−p1,−p2。
接下来证明单次通信时延最小的飞行路线的存在,假设无人机与地面用户1通信,对于任意一条轨迹q(·)∈A1(qi →qj),时延为Δt,可以找到另外一条轨迹q^(·)∈A1(qi →qj),时延同为Δt,满足|q(t)−x1|≥|q^(t)−x1|,∀t ∈[0,Δt],无人机在q^(·)轨迹下总是比在q(·)轨迹下更靠近地面用户1。因此在相同通信时延的情况下,无人机在q^(·)轨迹下总是比在q(·)轨迹下能够传输更大的信息量。换句话说,当无人机的通信状态的起始位置和结束位置相同时,q^(·)更靠近地面用户1,获得更好的通信链路,从而减小通信时延。同理,无人机与地面用户2通信的情况相同。

3.4 基于蒙特卡罗的在线优化设计算法
蒙特卡罗算法通过平均样本的回报来解决强化学习问题。为了保证能够具有良好定义的回报,本文采用用于分幕式任务的蒙特卡罗算法。智能体与环境的交互分成一系列子序列,将子序列称为幕,每幕从某个标准起始状态开始,并且无论选取怎样的动作整个幕一定会终止,下一幕的开始状态与上一幕的结束方式完全无关,具有这种分幕特性重复任务称为分幕式任务。价值估计和策略改进在整个幕结束之后进行,因此蒙特卡罗算法是逐幕做出改进的。蒙特卡罗算法是从任意的策略π0开始交替进行完整的策略评估和策略改进,最终得到最优的策略和动作价值函数。策略评估的目标是估计动作价值函数Qπ(s,a),即在策略π下从状态s采取动作a的期望回报。策略改进是在当前的动作价值函数上贪婪地选择动作。由于已经存在动作价值函数,所以在贪婪的时候完全不需要使用任何的模型信息。对于任意的一个动作价值函数,对于任意的贪婪策略为:对于任意一个状态s ∈S,必定选择对应动作价值函数最大的动作,π(s)=arg maxaQ(s,a)[13]。在每一幕结束后,使用观测到的回报进行策略评估,然后在该幕序列访问到的每一个状态上进行策略的改进。本文采用的是基于试探性出发的蒙特卡罗算法,具体算法如下:
步骤1 初始化最大训练幕数Nepi,每幕中最大步数Nstep,对于所有s ∈Scomm,任意初始化;对于所有s ∈Scomm,a ∈A∗r(qi)任意初始化动作值函数Q(s,a)∈R;
步骤2 随机选择s0=(i,r),根据π生成一幕序列:s0,a0,R1,s1.a1,...,sNstep−1.aNstep−1,RNstep;
步骤3G=0;计数变量W=0;Nepi=Nepi−1;
步骤4 对幕中的每一步循环,n=Nstep−1,Nstep−2,...,0:
文献报道显示绝大多数神经系统的症状和体征是一过性的,于数周或数月可完全恢复[8]。但脂肪栓塞综合征治疗成功的关键在于早期诊断、综合对症支持治疗。尚无特异性溶脂治疗方法,主要是对肺、脑等器官的保护。目前通过(1)骨折部位的早期固定及固定方式的改变[2];(2)预防性使用激素来减少脂肪栓塞综合征的发生。甲泼尼龙是目前最常使用的激素,剂量范围为 6~90 mg/kg[1,9]。

当二元组sn,an在s0.a0,s1.a1,...,sNstep−1.aNstep−1中出现过,退出幕中循环。
步骤5 重复步骤2-步骤4,直到Nepi=0。
3.5 基于Q-Learning的在线优化设计算法
与前面提到的蒙特卡罗算法一样,时序差分算法也可以直接从环境互动的经验中学习策略。时序差分算法与蒙特卡罗方法不同,不用等到交互的最终结果,而是在已得到的其他的状态估计值来更新当前状态的价值函数,其价值估计和策略改进是逐步的。与蒙特卡罗算法相比,时序差分算法的优势在于它运用了一种在线的、完全递增的方法来实现。蒙特卡罗算法必须等到一幕的结束才能知道确切的回报值,而时序差分算法只要等到下一时刻即可[13]。因为本文系统模型中的地面用户的通信请求是逐个发送的,然后由无人机逐个完成的,所以采用时序差分算法更加适合。本文采用的Q-Learning是一种典型的强化学习时序差分算法,动作价值函数定义为Q(sn,an)=Q(sn,an)+α[rn+1+γmaxaQ(sn+1,a)−Q(sn,an)],其中α ∈(0,1]为步长,权衡上一次学习的结果和这一次学习的结果;γ ∈[0,1]为折扣率,是考虑未来回报对现在影响的因子,γ的值越大,说明未来回报对现在影响越大;具体如下:
步骤1 初始化探索参数ε,最大训练幕数Nepi,每幕中最大步数Nstep,动作价值函数Q(s,a)=0,∀s ∈Scomm,∀a ∈A∗r(qi);
步骤2 随机给定初始状态s0=(i,r);
步骤3Nepi=Nepi−1;
步骤4 对幕中的每一步循环,n=1,2,...,Nstep:

更新动作价值函数,Q(sn,an)=Q(sn,an)+α[rn+1+γmaxaQ(sn+1,a)−Q(sn,an)];
步骤5 重复步骤2-步骤4,直到Nepi=0。
4 仿真结果
本节利用计算机仿真对上述所提的飞行路线在线优化算法进行验证,并对比两种基准方案“固定位置”和“贪婪算法”。“固定位置”为无人机悬停在两个地面用户的连线的中点,“贪婪算法”的描述为在无人机每次进入通信状态(i,r)时,选择最小单次通信时延的飞行路线,即通信状态的结束位置qj。
仿真中采用的系统参数为:地面用户1和地面用户2相距800 m,其中地面用户1的位置坐标为(−400 m,0,0),地面用户2的位置坐标(400 m,0,0);两个地面用户的通信请求到达率λ=1 次/秒,传输的信息量L=2 Mbit,无人机的飞行高度H=100 m,最大飞行速度Vmax=20 m/s,信道带宽B=1 MHz,参考距离1 m时的信噪比γdB=40 dB。将无人机的可飞行区域分为2N+1=101个位置状态,其他参数:Nepi=120,Nstep=10000,ε=0.1,α=1,γ=0.2。


图2 等待状态时采取不同动作策略的平均通信时延

在以下的仿真中,无人机的等待状态都采取等待状态动作策略2。
图3展示了不同算法下的无人机平均通信时延,可以看出相比于“固定位置”,其他3种算法下的平均通信时延都比较小,其中基于Q-Learning的在线优化设计算法的平均通信时延最小。这是因为“贪婪算法”只考虑当前的回报,没考虑长期回报;而蒙特卡罗算法把学习推迟到整幕结束之后,必须等到每一幕的结束,才能知道确切的回报值,而Q-Learning算法在每个动作结束就能够知道回报值从而进行学习,本文中的问题是一个持续性任务,不适合分幕式任务的蒙特卡罗算法,更加适合用Q-Learning算法来解决。

图3 不同算法下的无人机平均通信时延
图4展示在不同的传输信息量下,采用不同算法得到的平均通信时延。可以看出基于Q-Learning的在线优化设计算法的平均通信时延始终优于基于蒙特卡罗算法和“贪婪算法”的在线优化设计算法。传输信息量越大,基于Q-Learning的在线优化设计算法的时延性能越好。

图4 不同传输信息量以及不同算法下的无人机平均通信时延
图5展示了基于Q-Learning的在线优化设计算法和基于蒙特卡罗算法的在线优化设计算法下的平均通信时延随着训练幕数增大而逐渐收敛,可以看出基于Q-Learning的在线优化设计算法要比基于蒙特卡罗算法收敛得更快且稳定。

图5 不同算法的收敛程度
图6和图7分别展示了基于Q-Learning算法和基于蒙特卡罗算法的在线优化设计算法下无人机连续的10个状态下的飞行路线,其中无人机的起点是随机的,无人机的状态是根据地面用户的通信请求变化的,两个地面用户通信请求分别服从均值为1/2的泊松过程。图6和图7中的无人机状态:0表示无人机处于等待状态,1表示接收到地面用户1的通信请求,2表示接收到地面用户2的通信请求;时长表示无人机处于当前状态采取的动作所耗费的时间。可以对比看出基于Q-Learning的在线优化设计算法的无人机飞行路线更加集中于两个地面用户的中点,说明基于Q-Learning的在线优化设计算法更加能适应随机的地面用户请求,从而得到更小的平均通信时延。
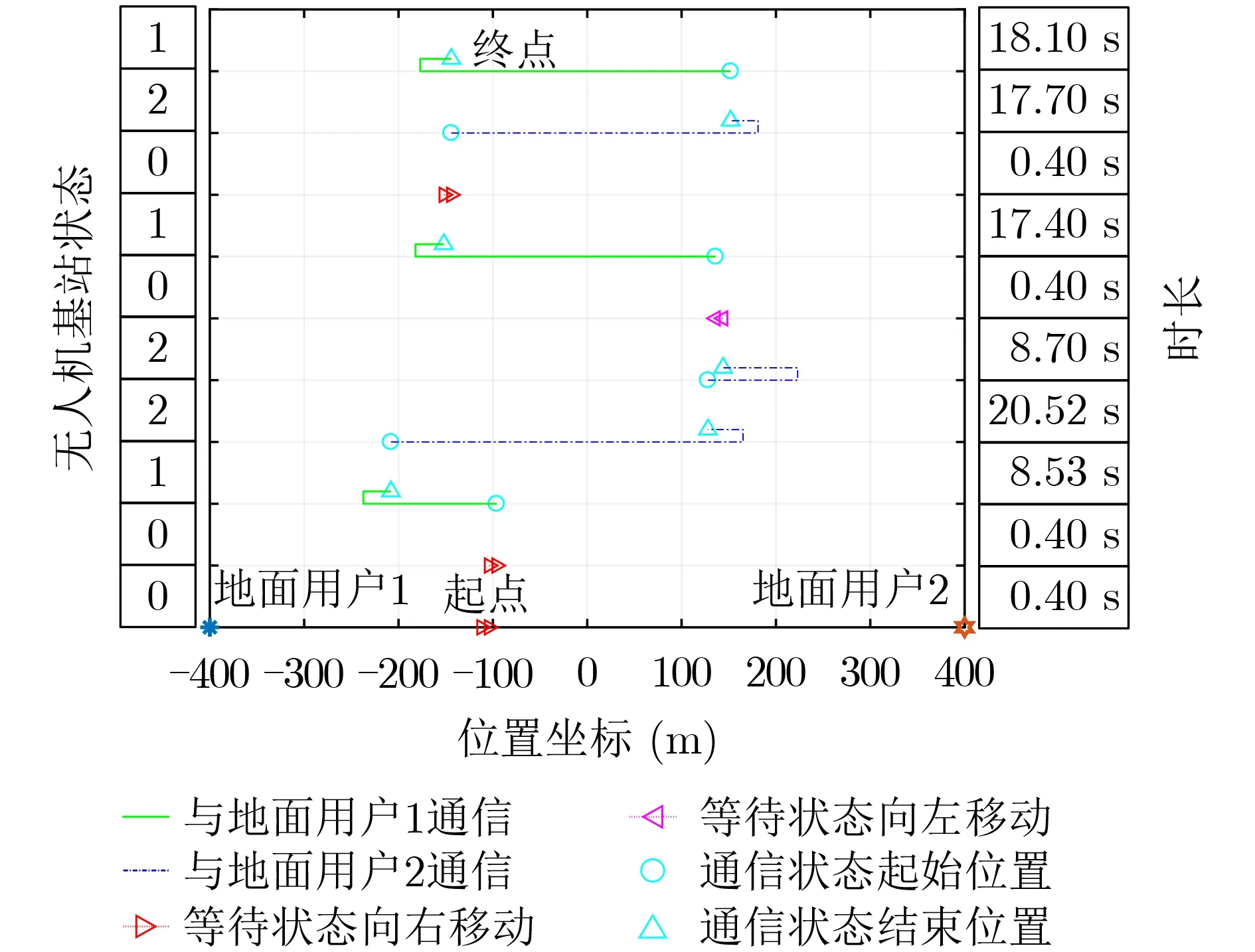
图6 基于Q-Learning的在线优化设计算法下无人机飞行路线
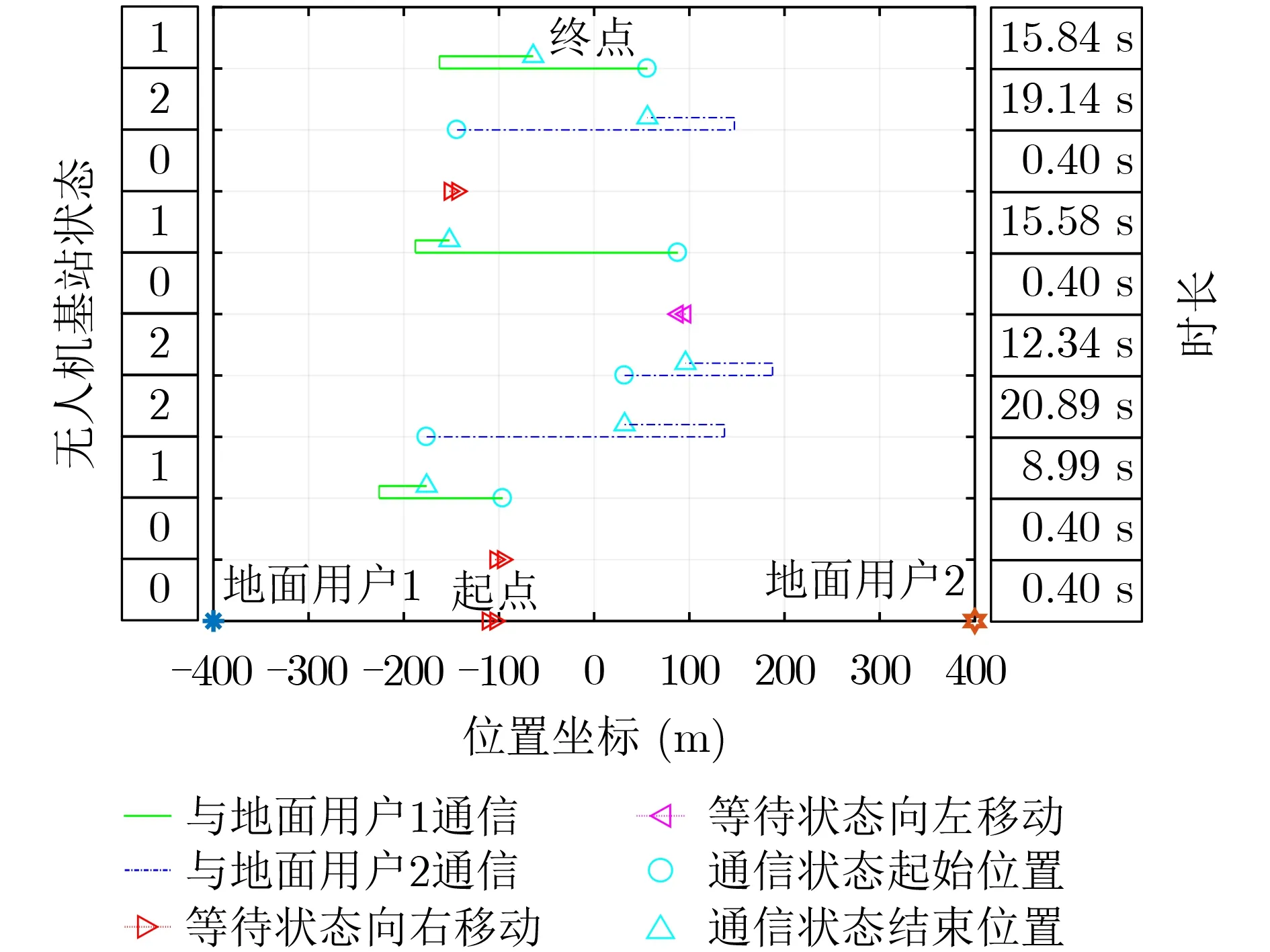
图7 基于蒙特卡罗的在线优化设计算法下无人机飞行路线
5 结束语
本文针对无人机基站通信系统,提出了两种基于强化学习的无人机飞行路线在线优化设计算法。分别采用了强化学习的蒙特卡罗算法和Q-Learning算法来最小化无人机的平均通信时延。仿真结果显示了与无人机在固定位置相比,提出的算法具有较好的性能。基于Q-Learning的在线优化设计算法比基于蒙特卡罗的在线优化设计算法的训练结果更快收敛且稳定,能够更好地适应随机的地面用户请求从而达到更小的平均通信时延。