不同载荷条件下的可靠性转换方法

傅惠民， 付越帅， 吴 琼

（1.北京航空航天大学小样本技术研究中心， 北京 100191； 2.北京空间飞行器总体设计部， 北京 100094）

0 引言

产品可靠性不但与原材料、设计、制造等有关，而且还与使用中遇到的载荷条件（包括环境条件）有关，同一类型产品在实际使用过程中遇到的载荷往往是多种多样的，有的差别很大[1-2]。 由于产品可靠性试验时间长、费用高， 所以工程上通常只能在一种典型载荷条件下进行试验，给出该典型载荷条件下的产品可靠度或可靠寿命。但是无论是厂家还是用户都希望了解和掌握产品在使用载荷条件下的可靠性。 为此，文献[3-5]建立了可靠寿命消耗评估和寿命管理方法， 本文进一步提出一种不同载荷条件下的可靠性转换方法， 能够将试验载荷下产品的可靠度和可靠寿命转换为实际使用载荷条件下的可靠度和可靠寿命，解决了上述难题。

1 单应力下的可靠性转换方法

载荷并不完全一致，加上实际使用载荷又是多种多样，为了获得产品在实际使用载荷下的可靠度和可靠寿命，下面给出一种不同载荷条件下的可靠性转换方法。

1.1 不同程序块谱下的可靠寿命转换方法

若产品实际使用载荷是由应力水平Si，i=1，2，…，q，组成的程序块谱，各应力水平加载时长为ni，则在该使用载荷谱下产品置信水平为γ、 可靠度为R 的可靠寿命单侧置信下限NRL由下式给出

1.2 不同载荷条件下的可靠度转换方法

若产品在应力水平为Si，加载时长为ni，i=1，2，…，q，的程序块谱下，工作了Nt次循环（以程序块谱为单位），则可通过求解下式

得到满足式（3）的可靠度，根据置信限曲线等同性原理可知，此可靠度即为产品在该载荷谱下经过Nt次循环时，其置信水平为γ 的可靠度R（Nt）单侧置信下限RL（Nt）。

对于一般情况，设截至某一时刻t，产品在应力水平Si下的工作时长为ni，i=1，2，…，m，则可通过求解下式

得到满足式（4）的可靠度，此即为产品在该使用载荷条件和工作时长下置信水平为γ 的可靠度R（t）单侧置信下限RL（t）。

2 多应力下的可靠性转换方法

2.1 不同程序块谱下的可靠寿命转换

式中，τ 为试验载荷谱对使用载荷谱的加速系数。 根据可靠损伤相等的原则[3]，τ 由下式计算

2.2 不同载荷条件下的可靠度转换

若产品在组合应力水平为Sij，加载时长为nij，i=1，2，…，q1， j=1，2，…，q2，的程序块谱下，工作了Nt次循环（以程序块谱为单位），则可通过求解下式

得到满足式（7）的可靠度，此即为产品在该载荷谱下经过Nt次循环时，其置信水平为γ 的可靠度R（Nt）单侧置信下限RL（Nt）。

同样对于一般情况，设截至某一时刻t，产品在组合应力水平Sij下的工作时长为nij，i=1，2，…，m1， j=1，2，…，m2，则可通过求解下式

得到满足式（8）的可靠度，根据置信限曲线等同性原理可知， 此可靠度即为产品在该使用载荷条件和工作时长下置信水平为γ 的可靠度R（t）单侧置信下限RL（t）。

对于产品受到三个或三个以上应力类型联合作用的情况， 其不同载荷条件下的可靠性转换也可以同样处理。

3 单应力向双应力情况的可靠性转换方法

对于工程上难以进行多应力耦合试验或多应力耦合加速系数函数未知的情况，上述方法无法适用。 为此，下面进一步给出由单应力向多应力情况的可靠性转换方法。 首先，针对产品受两种类型应力作用的情况（如航空发动机叶片的疲劳和蠕变）进行讨论。

3.1 单应力向双应力的可靠寿命转换

3.2 单应力向双应力的可靠度转换

得到满足式（11）的可靠度，此即为产品在该使用载荷条件和工作时长下置信水平为γ 的可靠度R（t）单侧置信下限RL（t）。

4 单应力向多应力情况可靠性转换方法

对于产品受多种类型应力作用的一般情况， 给出单应力载荷条件向多应力载荷条件下的可靠性转换方法。

4.1 单应力向多应力的可靠寿命转换

4.2 单应力向多应力的可靠度转换

得到满足式（13）的可靠度，此可靠度即为产品在该载荷谱下经过Nt次循环时， 其置信水平为γ 的可靠度R（Nt）单侧置信下限RL（Nt）。

同样对于一般情况，设截至某一时刻t，产品在应力水平Sj（i）下的工作时长为nj（i），i=1，2，…，m，j=1，2，…，mi，则可通过求解下式

得到满足式（14）的可靠度，此即为产品在该使用载荷条件和工作时长下置信水平为γ 的可靠度R（t）单侧置信下限RL（t）。

5 算例

设某零部件的疲劳寿命服从两参数Weibull 分布，其中形状参数下限已知为α0=3.5。 现该零部件在表1 所示的程序块谱下进行加速寿命试验，试验数据列于表2。

表1 试验载荷中各级载荷大小Si*及循环数ni*

表2 零部件加速寿命试验数据（以程序块谱为单位）

若工程实际中该零部件在表3 所示的使用载荷谱下工作， 则需将上面试验载荷下的可靠性转换为该使用载荷谱下的可靠性。 现已知该零部件加速系数方程为

表3 使用载荷中各级载荷大小Si 及循环数ni

式中，NRL，1和NRL，2分别为该零部件在应力水平S1和S2下置信水平γ=0.95、可靠度R=0.999 的可靠寿命置信下限。

根据式（1）、式（2）和表1、表3 以及式（15）计算结果，可得该零部件在表3 所示的使用载荷谱下置信水平γ=0.95、可靠度R=0.999 的可靠寿命单侧置信下限NRL为

若该零部件在表3 所示载荷谱下工作了Nt=1200 个循环，则可根据式（3）求解得到此时对应的置信水平γ=0.95 的可靠度单侧置信下限为

进一步， 还可以给出该零部件在表3 所示载荷谱下的置信水平γ=0.95 的可靠度单侧置信下限曲线 （可靠度退化曲线）RL（Nt），见图1。

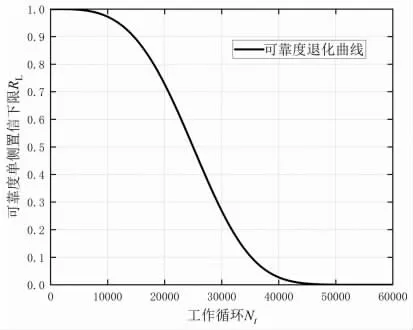
图1 可靠度单侧置信下限曲线

6 结论

提出一种不同载荷条件下的可靠性转换方法， 能够将试验载荷下产品的可靠度和可靠寿命转换为实际使用载荷条件下的可靠度和可靠寿命， 解决了目前采用试验载荷条件下的可靠度和可靠寿命来分析和评估实际使用情况下产品的可靠性而导致误差较大的问题。

针对工程上难以进行多应力耦合试验或多应力耦合加速系数函数未知的情况， 本文进一步建立了单应力向多应力情况的可靠性转换方法， 解决了其不同载荷条件下的可靠性转换问题。 而且这种基于多应力可靠损伤相加模型给出的可靠寿命和可靠度单侧置信下限通常偏于保守，工程上安全可用。此外，该方法可以节省大量试验，且计算简单，便于工程应用。