“月上柳梢头”的数学模型
2022-01-04唐纪芳
唐纪芳
(四川职业技术学院 教师教育学院,四川 遂宁 629000)
1 问题背景
“月上柳梢头,人约黄昏后”是北宋学者欧阳修的名句,写的是与佳人相约的情景.应用天文学的观点赏析该名句,并进行如下的讨论:
问题1:定义“月上柳梢头”时月亮在空中的角度和什么时间称为“黄昏后”.根据天文学的基本知识,在适当简化的基础上,建立数学模型,分别确定“月上柳梢头”和“人约黄昏后”发生的日期与时间.并根据已有的天文资料(如太阳和月亮在天空中的位置、日出日没时刻、月出月没时刻)验证所建模型的合理性.
问题2:根据所建立的模型,分析2016 年北京地区“月上柳梢头,人约黄昏后”发生的日期与时间.根据模型判断2016 年在哈尔滨、上海、广州、昆明、成都、乌鲁木齐是否能发生这一情景?如果能,请给出相应的日期与时间;如果不能,请给出原因.
2 模型假设
(1)设地球是一个标准的圆球体,那么它的半径就是地球的平均半径,记为r,即r=6378.004千米.这里忽略地球表面地形对计算带来的误差,仅仅是理论上的估算值.
(2)月亮绕地球旋转时,把月亮看成一个质点.假设月球绕地球匀速旋转,旋转轨迹为一个标准的圆.
(3)地球绕太阳转动时,因为相对运动,也可以看成太阳绕地球运动.
(4)假设忽略各种天气原因导致无法看到“月上柳梢头,人约黄昏后”的情况,如:雾霾,大雾,雪天,雨天等等.
3 符号说明
P:地球表面上任意一点,可以作为我们的观察点.
Π:过地球表面上任意一点P 的切平面.
μ(t):太阳直射点的经度;纬度为ν(t).
μ1(t):月亮直射点的经度;纬度为ν1(t).
x1(t):第t天的日出时间;日落的时间为x2(t).
y1(t):第t天的月出时间;月落的时间为y2(t).
4 模型的建立与求解
4.1 月上柳梢头的定义
月上柳梢头的景象,与诗人和柳树的高度及距离有着密切关系,但可以明确知道是在月出与月到天顶之间,角度约为15 度到30 度之间[1].由于一天中月出没的时间一般为12 小时,从月出到天顶为6 个小时,因此月上柳梢头定义为是月出后1 小时到两小时之间.
4.2 黄昏后的定义
传统的说法是此时太阳已经落山,天将黑未黑.天地昏黄,万物朦胧,故称黄昏.因此把每天日落后60 分钟这段时间称为黄昏.
4.3 问题分析
研究的问题为,一年中哪个月在满月(初十五)的时候,太阳已经落下的60 分钟之内,月亮已经升起了60 分钟以上.也即是满足“月上柳梢头,人约黄昏后”的时刻.
这就需要知道该天的月出时间与该天的日落时间.
以日作单位,记2015 年1 月1 日零时为初始时刻0,第t天的日出时间为x1(t),日落的时间为x2(t),月出的时间y1(t),月落的时间为y2(t).
4.4 问题 1 的解答
在某时刻,对站在地球上一点P的人,能看见苍穹中的星球A吗?过地球上一点P作出地球的切平面Π,若星球A与地球分别处在切平面Π 的两侧,在P点可以看见星球A.
若星球A刚好从Π 与地球为同侧而运动到Π上,该星球为刚好出来;若星球A刚好从Π 与地球为异侧而运动到Π 上,该星球为刚好离去,见图一.
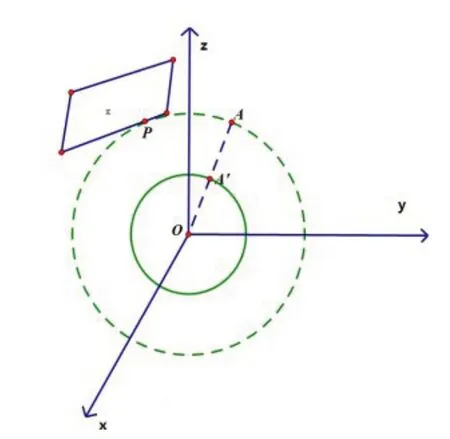
图一 观察点切平面
假设地球是一个标准的球体,半径为r,球心为O.地球上点P的经度为α,纬度为β.假设星球A为一个点,到地球球心的距离为R,在某时刻t(以日作单位,记2015 年1 月1 日零时为初始时刻0),星球与地心的连线通过地球表面上一点S,S叫做星球在地球的直射点,这点的地球经度为μ(t),纬度为ν(t).
知道α,β,就可以求出Π 的方程.知道了μ(t)与ν(t),就可以算出星球的位置坐标,某时刻t站在地球上点P,对看到或看不到星球A就可以做出准确的判断.
以地心O为原点,地球赤道平面为xOy平面,建立空间直角坐标系O-xyz,其中,x轴的正向过零度经线,z轴正向过北极. 地球上一点P的坐标为 (rcosβcosα,rcosβsinα,rsinβ),切平面 Π 的方程为[2]
xcosβcosα+ycosβsinα+zsinβ=r,其 中r=6378km.
问题的关键是求出星球A的直射点的地球经度μ(t),纬度ν(t).这就与星球A 的运动规律直接相关.
4.4.1 关于日出日落
(1)μ(t)的计算
各地的每天中午12 点正,太阳直射在通过该地的经线上,每过一小时,直射点西移的经度为15 度,以北京时间为准,在北京的中午12 点,太阳直射在通过北京的经线上,经度为116.4 度,故一天中北京时间s时,太阳直射在东经116.4 +15(s- 12) 度 上 ,即μ(t)= 116.4 + 15[12 -24(t- int(t))].
根据上述函数作出时间与太阳经度函数图,见图二.
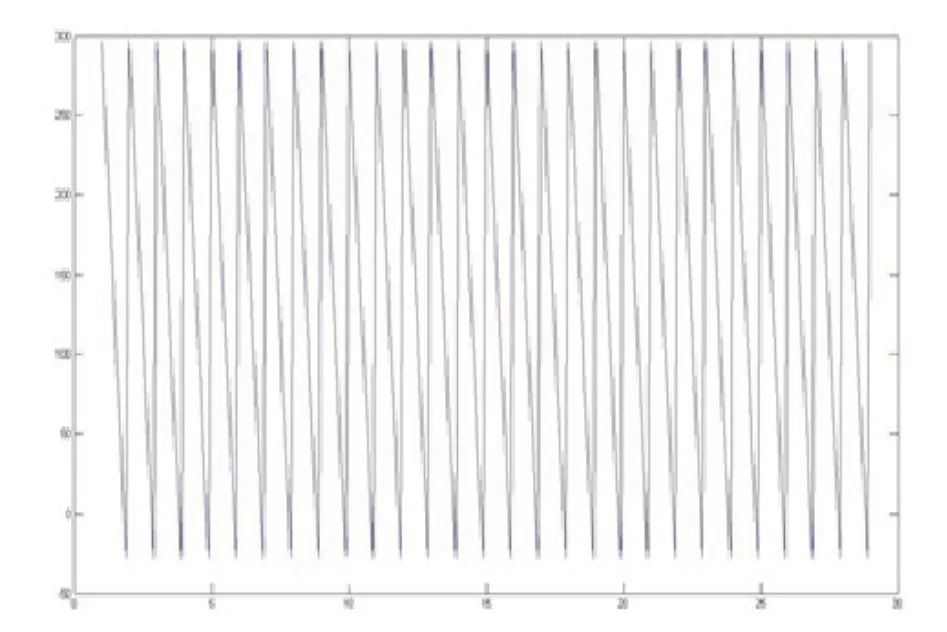
图二 太阳经度与时间函数图
由万年历,2015 年按北京时间的春分日期为3 月 21 日 6 点 45 分 ,此时 ,太阳直射地球赤道线上,直射点纬度为0 度.由于这时还差5 小时15 分才到中午12 点,故2015 年春分时,太阳直射在东经 195.15 度,即西经 164.85 度 .
(2)ν(t)的计算
通过田野作业理解和解读民众生活文化与意义世界,是当代民俗学的学术追求之一。研究者与叙述者(被研究者)共同完成该研究过程。同时,通过学术话语的灵活运用,研究者将叙述者的生活及叙事转译成为民俗志或民族志文本。因此,民俗学的实践主体应由叙述者与研究者共同构成,亦即在民俗研究中,研究者与叙述者是互为主体的平等协商关系,是民俗志或民族志作品的共同制作人,可以说,“我们都是故事生产过程中的一个重要环节”[注]黄盈盈:《作为方法的故事社会学——从性故事的讲述看“叙述”的陷阱与可能》,《开放时代》2018年第5期。。
由万年历,2015 年按北京时间的春分日期为3 月 21 日 6 点 45 分,t= 79.28,此时,太阳直射地球赤道线上,直射点纬度为0 度.
太阳直射点的纬度是从春分0°→23.5°→0°→ -23.5°→ 0°,即 春分 时ν(79.28)= 0,夏 至时ν(79.28)= 23.5,秋 分 时ν(79.28)= 0,冬 至 时ν(79.28)= 23.5,2016 年春 分 时ν(79.28)= 0. 在建立函数ν(t)时,分别试用了平均法、拟合法,均未能得到理想的效果,考虑到直射纬度的周期性,最后采用了便于计算的正弦型函数来建立[3].即
根据上述函数作出时间与太阳纬度呈正弦函数曲线,如图三.
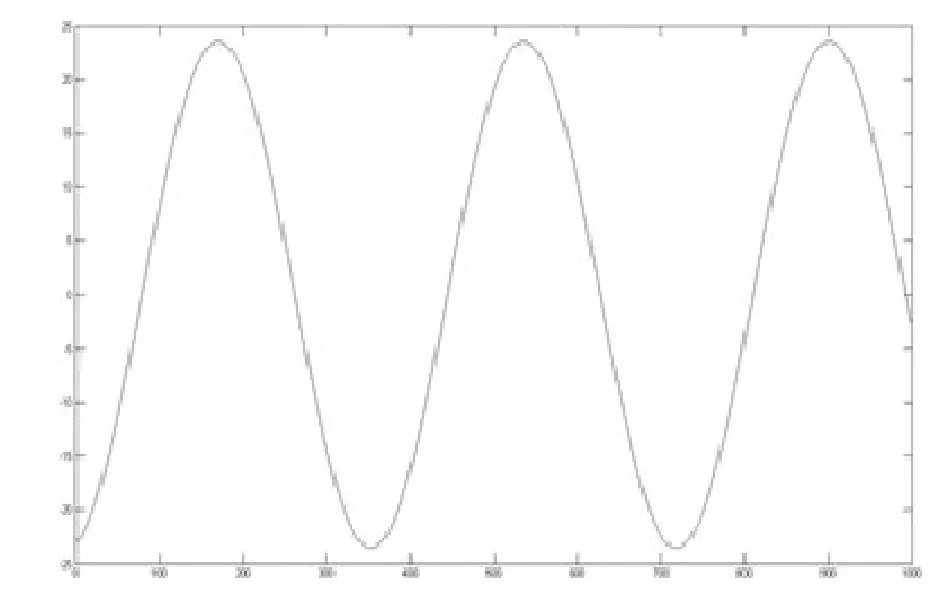
图三 太阳纬度与时间函数图
(3)计算日出日落时间
如果某时太阳直射线OS通过P点的切平面Π,则我们可以看见太阳.由于太阳距离地球特别远,易知向量的夹角不大于90 度[4],太阳直射线OS必定通过P点的切平面Π,那么cos∠POS≥0,可 知(cosβcosα,cosβsinα,sinβ)和
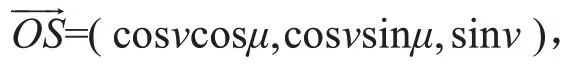
那么就有 cosβcosαcosμcosν+cosβsinαcosνsinμ+sinβsinν≥ 0,等于90 度时,则是日出日落的时刻,那么 cosβcosαcosμcosν+cosβsinαcosνsinμ+ sinβsinν=0.
通过计算,我们即可得到北京地区2015 年1月1 日至2016 年12 月31 日间人约黄昏后的时间表,见表1.(插表太阳落下随机选一部分)
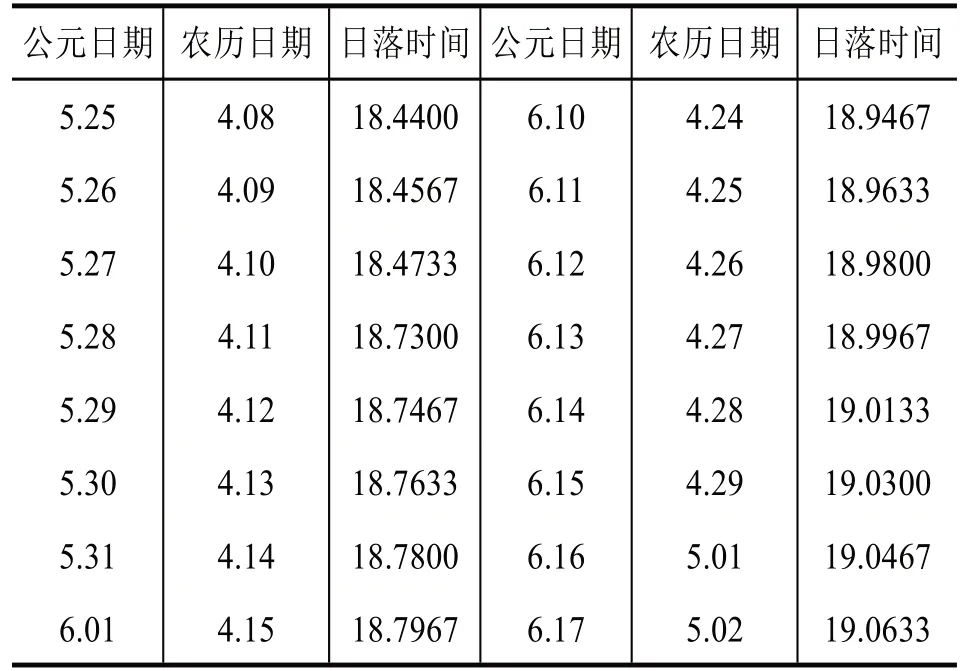
表1 人约黄昏后时间表
这与寿星天文历很吻合,说明我们的模型是比较正确的.
注:寿星天文历一款采用现代天文算法制作的农历历算程序.含有公历与回历信息,可以很方便的进行公、农、回三历之间的转换.提供公元-4712 年到公元9999 年的日期查询功能.
4.4.2 关于月出月落
(1)月球的直射点经度μ(t)的计算
由于地球自转一周,转过360°,但月亮绕地心公转的周期为29.530588 日,平均每天转= 12.19075 度.
由于2015 年5 月25.24 日月球在地球上的直射点的经度为98 度,纬度为0 度,我们即可得到月球的直射点经度计算式,即
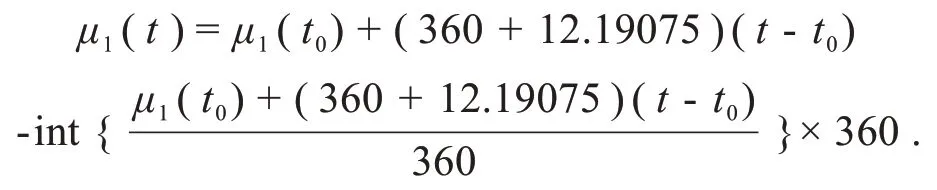
其中t0=2015 年 5 月 25.24 日 .
(2)月亮的纬度计算
由于月球的公转平面和地球的公转平面不重合(轨道圆心重合),有一个大约5 度9 分的夹角,月球的纬度从μ1(t0)= 0 开始,公转一周29.530 588 日 ,经 过 从 0°→ 5.15°→ 0°→ -5.15°→0°的变化过程,让我们联想到正弦型函数具有这样的周期性,故我们对月球在地球的直射点纬度有一个粗略的算法:即

(3)月出月落时刻的计算
由于月亮到地心的距离为地球半径的61 倍,那么我们看得见月亮时有
即 ∠POS≤89°, 故 有 cosβcosαcosμcosν+cosβsinαcosνsinμ+sinβsinν,那么月出月落的条件为:
cosβcosαcosμcosν+cosβsinαcosνsinμ+sinβsinν
我们运用上面的方法也可以得到2015 年1 月1 日至2016 年12 月31 日的北京地区的月出月落时刻,表2 随机选一部分月出时刻.
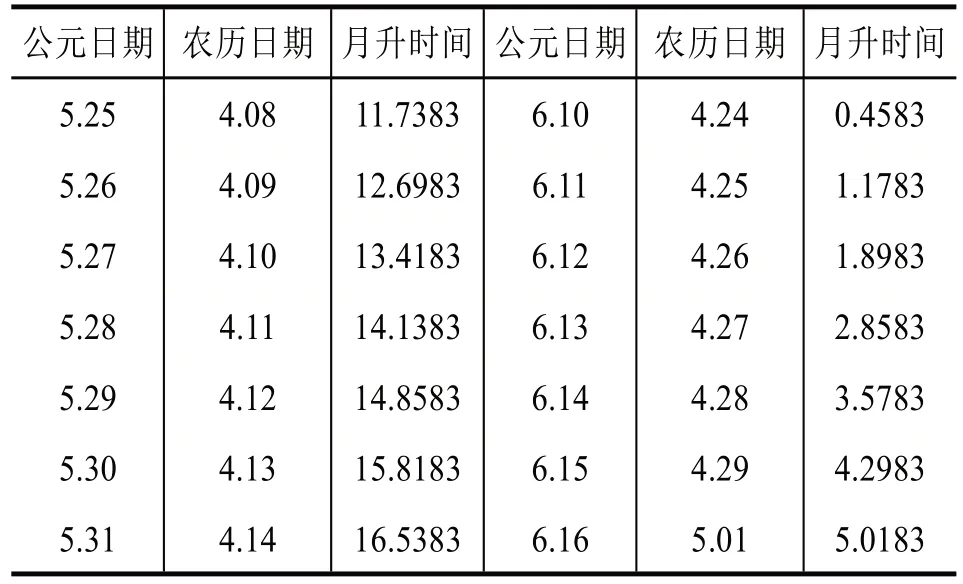
表2 月出月落时刻表
4.4.3 比较月升日落
根据年中哪个月在满月(初十五)的时候,太阳已经落下的60 分钟之内,月亮已经升起了60分钟以上.也即是满足“月上柳梢头,人约黄昏后”的时刻的定义.根据模型计算出符合“月上柳梢头,人约黄昏后”的时间(见表3).这与寿星天文历很吻合,说明此模型是比较正确的.

表3 符合“月上柳梢头,人约黄昏后”的时间
4.5 问题 2 的解答
月上柳梢头这个时候,太阳、地球、月亮几乎在一条直线上,地球在太阳和月亮之间,从地球上几乎可以完全看到月亮被太阳照亮的一面,就是满月.另外,根据欧阳修的诗中意境也可知为满月 .从 2016 年元月 1 日到 2016 年 12 月 31 日 ,当月正圆的时候,时间分别依次为为t1,t2,t3,…,t12,既满足月上柳梢头又满足人约黄昏后的条件为
x2(ti)≤y1(ti)+ 1 ≤y1(ti)+ 2 ≤x2(ti)+ 1(i=1,2,…,12).
我们通过比较,得出2016 年各地满足“月上柳梢头,人约黄昏后”的情况,见表4.
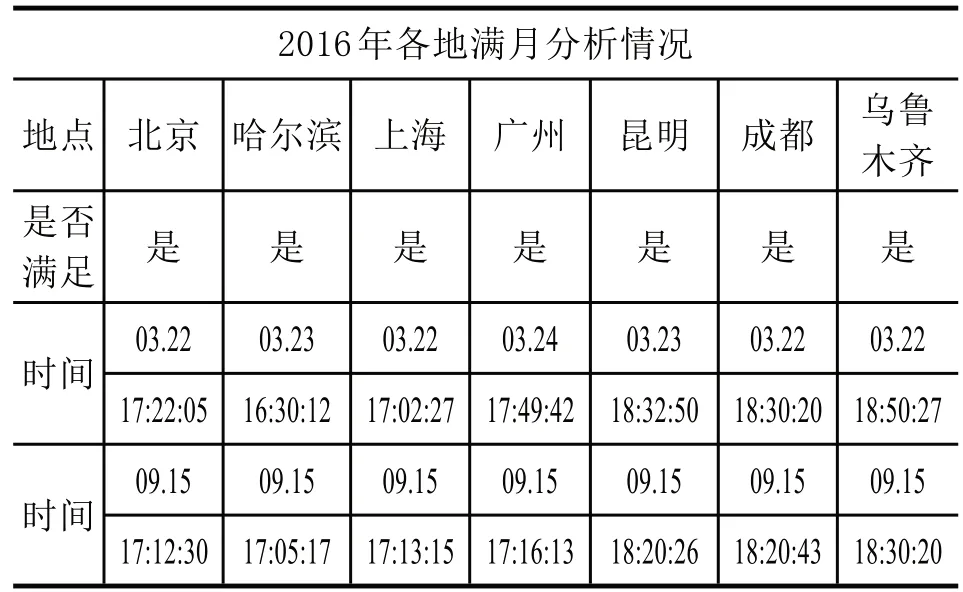
表4 2016 年各地满足“月上柳梢头,人约黄昏后”的时间表
5 模型评价
优点:本题解题过程和所构建的模型简单明了,且易用于实际生活中;对于题目有较为深刻的吻合,模型具有坚实可靠的数学基础;把天文知识和已经学习过的数学知识结合得比较好.
缺点:由于忽略因数较多,对运算结果与真实情况有稍微偏差,考虑的影响因素较少,在处理问题时可能存在一些误差.
