基于QM-DBSCAN的风力机数据清洗方法
2022-01-04郑玉巧刘玉涵何正文魏剑峰
郑玉巧, 刘玉涵, 何正文, 董 博, 魏剑峰
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
随着环境污染与能源危机等问题日益成为全球关注的焦点,风力发电作为最具开发与商业化前景的可再生能源发电形式越来越受到各国广泛关注[1-2].风电功率的周期性、随机性及间歇性等特征导致大规模风电并网对电力系统的影响越来越明显.利用数据挖掘与机器学习等算法研究风力发电的风速-功率规律,以解决风电并网对电力系统的影响已日益成为风电领域的一项重要课题.获得准确的风速-功率记录数据是前述课题的重要基础.
风电场所安装的数据采集与监测控制系统(supervisory control and data acquisition,SCADA)是风电场的风速-功率记录数据来源,该记录数据对风速-功率相关研究尤为重要.但在实际发电过程中,由于电力系统消纳能力的限制,使得风电场需要弃风,导致SCADA系统记录的风速-功率数据存在大量异常数据簇.这些数据簇具有集中、横向分布等特点,因此不能有效表征风力机实际运行过程中风速与功率间的关联关系.由此可见,如何清洗风速-功率数据中大量异常数据簇尤为关键.
诸多学者已对风速-功率数据清洗进行了大量研究.娄建楼等[3]提出最优组内方差清洗算法对风速-功率数据进行清洗,改变了传统方法对多维度数据的依赖性.赵永宁等[4]采用四分位法剔除风速-功率数据中的分散型数据,并使用k均值聚类剔除堆积型数据.朱倩雯等[5]在研究风速-功率数据时序重构时同样采用四分位法清洗了约22.67%的异常数据,四分位法清洗效果显著.邹同华等[6]研究表明采用Thompson tau-四分位法清洗风速-功率异常数据簇效果显著,有效解决了风电机组风速-功率异常数据处理方法清洗时间长、模型复杂的问题.张小奇等[7]在发电功率计算研究的过程中使用k均值聚类清洗数据,并取得了良好的效果.丁明等[8]在研究风力机发电量短期预测问题中使用自组织神经网络对功率数据进行清洗,进一步提升了风力机发电量短期预测精度.杨茂等[9]在风速-功率数据中考虑风向变化的同时还对上升风与下降风进行了有效区分,据此建立异常数据识别模型,该成果明确了异常数据簇的类型.张东英等[10]对风速-功率数据中的时序限风区间进行识别,全天整体识别率超过70%.Shen等[11]将风速-功率异常数据簇分为4类,并采用分组进行的四分位法剔除异常数据.Long 等[12]对风速-功率数据进行二值图像的转化,并建立数据点与图像像素间的映射关系,最后通过数学形态学方法(MMO)提取异常数据,这种方式效果显著.Ying 等[13]通过散点图拟合出风速-功率曲线,将曲线之外的数据识别为异常数据,该方式区分接近正常数据的异常数据簇的准确度有待进一步提高.
基于上述研究,针对在清洗风速-功率数据工作中正常数据与异常数据接近时以及产生密集堆积异常数据簇时出现清洗失效的情况,本文提出了一种用于识别清洗风速-功率数据的QM-DBSCAN聚类算法.该算法根据异常数据簇类别与特点进行区分,采用QM-DBSCAN聚类算法对风速-功率数据展开数据清洗工作.最后将该算法与广泛认同的四分位法、标准DBSCAN算法的识别清洗效果进行比较,验证所提方法的有效性.
1 数据清洗方法
1.1 四分位法
四分位数是指将一个排好序的数据样本平均划分成四部分的3个数据点,每部分所包含的数据量是整个数据样本数据量的25%.一个升序排列的样本集合X=[x1,x2,…,xn],四分位法(quartile method,QM)求解方法如下[14]:
1) 计算第二个四分位数Q2

(1)
2) 计算第一个和第三个四分位数Q1及Q3
当n=2k(k=1,2,…)时,从Q2将样本X分为两个子序列,分别求解两子序列的中位数Q′2、Q″2,则有Q1=Q′2,Q3=Q″2.
当n=4k+3(k=1,2,…)时,有
(2)
当n=4k+1(k=1,2,…)时,有
(3)
四分位距表示为
IQR=Q3-Q1
(4)
根据四分位距可确定样本X中异常值的内限为
R1,R2=Q1-1.5IQR,Q3+1.5IQR
(5)
超出内限[R1,R2]的值都为异常值.
1.2 基于密度的带噪声空间聚类算法
基于密度的带噪声空间聚类算法(density-based spatial clustering of applications with noise,DBSCAN)是一种典型的密度聚类算法.该算法可发现任意形状和数量的簇类,通过聚类将样本数据划分成不同的簇类,依此可判别出风电机组SCADA数据中的异常数据.DBSCAN算法中涉及两个重要参数,分别为邻域半径Eps和邻域内最少包含点数Minpts.给定一组风电机组SCADA数据点集合H={h1,h2,…,hn},相关定义如下:
Eps邻域:表示集合H中任意一点p的邻域半径Eps范围内点的集合.
核心点:若集合H中任意一点p的Eps邻域内至少包含了Minpts个数据点,则将点p标记为核心点.
边界点:不属于核心点,但属于在某个核心点的Eps邻域内的数据点.
噪声点:既不属于核心点,也不属于边界点的数据点,即异常点.
以Minpts=4为例,DBSCAN算法聚类过程示意图如图1所示.

图1 DBSCAN聚类示意图
图1中,黑色圆圈代表核心点,白色圆圈代表边界点,×代表噪声点.将数据点集合H中全部数据点对象标记为未访问状态,通过DBSCAN算法随机选取一个未访问的数据点p开始聚类;将p记为访问点,检查p的邻域半径Eps内是否至少包含Minpts个数据点对象,若包含,则将点p标记为核心点,核心点p创建一个新簇C,并将待选集合S中不属于其他簇的数据点对象添加至簇C中,直到集合H中的数据点全部访问完毕;最后将未添加的数据点划分为噪声点,即异常点.
2 风电场异常数据的分类
以国内某风电场F24号风电机组为研究对象,选取2018年7月1日零时至2019年7月1日零时的SCADA数据为基础数据,提取风速-功率数据总计54 607组,散点图如图2所示.
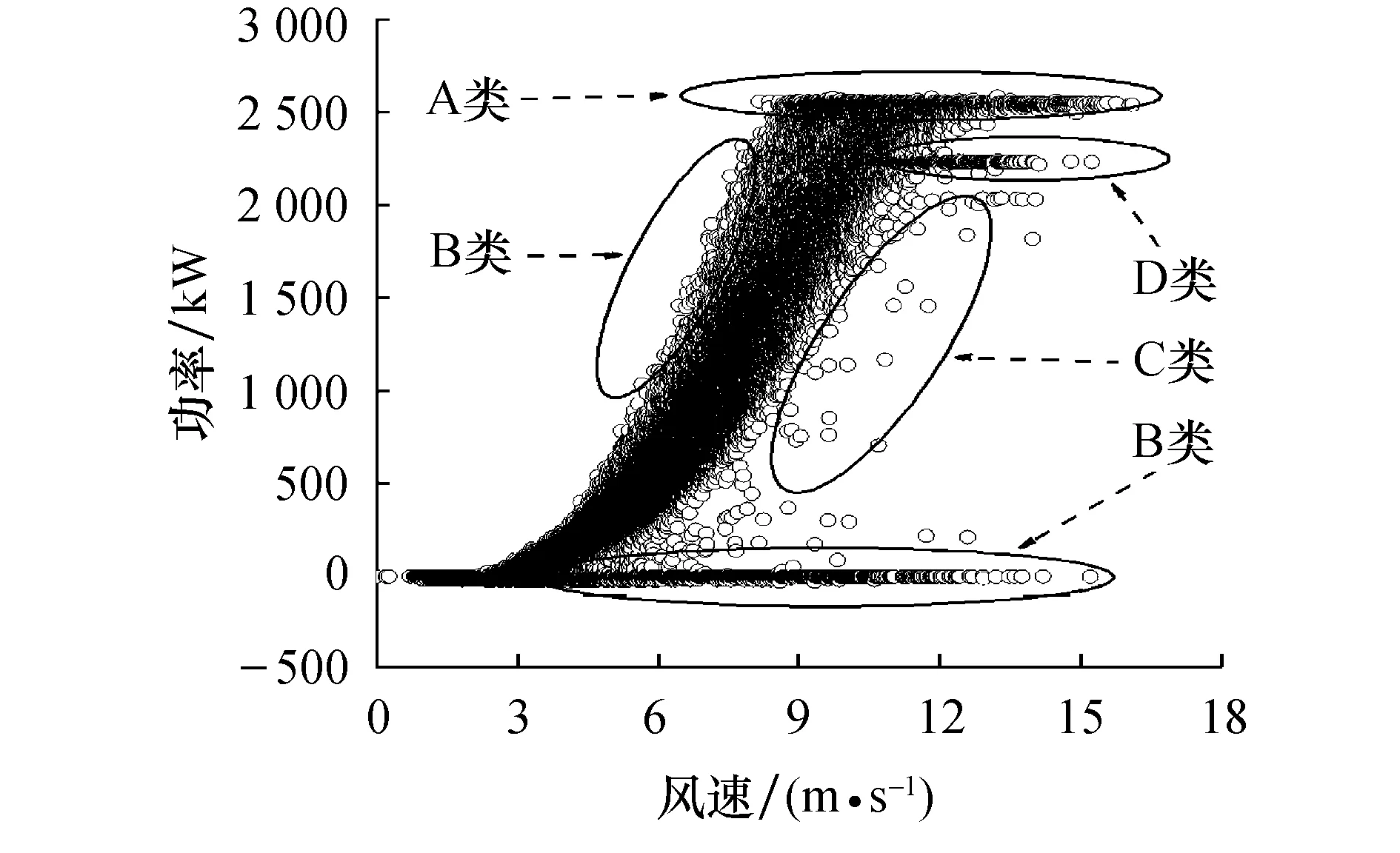
图2 风力机异常数据示意图
图2中根据异常数据的分布特点将异常数据大致分为4类,分别表示为A类数据、B类数据、C类数据及D类数据.其中,A类数据为超限数据,即记录功率值超过额定功率;B类数据为错误数据,即高风速下记录功率值为0或负值;C类数据为分散异常数据,即无规律、低密度分散在风功率曲线附近的记录功率值;D类数据为弃风限电数据,即1条及以上的横向密集散点,散点靠近风功率曲线附近时难以与正常数据分离.
3 案例分析
整理国内某风电场F24号风电机组由2018年7月1日零时至2019年7月1日零时的风速-功率数据记录.其中,A类数据共计1 775组,B类数据共计9 522组,总计11 297组数据.由于A类数据、B类数据的分布较集中且易于清洗,所以可直接剔除.
3.1 四分位法的应用
对于含有C类数据、D类数据的风速-功率数据序列,为得到显著清洗效果,可分别从横向和纵向两个维度依次进行清洗.
1) 横向清洗
剔除A类数据、B类数据后的风速-功率数据序列总计43 309组,按照风电机组输出功率从小到大的顺序对该数据重新进行排序,排序后的数据组记为N.然后以50 kW的间隔对数据组N等距划分区间,分别记为Ni(i=1,2,3,…,n;n=50).
在每个子数据组Ni内按照风速从小到大的顺序再次重新进行排序.根据式(1~3)分别计算每个新子数据组内的Q1位置、Q2位置及Q3位置,根据式(4)和式(5)确定R1位上限和R2位下限位置,以此确定正常数据范围,将范围外的数据视为异常值进行剔除.通过计算得到异常数据共计223组,异常值剔除后的风速-功率散点图如图3所示.

图3 横向清洗后风速-功率散点图
由图3可知,经过横向清洗后多数C类数据已被剔除,但仍存在部分C类数据和D类数据未被剔除,因此对横向清洗后的风速-功率数据再次进行纵向清洗.
2) 纵向清洗
横向清洗后的风速-功率数据序列总计43 086组,按照风电机组输出风速从小到大的顺序重新排序,排序后的数据组记为M,然后以0.5 m/s的间隔对数据组M等距划分区间.由于筛选后的风速最小值为0.71 m/s,最大值为14.1 m/s,故按照[0.5,14.5]的范围划分为28个子数据组,分别记为Mi(i=1,2,3,…,n;n=28).
在每个子数据组Mi内按照功率从小到大的顺序再次重新排序.根据式(1~3)分别计算每个新子数据组内的Q1位置、Q2位置及Q3位置,根据式(4)和式(5)确定R1位上限和R2位下限位置,以此确定正常数据的范围,将范围外的数据视为异常值进行剔除.统计得到异常数据共计584组,异常值剔除后的风速-功率散点图如图4所示.
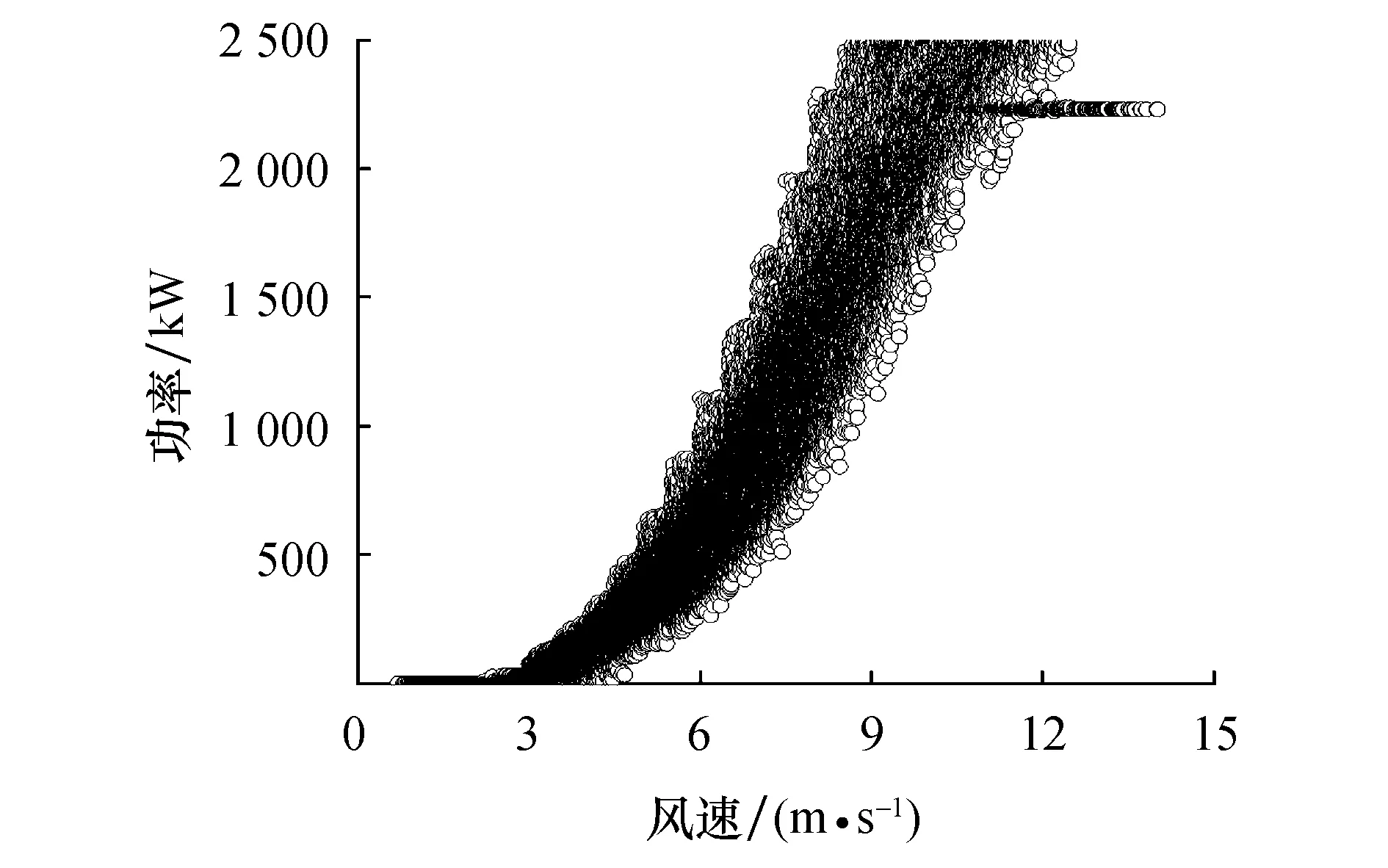
图4 纵向清洗后风速-功率散点图
由图4可知,纵向清洗后仍存在1条中部积聚型异常数据,观察到该异常数据大致呈现为1条输出功率为2 220 kW左右的横向数据带,为弃风限电数据.可见四分位法虽然可识别并剔除多数的C类数据和D类数据,但是部分区间内的C类数据和D类数据量过多会导致四分位法错误地把异常数据判定为正常值而继续保留,无法达到识别并剔除异常数据的目的.
3.2 DBSCAN算法的应用
3.2.1参数的设定
确定邻域半径Eps和邻域内最少包含点数Minpts是使用DBSCAN算法进行聚类的前提,Eps和Minpts的取值将直接影响到聚类效果.若Eps取值过大,则导致所有样本点都被划分到同一个簇;若Eps取值过小,则样本数据集合中可能没有核心点,且导致所有点可能都被标记为噪声.DBSCAN算法提出者Martin Ester将Minpts的取值设置为4,矩阵第k列称为k最近邻距离值,做出k距离图,通过观察法确定k距离图中曲线从平缓到陡峭的数据点,并以此作为Eps取值.但是主观观察存在一定的误差,导致Eps取值不够准确.因此用如下方法来确定Eps取值:
1) 由于k距离曲线的平缓性和陡峭性可以通过斜率值体现出来,所以求解k距离图中的每个点相对于下一点的斜率值,得到斜率数据组P;
2) 然后计算斜率数据组P中所有非零斜率的平均值和标准差;
3) 最后找出第一个大于平均值和标准差之后的斜率值,此斜率值所对应的k距离值即为Eps取值[15].
3.2.2使用DBSCAN算法
为达到良好的聚类效果,将风速-功率数据按照0.5 m/s的风速区间间隔进行划分,部分风速区间内的Eps和Minpts取值如表1所列.
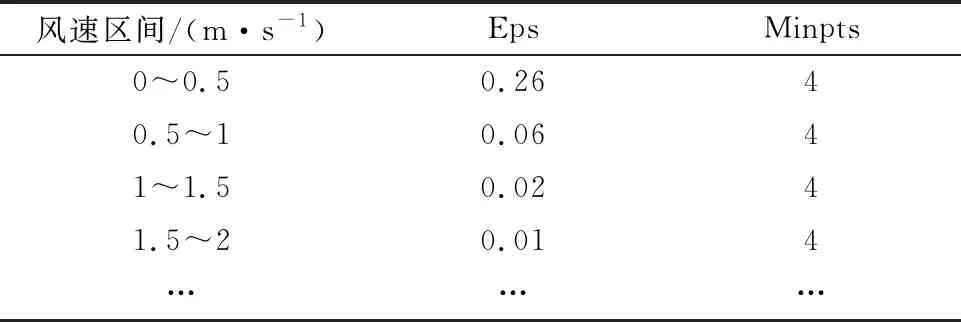
表1 QM方法处理后部分风速区间内的Eps和Minpts取值
聚类完成后绘制所有风速区间内的风速-功率散点图,如图5所示.

图5 DBSCAN聚类后风速-功率散点图
将图5中异常数据剔除后的风速-功率散点图如图6所示.

图6 DBSCAN处理后风速-功率散点图
由图6可知,图中仍存在部分C类数据和D类数据未被剔除,剔除效果并不理想.同时,DBSCAN算法的参数Eps受到聚类区间内所有数据点的影响,风速区间内异常数据过多或数据分布范围分散都会影响Eps参数取值,导致误将异常数据当做正常数据保留,进而出现图6所示的情况.
3.3 QM-DBSCAN算法的应用
从以上分析可知,四分位法和DBSCAN算法均可识别清洗异常数据,但实际应用中在异常数据过多或数据分布范围分散的情况下,单独使用四分位法或DBSCAN方法都无法达到理想的清洗效果.由于两种方法各有优势,四分位法可识别并剔除多数分布范围分散的数据,而DBSCAN法在数据分布范围集中时具有优良的聚类效果, 故可以考虑应用四分位法剔除分布范围分散的异常数据,然后再应用DBSCAN法进行聚类.基于此,提出一种基于QM-DBSCAN算法的数据清洗方法,具体步骤如下:
1) 对风速-功率数据应用四分位法进行横向清洗;
2) 横向清洗后的风速最小值为0.71 m/s,最大值为14.1 m/s;然后将横向清洗后的风速-功率数据按照0.5 m/s的风速区间间隔进行划分;
3) 由3.2节给出的参数确定方法确定每个风速区间内的Minpts和Eps取值,部分风速区间内的Eps和Minpts取值如表2所列.

表2 QM-DBSCAN处理后部分风速区间内的Eps和Minpts取值
4) 确定每个风速区间的Eps和Minpts取值后,对每个风速区间内进行聚类;然后对每个风速区间内的正常数据与异常数据进行标记并汇总,绘制风速-功率散点图,如图7所示.剔除异常数据后得到风速-功率散点图,如图8所示.

图7 QM-DBSCAN聚类后风速-功率散点图

图8 QM-DBSCAN处理后风速-功率散点图
由图4、图6和图8可知,四分位法和DBSCAN法清洗结果都未处理掉的异常数据在图8中已剔除,因此提出的QM-DBSCAN方法效果显著.为进一步从定量方面描述,选用spearman系数作为评价指标进行对比.
3.4 评价指标
相关系数可以从定量角度描述两个变量间的相关程度.由于风电机组的风速与功率有很强的相关性,故可用相关系数作为评价指标判定风速-功率数据清洗前后的相关性强弱,相关性越强代表清洗效果越好.由于spearman相关系数具有很强的通用性,故选作评价指标对3种数据清洗方法(四分位法、DBSCAN法、QM-DBSCAN法)进行对比评价.给定一组风速-功率数据S={(x1,y1), (x2,y2),…,(xn,yn)},其中,i=1,2,…,n.则spearman相关系数求解公式为

(6)
分别求解3种不同方法对风速-功率数据处理后的spearman系数,如表3所列.
由表3可知,QM-DBSCAN方法清洗后的风速-功率数据的spearman系数较四分位法、DBSCAN法分别提高了0.003 5和0.004 7,进一步说明所提出的QM-DBSCAN法优于其他2种方法.

表3 3种方法的spearman系数
4 结论
1) 选用风速-功率数据为清洗对象,根据异常数据的分布特征将其分为4类,分别表示为A类数据、B类数据、C类数据和D类数据.
2) 识别并剔除风速-功率异常数据时所应用的QM-DBSCAN法优于四分位法和DBSCAN法,spearman系数较四分位法和DBSCAN法分别提高了0.003 5和0.004 7,QM-DBSCAN法的剔除效果最好.
3) 本文所提出的方法可适用于其他研究对象的异常数据清洗工作,具有一定的推广意义.
