汽车动力总成全套悬置系统台架耐久模拟试验研究
2022-01-04徐有忠章礼文
徐有忠,章礼文
(1.奇瑞汽车股份有限公司 汽车工程研究总院,安徽 芜湖 241009; 2.安徽省汽车NVH与可靠性重点实验室,安徽 芜湖 241009)
0 引 言
悬置系统是连接动力总成与车身的重要桥梁,它不仅起到约束动力总成位移、隔离并衰减振动与噪声等作用,还能吸收路面带来的激励和瞬态冲击,改变动力总成响应,从而提升汽车的舒适性[1]。其耐久可靠性关系到车辆噪声(noise)、振动(vibration)、声振粗糙度(harshness)即NVH性能的持续保持能力,直接影响用户使用,因此至关重要。
汽车耐久性试验包含实车道路试验和室内台架模拟试验。与道路试验相比,台架试验周期短、重复性好[2],对应的载荷谱处理方法及应用研究越来越多。文献[3]重点围绕载荷处理,综述了基于时域和频域信号迭代来提升台架模拟精度的方法;文献[4]对不同耐久试验方法、技术及流程进行了研究;文献[5]提出了一种基于各路段最小标准差谱组合的试验场实测载荷谱选取新方法;文献[6]提出基于小波变换和损伤保留2种方法来编辑载荷谱。
在实际车型开发中,悬置阻尼与刚度特性通常都需要多轮次的调校优化,更需要采用高效的台架模拟试验来快速验证与确认。针对悬置系统的耐久性及其室内台架模拟试验方法,国内外学者开展了大量的研究。文献[7]基于远程控制参数技术远程程序控制(remote program control,RPC)重构发动机悬置道路载荷谱,建立总载荷序列来验证单个液压悬置的耐久性[7];文献[8]对悬置总成、金属支架和壳体分别开展动态疲劳强度试验,基于损伤等效的多轴载荷和温度条件(通过引入温度箱进行模拟)来考核悬置总成的疲劳耐久强度;文献[9]基于多轴模拟试验台(multi-axial simulation table,MAST),通过6个作动器模拟车辆6个方向的运动,精确再现动力总成全套(3个)悬置系统在路试中的运行环境;文献[10]基于六自由度振动台的道路试验模拟方法,复现客车动力总成全套(4个)悬置系统在实车路试中的运行工况;文献[11]研究了24通道整车道路台架上与道路试验中动力总成各个悬置系统主被动两端加速载荷谱的差异[11]。
为了更好地模拟动力总成悬置实际复杂的承载条件与运行环境,本文提出一种可以同时对全套悬置系统进行完整激励加载的台架耐久模拟试验方法。针对不同路况特点采用不同的相应控制迭代方案形成驱动载荷谱,与文献[9-10]仅用6个作动器对MAST进行6个方向加载不同,本文还在动力总成两端连接的左右驱动轴上施加扭矩谱,同时还模拟发动机运行时舱内温度变化来动态设定温度。对比试验结果表明,本文方法有效提升了悬置系统台架模拟的精度。
1 悬置系统试验设计
1.1 试验台架设计
为了尽量模拟实车状态,将动力总成和全套悬置系统完全按前舱布置参数,安装在MTS公司六自由度MAST振动台上。台架设计原理如图1所示。
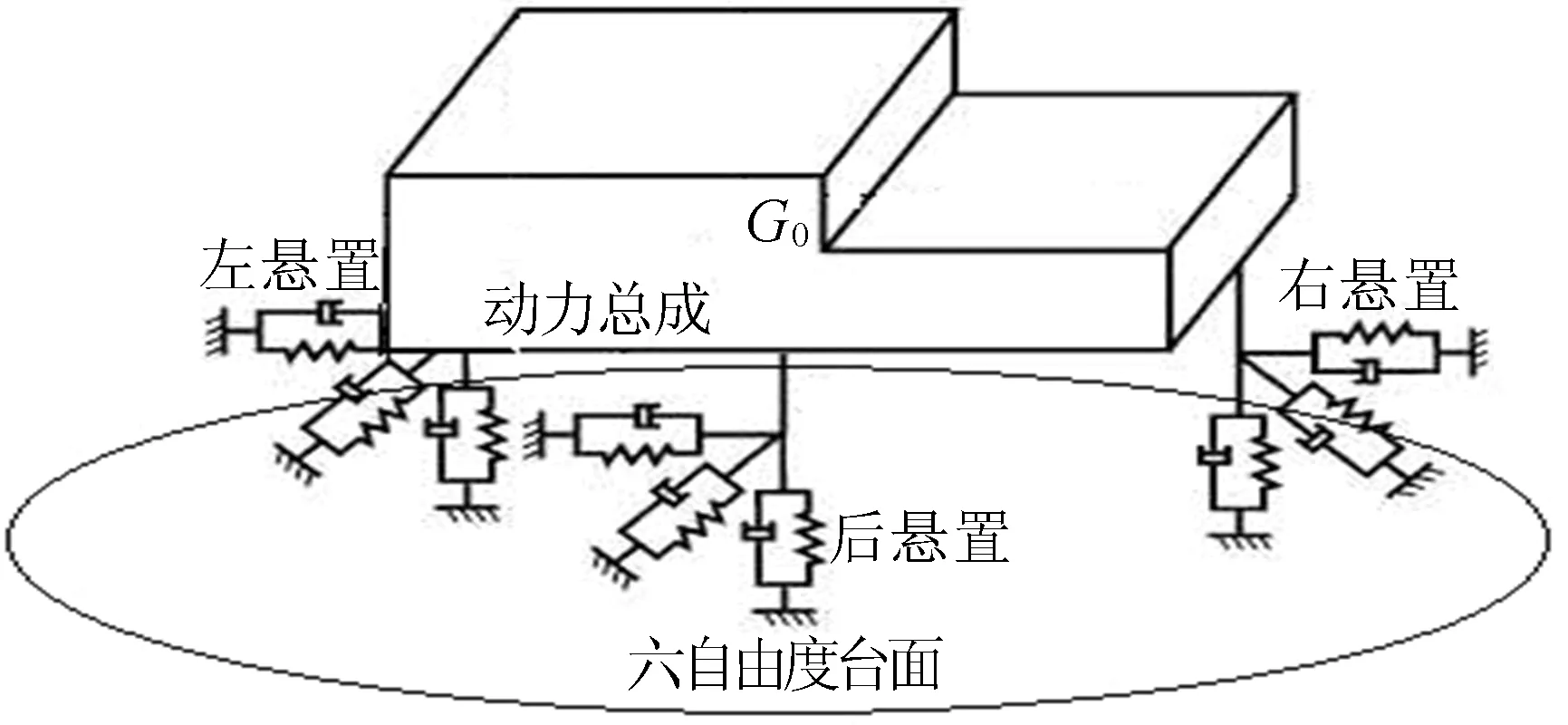
图1 动力总成悬置系统试验原理
台架具体设计图如图2所示。
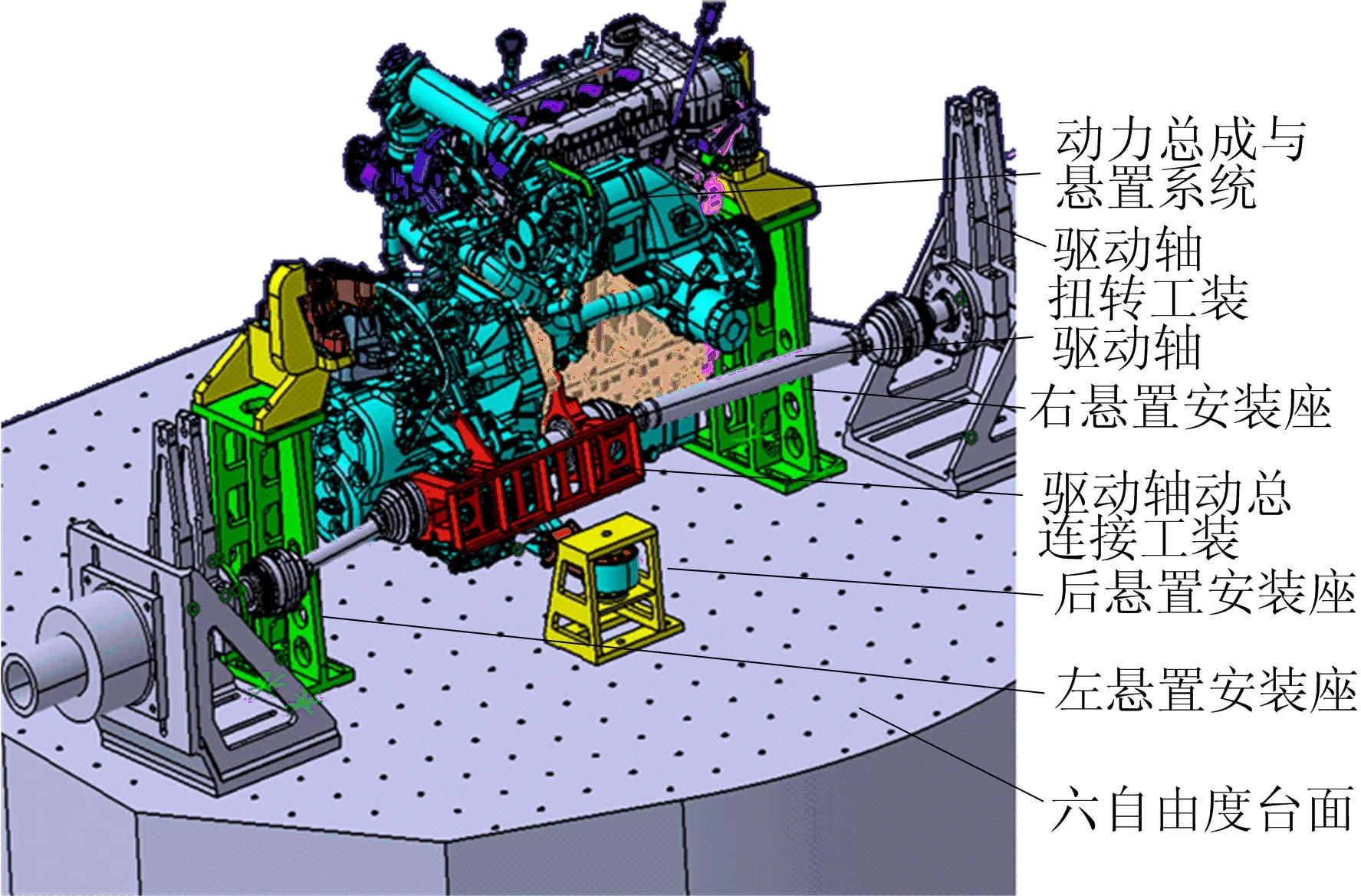
图2 动力总成悬置系统试验安装示意图
图2中,整个动力总成通过左、右悬置和后悬置系统及其安装座固定在六自由度振动台台面上,变速箱两端通过左、右驱动轴与驱动轴扭转工装连接,驱动轴与动力总成通过工装刚性连接。试验工装与夹具的设计要求较高,否则会影响道路模拟试验的效果,其设计应满足的原则[7]如下:
(1) 工装夹具的半功率带宽范围避开测试频率,其固有频率应大于400 Hz以上。
(2) 工装夹具的各向刚度足够大,确保受力后其变形对试验结果影响足够小。
(3) 工装夹具约束面与实际零件安装接触面积相同。
在带环境舱的MAST台架模拟试验中,通过温控系统来实现环境舱内悬置系统的温度与实际温度保持一致相对容易,相对复杂的是在六自由度振动台上再现道路试验中的运动载荷条件,包括迭代模拟悬置系统运动状态和驱动轴扭转载荷状态。
1.2 载荷试验迭代流程
悬置系统载荷迭代流程如图3所示。
图3中,利用数据采集设备采集载荷谱,包括道路试验车各悬置的三向加速度(悬置系统主被动两端——动总侧、车身侧)、质心三向加速度和驱动轴扭矩载荷谱。
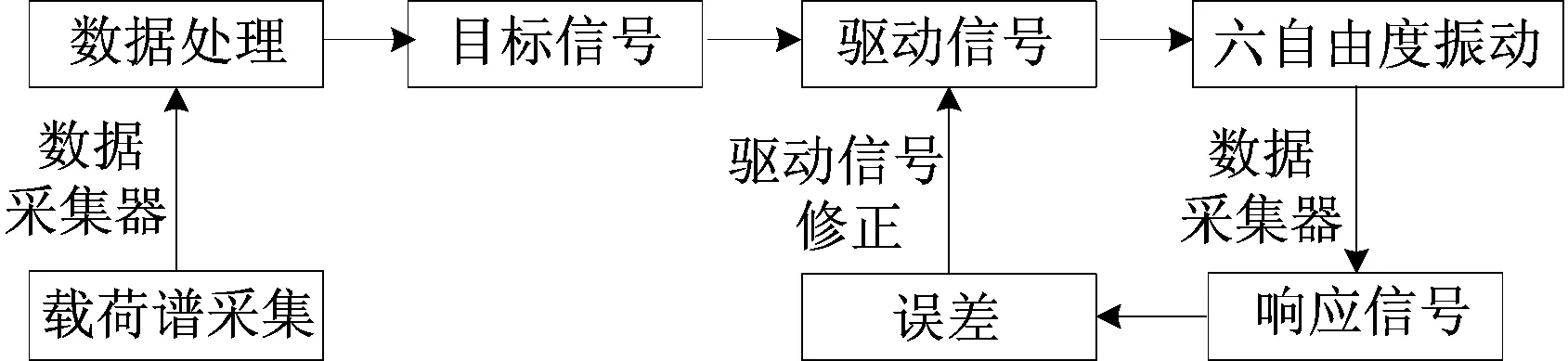
图3 悬置系统载荷迭代流程
1.3 载荷试验迭代方案
本文通过分析比较,制定悬置系统主要载荷的5种迭代方案,具体如下:
(1) 方案1为“驱动轴扭矩+车身侧加速度”信号控制迭代。
(2) 方案2为“驱动轴扭矩+(车身侧+质心)加速度”信号控制迭代。
(3) 方案3为“驱动轴扭矩+(车身侧+质心+动总侧)加速度”信号控制迭代。
(4) 方案4为“驱动轴扭矩+动总侧加速度”信号控制迭代。
(5) 方案5为“驱动轴扭矩+质心加速度”信号控制迭代。
将迭代得到的台架载荷谱与道路试验中采集的载荷谱进行精度比较,可以确定最佳迭代方案。
2 试验相关的关键处理
2.1 悬置系统道路载荷谱采集
整车道路试验中所采用的道路覆盖了车辆用户在使用过程中可能遇到的30多种典型工况路面,如凹坑路、水泥波纹路、搓板路、鹅卵石路、比利时路、扭曲路和沙石路等。
本文对搭载整车综合耐久道路试验车辆的悬置系统道路载荷谱进行采集,使用HBM-SoMat公司生产的eDAQ数据采集系统,得到的采集通道(按2 048 Hz采样率进行载荷谱采集)及其与1.3节信号控制迭代方案对应的关系见表1所列。
表1中:加速度单位为g;扭矩单位为N·m;Ctrl表示控制信号;Mon表示监控信号;通道包括在动力总成悬置安装点的动总侧和车身侧各布置3个三向加速度传感器,在动总质心布置1个三向加速度传感器,在两侧驱动轴轴杆上安装扭矩测试应变片。三向加速度传感器和应变片安装图如图4所示。
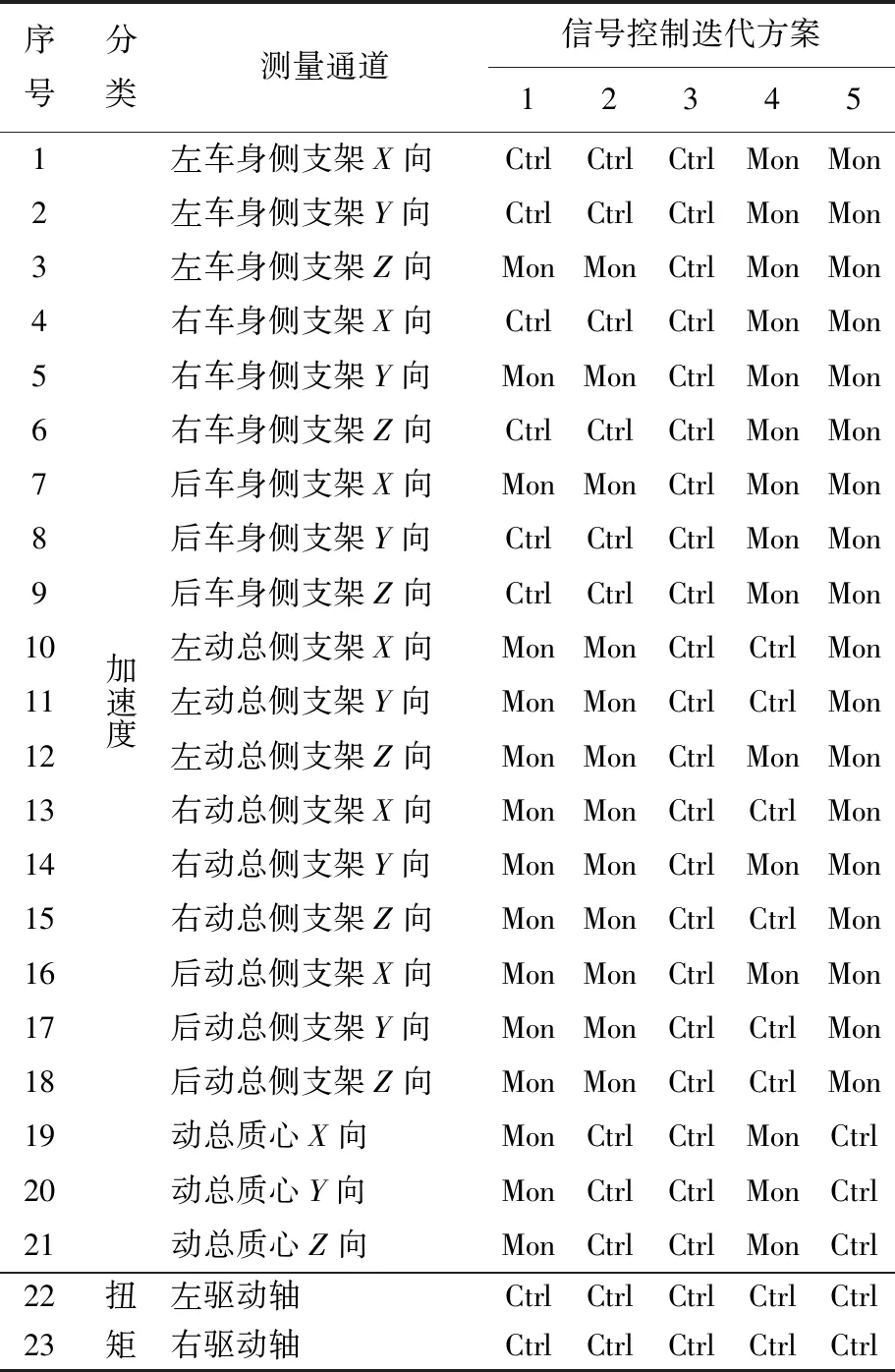
表1 道路载荷谱采集通道及信号控制迭代方案

图4 三向加速度和应变片安装图
2.2 台架通道设置
六自由度振动台驱动通道设置为3个平动方向Long、Lat、Vert,3个转动方向Roll、Pitch、Yaw,2个扭转方向TIF1、TIF2,见表2所列。
2.3 载荷谱编辑
对试车场采集到的原始路谱进行重采样、去均值以及剪切等编辑处理,同时去除毛刺等异常数据,平滑过渡断点,保持通道间相位关系[5,10]。编辑数据的主要目的是把原采集的数据进行修正和压缩,缩短试验周期。按照损伤等效原则,删去信号中无损伤或小损伤信号[6],使编辑后的数据保留原始路谱98%以上的损伤值,得到台架试验的目标响应谱。悬置系统载荷谱压缩编辑流程界面如图5所示。
2.4 输入输出信号之间关系建立
假设系统为线性系统,可以根据系统的输入输出信号与频响函数的关系由试验的目标信号和频响逆函数矩阵反推得到所需的驱动信号。由于实际系统的各个环节(如驱动系统、悬置系统、测量系统等)都存在一定程度上的非线性,根据线性系统计算出的驱动信号去激励系统时得到的响应与期望响应存在很大的误差。为了消除非线性的影响,需要使用迭代的方法逐步修正驱动信号,使系统的响应逼近目标信号。试验迭代的输入、输出关系如图6所示。
由图6可知,试验系统包括伺服控制器、驱动系统(作动器)、悬置系统和信号测量系统,输入信号向量为X,输出信号向量为Y。迭代之前,六自由度振动台设置生成一个白噪声驱动谱(表2中的8个通道),其频率和幅值覆盖道路载荷谱。根据白噪声驱动系统获得响应通道的响应谱(输出信号Y)和输入信号X,可以求得频响函数矩阵H[2,3,9,10],即
H=YT/XT
(1)
其中:输出信号Y=[y1y2y3…ym],m为输出信号数,由表2可知m=8;输入信号X=[x1x2x3…xn],n为输入信号数,实际由方案1~方案5确定;频响函数H为m×n矩阵。
由(1)式可知,输出信号Y可以表示为:
YT=HXT
(2)
即
(3)
由(3)式可得:
i=1,2,3,…,m
(4)
3 载荷谱迭代
3.1 迭代计算步骤
根据上述输入信号与输出信号之间的关系,得到如下的载荷谱迭代计算具体步骤。
(1) 利用系统频响函数H-1与已编辑好的目标信号Ydesire,计算得到初始驱动信号X0。
(2) 加载初始驱动信号X0,生成初始响应信号Y0。
(3) 比较初始响应信号Y0与目标信号Ydesire,将两者的差值乘以系统频响函数的逆矩阵H-1,再乘迭代因子g,加上初始驱动信号X0,计算得到第1次驱动信号X1。
(4) 重复步骤(2)和步骤(3),依次得到第1次响应信号Y1和第2次驱动信号X2、第2次响应信号Y2和第3次驱动信号X3、第3次响应信号Y3和第4次驱动信号X4,直至迭代到第n次响应信号Yn与目标信号Ydesire差值的均方根值与目标信号Ydesire的均方根值之比小于规定值(一般为≤15%)时,停止迭代。
(5) 以停止迭代时的驱动信号Xn作为最终的系统驱动信号[9-10]。
3.2 最佳迭代方案获取
按上述试验迭代计算步骤,对1.3节给出的5种方案分别开展迭代计算。
对道路载荷谱进行编辑处理,删除对悬置系统损伤贡献小的小幅值信号,得到目标载荷信号[7]。计算MAST驱动谱和路试中悬置系统加速度之间、台架扭矩和路试扭矩之间的传递函数,通过迭代求取MAST的驱动谱,保证全套悬置系统响应信号与目标信号接近一致[9-10]。
将迭代得到的台架载荷谱与道路试验中采集的载荷谱进行精度比较,获得台架试验结果与目标信号较吻合的最佳方案。
限于篇幅,本文仅给出通过大量的试验方案迭代及比较得出的最佳试验迭代方案,即驱动轴扭矩与车身侧加速度信号控制迭代方案1,而在出现共振路况部分,采用驱动轴扭矩与动总质心加速度控制迭代方案5。
比利时路面是一种典型的凸凹坏路,为整齐石块路面[12],这种路面在整车道路耐久试验时很容易出现共振,因此最佳试验方案必须采用控制迭代方案5。其他30多种典型路面工况,没有出现共振,因此最佳试验方案应采用控制迭代方案1。
比利时路面容易产生共振,相较于其他路面工况控制迭代收敛更难。由于篇幅所限,下文以比利时路面工况为例来展示迭代结果:① 发动机悬置车身侧和动总质心三向加速度(X、Y、Z3个方向)的响应信号与目标信号的时域比较;② 响应信号与目标信号的频域比较;③ 均方根误差统计值、均方根响应统计值、相对伪损伤。
4 目标信号的道路模拟
4.1 时域信号比较
对比利时路面工况采用迭代方案5迭代后,发动机悬置车身侧和动总质心三向加速度响应信号与目标信号的时域比较如图7所示。图7中,蓝色和红色分别代表目标和响应信号,下文同。
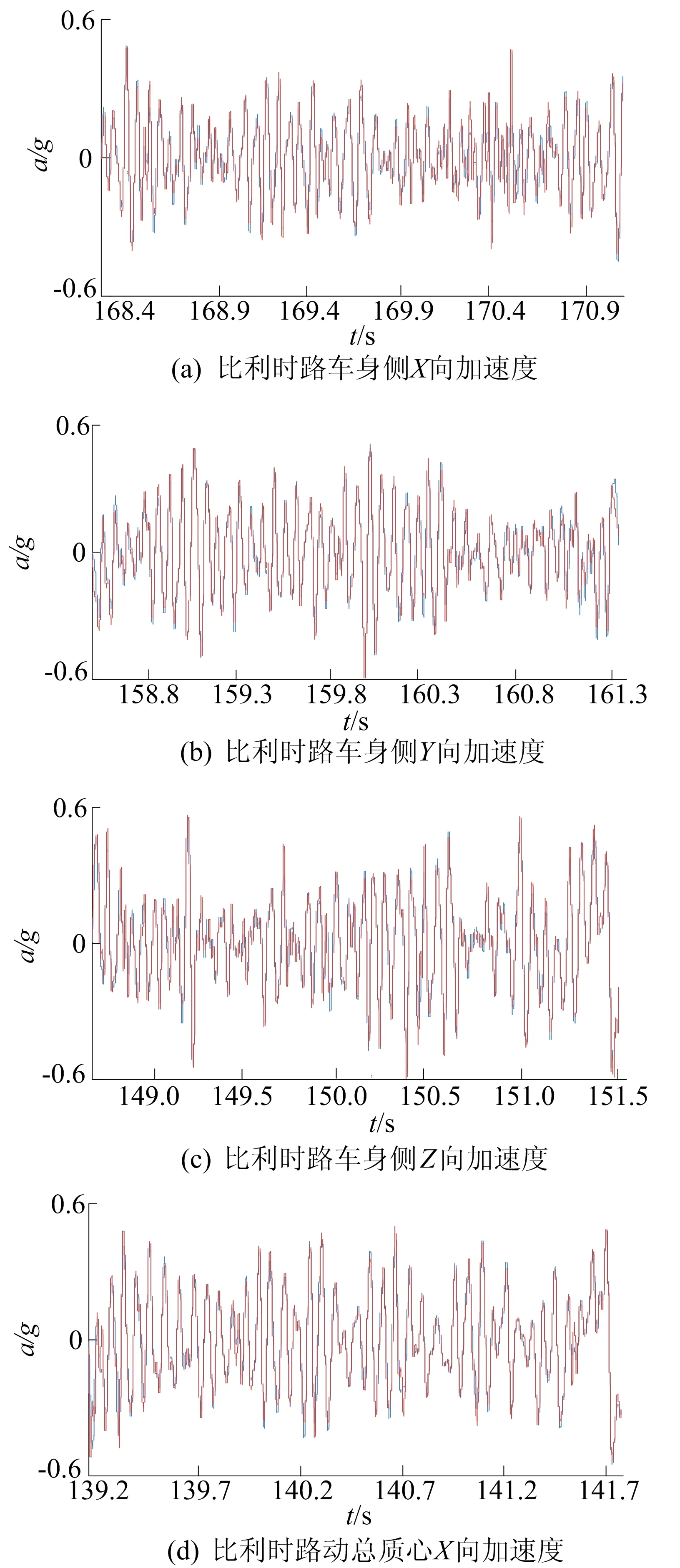
图7 时域加速度响应信号与目标信号的比较
4.2 频域信号比较
对比利时路面工况采用迭代方案5迭代后,发动机悬置车身侧和动总质心三向加速度响应信号与目标信号的频域比较如图8所示。其中,PSD为功率谱密度。
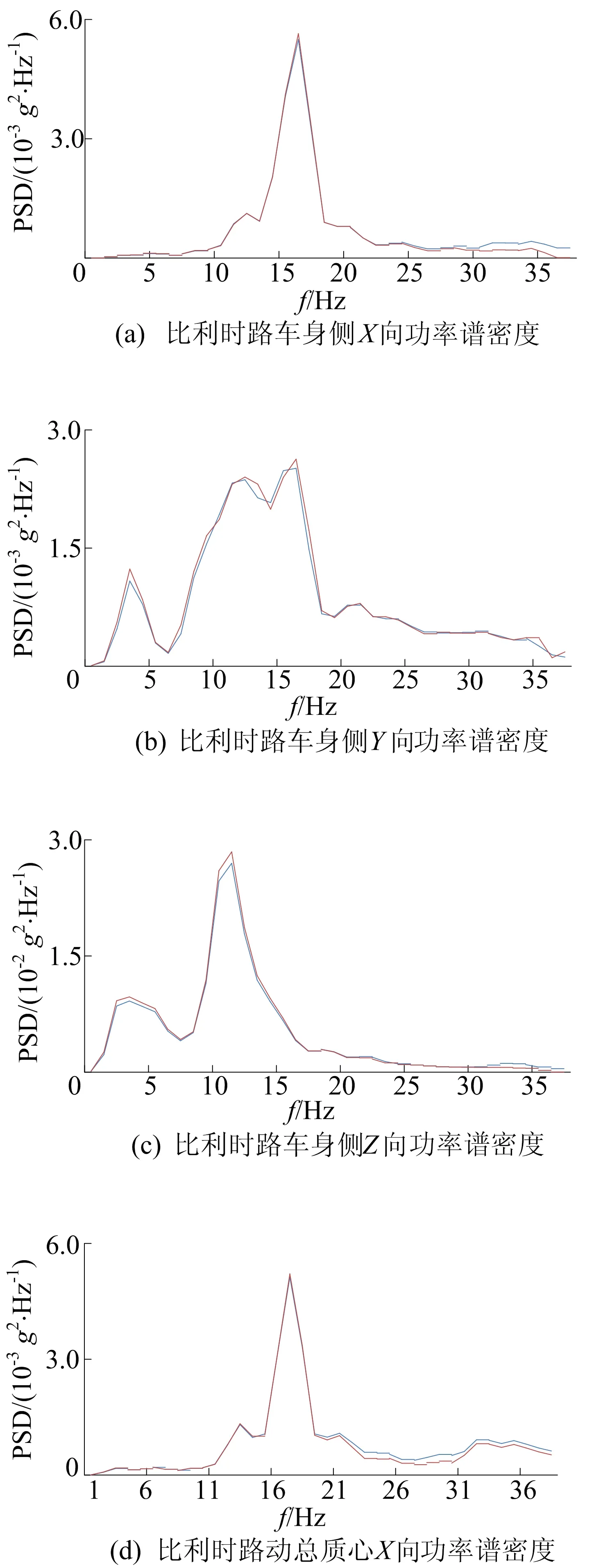
图8 频域加速度响应信号与目标信号比较
从图7和图8可以看出,台架响应信号与目标信号在时域和频域中几乎重合,这充分说明悬置系统在台架上的受力状态与在试车场中行驶的受力状态几乎相同,表明迭代结果的精度很高。
4.3 迭代误差分析
均方根误差统计值效果如图9所示。图9中,纵坐标为台架信号误差均方根与路试信号均方根比值的百分数。

图9 比利时路均方根误差统计值收敛情况
均方根响应统计值如图10所示。图10中,纵坐标为台架信号均方根与路试信号均方根比值的百分数。
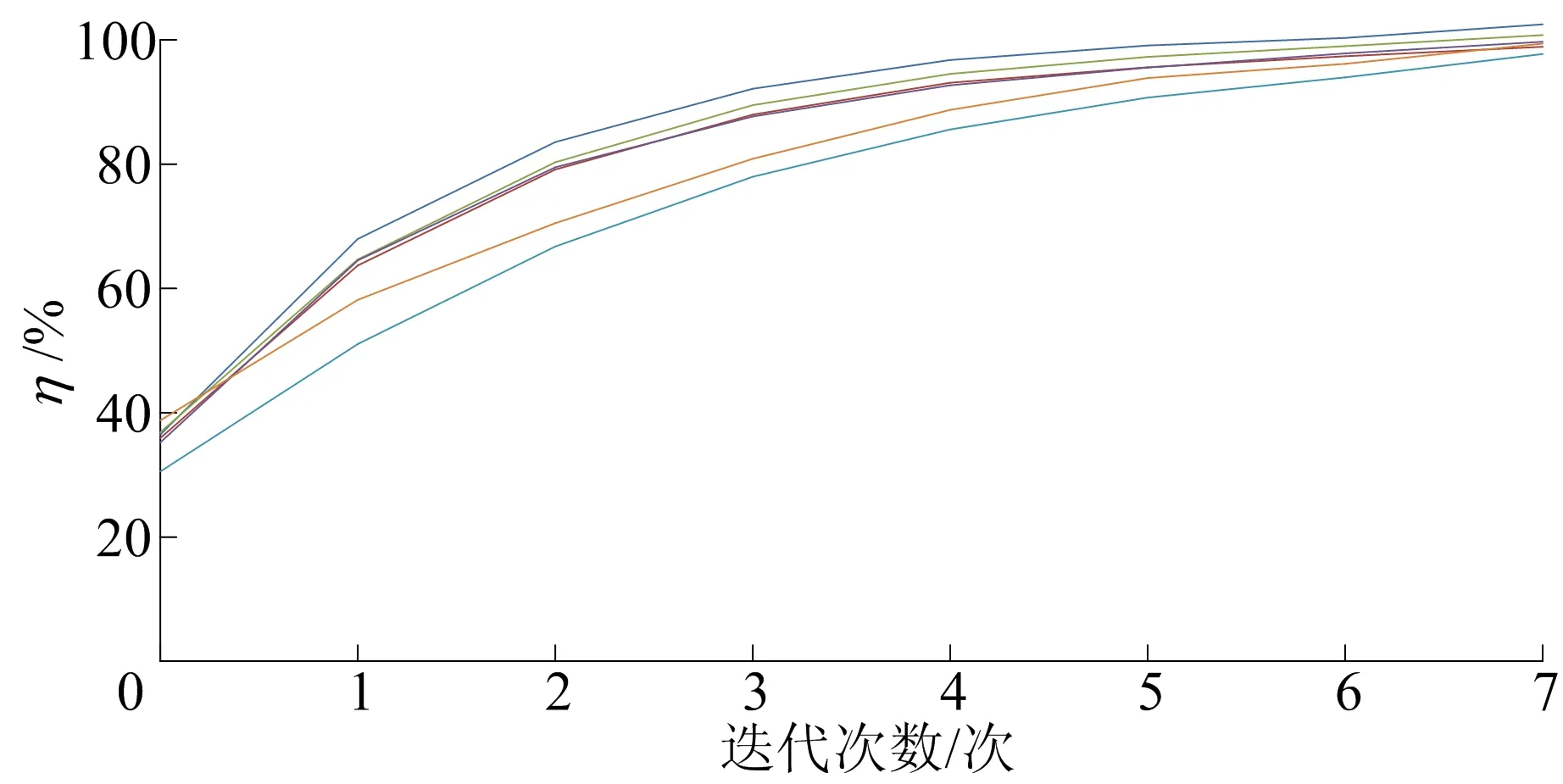
图10 比利时路均方根响应统计值情况
由图9可知,试验迭代的均方根误差统计值小于等于15%;由图10可知,均方根响应统计值大于等于95%。图9和10表明,迭代获得的计算结果均较为合理,满足误差要求。
迭代后,台架驱动响应信号的相对伪损伤如图11所示。其中:通道1表示左车身侧支架X向加速度;通道2表示左车身侧支架Y向加速度;通道3表示左车身侧支架Z向加速度;通道4表示右车身侧支架X向加速度;通道5表示右车身侧支架Y向加速度;通道6表示右车身侧支架Z向加速度;通道7表示后车身侧支架X向加速度;通道8表示后车身侧支架Y向加速度;通道9表示后车身侧支架Z向加速度;通道10表示动总质心X向加速度;通道11表示动总质心Y向加速度;通道12表示动总质心Z向加速度;通道13表示左驱动轴扭矩;通道14表示右驱动轴扭矩。
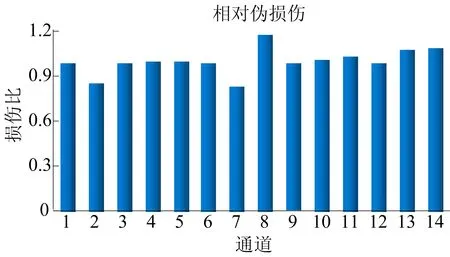
图11 相对伪损伤
由图11可知,相较于目标信号,迭代后台架驱动响应信号的相对伪损伤基本控制在0.8~1.2之间,各通道的相对损伤值均在可接受的范围内。
因此,迭代获得的驱动信号对路面实测的载荷复现得很好。
5 试验结果
整个台架模拟试验中应用了综合路试中采集的30多种典型路面工况对应的载荷谱来验证全套悬置系统的耐久性能。
为了验证动力总成全套悬置系统台架耐久模拟试验方法的有效性,在某车型开发中,开展第1轮综合道路试验验证的同时,基于带环境温度舱的MAST,搭建如图2所示的包含动力总成、3个悬置系统、左右驱动轴在内的系统台架试验,通过加载驱动谱和设定温度条件开展环境舱内的全套悬置系统的台架模拟试验。
模拟实际环境控制悬置系统的温度,按照最佳试验迭代方案,将前述迭代停止时的驱动信号Xn作为最终的驱动信号Xdrive,按照道路试验规范循环顺序及次数将驱动信号串联成试验驱动谱,对悬置系统进行加载,以此来考核悬置系统的耐久可靠性。
在开展六自由度台架试验与综合道路试验后,均发现发动机左侧橡胶悬置系统出现失效,具体开裂的位置与裂纹情况如图12所示。
图12a所示为台架试验运行过程中,载荷谱对应整车路试当量里程约11 280 km时发动机左悬置总成出现开裂现象,裂纹长约5 mm,右悬置总成和后悬置总成均未失效。
图12b所示为在整车综合道路试验中,发动机左悬置总成在路试12 000 km时出现了开裂现象,开裂位置与台架上开裂位置一致,裂纹长约10 mm,右悬置总成和后悬置总成均未失效。
由图12可知,对于该车型发动机悬置系统的失效情况,这一轮台架试验结果与路试结果基本一致,验证了本文提出的动力总成全套悬置系统台架耐久模拟试验方法的有效性。

图12 悬置系统失效图
6 结 论
(1) 本文对六自由度振动台应用RPC技术,通过提出的试验迭代,有效地获得了悬置系统相关的驱动载荷谱。
(2) 比利时路面工况的案例表明,无论是车身侧加速信号,还是动总质心的加速信号,在时域和频域的迭代信号都能与采集信号吻合,且迭代精度满足误差要求。因此,本文提出的台架模拟迭代方法能有效再现路试悬置系统相关载荷谱。
(3) 台架模拟试验中, 左悬置出现故障的里程数与路试发现故障的里程比较接近, 且左悬置失效模式、开裂位置与形状也与路试情况高度吻合。因此,验证了本文提出的全套悬置系统台架耐久模拟试验方法是有效且可靠的。
(4) 本文提出的悬置系统台架耐久模拟试验方法不仅可以有效地对带有动力总成的全套悬置系统进行快速耐久验证,替代过去采用整车综合路试对悬置系统进行完整考核的验证手段,还可用于早期快速验证悬置系统设计方案,减少整车道路试验的轮次,从而提升整车产品的开发效率。
