基于快速和谐搜索算法的地下水污染源识别
2022-01-04骆乾坤李迎春钱家忠
叶 港,骆乾坤,李迎春,钱家忠
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽省公益性地质调查管理中心,安徽 合肥 230601)
0 引 言
地下水污染严重、水质型缺水问题已成为制约经济社会可持续发展的重要因素,因此亟需开展地下水污染修复与治理工作。准确掌握污染源相关信息,精确刻画污染物运移途径,是实现高效修复含水层污染的重要前提。一般来说,在污染源信息未知的情况下,需要根据观测井处的污染物质量浓度观测值反求出污染源的质量浓度、位置和泄露时间等信息,即地下水污染源识别问题[1-4]。
传统的数学方法或梯度方法进行污染源信息识别易陷入局部最优,难以求得全局最优解。相较之下,遗传算法[5]、人工神经网络[6]、禁忌搜索算法[7]、模拟退火算法[8]、粒子群算法[9]等启发式算法因强大的全局搜索能力而在地下水污染源识别领域得到广泛应用。文献[10]利用模拟含水层中污染物浓度资料,结合无网格模拟机,以径向点配置法与粒子群算法为优化器,建立模拟优化模型,以识别未知的地下水污染源;文献[11]采用自适应模拟退火法对地下水污染源进行三维识别;与经典的启发式搜索算法相比,文献[12]提出一种新的启发式算法,和谐搜索(harmony search, HS)算法;文献[13-14]对HS算法进行改进,提出改进和谐搜索(improved harmony search, IHS)算法,IHS算法提高了HS算法的精度和收敛速度;文献[15]对HS算法音节调整步骤进行进一步改进,提出快速和谐搜索(fast harmony search, FHS)算法,并已将其成功应用于求解水文地质参数识别问题,且证明了FHS算法比遗传算法、粒子群算法和改进和谐搜索算法具有更强的全局搜索能力、更快的收敛速度及求解精度。
基于FHS算法求解效率高、搜索能力强及收敛速度快的优点,本文拟将其引入到地下水污染源识别领域。本文通过将FHS算法与地下水流模拟软件MODFLOW、溶质运移模拟软件MT3DMS进行耦合,建立地下水污染源识别模拟-优化耦合模型,进而将其应用于污染源的质量浓度、位置和泄露时间与信息的识别,以期为地下水污染源识别问题提供高效可靠的求解方法。
1 地下水污染源识别模拟优化模型
1.1 地下水流及溶质运移模拟模型
1.1.1 水流模型
在不考虑水密度变化的条件下,孔隙介质中地下水在三维空间的流动可以用偏微分方程表示,即
(1)
其中:Ki,j(i,j=1,2,3)分别为渗透系数张量,下标1、2、3分别为x、y、z方向上的分量;h为水头;W为单位体积含水层中的体积流量,用以代表流进汇或流出源的水量;ss为孔隙介质的弹性释(贮)水率;t为时间。
本文采用MODFLOW模拟软件对地下水流模拟模型进行数值求解。
1.1.2 溶质运移模型
考虑地下水的对流、弥散、流体源/汇项、平衡吸附作用以及一级不可逆反应,化学组分k的三维运移偏微分方程为:
(2)
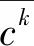
本文采用MT3DMS模拟软件对地下水溶质运移模拟模型进行数值求解。
1.2 地下水污染源识别优化模型
为了对污染源进行准确刻画,需要确定污染源质量浓度、位置和泄露时间的相关信息。本文目标函数需要表示出最准确的污染源信息描述,因此采用观测井处质量浓度模拟值与观测值的最小化误差平方和的均方根(root mean square error,RMSE)作为目标函数,建立以下优化模型。
目标函数为:
minE(ρ1,ρ2,…,ρn;Xp1,Xp2,…,Xpn;t1,t2)=
(3)
约束条件为:
ρmin<ρk<ρmax,
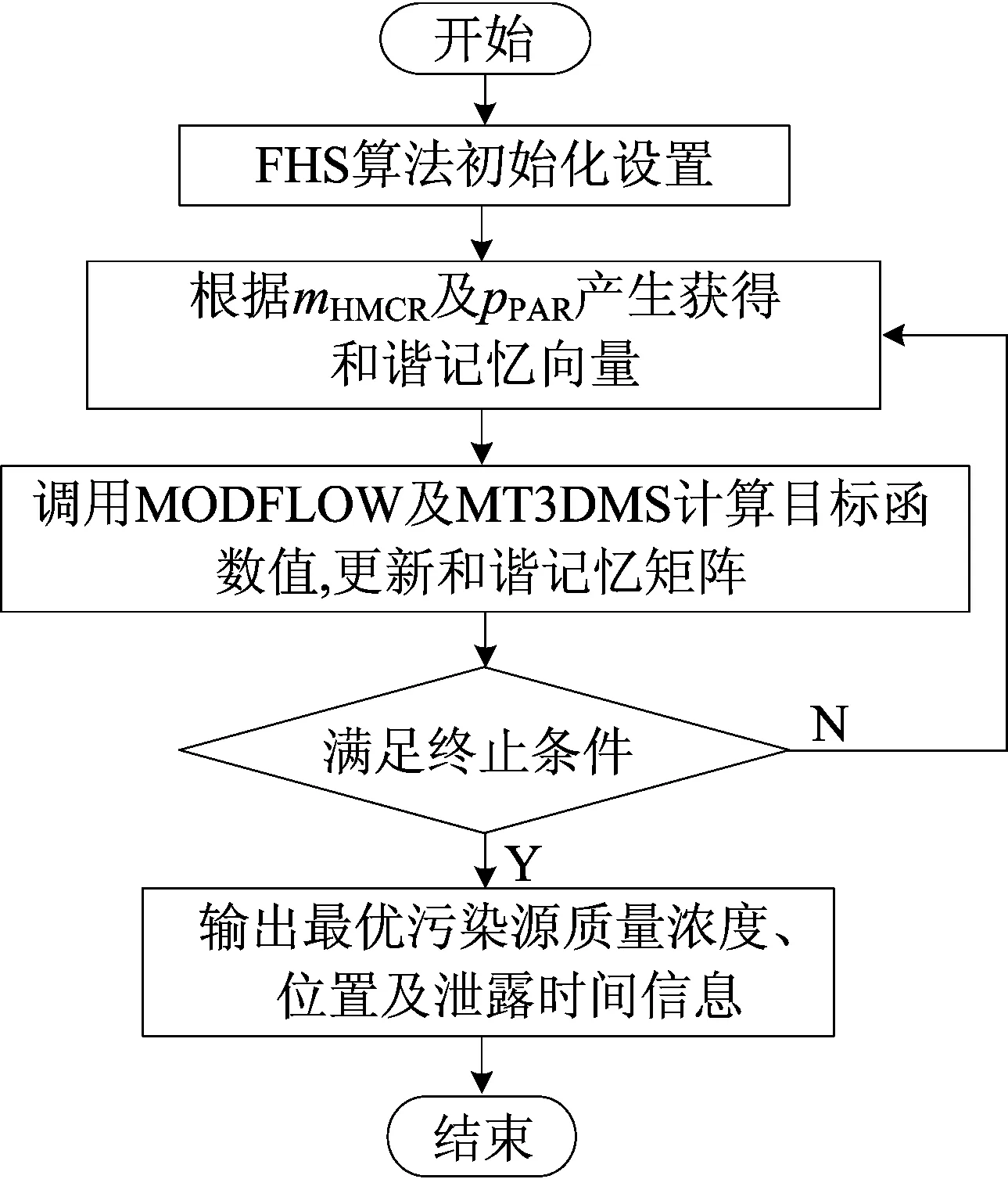
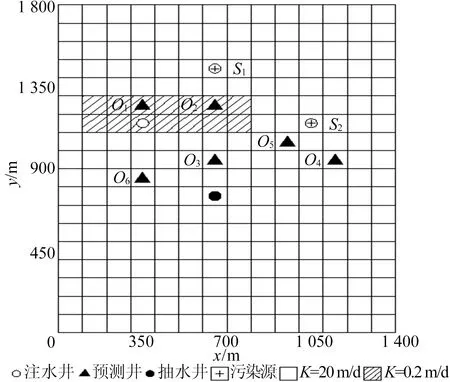
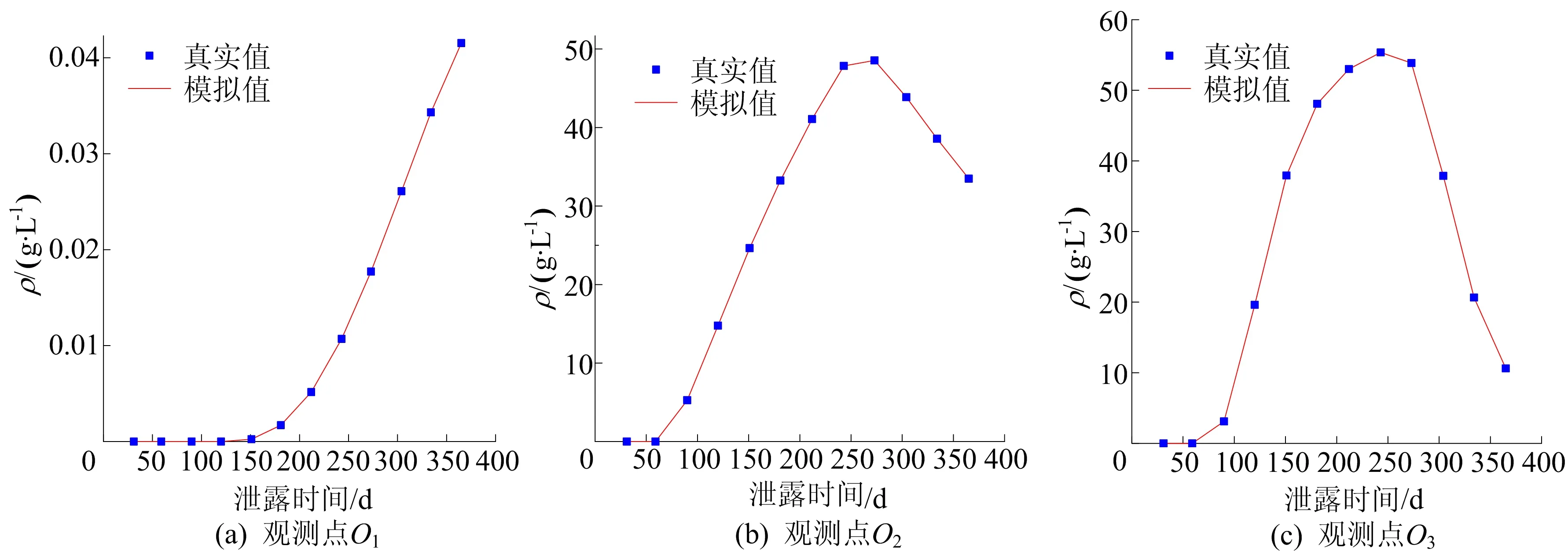
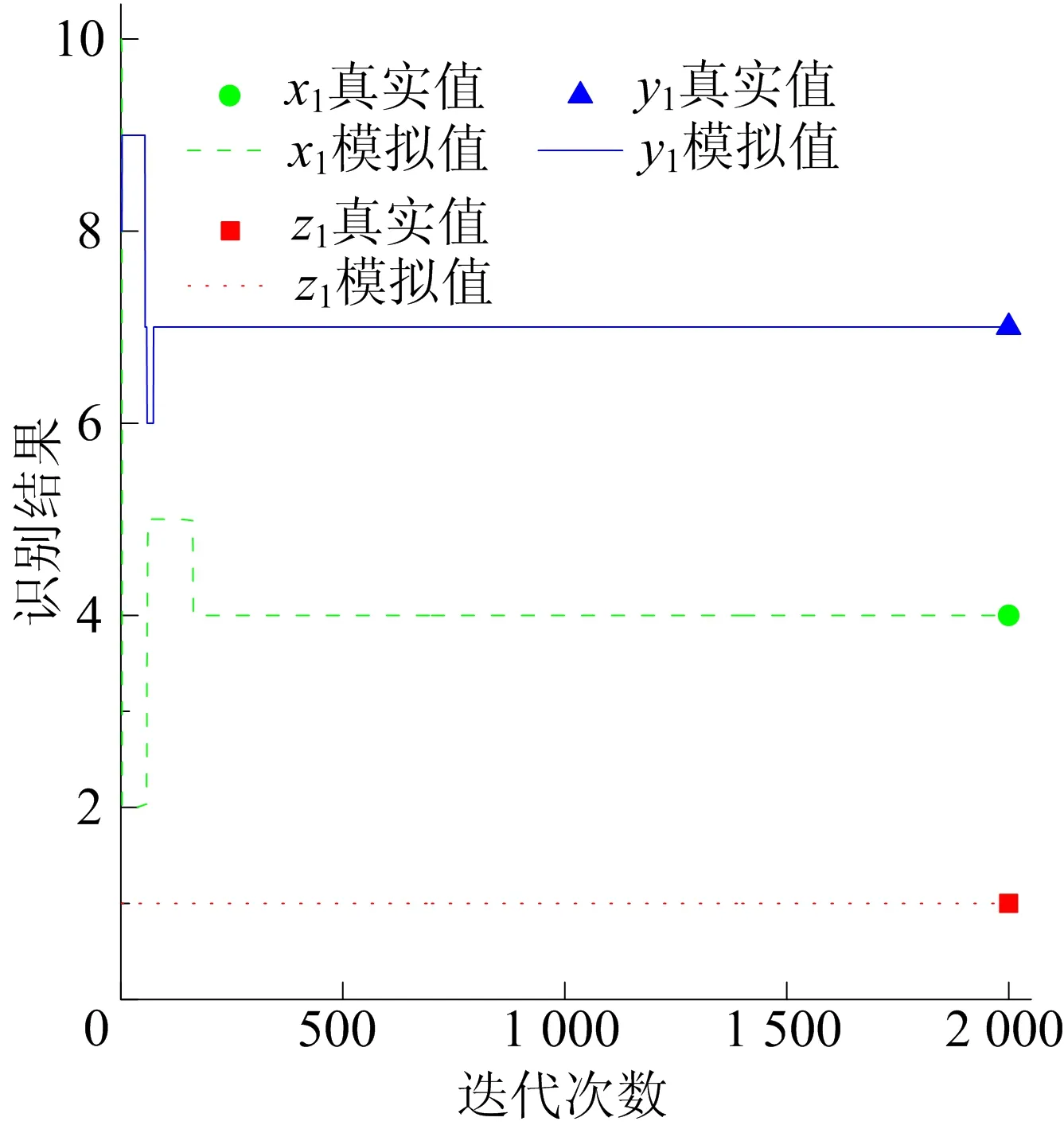
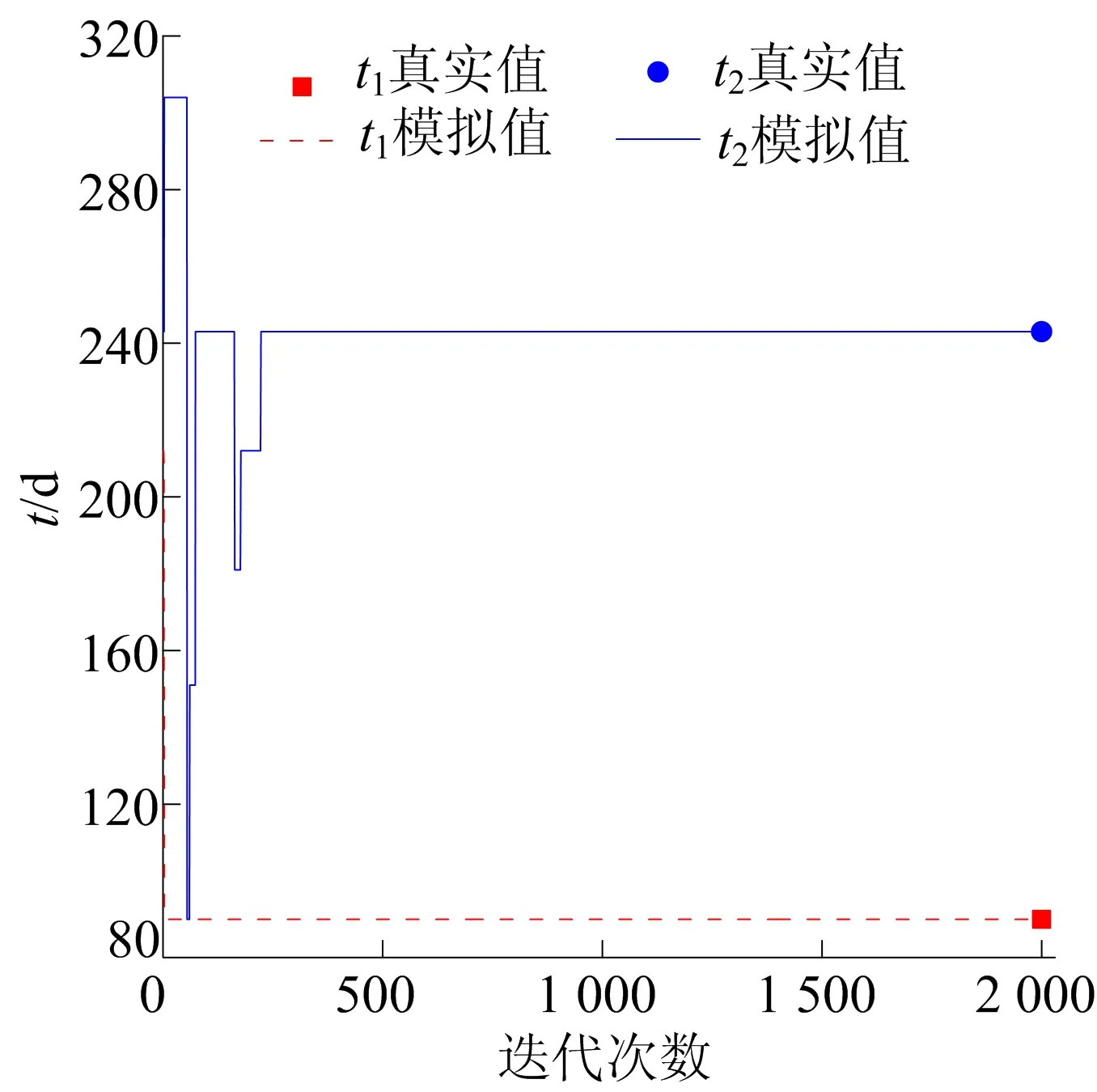
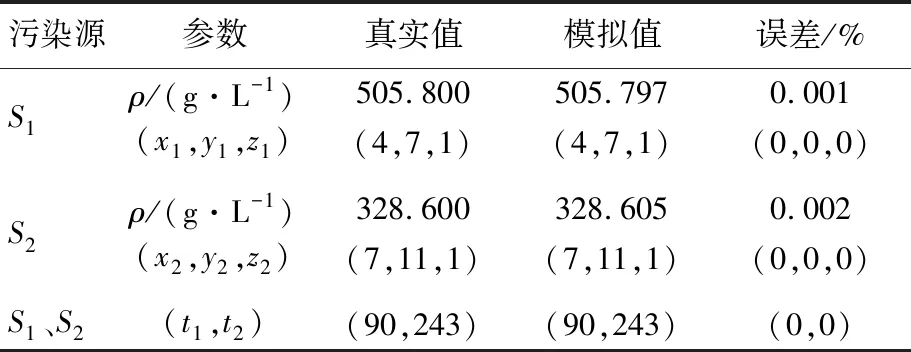
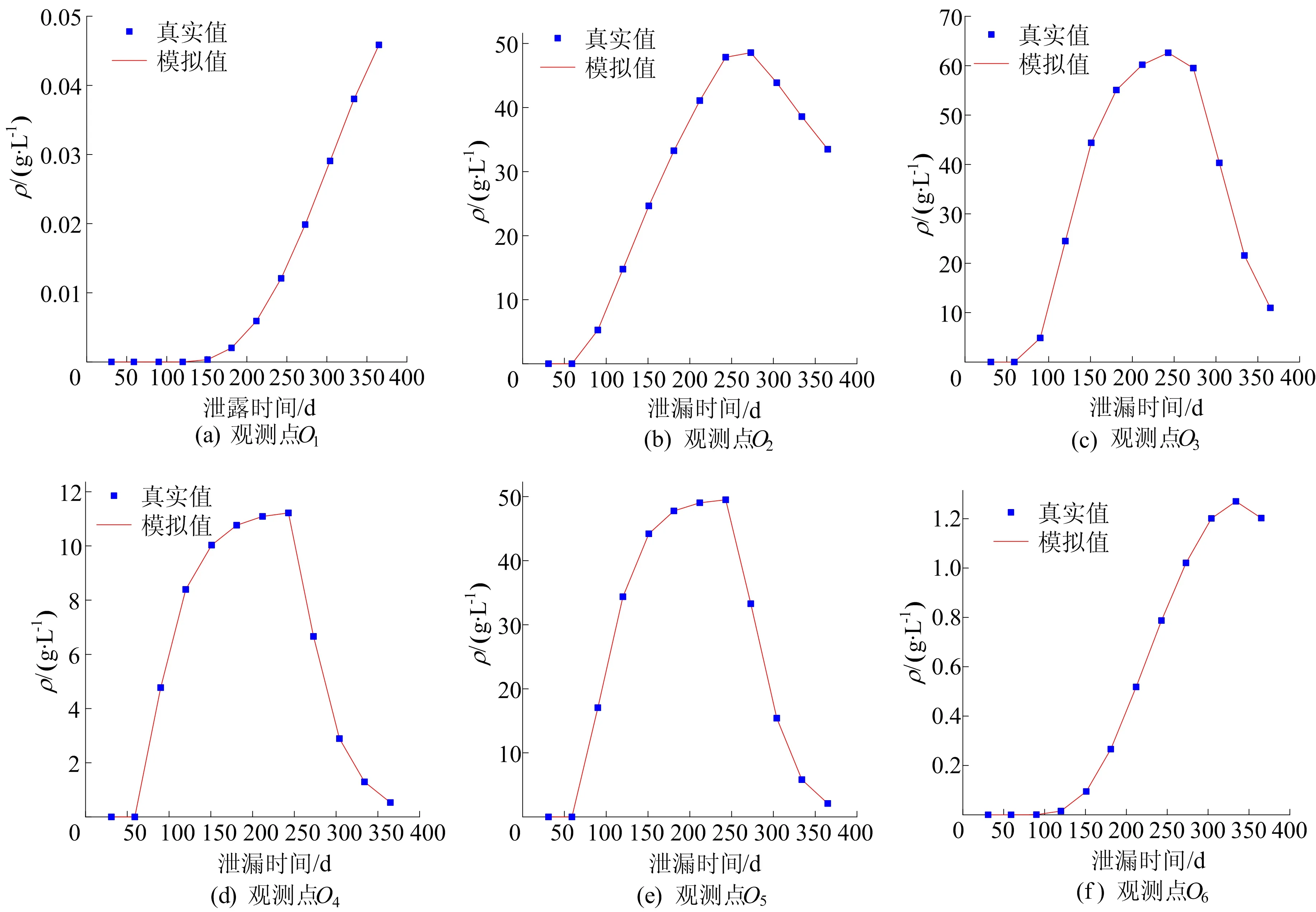
Xmin tmin (4) 1.3.1FHS算法介绍 HS算法是一种基于音乐创作过程的元启发式进化算法。在音乐创作过程中谱写和谐乐章的过程类似于在求解优化问题时寻找最优解的过程。原始HS算法需要依据给定的算法参数和谐记忆存储率(harmony memory considering rate, HMCR)、音阶调整率(pitch adjusting rate, PAR)和带宽来判断生成新的解向量[13]。本文mHMCR和pPAR分别代表和谐记忆存储率和音阶调整率。与原始HS算法相比,FHS算法不需要设置带宽初始值,不再固定pPAR,而是随着算法迭代过程自动调整pPAR值,且新的解向量以上一代中最优解向量为基础生成[15]。因此FHS算法计算效率高于HS算法。 FHS算法主要包括优化问题及算法参数初始化设置、新解向量的生成、和谐记忆矩阵的更新和算法终止条件判断4个步骤。 (1) 优化问题及算法控制参数初始化设置。使用FHS算法进行最优化问题迭代求解之前,首先需要明确最优化问题的目标函数及设置算法控制参数(mHMCR,pPAR,最大迭代步数),生成初始和谐记忆矩阵。和谐记忆矩阵由随机产生的和谐记忆向量及相应的目标函数值构成,即 其中:x=[x1,x2,…,xN]T表示和谐记忆向量,为一组决策变量;N为决策变量的个数;lHMS为和谐记忆长度(规模),表示和谐矩阵中解向量的个数;f(x)为x对应的目标函数值。 (2) 新解向量的生成。通常,生成新解向量x=(x1′,x2′,x3′,…,xN′)需要考虑以下3个准则:① 和谐记忆存储准则(harmony memory consideration),即如果符合此准则,那么新的解向量直接在和谐记忆矩阵中选择生成;② 音节调整准则(pitch adjustment),即用一个接近现有决策变量的值进行替换生成新的解向量;③ 随机生成准则(random selection),即新的解向量在参数取值范围内随机生成。 生成新的解向量时,首先依据和谐记忆存储准则形成新的解向量,程序段如下: 其中,xi′为随机选取的解向量。 若新的解向量是在和谐记忆矩阵中产生,则需要根据音阶调整准则对新产生的解向量进行进一步调整,FHS算法的音节调整程序段如下所示: (3) 更新和谐记忆矩阵。将新生成的解向量所对应的目标函数值与和谐记忆矩阵中最差的目标函数值进行比较,如果新的目标函数值较优,那么用新形成的解向量替换掉和谐记忆矩阵中最差的目标函数值及对应的解向量。 (4) 算法终止条件判断。FHS算法终止条件为达到算法设置的最大迭代步数。若算法达到了最大迭代步数即满足终止条件,则输出优化结果,终止程序,否则算法在步骤(2)~步骤(4)之间循环,直到满足终止条件。 1.3.2 地下水污染源识别模拟优化耦合模型 本文通过将MODFLOW和MT3DMS改写为子程序嵌入到FHS主程序中实现地下水污染源识别模拟模型和优化模型的耦合。基于FHS算法的污染源识别模拟-优化模型求解过程如图1所示。 图1 基于FHS算法求解污染源识别模拟优化模型流程 具体步骤如下:① 对FHS算法的参数进行初始化设置,给定污染源质量浓度、位置和泄露时间取值范围;② 依据mHMCR及pPAR产生新的和谐记忆向量;③ 调用MODFLOW和MT3DMS模拟软件,利用建立的模拟-优化模型计算目标函数值及更新和谐记忆矩阵;④ 判断是否满足算法终止条件的要求,若不满足,则返回步骤② 继续进行迭代计算;⑤ 输出地下水污染源识别结果,包括污染源的质量浓度、位置和泄露时间信息。 研究区为长1 800 m、宽1 400 m的非均质承压含水层,用边长为100 m的正方形网格剖分为18行14列。研究区南北为定水头边界(水头值分别为250、60 m),东西为隔水边界,地下水流为稳定流。研究区内布置有2口注水井、1口抽水井和6口观测井,其中注水井注水量为900 m3/d,抽水井抽水量为1 800 m3/d。含水层的渗透系数K及抽水井、注水井和观测井的分布如图2所示。 图2 研究区污染源、渗透系数、抽注水井及观测井位置分布 设研究区内存在一个或多个污染源,分别通过MODFLOW和MT3DMS模拟软件进行正演计算,获得6个观测井每个月末的质量浓度值为观测真实值用于污染源识别,观测时间为1 a。 假定研究区存在一个未知质量浓度、位置和泄露时间的污染源S1(x1,y1,z1)持续泄露,且泄露时间从t1时刻开始至t2时刻结束,利用建立的污染源识别模拟-优化模型,采用FHS算法识别污染源S1的质量浓度、位置和泄露时间。 优化过程中FHS算法参数设置如下:lHMS=20,mHMCR=0.7,pPAR最小值和最大值分别为0.10、0.99,最大迭代次数为2 000。污染源S1质量浓度、位置和泄露时间识别结果见表1所列。 表1 污染源S1质量浓度、位置和泄露时间识别结果 从表1可以看出,FHS算法可以准确识别出污染源S1的质量浓度、位置(坐标值)及泄露时间,识别结果的误差均为0。 不同观测点处污染物质量浓度识别结果与观测值对比如图3所示。从图3可以看出,不管是处于低渗透区的观测点还是处于高渗透区的观测点,污染物质量浓度的识别结果均与各点处的质量浓度观测值相吻合。 图3 单个污染源不同观测点处污染物浓度识别结果 污染源位置、泄露初始时刻和结束时刻的识别过程分别如图4和图5所示,从图4、图5可以看出,FHS算法经过163次迭代计算就能准确识别出真实污染源的位置,经过223次迭代计算即可准确识别真实污染源的泄露时间段。因此,FHS算法可以高效准确识别单个污染源泄露的相关信息。 图4 污染源S1位置识别过程 图5 污染源S1泄露时间识别过程 假定研究区存在2个未知质量浓度、位置和泄露时间的污染源S1(x1,y1,z1)和S2(x2,y2,z2)持续泄露,且泄露时间从t1时刻开始至t2时刻结束,利用建立的污染源识别模拟-优化模型,采用FHS算法识别污染源S1和S2的质量浓度、位置和泄露时间。 优化过程中FHS算法参数设置除最大迭代次数为10 000,其余与单个污染源信息识别时的设置一致。污染源S1和S2质量浓度、位置和泄露时间识别结果见表2所列。 表2 污染源S1和S2质量浓度、位置和泄露时间识别结果 从表2可以看出,存在2个污染源与只存在单个污染源时识别结果类似,FHS算法可以准确识别出污染源S1和S2的质量浓度、位置(坐标值)及泄露时间,其中质量浓度识别结果的误差分别为0.001%和0.002%,位置和泄露时间识别结果的误差均为0。 不同观测点处污染物质量浓度识别结果与观测值对比如图6所示。 从图6可以看出,不同观测点处污染物质量浓度的识别结果均与观测值相吻合。多个污染源S1、S2位置和泄露时间识别过程与单个污染源S1位置和泄露时间识别过程类似,FHS算法经过5 717次迭代计算即可准确识别出真实污染源的位置信息,经过4 419次迭代计算即可准确识别真实污染源的泄露时间段。 此外,与只存在单个污染源S1的单个污染源信息识别相比,在多个污染源信息识别中由于污染源S2的增加,图6中任意一点污染物质量浓度识别结果总是大于或等于图3中对应相同观测点处相同时刻污染物质量浓度识别结果。 从图6和图3图形的峰值也可以看出,图6d和图6e峰值分别远大于图3d和图3e,说明观测点O4与观测点O5获得的质量浓度模拟值受污染源S2的增加影响较大,符合污染物运移规律,同时也验证了污染源识别结果的正确性与本文方法的可靠性。 图6 多个污染源不同观测点处污染物浓度识别结果 本文将FHS算法与MODFLOW软件和MT3DMS软件相结合,建立污染源识别模拟-优化模型,并将其成功应用于求解单个或多个污染源同时存在等不同情况下污染源识别问题。算例求解结果表明,FHS算法可以准确高效识别含水层参数确定条件下的地下水污染源信息。然而实际含水层参数往往具有不确定性,本文求解方法不能直接应用于求解不确定条件下地下水污染源识别问题;若要求解该问题,则需对FHS算法进行进一步改进,并加入由含水层参数不确定性造成的目标函数不确定性的处理方法。这也是基于FHS算法对地下水污染源信息进行识别的下一步研究计划。
1.3 地下水污染源识别模型耦合及求解
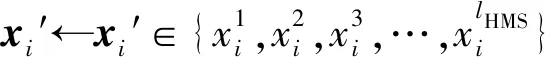
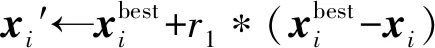
2 算例研究
2.1 算例介绍
2.2 单个污染源信息识别

2.3 多个污染源信息识别
3 结 论
