基于塑性变形的煤体损伤本构关系及渗透率模型研究

2022-01-04吴学海李波波李建华

煤田地质与勘探 2021年6期

吴学海，李波波,2,3，王新，高政，李建华，许江

吴学海1，李波波1,2,3，王新4，高政1，李建华1，许江5

(1. 贵州大学矿业学院，贵州贵阳 550025；2. 贵州大学喀斯特地区优势矿产资源高效利用国家地方联合工程实验室，贵州贵阳 550025；3. 贵州省非金属矿产资源综合利用重点实验室，贵州贵阳 550025；4. 毕节中城能源有限责任公司，贵州毕节 552109；5. 重庆大学煤矿灾害动力学与控制国家重点实验室，重庆 400044)

开采扰动诱发的煤与瓦斯突出是煤矿生产过程中的主要瓦斯动力灾害之一。为系统探索开采扰动下煤体损伤演化特征和瓦斯渗流规律，拟开展不同瓦斯压力下全应力应变–渗流实验。通过考虑气体吸附和热膨胀效应修正广义胡克定律，建立基于塑性变形的煤体损伤本构关系，进一步构建考虑损伤的分段渗透率模型。结果表明：以渗透率突变点为界，可将煤体渗透率分为峰前和峰后2个变化阶段。其中，峰前呈指数型降低，而峰后急剧增加，峰值抗压强度和弹性模量均随着瓦斯压力升高而降低；煤体轴向塑性应变和损伤演化规律具有良好的一致性，二者均呈现出峰前变化不大，峰后激增的变化趋势；利用不同瓦斯压力和50℃实验数据对所建的损伤模型及渗透率模型进行验证，得到理论曲线和实验数据具有较好的吻合度，表明新建模型可较好地反映不同条件下煤体破坏失稳过程中的损伤演化规律和瓦斯渗流特征。

煤与瓦斯突出；塑性变形；损伤；渗透率；开采扰动

煤炭作为三大化石燃料之一，为我国社会经济飞速发展提供有力保障。然而据统计，我国是世界上煤与瓦斯突出事故数量最多、规模最大、损失最严重的国家，安全、高效和绿色是煤矿生产呼吁的主题[1]。地应力、瓦斯压力和温度等因素影响煤体物理力学性质，且这种影响程度随开采深度的增加而增加，使得深部开采下煤体力学响应规律变得更为复杂[2]。此外，开采扰动是造成煤与瓦斯突出事故的根本原因[3]。因此，掌握开采扰动下工作面前方煤体渐进损伤过程和瓦斯运移规律，并建立相关损伤本构关系和渗透率模型，对于实现煤矿安全生产具有重要现实意义。

卸压开采作用使得煤体从原始的三向受力转变为两向受力状态，上覆岩层移动而引起的应力重分布导致垂直方向的支承应力增加而水平方向的应力减少，这种偏应力的增加诱发了煤体损伤、局部破坏和失稳[3-4]。损伤是细观结构在外加荷载作用下出现缺陷，而导致结构劣化的过程[5]。对于损伤的建模很多，其中连续介质损伤力学基于宏观变量描述微观变化来研究材料损伤过程，得到广大研究者的青睐。Xu Xiaoli等[6]基于Weibull分布和Lemaitre应变等效原理，建立花岗岩力热耦合损伤本构模型。张慧梅等[7]分析了岩石冻融损伤特征，并建立基于残余强度特征的岩石损伤本构模型。Jiang Changbao等[8]为了降低煤样离散性的影响，提出用孔隙率和信息熵变化率来表征损伤。Zhu Wancheng等[9]认为当岩石的应力状态满足最大拉应力准则时，发生拉伸破坏，当满足莫尔－库仑准则时，发生剪切破坏，并基于岩石细观非均质性的认识建立煤体分段损伤模型。另外，考虑损伤的本质是材料内部产生不可逆的塑性变形，一些研究者从塑性应变角度出发构建大量的损伤模型，并通过数值模拟对模型进行验证[10-11]。然而在其塑性应变计算中并未考虑到瓦斯压力和温度的影响。瓦斯压力和温度诱导煤体力学性质弱化而产生损伤已得到广泛研究。首先在瓦斯方面，刘力源等[12]认为气体吸附诱发基质产生细观损伤，弹性模量和强度均随着瓦斯压力的升高而降低。Wang Hanpeng等[13]从细观角度出发，认为瓦斯吸附产生的膨胀效应会削弱煤体颗粒接触黏结力，从而导致煤体力学性质劣化。在温度方面，尹光志[14]、Wang Chunguang[15]等认为温度升高，煤体三轴抗压强度和承受变形能力减小。Teng Teng等[16]认为温度不仅会造成煤体出现热膨胀，还会引起热损伤和热裂等。归纳以上研究成果不难发现，损伤在岩石领域具有丰硕的研究成果，而在煤体研究方面大多停留在实验分析阶段，相关损伤理论亟待深入研究。

渗透率是控制煤中瓦斯流动的重要参数，其大小与煤裂隙尺寸、密度以及连通性密切相关[17]。对于渗透率模型研究由来已久，早在1987年，I. Gray[18]以火柴棍几何模型为基础，建立煤体单轴应变条件下的渗透率模型。随后，Shi J.Q.等[19]将孔隙压力变化转化为有效应力变化，通过引入裂隙压缩性系数提出了渗透率模型(S-D模型)。然而，这些经典的渗透率模型主要基于单轴应变条件进行建模。在开采扰动下，Zhou Hongwei等[20]提出了一种分数阶导数渗透率模型，建立煤体峰后损伤和渗透率之间的内在联系。Xue Yi等[4]通过不同加卸载路径研究了煤体力学行为及渗透率演化规律。

综上所述，在开采扰动作用下，从塑性变形角度出发，考虑瓦斯压力和温度影响下的煤体损伤演化机制研究较少，同时有关工作面前方煤层瓦斯运移规律的理论研究也较少。鉴于此，为厘清瓦斯压力影响下的煤体损伤演化机制和瓦斯流动行为，拟开展不同瓦斯压力条件下全应力应变–渗流实验。在理论创新上，通过考虑气体吸附和热膨胀效应修正广义胡克定律，建立基于塑性变形的煤体损伤本构关系，进一步构建考虑损伤的分段渗透率模型。利用实验结果与笔者前期开展的高温条件的煤体全应力应变–渗流实验数据对新建模型进行验证，以期为煤矿瓦斯灾害防治提供理论指导。

1 损伤－渗透率模型构建

首先进行较合理假设：

①煤是一种均质的且各向同性的弹性介质；

②裂隙提供了瓦斯气体的渗流通道；

③吸附/解吸遵循Langmuir等温吸附，且可逆；

④瓦斯在煤中的流动遵循达西定律。

1.1 损伤本构模型

在开采扰动下，工作面前方的应力集中处是煤体损伤快速发育区域。同时，煤层中瓦斯压力变化以及埋深增加导致的温度升高均不同程度地造成煤体损伤，宏观上表现为煤体弹性模量不断降低[13]。假设损伤破裂过程是连续的，则弹性模量的演化规律可以表示为：

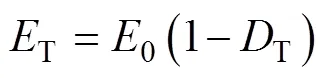
式中：p为瓦斯压力为时的弹性模量，MPa；T为温度时的弹性模量，MPa；p为瓦斯气体诱导损伤(以下简称气体损伤)；T为温度效应引起的损伤(以下简称热损伤)；下标0表示初始状态。

煤在长时间经历复杂的地质构造作用后，其内部将存在许多孔洞和缺陷(损伤)。煤体力学性质也因孔洞和缺陷的数量、大小以及不均匀的分布特点而有所差异。曹文贵等[21]将煤体划分为许多足够小的微元，每个微元里包含着这些缺陷，随着所处应力状态的改变，微元随机破坏，并假设煤体微元强度服从Weibull函数分布，从而推导出煤体统计损伤本构关系。然而，在其本构关系中，微元强度代表了数学中一个概率参数。在应力加载下，煤体中不断萌生新的微裂纹，损伤单元的数量不断增加。换言之，煤体塑性变形持续变大。假设损伤概率与塑性应变相关且服从Weibull函数分布，应力改变下煤体荷载损伤变量[10]可以表示为：

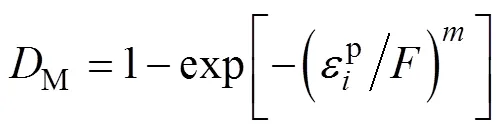
假设瓦斯压力和温度对煤体造成的损伤在应力加载前均已完成，将二者损伤之和定义为外部损伤，表示为：

式中：N为外部损伤。

外部损伤和荷载损伤之间存在相互耦合关系，总损伤[6]并非是简单的二者叠加，而是表示为：

式中：tol为总损伤变量；为荷载损伤修正系数。

将式(1)—式(4)代入式(5)得到总损伤变量表达式为：

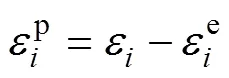
无论是在开采扰动还是在室内进行实验时，随着应力水平的提高，煤体将经历弹塑性变形过程。在弹性变形阶段，煤体弹性应变往往通过广义胡克定律[22]进行表征：

式中：为弹性模量，MPa；为泊松比；σ、σ、σ分别为、、方向上的应力，MPa。

然而，式(8)中弹性应变是应力变化所致，忽略了瓦斯压力和温度对其造成的影响。笔者认为瓦斯压力和温度变化除了导致煤体产生损伤之外，吸附/解吸和热胀冷缩作用还会使得弹性应变有所劣化。因此，考虑吸附变形、热膨胀变形和瓦斯引起的力学作用，修正广义胡克定律为：

式中：为孔隙压力，MPa；为Biot系数；s为吸附应变；Te为热膨胀应变。

假设煤体膨胀是各向同性，吸附变形[23]可以表示为：

式中：L为Langmuir吸附体积应变常数；L为Langmuir吸附压力常数，MPa；1为入口瓦斯压力，MPa。

温度变化引起的热膨胀变形[24]可以表示为：

在假三轴实验中，

式中：Δ为偏应力，MPa；1、3分别为轴压和围压，MPa。

根据Lemaitre应变等价假说[25]，煤体损伤本构关系可以表示为：

在实验过程中，为了简化研究，取轴向为研究对象，同时Biot系数取值为1，将式(1)、式(2)、式(6)代入式(13)得到基于塑性变形的煤体损伤本构关系为：

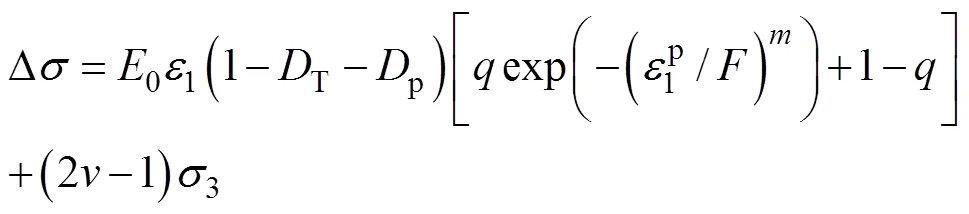
1.2 渗透率模型

渗透率模型实质上是描述煤体中瓦斯渗流规律的本构方程，构建渗透率模型是评价瓦斯抽采效果、计算开采扰动下工作面瓦斯涌出量的前提。荣腾龙等[26]通过对比指数型和立方型渗透率模型得出，指数型渗透率模型有更好的拟合优度。鉴于此，笔者拟用有效应力表征的指数型渗透率模型进行建模，其基础本构关系[19]为：

式中：为渗透率，10–3μm2；f为裂隙压缩性系数，MPa–1；e为有效应力，MPa；下标0表示初始状态。

其中，有效应力[27]可以表示为：

式中：eff为有效围压，MPa，且eff=3–。

裂隙压缩性系数反映了煤体孔裂隙结构可被压缩的难易程度。为了在所提出的渗透率模型中考虑瓦斯压力和温度对裂隙压缩性系数的影响，定义裂隙压缩性系数为：

式中：为裂隙压缩性系数修正因子，反映温度和瓦斯压力变化引起裂隙发育的敏感程度。

将式(17)代入式(15)得到考虑气体损伤和热损伤的渗透率模型为：

Zhu Wancheng等[28]在幂函数中加入指数项，以反映煤体屈服后损伤对渗透率的贡献。然而需要注意的是，在其建模的过程中，采用了立方型渗透率模型与损伤进行耦合，模型推导过程较为复杂。因此，本文尝试在指数函数的渗透率模型中加入指数项(荷载损伤)，建立峰后考虑损伤的渗透率模为：

式中：1为峰前渗透率最低值，10–3μm2；k为损伤对渗透率的影响系数。

结合式(18)和式(19)得到考虑损伤的分段渗透率模型为：

式中：c0为渗透率突变点的轴向应变。

2 实验方法

2.1 煤样制备

实验煤样取自山西晋城赵庄矿3号煤层，该煤层为无烟煤，且属于质地坚硬的原生结构类型。相较于碎粒、糜棱结构的煤来说，原生结构煤透气性较好[29]。通过现场实际考察知该煤层瓦斯压力较大，为突出煤层。因此，该煤样可较好地反映式(9)中吸附应变对弹性变形的影响。

煤样的制作过程：首先，将现场取来煤样放置于大小合适的木箱内。其次，用细骨料混凝土浇筑煤块与木箱之间的间隙，以固定煤块，防止煤块晃动导致取心失败。最后，待混凝土硬化完全后，用取心机钻取煤样，随后用磨床将取出的煤心加工成直径为50 mm，长度为100 mm的圆柱形试件。本实验采用自主研发的含瓦斯煤热–流–固耦合三轴伺服渗流实验装置[30]。

2.2 实验方案

为模拟煤体在应力环境改变过程中力学响应和瓦斯流动特征，同时考虑开采扰动时工作面前方煤层瓦斯压力的变化。以CH4作为实验气体，恒定围压为2.0 MPa，恒定温度为30 ℃，开展瓦斯压力为0.5、1.0和1.5 MPa下的全应力应变–渗流实验，控制出口端瓦斯压力为0.1 MPa。实验步骤如下。

基于CMOS平台的硅光子关键器件与工艺研究………………………………赵瑛璇，武爱民，甘甫烷 24-4-08

①试件安装：采用704硅橡胶均匀地抹在试件侧面，待胶层完全干透之后，将试件安置于三轴压力室的底座上，然后连接好各种辅助设备。

②真空脱气：打开出气阀门，在保证容器气密性良好的情况下对试件进行真空脱气。

③实验条件设定：真空脱气结束后关闭出气阀门，调节三轴压力室。置于恒温水浴中并设定温度为30 ℃，采用力控制的方式以0.5 MPa的梯度依次交替加载轴压、围压至2 MPa。

④煤样吸附：打开进气阀门，控制瓦斯压力恒为0.5 MPa，向试件内持续充气，并在吸附24 h后的连续2 h内检测到压差波动不超过0.01 MPa，此时认为达到吸附平衡。

⑤以速度为0.1 mm/min方式施加轴压至试件破坏。

数据记录完成后，更换试件，重复实验步骤①—⑤进行瓦斯压力为1.0、1.5 MPa的全应力应变–渗流实验。需要注意的是：为了保证实验的可重复性，在每个瓦斯压力点下进行3次平行实验，然后从中选取1个煤样实验结果进行分析。根据实验测得的瓦斯流量，利用达西定律计算煤体渗透率[31]。

3 实验结果分析及模型验证

3.1 实验结果分析

通过不同瓦斯压力下全应力应变–渗流实验，得到煤体应力、渗透率与应变的变化关系如图1所示。

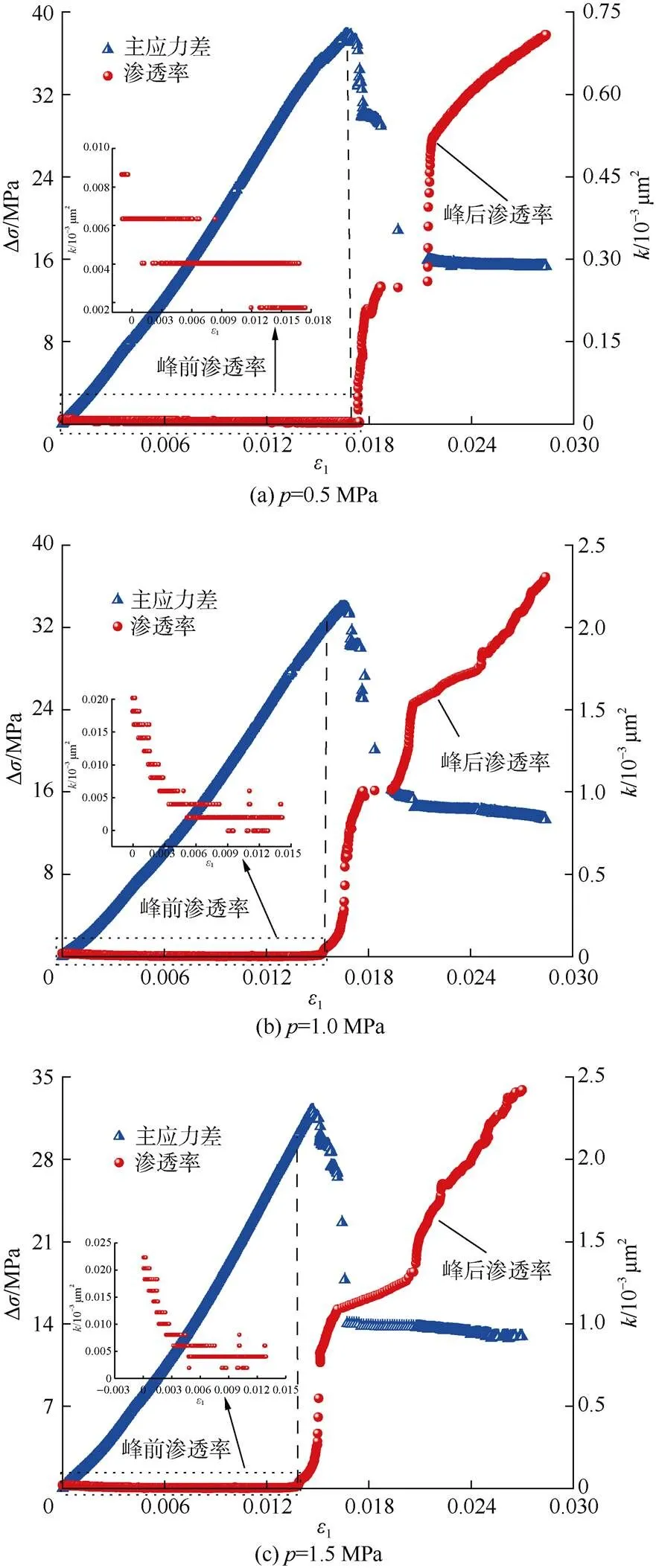
图1 不同瓦斯压力下煤体应力、渗透率与应变的变化关系

1) 峰前阶段

为准确描述煤体变形破坏前力学性质的变化机制，进一步将峰前阶段划分为压密阶段、弹性变形阶段和塑性屈服阶段。其中：在压密阶段，应力应变曲线出现细微的弯折现象，切线斜率(弹性模量)略微提升，这是由于煤中原始孔裂隙被压密压实而使得细观缺陷得到改善，从而使得其强度有所提高。在弹性变形阶段，煤中孔裂隙继续被压实，应力应变曲线近似线性关系。在塑性屈服阶段，煤体内部逐渐萌生新的微裂纹并在轴向应力的持续加载下不断发育、扩展。此时，由于塑性应变的产生使得煤体出现非线性的变形行为，应力应变曲线切线斜率(弹性模量)逐渐降低，煤体内损伤也在逐渐累积。由图1不难发现渗透率在峰前持续降低，这是因为此阶段内煤体内部孔裂隙被压密压实，甚至闭合，导致瓦斯流动通道变窄。值得注意的是：理论上，煤体发生塑性屈服后，渗透率便会提升。但由于煤体脆性特征过于显著，使得屈服点接近于峰值点。此外，瓦斯在煤体内部流动的变化规律并非一蹴而就，存在明显的滞后效应[32]，因此，煤体渗透率呈现出降低趋势。另外，在图1中此阶段渗透率之所以呈现阶梯性的降低现象，是因为初始的渗透率值太小，流量计难以鉴别这细微的变化，但这并不影响对峰前阶段渗透率总体演化规律的评价。

2) 峰后阶段

此阶段煤体已发生宏观破坏，同理可将其划分为应力跌落阶段和残余强度阶段。在应力跌落阶段，由于裂纹扩展至相互贯通，形成宏观裂缝使得煤体失去部分承载能力，出现应力跌落现象。与此同时，渗透率急剧升高。在残余强度阶段，由于摩擦和围压的相互作用使得煤体在破坏后仍具有一定的承载能力，而断裂面凹凸部分在应力的加载下被磨损或剪断并进一步被压密闭合，因此，造成渗透率在残余强度阶段提升幅度略有降低。

此外，在煤炭回采过程中，工作面瓦斯的涌出使得储层压力降低，进一步导致煤体力学性质和瓦斯渗透特性发生改变。由图1可知：随着瓦斯压力增大，煤体峰值抗压强度降低，而初始渗透率呈升高的变化趋势。究其原因，随着瓦斯压力的增大使得煤体孔裂隙中的吸附瓦斯和游离瓦斯含量增加。一方面，煤中的气体吸附被认为是一种受范德华力控制的物理现象[33]，吸附过程中产生的能量消耗使得煤体颗粒间的黏结力降低；另一方面，游离瓦斯含量的增加降低了有效围压，使得煤体中孔裂隙得到一定程度的发育。二者共同诱发了煤体损伤，因此，宏观上表现为煤体峰值强度随瓦斯压力的增大而降低，而初始渗透率呈相反的变化趋势。

3.2 模型验证

3.2.1 损伤模型

无论是工作面瓦斯涌出还是瓦斯抽采都会导致煤储层瓦斯压力变化，进一步导致煤体力学性质产生变化。由于文献[30]中的实验煤样与本文实验煤样属于同一批煤样，因此，可从文献[30]直接得到式(14)中热损伤T=0.007。并利用不同瓦斯压力下全应力应变实验数据，代入式(14)得到理论曲线如图2所示，同时，将实验数据代入式(9)和式(7)求得不同瓦斯压力下轴向塑性应变，进一步将其代入式(6)可得损伤变量变化值。

由图2可知：理论曲线和实验数据匹配程度高，瓦斯压力为0.5、1.0、1.5 MPa下的2分别为0.99、0.99、0.98，表明基于塑性变形的损伤本构模型可较好地反映不同瓦斯压力下煤体变形破坏特征。此外，不同瓦斯压力下煤体轴向塑性应变和损伤变量演化规律阶段特征基本相似，总体上呈现“S”形变化趋势。以瓦斯压力0.5 MPa为例，在压密阶段煤体中孔裂隙被压实使得轴向塑性应变有所提升。进入弹性变形阶段后，轴向塑性应变呈现略微下降的趋势。而从屈服点开始，由于微裂纹的萌生和发展使得塑性应变先缓慢升高，在峰值破坏后急剧升高。由于煤体损伤的本质是塑性应变的产生，因此二者具有相同的变化趋势，这与Cai Wu等[10]的研究保持良好的一致性。

表1列出了不同瓦斯压力下损伤模型参数，其中不同瓦斯压力下的煤体弹性模量p值为应力应变曲线上弹性变形阶段的斜率，泊松比也为该阶段中径向应变绝对值与轴向应变的比值。有研究指出，煤体弹性模量随着瓦斯压力的升高而降低，且在较低围压下线性降低趋势较为明显[34]。需要注意的是：本文实验的围压为2 MPa(较低)，通过线性拟合得到0=2 233.45 MPa。将0和p值代入式(1)即可求得气体损伤变量p值。

由表1不难看出，煤体弹性模量随着瓦斯压力的升高而降低，而泊松比呈现相反变化趋势。p随着瓦斯压力的增大而增大，进一步表明瓦斯压力对煤体力学性质具有一定的劣损作用。Weibull分布参数、及损伤修正系数对应力应变曲线的影响将在第4节进行论述。

3.2.2 渗透率模型

渗透率模型是定量表征煤体中瓦斯运移的重要数学方程，为了验证考虑损伤的分段渗透率模型的合理性，将不同瓦斯压力下全应力应变–渗流实验数据代入(式(20))，得煤体渗透率理论曲线如图3所示。

图2 不同瓦斯压力下煤体损伤理论曲线与实验数据对比

表1 不同瓦斯压力下煤体损伤模型参数

图3 不同瓦斯压力煤体渗透率理论曲线与实验数据对比

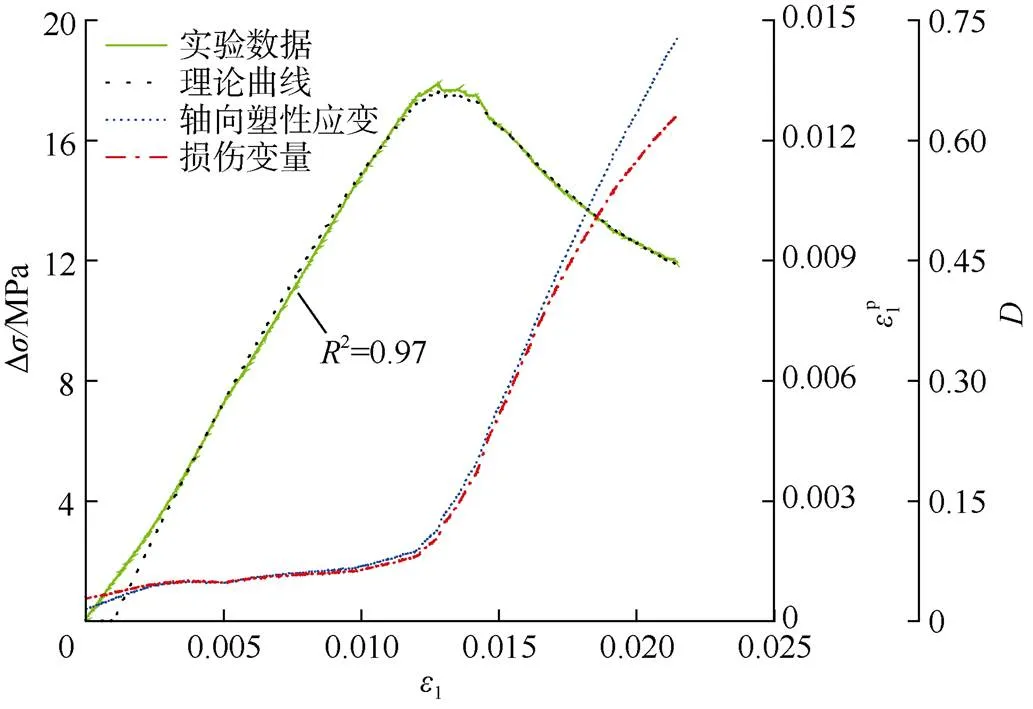
由图3可知：当1

不同瓦斯压力下煤体渗透率模型参数见表2，其中e0、0和1为模型输入参数。

表2 不同瓦斯压力下煤体渗透率模型参数

4 讨论

4.1 损伤模型参数敏感性分析

在3.2.1节中已证明基于塑性变形的损伤本构模型可较好贴合应力应变曲线变化特征，其中参数、和为新建损伤模型的主要参数，可能控制着煤体应力应变曲线演化规律。因此，为鉴别应力应变曲线对于不同参数取值的敏感程度，基于瓦斯压力0.5 MPa下理论曲线(图2a)，通过控制变量法，分别绘制了参数、和对应力应变曲线的影响，结果如图4—图6所示。

图4 参数m对应力应变曲线的影响

图5 参数F对应力应变曲线的影响

图6 参数q对应力应变曲线的影响

由图4不难看出，参数控制着煤体峰值抗压强度和残余强度，值愈大，峰值抗压强度愈大，残余强度愈小，也即脆性特征愈明显。

由图5可知：参数也控制着煤体峰值抗压强度和残余强度，但不同的是，峰值抗压强度和残余强度均随着值增大而增大。同时由图5和图4还可以看出，煤体峰前应力应变曲线斜率(弹性模量)随着参数的增大而增大。参数、所反映的材料力学性质与前人的研究保持良好的一致性[35]。

由图6可知：参数对煤体峰前曲线形状几乎没有影响，却明显地改变了残余强度特征，值愈大，残余强度愈小，表明损伤修正系数主要控制着煤体峰后变形情况。探究参数不同取值情况下应力应变曲线变化规律，可为损伤建模提供参考。

4.2 模型推广

为进一步验证本文所建模型的合理性和适用性，笔者基于前期开展的工作[30]，将温度为50 ℃下煤体全应力应变实验数据代入式(14)得到理论曲线(图7)，其中轴向塑性应变和损伤变量演算方法同上(不同瓦斯压力)。模型相关参数见表3。

图7 50℃下煤体损伤理论曲线与实验数据对比

表3 50℃下煤体损伤模型参数

由图7可知：拟合优度(2)为0.97，表明基于塑性变形所建的煤体损伤本构模型也可较好地反映高温环境下煤体变形破坏特征，尤其在峰后阶段，理论值和实验值保持高度一致性。此外，轴向塑性应变和损伤变量的演化规律与不同瓦斯压力条件下基本一致，即峰前变化平缓，峰后急剧增加，进一步说明塑性变形、损伤演化与煤中裂纹发育情况息息相关。

同理，为了验证高温条件下渗透率模型(式(20))的合理性，将温度为50 ℃下煤体全应力应变–渗流实验数据代入其中，分别得到峰前和峰后的理论曲线如图8所示。其中，渗透率模型参数见表4。

图8 50℃下煤体渗透率理论曲线与实验数据对比

由图8可知：无论当1

表4 50℃下煤体渗透率模型参数

综上，通过不同瓦斯压力和50 ℃条件下实验数据对比，验证了基于塑性变形的损伤本构关系及考虑损伤的分段渗透率模型具有良好的合理性。剖析煤体塑性变形—损伤—渗透率的全过程，厘清了开采扰动下煤体力学响应和瓦斯渗流行为，为井下巷道支护设计，瓦斯灾害防治等提供重要的借鉴意义。

然而，煤体隶属于岩石类材料，在塑性状态下，岩土体应力应变关系是非线性的，与应力路径、应力历史、硬化参数选择、加载函数等密切相关[37]。了解煤体变形破坏过程中塑性流动规律是分析煤体弹塑性变形的重要前提，因此，相关理论模型的建立及定量分析，是今后的研究重点。

5 结论

a. 以渗透率突变点为界可将全应力应变–渗流过程分为峰前阶段和峰后阶段。峰前阶段，煤体经历了压密阶段、弹性变形阶段和塑性屈服阶段，渗透率呈指数型降低；峰后阶段，煤体经历应力跌断阶段和残余强度阶段，渗透率急剧升高。瓦斯气体对煤体力学性质具有一定的劣损作用，表现为峰值抗压强度和弹性模量均随着瓦斯压力的升高而降低。

b. 煤体轴向塑性应变和损伤演化规律具有良好的一致性，二者均呈现为峰前变化不大，峰后急剧增加。通过不同瓦斯压力和50 ℃条件下实验数据对比验证了基于塑性变形的损伤本构关系及考虑损伤的分段渗透率模型的合理性，表明新建模型可较好地反映煤体破坏失稳过程中的损伤演化规律和瓦斯渗流特征，可为深部开采提供一定的理论指导。

c. 探究应力应变曲线对损伤本构关系中参数敏感度发现，值愈大，峰值抗压强度愈大，残余强度愈小；峰值抗压强度和残余强度均随着值增大而增大；损伤修正系数主要控制着煤体峰后变形情况。

[1] 张超林，许江，彭守建，等. 煤与瓦斯突出物理模拟实验研究进展及展望[J]. 煤田地质与勘探，2018，46(4)：28–34.

ZHANG Chaolin，XU Jiang，PENG Shoujian，et al. Advances and prospects in physical simulation of coal and gas outburst[J]. Coal Geology & Exploration，2018，46(4)：28–34.

[2] 谢和平，高峰，鞠杨. 深部岩体力学研究与探索[J]. 岩石力学与工程学报，2015，34(11)：2161–2178.

XIE Heping，GAO Feng，JU Yang. Research and development of rock mechanics in deep ground engineering[J]. Chinese Journal of Rock Mechanics and Engineering，2015，34(11)：2161–2178.

[3] 高明忠，王明耀，谢晶，等. 深部煤岩原位扰动力学行为研究[J]. 煤炭学报，2020，45(8)：2691–2703.

GAO Mingzhong，WANG Mingyao，XIE Jing，et al. In-situ disturbed mechanical behavior of deep coal rock[J]. Journal of China Coal Society，2020，45(8)：2691–2703.

[4] XUE Yi，RANJITH P G，GAO Feng，et al. Mechanical behaviour and permeability evolution of gas-containing coal from unloading confining pressure tests[J]. Journal of Natural Gas Science and Engineering，2017，40：336–346.

[5] GUO Hui，GUO Weiguo，ZHAI Yue，et al. Experimental and modeling investigation on the dynamic response of granite after high-temperature treatment under different pressures[J]. Construction and Building Materials，2017，155(30)：427–440.

[6] XU Xiaoli，KARAKUS M. A coupled thermo-mechanical damage model for granite[J]. International Journal of Rock Mechanics and Mining Sciences，2018，103：195–204.

[7] 张慧梅，孟祥振，彭川，等. 冻融－荷载作用下基于残余强度特征的岩石损伤模型[J]. 煤炭学报，2019，44(11)：3404–3411.

ZHANG Huimei，MENG Xiangzhen，PENG Chuan，et al. Rock damage constitutive model based on residual intensity characteristics under freeze-thaw and load[J]. Journal of China Coal Society，2019，44(11)：3404–3411.

[8] JIANG Changbao，YANG Yang，WEI Wenhui，et al. A new stress-damage-flow coupling model and the damage characterization of raw coal under loading and unloading conditions[J]. International Journal of Rock Mechanics and Mining Sciences，2021，138(5)：104601.

[9] ZHU Wancheng，TANG Chun’an. Micromechanical model for simulating the fracture process of rock[J]. Rock Mechanics and Rock Engineering，2004，37(1)：25–56.

[10] CAI Wu，DOU Linming，JU Yang，et al. A plastic strain-based damage model for heterogeneous coal using cohesion and dilation angle[J]. International Journal of Rock Mechanics and Mining Sciences，2018，110：151–160.

[11] WANG Jiachen，WANG Zhaohui，YANG Shengli. A coupled macro-and meso-mechanical model for heterogeneous coal[J]. International Journal of Rock Mechanics and Mining Sciences，2017，94：64–81.

[12] 刘力源，朱万成，魏晨慧，等. 瓦斯吸附诱发煤强度劣化的力学模型与数值分析[J]. 岩土力学，2018，39(4)：1500–1508.

LIU Liyuan，ZHU Wancheng，WEI Chenhui，et al. Mechanical model and numerical analysis of mechanical property alterations of coal induced by gas adsorption[J]. Rock and Soil Mechanics，2018，39(4)：1500–1508.

[13] WANG Hanpeng，LIU Zhongzhong，YUAN Liang，et al. Experimental test and particle mechanical analysis of gas adsorption-induced coal rock degradation[J]. Powder Technology，2020，362：75–83.

[14] 尹光志，蒋长宝，许江，等. 含瓦斯煤热流固耦合渗流实验研究[J]. 煤炭学报，2011，36(9)：1495–1500.

YIN Guangzhi，JIANG Changbao，XU Jiang，et al. Experimental study of thermo-fluid-solid coupling seepage of coal containing gas[J]. Journal of China Coal Society，2011，36(9)：1495–1500.

[15] WANG Chunguang，FENG Jili，LIU Jishan，et al. Direct observation of coal-gas interactions under thermal and mechanical loadings[J]. International Journal of Coal Geology，2014，131：274–287.

[16] TENG Teng，WANG Jianguo，GAO Feng，et al. A thermally sensitive permeability model for coal-gas interactions including thermal fracturing and volatilization[J]. Journal of Natural Gas Science and Engineering，2016，32：319–333.

[17] RAMANDI H L，MOSTAGHIMI P，ARMSTRONG R T. Digital rock analysis for accurate prediction of fractured media permeability[J]. Journal of Hydrology，2017，554：817–826.

[18] GRAY I. Reservoir engineering in coal seams：Part 1. The physical process of gas storage and movement in coal seams[J]. SPE Reservoir Engineering，1987，2(1)：28–34.

[19] SHI Jiquan，DURUCAN S. Drawdown induced changes in permeability of coalbeds：A new interpretation of the reservoir response to primary recovery[J]. Transport in Porous Media，2004，56(1)：1–16.

[20] ZHOU Hongwei，ZHAO Jiawei，SU Teng，et al. Characterization of gas flow in backfill mining-induced coal seam using a fractional derivative-based permeability model[J]. International Journal of Rock Mechanics and Mining Sciences，2021，138：104571.

[21] 曹文贵，赵明华，刘成学. 基于Weibull分布的岩石损伤软化模型及其修正方法研究[J]. 岩石力学与工程学报，2004，23(19)：3226–3231.

CAO Wengui，ZHAO Minghua，LIU Chengxue. Study on the model and its modifying method for rock softening and damage based on Weibull random distribution[J]. Chinese Journal of Rock Mechanics and Engineering，2004，23(19)：3226–3231.

[22] 刘之喜，王伟，罗吉安，等. 岩石单轴压缩试验中能量演化分析方法[J]. 煤炭学报，2020，45(9)：3131–3139.

LIU Zhixi，WANG Wei，LUO Ji’an，et al. Method of energy evolution of rock under uniaxial compression test[J]. Journal of China Coal Society，2020，45(9)：3131–3139.

[23] WANG Zhiming，SUN Yuning，WANG Yonglong，et al. A coupled model of air leakage in gas drainage and an active support sealing method for improving drainage performance[J]. Fuel，2019，237：1217–1227.

[24] 李波波，高政，杨康，等. 考虑温度、孔隙压力影响的煤岩渗透性演化机制分析[J]. 煤炭学报，2020，45(2)：626–632.

LI Bobo，GAO Zheng，YANG Kang，et al. Analysis of coal permeability evolution mechanism considering the effect of temperature and pore pressure[J]. Journal of China Coal Society，2020，45(2)：626–632.

[25] LEMAITRE J. How to use damage mechanics[J]. Nuclear Engineering and Design，1984，80(3)：233–245.

[26] 荣腾龙，周宏伟，王路军，等. 三向应力条件下煤体渗透率演化模型研究[J]. 煤炭学报，2018，43(7)：1930–1937.

RONG Tenglong，ZHOU Hongwei，WANG Lujun，et al. Coal permeability model for gas movement under the three-dimensional stress[J]. Journal of China Coal Society，2018，43(7)：1930–1937.

[27] CHEN Dong，PAN Zhejun，SHI J Q，et al. A novel approach for modelling coal permeability during transition from elastic to post-failure state using a modified logistic growth function[J]. International Journal of Coal Geology，2016，163：132–139.

[28] ZHU Wangcheng，WEI Chenhui. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model[J]. Environmental Earth Sciences，2011，62(1)：43–54.

[29] 李松林，李忠城，王利娜，等. 寿阳区块高阶煤煤体结构及破裂压力测井解释方法[J]. 煤田地质与勘探，2020，48(6)：146–154.

LI Songlin，LI Zhongcheng，WANG Lina，et al. High rank coal structure and log interpretation method of fracture pressure in Shouyang block[J]. Coal Geology & Exploration，2020，48(6)：146–154.

[30] LI Bobo，REN Chonghong，WANG Zhihe，et al. Experimental study on damage and the permeability evolution process of methane-containing coal under different temperature conditions[J]. Journal of Petroleum Science & Engineering，2020，184：106509.

[31] 李波波，杨康，袁梅，等. 不同温度下孔隙压力对煤岩渗流特性的影响机制[J]. 地球科学，2017，42(8)：1403–1412.

LI Bobo，YANG Kang，YUAN Mei，et al. Effect of pore pressure on seepage characteristics of coal and rock at different temperatures[J]. Earth Science，2017，42(8)：1403–1412.

[32] 许江，周婷，李波波，等. 三轴应力条件下煤层气储层渗流滞后效应试验研究[J]. 岩石力学与工程学报，2012，31(9)：1854–1861.

XU Jiang，ZHOU Ting，LI Bobo，et al. Experimental research on seepage lagging effects of coalbed methane reservoir ender condition of triaxial stress[J]. Chinese Journal of Rock Mechanics and Engineering，2012，31(9)：1854–1861.

[33] ZHAO Wei，WANG Kai，LIU Shimin，et al. Asynchronous difference in dynamic characteristics of adsorption swelling and mechanical compression of coal：Modeling and experiments[J]. International Journal of Rock Mechanics and Mining Sciences，2020，135：104498.

[34] 梁冰，章梦涛，潘一山，等. 瓦斯对煤的力学性质及力学响应影响的试验研究[J]. 岩土工程学报，1995，17(5)：12–18.

LIANG Bing，ZHANG Mengtao，PAN Yishan，et al. The experimental research on the effect of gas on mechanical properties and mechanical response of coal[J]. Chinese Journal of Geotechnical Engineering，1995，17(5)：12–18.

[35] 许江，李树春，刘延保，等. 基于Drucker–Prager准则的岩石损伤本构模型[J]. 西南交通大学学报，2007，42(3)：278–282.

XU Jiang，LI Shuchun，LIU Yanbao，et al. Damage constitutive model of rock based on Drucker-Prager criterion[J]. Journal of Southwest Jiaotong University，2007，42(3)：278–282.

[36] 何满潮，谢和平，彭苏萍，等. 深部开采岩体力学研究[J]. 岩石力学与工程学报，2005，24(16)：2803–2813.

HE Manchao，XIE Heping，PENG Suping，et al. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(16)：2803–2813.

[37] 郑颖人. 岩土塑性力学的新进展–广义塑性力学[J]. 岩土工程学报，2003，25(1)：1–10.

ZHENG Yingren. New development of geotechnical plastic mechanics-generalized plastic mechanics[J]. Chinese Journal of Geotechnical Engineering，2003，25(1)：1–10.

Plastic deformation-based constitutive relation of coal damage and permeability model

WU Xuehai1, LI Bobo1,2,3, WANG Xin4, GAO Zheng1, LIJianhua1, XU Jiang5

(1. College of Mining, Guizhou University, Guiyang 550025, China; 2. National Joint Engineering Laboratory for the Utilization of Dominant Mineral Resources in Karst Area, Guizhou University, Guiyang 550025, China; 3. Guizhou Key Laboratory of Comprehensive Utilization of Non-metallic Mineral Resources, Guiyang 550025, China; 4. Bijie Zhongcheng Energy Co., Ltd., Bijie 552109, China; 5. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China)

Coal and gas outburst induced by mining disturbance is one of the main gas dynamic disasters in coal mine production. In order to systematically explore the evolution characteristics of coal damage and the law of gas seepage under mining disturbance, the whole stress strain–seepage experiment under different gas pressures was carried out. The generalized Hooke’s law was modified by considering the effects of gas adsorption and thermal expansion, the plastic deformation-based constitutive relation of coal damage was established, and the piecewise permeability model considering the damage was further constructed. The results shown that the coal permeability can be divided into two stages: before and after the peak, taking the sudden change point of permeability as the boundary. The permeability decreases exponentially before the peak and increases sharply after the peak, and the peak compressive strength and elastic modulus decrease with the increase of gas pressure. The evolution law of axial plastic strain and damage of coal has good consistency, and both of them show a trend of little change before the peak and rapid increase after the peak. The damage model and permeability model were verified by using the experiment data under different gas pressures and 50℃, and the theoretical curves were in good agreement with the experiment data, which shows that the new model can better reflect the damage evolution law and gas seepage characteristics in the process of coal damage and the instability under different conditions.

coal and gas outburst; plastic deformation; damage; permeability; mining disturbance

语音讲解

P618.11

1001-1986(2021)06-0131-11

2021-06-17；

2021-08-19

国家自然科学基金项目(52064007，51804085)；贵州省省级科技计划项目(黔科合基础-ZK〔2021〕重点052)

吴学海，1997年生，男，贵州织金人，硕士研究生，从事岩石力学、矿山安全与灾害防治方面的研究工作. E-mail：568138241@qq.com.

李波波，1985年生，男，贵州修文人，博士，教授，博士生导师，从事岩石力学与工程方面的教学与研究工作. E-mail：bbli@gzu.edu.cn.

吴学海，李波波，王新，等. 基于塑性变形的煤体损伤本构关系及渗透率模型研究[J]. 煤田地质与勘探，2021，49(6)：131–141. doi: 10.3969/j.issn.1001-1986.2021.06.016

WU Xuehai，LI Bobo，WANG Xin，et al. Plastic deformation-based constitutive relation of coal damage and permeability model[J]. Coal Geology & Exploration，2021，49(6)：131–141. doi: 10.3969/j.issn.1001-1986.2021.06.016