基于AR-PLS的FCM聚类在线性能评价

高新域，陶文华，王玉英

（1.辽宁石油化工大学 信息与控制工程学院，辽宁抚顺 113001；2.中国石油辽阳石化分公司，辽宁辽阳 111003）

工业过程工艺复杂、流程多，受装置老化、人员操作失当、生产环境改变等因素的影响，工业过程性能会偏离最佳工作状态，可能导致经济性能变差甚至生产事故[1]。因此，针对工业过程设计一种在线性能评价模型是很有意义的。

近年来性能评价方法得到了快速发展，大致分为基于解析模型的方法、基于知识的方法及基于数据驱动的方法三种[2]。其中，主成分分析法、独立主元分析法及偏最小二乘法是基于数据驱动的方法中应用较广泛的算法。主成分分析法可用于工业生产过程建模与故障检测[3-4]，其基本思路是将高维原始数据转换为低维的特征元素进行建模。但是，主成分分析法只关注过程变量组成的数据空间，没有将与工业生产质量相关的变量纳入考虑范围。梁北辰等[5]采用偏最小二乘法提取与工业生产质量相关的信息。传统偏最小二乘法使用非线性迭代算法，因此运算过程比较复杂[6]。S.Yin等[7]使用自回归思想对传统偏最小二乘法改进，建立由回归系数形成的投影空间，依据与质量变量的相关性，对样本数据空间进行分解。改进后的算法降低了运算的复杂性，并且避免了不必要的分解[8]。在数据分析领域，聚类分析算法同样有着广泛的研究与应用[9]，如K均值聚类算法、模糊C均值(Fuzzy C-Means，FCM)聚类算法[10]。K均值聚类算法将K类向量作为聚类中心，依据与聚类中心的距离进行聚类，不断优化样本分类，并计算新的聚类中心，在数据量过多的情况下会耗费大量计算时间。FCM聚类算法是K均值聚类算法的推广形式，数据属于某类由隶属度函数决定，各样本点不直接隶属于单个聚类中心，基本依据是“类内加权误差最小化”原则。该算法对于满足正态分布的数据聚类效果较好，且设计简单，可应用于多个领域[11]。本文采用自回归潜结构投影(Autoregressive Projection to Latent Structures,ARPLS)算法建立工业过程预测模型，通过FCM聚类算法对离线数据划分性能等级，得到各性能等级对应的隶属度函数，使用隶属度函数计算预测模型在线得到质量变量数据的隶属度，再依据隶属度判断性能等级，实现工业过程的在线性能评价。

1 自回归潜结构投影算法

自回归潜结构投影算法通过建立回归系数矩阵形成投影空间[8]，按照与输出变量的关联程度对输入变量的样本数据空间进行正交分解[12]。与传统偏最小二乘法相比，该方法能够简化数据建模过程。

在工业生产过程中，可以通过各类传感器及相关敏感元件获得采样数据，并转化为由n个指标及m个样本组成的输入变量矩阵X∈Rm×n，以及由m个样本及l个输出变量组成的输出变量矩阵Y∈Rm×l。输出变量矩阵Y代表工业过程性能的潜在变量，与工业生产过程中的输入变量相关。因此，在对工业生产过程进行建模时使用自回归潜结构投影算法对过程变量中的隐藏信息进行提取，将其映射到与潜变量Y相关的子空间中，并在此数据空间中建立工业生产过程离线模型。该算法将输入变量及输出变量分解为：

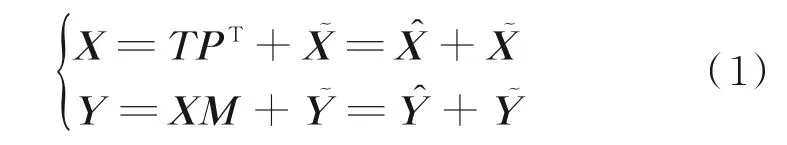
式中，T为得分矩阵；与为输入变量矩阵X的正交分解，其中，能对输出变量矩阵Y进行预测，而无法预测Y；为能够被过程变量X解释的子空间；为不可被输入变量X解释的子空间，满足cov(,X)=0；M为输入变量与输出变量间的回归系数矩阵。

式中，(XTX)†为(XTX)的伪逆矩阵。

当得到新的输入数据XNEW时，使用新的输出变量表示为：

自回归潜结构投影分解中的能够充分体现输出潜变量中输入变量的变化，排除无关信息对性能分析的干扰，提高运算效率。相较于传统偏最小二乘法，本数据空间分解方法更加适用于工业生产过程的离线建模。

2 FCM聚类算法

聚类分析是依据一定标准对事物间的接近程度进行判别，将彼此接近的事物进行归类的算法。FCM聚类算法通过求解有约束的最优化问题，进而获得样本数据的模糊划分以及分类结果[13]。该算法能够克服硬分类算法将数据归属“一刀切”的劣势，在一定程度上弥补不确定因素对数据聚类造成的影响[14]。

令X={x1,x2,…,xn}为由n个指标构成的输入变量矩阵，V={v1,v2,…,vc}为c个类别中各类别的聚类中心，U={uij}为隶属度矩阵,uij为xj对于第i类的隶属度，dij=‖ ‖xj-vi为样本点xj到聚类中心vi的欧氏距离。

FCM聚类算法的关键点是寻找合适的隶属度与聚类中心，使类内耗费函数的方差与迭代误差达到最小。耗费函数的值为数据到聚类中心二范数测度的加权累积和。

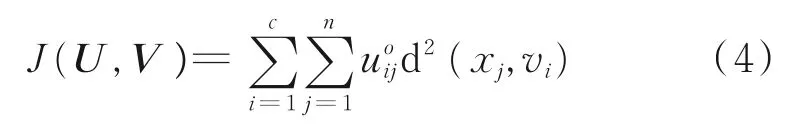
式中，J(U,V)为类别内的数据到聚类中心的加权距离平方和，J(U,V)值反映数据类别的一致性，其值越小表明聚类效果越好；m为隶属度加权指数，该参数决定聚类结果的模糊程度，o∈[1,+∞)，其值越大表明聚类结果越模糊，一般取o=2。式（4）需要满足如下的约束条件：

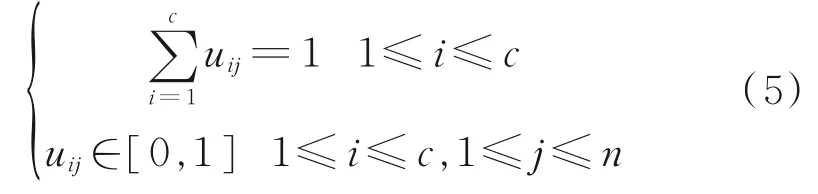
为使J(U,V)达到最小，该带约束条件的极值问题可通过拉格朗日乘子进行求解，迭代算法的计算过程为：

（1）算法初始化：设定聚类类别数目，迭代终止条件ε，用随机数初始化隶属度矩阵U(0)，令迭代次数k=0。

（2）计算聚类中心：

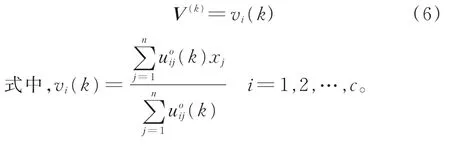
（3）计算隶属度矩阵：

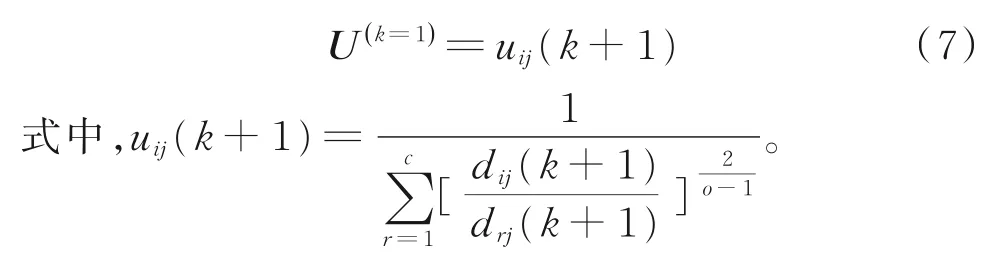
3 在线性能评价方法

首先使用自回归潜结构投影算法，基于离线数据建立工业生产过程预测模型，然后通过FCM聚类分析算法计算建模数据中输出变量数据对于各性能等级的隶属度，并得到各变量对于每个性能等级的隶属度函数。对在线数据进行性能评价时，由于生产过程存在滞后，先利用预测模型及输入变量数据对输出变量进行预测，再用隶属度函数计算各输出变量预测值对于各性能等级的隶属度，最终通过模糊算子得到该时刻所属的性能等级。

3.1 性能评价模型的建立

使用离线建模数据，通过自回归潜结构投影算法建立预测模型，并且用FCM聚类算法得出各输出变量对于各性能等级的隶属度函数。详细过程为：

（1）由于工业生产存在滞后，获得的单个样本不能表征整体工业生产过程的性能状态[12]，因此本文在数据预处理时使用窗口宽度为H的数据平均值作为基本的评价单元，并计算数据窗口内数据的平均值作为融合后的数据集E*={}进行性能评价[10]。数据融合过程为：

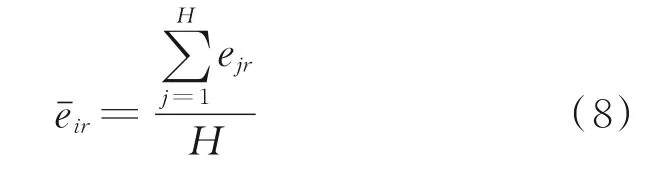
（2）通过式（8）处理后得到离线建模数据，依据评价要求划分为输入变量数据集xoff及输出变量数据集yoff两部分。

（3）根据评价需要，确定性能等级数目，使用FCM聚类算法，依据确定的性能等级数目，分别对各输出变量进行聚类，得到各输出变量对于各性能等级的隶属度。

（4）依据“最大隶属度”原则确定各指标对应的性能等级，并按照各等级分布特征确定各性能指标中各性能等级的隶属度函数fij(i=1,2,…,n;j=1,2,…,c)。

3.2 在线性能评价的过程

使用预测模型对在线获得的输入变量数据预测输出变量，通过隶属度函数分别计算各输出指标数据对于各性能等级的隶属度，最终利用模糊算子计算得到综合评价结果。

（1）选取l时刻时间窗口宽度H内的数据，使用式（8）进行数据融合，得到用于在线评价的l时刻输入变量数据向量xon。

（2）使用式（3），通过预测模型系数矩阵得到由各输出变量预测值组成的输出向量yon。

（3）使用各指标的等级隶属度函数，计算输出向量yon中指标数据对于性能等级的隶属度，根据“最大隶属度”原则确定输出向量yon中输出指标数据所属的性能等级。

（4）利用模糊算子对输出指标所属的性能等级进行模糊合成，得到该时刻系统所处的性能等级。

4 仿真验证

为测试所提方法的有效性，选择对高炉生产过程有重要影响的高炉炉温性能评价过程进行测试。

4.1 仿真背景简介

高炉炼铁是以焦炭、含铁矿石等原材料在高炉内生产生铁的工业生产过程，在现代钢铁生产过程中有重要的作用。高炉的炉况波动主要受炉温影响，因此炉温控制对高炉炼铁极为重要。高炉炉温对铁水中硅元素还原率较为敏感，因此常使用铁水硅质量分数反映高炉炉温状况。高炉冶炼过程中影响铁水硅质量分数的因素有很多，本文选取风量、风温、风压、透气性、富氧量、喷煤量、进料速度、铁量差这几种主要变量进行建模分析。

4.2 性能评价模型的建立

本文选取包头钢铁(集团)有限责任公司No.6高炉的生产数据，对高炉冶炼过程的炉温进行建模分析。高炉冶炼出铁时间一般为2 h,即120 min，使用式（8）对采集的过程数据进行初步处理。选取其中78组数据进行建模，将指标变量的离线数据作为预测模型的输入变量xoff。把高炉铁水硅质量分数视为间接反映高炉炉温状况的指标变量，并将其离线数据作为预测模型的输出变量yoff。利用输入变量数据及输出变量数据，通过式（2）计算得到预测模型系数矩阵M*。

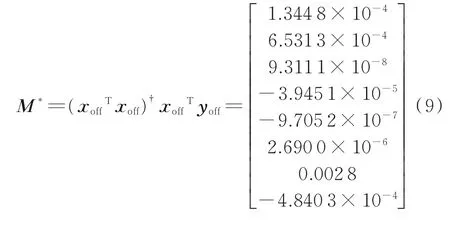
在线获得输入变量xon后，高炉炉温预测模型输出的预测值yon由式（3）计算获得。

利用能够反映高炉炉温状态的高炉铁水硅质量分数的离线数据，使用FCM聚类算法进行分析，得到高炉炉温各性能状态隶属度函数。高炉炉温状态可大致分为偏高、偏低及正常三种，因此本文将高炉铁水硅质量分数数据划分为三种类别。FCM聚类算法得到的各类别隶属度分布曲线如图1所示。

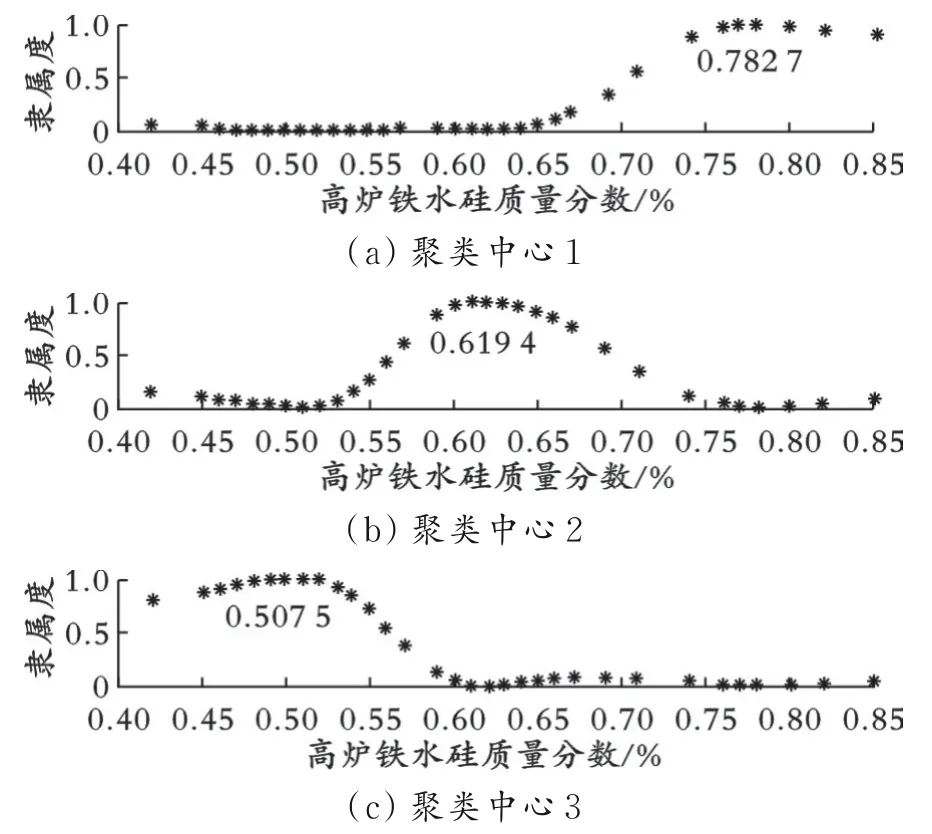
图1 基于FCM聚类算法的各类别隶属度分布

从图1可以看出，高炉铁水硅质量分数数据分布近似满足高斯分布，因此使用式(11)高斯分布函数作为隶属度函数。

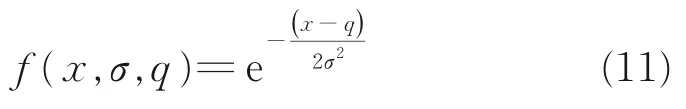
式中，x为输入变量；σ决定高斯分布的胖瘦程度，σ=0.026；q为高斯分布的中心。

高炉炉温各性能等级的隶属度函数参数见表1。

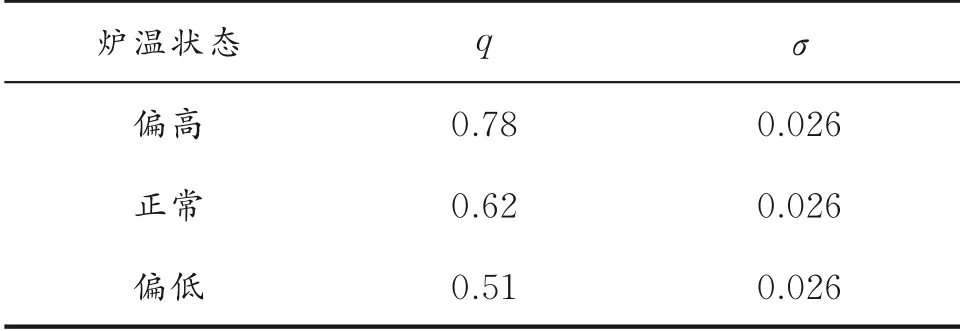
表1 高炉炉温各性能等级的隶属度函数参数

基于上述参数的高炉炉温各性能等级的隶属度函数曲线如图2所示。

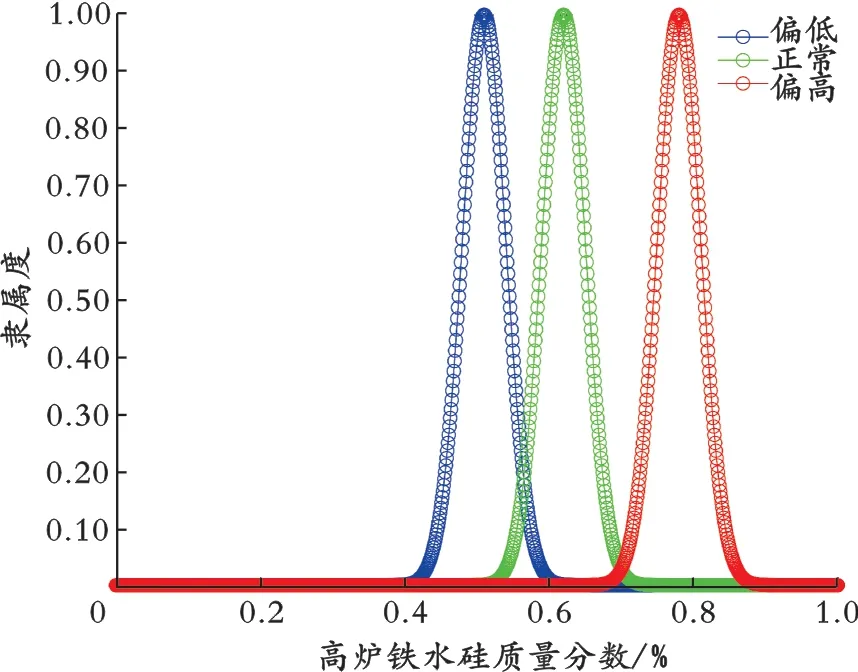
图2 高炉炉温各性能等级的隶属度函数曲线

使用隶属度函数计算，能间接反映高炉炉温状态的高炉铁水硅质量分数对于各性能等级的隶属度，判断高炉炉温状态。与FCM聚类算法得到的性能状态进行了对比，结果见表2。从表2可以看出，此隶属度函数能够准确反映样本数据所属类别。

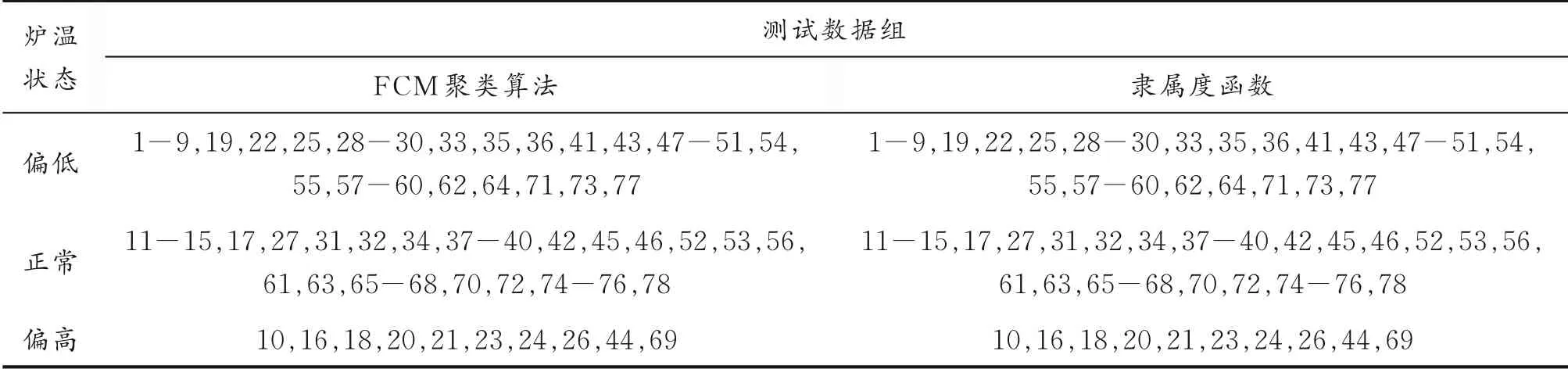
表2 FCM聚类算法分类结果与隶属度函数分类结果

4.3 在线性能评价方法验证

利用高炉的78组数据建立模型后，再通过另外37组数据对本文提出的在线性能评价方法进行验证。首先将AR-PLS算法得到的预测模型平均误差与偏最小二乘法得到的预测模型平均误差进行比较，然后将本文提出的在线性能评价方法的聚类结果与原始数据使用FCM聚类算法得到的聚类结果进行比较。

对进行验证的37组数据使用式（8）进行预处理，高炉炉温状态评价的主要变量划分为输入变量及输出变量两部分。将AR-PLS算法与偏最小二乘法的预测数据与原始数据进行对比，结果见图3，两种方法的平均误差见表3。

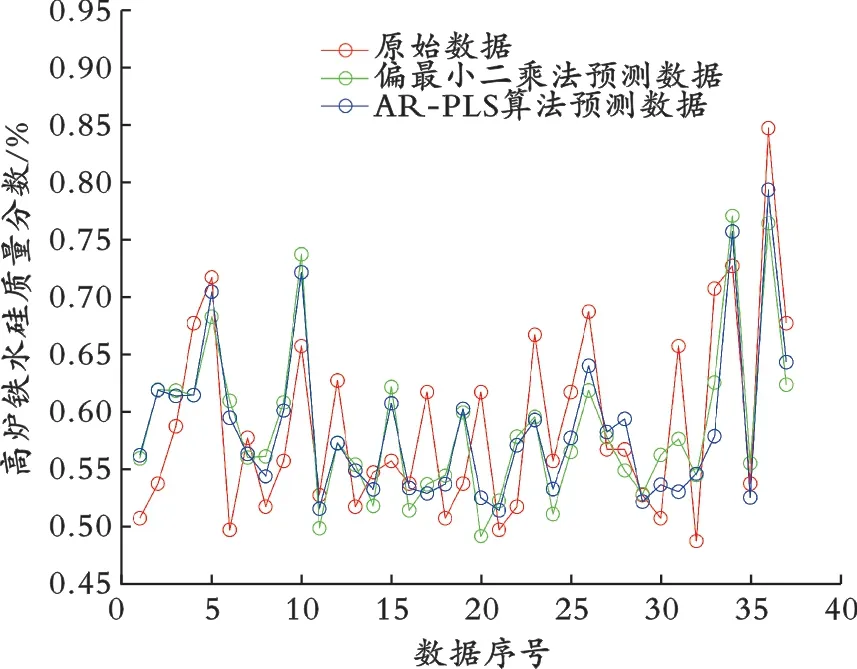
图3 铁水硅质量分数预测数据与原始数据

表3 AR-PLS算法、偏最小二乘法的平均误差

从图3及表3可以看出，AR-PLS算法在预测准确率上略优于传统的偏最小二乘法。

使用FCM聚类算法，通过高炉炉温各性能等级隶属度函数，分别计算原始数据和AR-PLS算法预测数据对于各性能等级的隶属度，并依据“最大隶属度”原则确定原始数据和AR-PLS算法预测数据对应的性能等级。评价结果见表4。

从表4可以看出，FCM聚类算法对AR-PLS算法预测数据的性能评价结果与对原始数据的性能评价结果相近。该预测模型在工业生产中能够较为准确地监测到异常情况的发生，进而提醒工程师采取相应措施。

表4 FCM聚类算法对原始数据与AR-PLS算法预测数据的性能评价结果

5 结论

针对传统偏最小二乘法存在复杂工业过程性能评价结果难以在线获得的问题，通过AR-PLS算法建立预测模型，并采用FCM聚类算法得到各性能等级隶属度函数，建立性能评价模型，对在线获取到的指标数据进行性能评价。以高炉炉温性能评价为背景对所提方法进行仿真分析，发现该方法使预测模型的建立过程更简洁，计算复杂度较低，能够较准确地反映工业过程变化，在非线性建模过程中也有着广泛应用。