基于ARIMA模型的股票价格实证分析

杨宇塬 张梅

摘 要：该文对大众公用（600635）股票开盘价建立ARIMA模型进行预测分析。使用Eviews9软件分析大众公用的股票开盘价，在对该数据分析前，需要先分析选取的股价时间序列数据的平稳性，若是不平稳序列，要把该数据平稳化处理后才能继续进行后续分析。实证分析结果表明，利用选取的ARIMA模型预测大众公用9天的开盘价，结果显示，预测的误差较小，说明该模型具有一定的参考价值和现实意义，ARIMA模型可以为投资者及相关投资机构提供股票投资决策参考。

关键词：ARIMA模型  股票开盘价  时间序列  股票预测

中图分类号：F832.51       文献标识码：A        文章编号：1672-3791（2021）10（b）-0000-00

Empirical Analysis of Stock Price Based on ARIMA Model

YANG Yuyuan  ZHANG Mei

（Guizhou University of Finance and Economics， Guiyang， Guizhou Province， 550025  China）

Abstract：The stock market is of great significance to a financial development. In the field of financial markets， stock data is a kind of time series data， which implies a series of operating laws. By analyzing these laws， we can make corresponding responses to the stocks in the market. Trend prediction can provide investors with decision-making support when investing in stocks. It is of great significance to investors and regional economic development. In the past， the basic analysis method of stocks was to analyze the trend of stock prices to predict， and most studies used methods such as combination forecasting and regression analysis to make long-term predictions of the trend of stocks and possible future prices. However， the predicted values of these methods have large errors. . The ARIMA model has been well developed in the analysis and application of time series. The model can predict stock price data more accurately. In addition to fitting a stationary time series， even non-stationary series， The ARIMA model also has a good fit.

Key  Words：ARIMA model; Stock opening price; Time series; Stock forecast

股票市場对一个金融发展有着十分重要的意义，在金融市场领域，股票数据作为一种时间序列数据，暗含着一系列的运行规律，通过分析这些规律，我们可以对市场的股票做出相应的趋势预测，能为投资者在进行股票投资时提供决策支持[1]，不管是对投资者还是地区经济发展都有着重要意义。以往股票的基本分析方法是分析股价走势来预测，而且大多数研究是使用组合预测、回归分析等方法对股票的走势及未来可能价格进行长期性的预测，但是这些方法的预测值存在较大误差[2]。ARIMA模型在对时间序列的分析应用上已经发展得比较完善，该模型能对股票价格数据进行比较准确的预测，除了能拟合平稳的时间序列，就算是非平稳的序列，ARIMA模型也有很好的拟合性[3]。

1 ARIMA模型的介绍

1.1 ARIMA模型

ARIMA模型（自回归移动平均模型）常用于拟合序列性质不会随时间变化的序列，即稳定时间序列[4]。ARIMA模型的提出就是为了对平稳时间序列进行建模、估计、检验及预测[5]。ARIMA（p， q）模型是两种模型的混合使用，AR模型是一种线性预测，对于一个平稳的时间序列y_t，认为y_t与之前的结果相关，可表示为p阶自回归模型[6]，记为AR（p），公式为：

y_t=β_0+β_1 y_（t-1）+β_2 y_（t-2）+…+β_p y_（t-p）+ε_t                        （1）

式中，y_t是一个平稳的时间序列，β_0是常数项，β_i （i=1，2，…，p）是AR模型的模型参数，表示AR模型的阶数，ε_t是误差。若当前结果y_t与之前扰动相关，则称为q阶移动平均模型，记为MA（q），公式为：

y_t=ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-…-θ_q ε_（t-q）                              （2）

式中，θ_i （i=1，2，…，p）是MA模型的模型参数，  q表示MA模型的阶数，ε_t为误差。ARIMA模型是最常用的拟合平稳时间序列的模型，y_t的取值不仅和 p期序列值有关，还与q期扰动项有关，公式为：

y_t=β_0+β_1 y_（t-1）+β_2 y_（t-2）+…+β_p y_（t-p）+ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-…-θ_q ε_（t-q）                                                            （3）

式中，β_i （i=1，2，…，p）和θ_i （i=1，2，…，p）是ARIMA模型的模型参数，{ε_t }是白噪声序列，p，q是非负整数[7]。而ARIMA中的d表示的是该时序数据需要经过几阶差分化才是平稳的。

2 股票收盘价实证分析及预测

该文数据来源于雅虎财经网大众公用燃气供应和生产公司的股票开盘价，选取其2019年1月2日至2021年9月13日的656组开盘价数据，利用Eviews9建立ARIMA模型对数据进行建模预测。

2.1 平稳性及纯随机性检验

将选取的大众公用的股票数据导入Eviews9软件，建模前通过时序图初步判断时间序列的平稳性，再对其进行ADF检验，进一步准确地确定是否为平稳时间序列[8]。通过观察时序图及进行ADF检验判断序列平稳性，对包含截距项和趋势项的ADF检验。从表1的结果可以看出，1%显著性水平下的临界值为-3.972 126，而ADF检验的统计值为-3.338 636。ADF检验值在1%显着性水平上大于临界值，没有拒绝有单位根的假设，认为时间序列是非平稳的。选择ADF测试截距项，无趋势;无趋势和截距。检验结果表明没有拒绝原假设，所以时间序列不平稳。

以上检验结果表明，在显著性水平0.05下，原假设成立，即原序列存在单位根，原始序列是非平稳序列。因此，有必要平稳化时间序列，我们通常以差分改变时间序列平稳性。

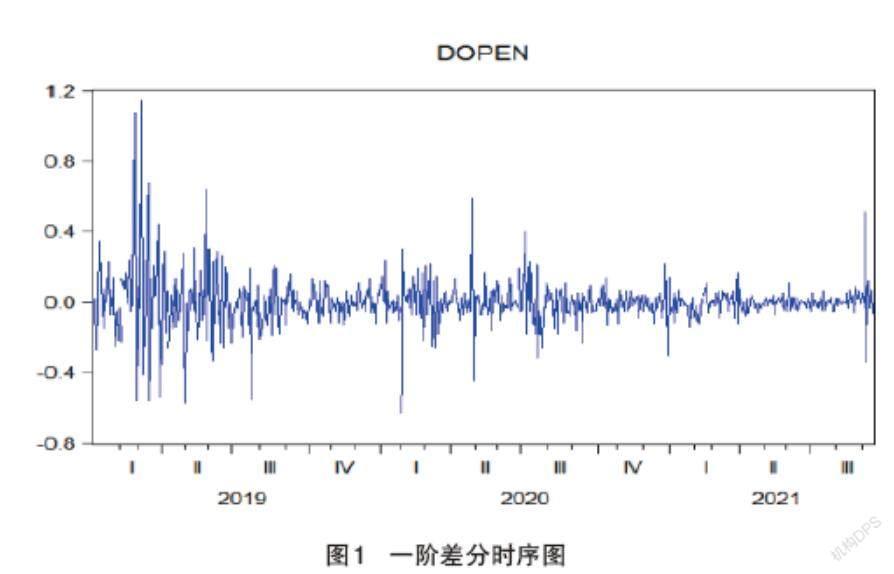
如图1所示，原始序列经过一阶差分后的序列{DOPEN}是平稳的，然后和上述检验原始序列步骤一样，对差分后的序列{DOPEN}进行ADF检验。从检验结果可以看出，1%显著性水平下的临界值结果显示-3.972 148，t值为-28.225 13。很明显，1%在显着性水平上远大于检验结果中的t值，原假设不成立，说明不存在單位根，序列{DOPEN}为平稳序列，ARIMA 模型中可确定d值为1。检验差分序列的纯随机性，如果是白噪音序列，则说明没有实用价值。检验结果显示Q统计量的P值检验结果：P≤0.05，所以{DOPEN}是非白噪声序列，具有相关性。

2.2 模型的建立

接下来根据一阶差分的相关图可知，ACF和PACF都在k=1，3，5处位于2倍标准差置信处边缘，由此尝试使用ARIMA模型进行拟合， p、q值可分别取1，3，5，建立ARIMA（1，1，1）、ARIMA（1，1，3）、ARIMA（1，1，5）、ARIMA（3，1，1）、ARIMA（3，1，3）、ARIMA（3，1，5）、 ARIMA（5，1，1）、 ARIMA（5，1，3）、ARIMA（5，1，5）9个模型。在Eviews中输入相应的模型p、q值之后，通过模型的AIC、SC、HQ准则和t统计量的显著性来确定合适的模型。由表2可知，ARIMA（1，1，5）的AIC和SC值最小，因此，选择ARIMA（1，1，5）建立模型。

通过上面的模型定阶及模型的确定，选择ARIMA（1，1，5）作为较优的拟合模型，去掉常数C后的模型，AIC值变得更小，这说明去掉常数C后的ARIMA（1，1，5）模型更加准确。因此，该模型对应的表达式为：

y_t=0.683440y_（t-1）+ε_t-0.792026ε_（t-1）+0.087327ε_（t-2）-0.137486ε_（t-3）+0.075591ε_（t-4）+0.096305ε_（t-5）

2.3 模型检验及应用

接下来对模型的残差序列进行白噪声检验，若不是白噪声序列，则说明模型的拟合效果需要进一步改进。对序列做了自相关图（ACF）和偏自相关图（PACF），从结果可以看出Q统计量均小于显着性水平0.05%的卡方分布临界值，相关系数接近0，在两条虚线内，即残差序列没有相关性，为白噪声序列，说明模型ARIMA（1，1，5）比较符合要求。接下来用该模型对大众公用股价进行预测。预测结果显示，预测效果还是比较好的。将预测结果与实际值进行比较，如表3所示，从表3中可以看出，预测值与真实值很接近，且预测的误差比都小于0.1，这说明预测的开盘价与实际值误差较小。

从预测结果分析可知，使用ARIMA模型对的股价进行短期预测是可行的，误差比较小，该模型能为股票投资提供一定的决策依据;但是，如果继续使用该模型进行长期的预测分析，可能会导致预测误差累计，预测就不会那么准确了。而且影响股价的因素还有很多，如政府政策宏观调控与一些社会突发事件等，这些外在因素都可能对ARIMA模型的预测结果准确性产生影响。

3 结语

该文对大众公用2019年1月2日至2021年9月13日的656组开盘价数据进行建模预测，对其中5天的开盘价进行估计。结果显示，大众公用的股票价格有上升的趋势，且误差较小，通过预测值与实际值的对比下得出结论，ARIMA模型在短期预测上能为股票决策提供一定的参考价值，若作为长期的预测，还存在较大误差。该文只是对大众公用的股票开盘价进行建模分析，该模型的建立受股票数据的影响较大，模型受所研究的样本数据的影响比较敏感，缺乏普遍性。该文通过对大众公用开盘价的实例分析，使用ARIMA模型对其开盘价进行建模，对短期股价数据进行估计，希望能为投资者的投资计划提供一定的决策参考。

参考文献

[1] 刘松，张帅.运用ARIMA模型对股价预测的实证研究[J].经济研究导刊，2021（25）：76-78.

[2] 黄莉霞.基于ARIMA模型的股价分析与预测——以中国平安为例[J].科技经济市场，2020（10）：62-63.

[3] 陈浩，兰燕鸿，何郁波.基于ARIMA模型的股票开盘价分析及预测[J].吉首大学学报：自然科学版，2020，41（5）：86-91.

[4] 王越敬.基于LSTM-ARIMA混合模型的股价相关系数预测模型研究[D].绵阳：西南科技大学，2020.

[5] 陈颖.基于时间序列分析方法的金融数据研究[D].大连：大连理工大学，2019.

[6] 张亚婕.基于ARIMA模型对股票和指数预测结果的简单比较分析[J].市场研究，2019（11）：23-26.

[7] 丁玮珂.基于ARMA模型预测股票价格的实证分析[J].广西质量监督导报，2019（5）：151-153.

[8] 吴玉霞，温欣.基于ARIMA模型的短期股票价格预测[J].统计与决策，2016（23）：83-86.