2021年新高考全国I卷数学19题错因解析及备考策略

>>>高 宏

2021年新高考全国Ⅰ卷数学19题是一道解三角形的问题，主要考查考生对正、余弦定理的掌握情况。第一问难度不大，大部分考生都可以得到相应的分值；但第二问区分度较大，大部分考生未能得到满分。本文先介绍该题的解法，再展示一些考生答题时出现的典型问题，最后分析原因并给出备考策略。

一、试题再现

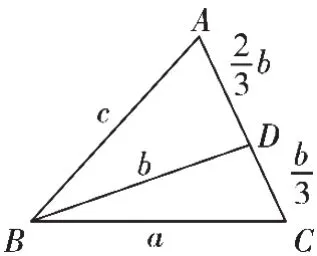
记△ABC 的内角 A，B，C 的对边分别为 a，b，c.已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.

（1）证明：BD=b；

（2）若 AD=2DC，求 cos∠ABC.

二、试题解析

三、典型问题

1.计算不细心失分

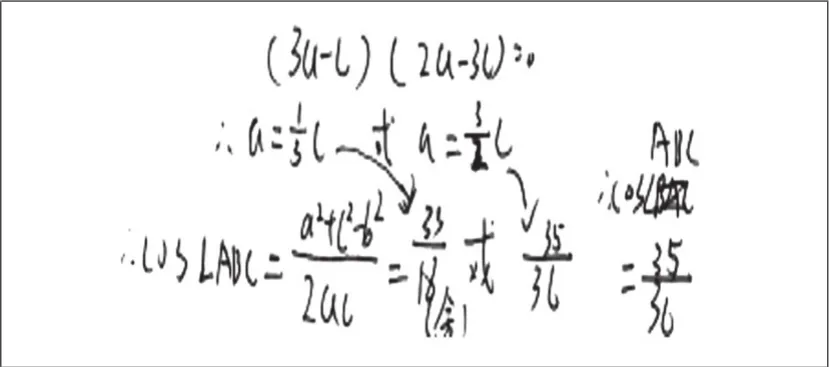
2.忽略余弦值的范围失分

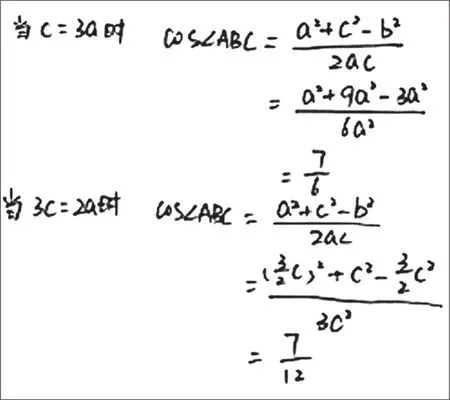
3.忽略已知条件，没有运用消元思想失分

4.双变量方程不会因式分解失分

5.没有找出三角形边长之间的关系进而求余弦而失分。

四、错因分析及备考策略

错因1：审题不认真，没有明确的计算方向。有用正弦定理计算的，算到一半放弃了；有用余弦定理去寻找边长a，b，c之间关系的，但是角的关系找不准，不能着眼于两个三角形中寻找等量关系；有的误认为∠ABD=∠CBD；有的用向量分析问题，但进一步求解没有方向。

备考策略：对三角函数基本公式的应用方法要了然于心，要条分缕析，善于归纳解题思路。比如已知三角形三条边时，首先想到用余弦定理解三角形；知道两边及其中一边所对角时，首先想到用正弦定理解三角形；做题时要多读几遍题目条件，关键的条件可以用笔圈出来。例如本题第二问，因为题目没有明确角与角之间的关系，而是给出了边长之间的关系，所以我们应锁定用余弦定理处理问题。

错因2：计算能力弱。例如在本题中，一是整理到了12a2-22ac+6c2=0，不约分；二是整理到了6a2-11b2+3c2=0，但忽略了已知条件b2=ac，解题受阻；三是对于6a2-11ac+3c2=0这个双变量的齐次式不会因式分解，或者是进行了正确的因式分解（2a-3c）（3a-c）=0，但在最后求解cos∠ABC时计算出错，或者没有对两个解进行取舍。

备考策略：总结运算规律，提升运算能力。比如，在解方程时要充分利用已知条件化多元为一元；遇到三角问题时化同角或同名；对代数式或方程能约分先约分，能因式分解要因式分解；对于二次方程不会因式分解的话也可以用求根公式进行运算；出现多解问题时要进行有理有据的取舍。