基于PSO‑SVR的飞行员工作负荷预测
2021-12-31张子文
杨 琪,黄 磊,陆 中,张子文,韩 冰
(1.南京航空航天大学民航学院,南京 211106;2.中国直升机设计研究所总体气动室,天津 300450)
飞行员工作负荷的大小与飞行安全紧密相关。同一时间段内的飞行事故,由飞行员差错导致的致命事故占比58%,机械故障占比17%[1]。飞行员出现差错的原因为执行飞行任务时工作负荷强度大,应激水平高。因此,飞行员执行飞行任务时的工作负荷已成为民用航空器适航审定中的一个重要指标。通过测量飞行员在执行任务时的工作负荷,可以分析驾驶舱的设计是否合理,是否满足适航规章的要求。对飞行员工作负荷进行预测分析是针对25.1302“飞行机组使用的安装系统和设备”、25.1523“最小飞行机组”等适航条款开展符合性验证的重要内容[2],是保证飞机设计满足安全性要求的重要手段。
飞行员工作负荷评价是对飞行员进行工作负荷预测的基础,针对飞行员工作负荷评价国内外已有学者做过一定研究。飞行员工作负荷评价方法主要分为基于生理指标参数的客观评价和基于量表的主观评价。针对工作负荷客观评价,Wilson等[3]在真实飞行中,采用10名飞行员在目视飞行仪表飞行状态下,发现视觉要求高的飞行场景下(工作负荷大),飞行员眨眼率下降;Veltman[4]验证了多种生理指标(心率、心率变异性、呼吸、血压和眨眼)在实际飞行中的可用性;Wilson等[3]在采用多生理指标研究飞行员脑力负荷时发现,脑电波(Electroencephalogram,EEG)数据中的α波和δ波随脑力负荷的变化而变化;针对工作负荷主观评价,常用方法主要有美国国家航空航天局任务负荷指数(National Aeronautics and Space Administration task load index,NASA-TLX)量表、库珀-哈珀(Cooper-Harper,CH)量表、主观工作负荷评价技术(Subjective workload assessment techniques,SWAT)量表等[5];辛甜等[6]采用NASA-TLX量表对飞行员工作负荷进行分析,结果表明NASA-TLX方法在细化工作负荷来源具有一定优越性;李琳君等[7]利用SWAT量表和贝德福德(Bedford)量表对直升机飞行员工作负荷进行评价。
建立飞行员生理指标与主观评价值之间的映射关系是对工作负荷进行准确评价的关键,人工神经网络广泛应用于该领域。刘树强建立了基于误差反向传播(Back propagation,BP)神经网络的机组工作量评估模型,并采用了遗传算法优化了BP模型的权值和阈值[8];李金波等以飞行员心理努力、任务主观难度、注视时间、注视次数、主任务正确率和主任务反应时6项指标为输入,以认知负荷的3个等级为输出,建立了基于BP神经络和自组织神经网络(Self-organization-map,SOM)的认知负荷综合评估模型[9]。Mazaeva等对30个EEG指标通过主成分降维后,采用自组织神经网络预测了信息加工要求不同的任务负荷的变化[10]。
从上述文献可以看出,目前对飞行员工作负荷评价的研究主要分为基于生理指标和基于主观量表两方面。而生理指标只能间接推断工作负荷大小,无法求得生理指标与工作负荷之间的函数关系,主观量表的评价结果受个体差异性的影响较大。在建立生理评价和主观评价两者之间关系的研究中,目前的研究主要集中在通过神经网络建立两者之间的关系,而在神经网络建模时,容易陷入局部最优,并且在网格训练中往往需要大量数据作为训练样本,并且在预测模型精度优化方面的研究较少。
针对以上所述各类方法的不足,本文提出了一种以粒子群算法优化的支持向量回归机(Particle swarm optimization-support vector regression,PSO-SVR)为核心的飞行员工作负荷评价模型,综合考虑飞行员的客观生理指标数据和主观评价数据,可对飞行员工作负荷进行准确评价及预测。通过PSO优化SVR的核函数参数和惩罚因子系数。将优化后的参数代入SVR模型中,以飞行员生理指标数据作为网络输入,主观评价数据作为网络输出,建立生理指标与主观评价值之间的非线性映射关系。通过主观评价实际值与预测值之间的对比,验证了所建模型的准确性。
本文首次将支持向量回归模型应用在飞行员工作负荷评估上,为工作负荷评估提出一种新方法。同时为了进一步提高工作负荷评估的精度,引入了粒子群优化算法。基于本文所提方法,在后续需要对飞行员进行工作负荷评价时,只需获取其客观生理数据,有效缩短工作负荷评估周期,同时无需飞行员进行主观评价,避免了由于飞行员主观评价带来的不确定性,提高工作负荷评价的准确性。
1 模拟飞行试验设计
基于某型运输类飞机模拟驾驶舱,构建模拟飞行试验。基于模拟飞行试验,采集飞行员生理指标数据和主观评价数据。
1.1 模拟飞行人员选取
选取民航学院45名男飞行员参与模拟飞行试验,年龄在20~25岁之间,视力正常、身心健康,飞行技术过硬。
1.2 模拟飞行阶段确定
参考某型运输类飞机飞行手册,对整机运行所有阶段进行模拟,各阶段划分如图1所示。

图1 模拟飞行阶段Fig.1 Simulated flight phase
各阶段描述如下。
滑出:飞机从停放位置移动到跑道;
起飞滑跑:释放刹车到离地之前;
起飞:离地35英尺;
起飞爬升:离地35~1500英尺;
爬升:离地1500~20000英尺;
巡航:飞机水平,离地高度大于20000英尺;
下降:离地大于20000英尺的任何高度到1500英尺;
等待:离地1500~20000英尺的任何高度;
进近:离地1500~100英尺;
着陆:离地100英尺到接触地面;
着陆滑跑:接触地面到速度达到滑行速度;
滑入:跑道至机场航站楼。
各阶段的持续时间分别为:滑出5min,起飞滑跑26.9 s,起飞5.5 s,起飞爬升1min,爬升6min,巡航45min,下降12min,等待根据实际情况,进近3.5 min,着陆10s,着陆滑跑20s,滑入5min。
1.3 模拟飞行状态选取
为了增加试验数据量,辅助SVR建模分析,通过改变飞机飞行状态,增加飞行员的工作负荷,设计正常模拟飞行状态和非正常模拟状态,非正常模拟状态包括主飞行显示器(Primary flight display,PFD)显示失效、单发失效、PFD显示和单发同时失效。
1.4 模拟飞行场景设计
模拟飞行场景由模拟飞行阶段和模拟飞行状态组合而成,设计如表1所示的模拟飞行场景。

表1 模拟飞行场景Table1 Simulated flight scene
1.5 试验数据采集
本飞行试验主要采集飞行员的生理指标数据以及主观评价数据,生理指标数据与主观评价数据均为多次测量后的平均值。
飞行员在进行信息处理(工作负荷发生变化)时,中枢神经系统会活动,与之相关的生理指标也会有所变化,因此可以通过测量生理指标的变化进而评价工作负荷[11]。生理指标评价方法中所使用的指标按照涉及的生理器官功能分为3大类:与心脏活动相关的生理指标、与眼睛活动相关的指标以及与大脑活动相关的生理指标。飞行员执行飞行任务需要对界面进行监控,而在视觉监控任务中,被试人员的瞳仁、眨眼率变化显著[12];刘树强通过相关性分析对飞行员心率、眨眼率、脑电功率与工作负荷主观评价值的相关性进行分析,结果表明所选生理指标数据与主观评价数据存在相关性[8];Kilseop等通过实验也证明了眼动、脑电功率和心率与工作负荷存在相关性,可以在一定程度上反映工作负荷大小[13]。因此,本文选取脑电功率、心率和眨眼率3项生理指标作为PSO-SVR模型的输入。脑电功率通过KT88-2400数字脑电仪进行采集分析;心率通过MD100A心电检测仪进行采集;眨眼率通过ASL504眼部跟踪仪进行采集。
目前常用的工作负荷主观评价法是CH量表法、SWAT量表法和NASA-TLX量表法。SWAT量表通过3个维度对工作负荷进行评估,NASA-TLX量表通过6个维度对工作负荷进行评估,相对于SWAT量表更为全面,评估值更准确。CH量表通过飞行员操纵飞机的主观感受,主要用于评估飞机的操纵性是否良好。因此在选用主观评估量表时采用NASA-TLX量表获取飞行员的工作负荷主观评估值[14]。
2 基于PSO‑SVR的工作负荷预测模型
粒子群算法通过优化SVR模型中核函数的两个重要参数:惩罚系数c和核函数参数g,从而提高算法的预测精度。本节包含构建基于SVR算法的飞行员生理指标数据与主观评价数据之间的非线性映射关系以及基于PSO的SVR模型参数优化两部分。
2.1 面向飞行员工作负荷预测的SVR模型
支持向量回归算法是基于统计学原理对样本数据进行预测,以建立样本输入与输出之间的非线性映射关系。本文采用非线性回归ε-SVR对飞行员工作负荷预测进行研究。
样 本 数 据 集{(x1,y1),(x2,y2),…,(x30,y30)},xi=(xi1,xi2,xi3),i=1~30,表 示 第i组 样 本 的 生理指标数据;xi1为第i组样本的脑电功率值;xi2为第i组样本的心率;xi3为第i组样本的眨眼率;yi为第i组样本的NASA-TLX评分值。
本文通过径向基核函数将样本数据集中的x映射到高维特征空间并进行线性回归,即有

式中g为核函数参数。
SVR算法结构如图2所示,回归函数为

图2 工作负荷预测的SVR算法结构图Fig.2 SVR algorithm structure diagram for workload prediction

为求c和b,引入损失函数有
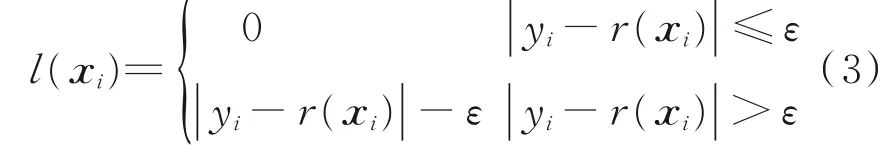
式中ε为不敏感系数,本文取值为0.01 。
所有样本点与回归函数r(x)之间距离都小于ε,结合结构分险最小(Structure risk minimization,SRM)准则,回归问题等价于二次凸优化问题,即

式中ξi、为松弛因子。
2.2 基于粒子群算法的SVR参数优化
粒子群优化算法是一种启发式优化算法,通过一组候选解(粒子)借助速度和位置更新公式在解空间内移动以解决优化问题。粒子的移动由自身经验和最优个体的经验进行调整,最终找到最佳位置[15]。
目前对SVR参数进行优化的方法主要有试凑法、网格搜索法和随机算法等。试凑法依赖于分析人员的经验,主观性较强;网格搜索法需要遍历网格内的所有参数点,操作复杂;随机算法中使用较多的是遗传算法,遗传算法在处理高维样本问题时,算法的收敛速度、精度有一定的限制。粒子群算法相对于其他算法而言参数设置较少、收敛速度较快且全局搜索能力较强,且模型简单易于实现,通用性较强[16]。因此,本文采取粒子群算法对SVR参数进行全局优化搜索。
本文中粒子的位置代表待优化参数c和g的值,粒子的速度代表c和g的变化率。设种群中粒子总数为n,第k代种群中各粒子的位置可以表示为

第k代群中各粒子的速度可以表示为

对惩罚系数c和核函数参数g进行优化,其流程如图3所示。

图3 基于PSO的SVR参数优化流程Fig.3 SVR parameter optimization process based on PSO
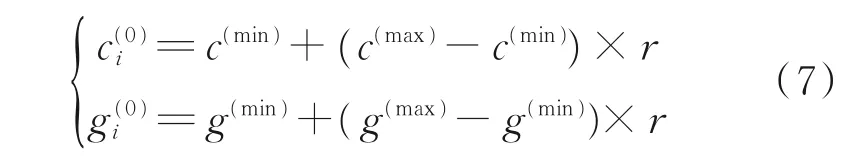
(1)初始化参数c和g的值及其变化率惩罚系数c和核函数参数g初始化为式中:c(max)、c(min)、g(max)、g(min)分别为参数c和g的最大值和最小值,r为(0,1)之间的随机数,i为粒子序号。
惩罚系数c和核函数参数g变化率为

(2)计算参数c和g对应的初始适应度值
选用K折交叉验证法样本数据集yi的均方误差(Mean square error,MSE)作为适应度函数有
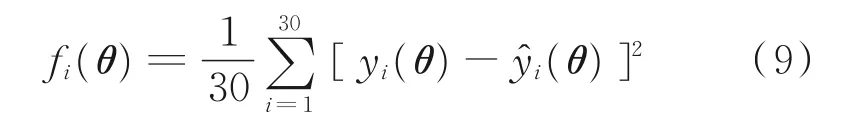
式中:yi(θ)为第i位飞行员的NASA-TLX评分值;ŷi(θ)为第i位飞行员的NASA-TLX预测值。
(3)初始化每一组c和g的最优值、全局最优c和g的值
将c和g初始最优值记为

c和g全局最优初始值g通过寻找f(θ(0))中最小值确定。
(4)更新参数c和g的变化率及其值
第k代种群中c和g的变化率更新为

式中:r为(0,1)之间的随机数;wk为第k代种群中变化率的惯性权重,即[17]

式中:K为最大迭代次数;k为当前迭代次数。
为了防止变化率超出范围,对更新后的变化率进行限制有
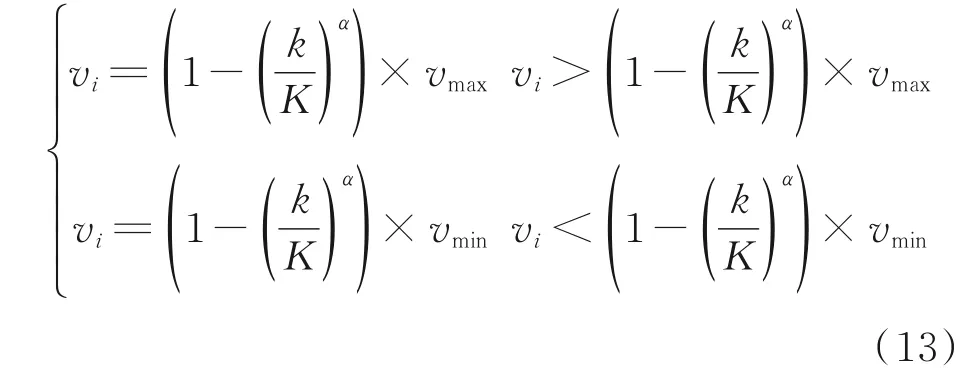
式中vmax、vmin为参数c或g变化率的最值。
动态学习因子C1、C2[18]

式中r1、r2、r3、r4为常数[19]。
第k代种群中参数c和g的值更新为

超出范围的参数处理如下
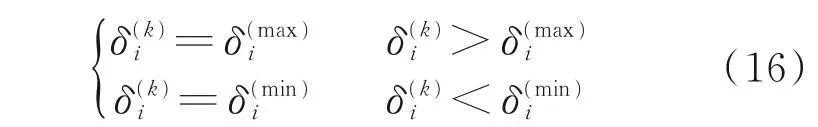
根据每组最优c和g的适应值更新全局最优c和g的值为

(6)判断是否满足终止条件
当迭代次数达到指定值时,或者适应度函数值收敛于指定值时停止迭代,否则返回步骤(4)。
2.3 PSO‑SVR预测模型误差分析
根据预测结果相对实际结果的误差百分比对预测结果进行误差分析。相对误差百分比

式中:a0(m)表示第m组样本数据的预测值;t0(m)表示第m组样本数据的实际值。
平均相对误差百分比

式中m=1,2,…,M表示第m个样本数据。
3 实例分析
以某型号民用飞机为例,对该型飞机飞行员的工作负荷进行预测分析。基于本文设计的模拟飞行试验,获取飞行员的脑电功率、心率变化量、眨眼率以及NASA-TLX量表评分值,其中脑电功率为绝对功率值,心率变化量和眨眼率以“次/min”为单位,脑电功率和NASA-TLX评分值量纲为一。场景1~4分别获取45组试验数据(见附录1~4)。取每个场景前30组作为训练样本,后15组作为预测样本。

为了比较优化后的预测精度,采用默认参数的SVR预测模型和本文建立的PSO-SVR模型分别进行训练,NASA-TLX预测结果如表2所示。将SVR模型与PSO-SVR模型的NASA-TLX预测值与实际值之间进行对比如图4所示。

图4 SVR/PSO-SVR模型的NASA-TLX预测值与实际值对比Fig.4 Comparison of NASA-TLX prediction results of SVR/PSO-SVR model with actual results
对表2中各样本进行误差分析,由式(19)得SVR/PSO-SVR预测模型的样本相对误差如表3所示。

表2 SVR模型与PSO‑SVR模型NASA‑TLX预测结果Table2 NASA‑TLX prediction results of SVR model and PSO‑SVR model
根据表3中SVR/PSO-SVR误差,由式(20)可得场景1~4的SVR预测模型样本平均相对误差分别为13.8 %、14.8 %、12.2 %和9.9 %,PSO-SVR预测模型样本平均相对误差分别为6.3 %、5.3 %、5.2 %和4.1 %,将表3中SVR误差与PSO-SVR误差以折线图的形式进行对比如图5所示。

表3 SVR/PSO‑SVR预测模型相对误差Table3 Relative error of SVR/PSO‑SVR prediction models %
由图5可知,除个别样本出现优化后误差增大的情况,绝大多数样本经过PSO优化后预测误差都减小,与SVR相比,PSO-SVR的预测精度更高,表明利用粒子群算法对SVR参数进行优化的方法非常有效。

图5 SVR/PSO-SVR模型相对误差对比Fig.5 Relative error comparison of SVR/PSO-SVR model
为了验证上述模型的有效性与正确性,设置区别于场景1~4的4组不同的飞行场景记为场景5~8,获取飞行员的工作负荷主观评价值与客观生理评价数据。利用上述评估模型预测出新设置的4组不同飞行场景下飞行员工作负荷主观评价值,并与实际获取到的值进行对比,分析其误差是否在可接受的范围之内,4组场景的误差对比结果的如图6所示。从图6的误差对比可以看出,针对不同场景优化后的预测模型能够将误差控制在10%以内。

图6 新增场景下的SVR/PSO-SVR模型相对误差Fig.6 Relative error of SVR/PSO-SVR models in new scenes
4 结 论
本文对飞行员工作负荷评价方法进行了研究,提出了基于PSO-SVR的飞行员工作负荷预测方法,通过对比验证说明了本文方法的合理性。本文将支持向量回归模型应用在飞行员工作负荷预测上,为飞行员工作负荷评估提供了一种新方法。为了进一步提高工作负荷预测的精度,本文提出了基于PSO-SVR的飞行员工作负荷预测模型,对SVR模型进行改进,通过与本文所提的SVR模型的对比以及与基于BP神经网络的机组工作量评估模型的对比[8],PSO-SVR工作负荷预测模型具有更高的预测精度,表明本文所提方法是有效的。
实例分析中多组场景的预测结果表明,本文所提模型能够将飞行员工作负荷预测误差控制在可接受的范围之内。表明本文所提的PSO-SVR工作负荷预测方法对不同飞行场景的适用性。利用本文所提方法,在进行飞行员工作负荷适航符合性验证时,只需测量飞行员生理指标数据而不用多次对飞行员进行工作负荷主观评价,既能够避免飞行员的主观不确定性,提高符合性验证的准确性,同时提高了符合性验证的效率。
本文所提PSO-SVR模型在预测精度上的确要优于SVR模型,但是从不同场景的预测精度上看,仍然存在一定误差,原因在于建模所用数据存在的局限性,数据量和建模所用的工作负荷主观评估值的准确性是主要原因,后续需要通过
附录
场景1~4试验样本数据,如附表1~4所示。增加数据量以及增加建模所用输出数据(工作负荷主观评估值)的准确性提高模型的预测精度。
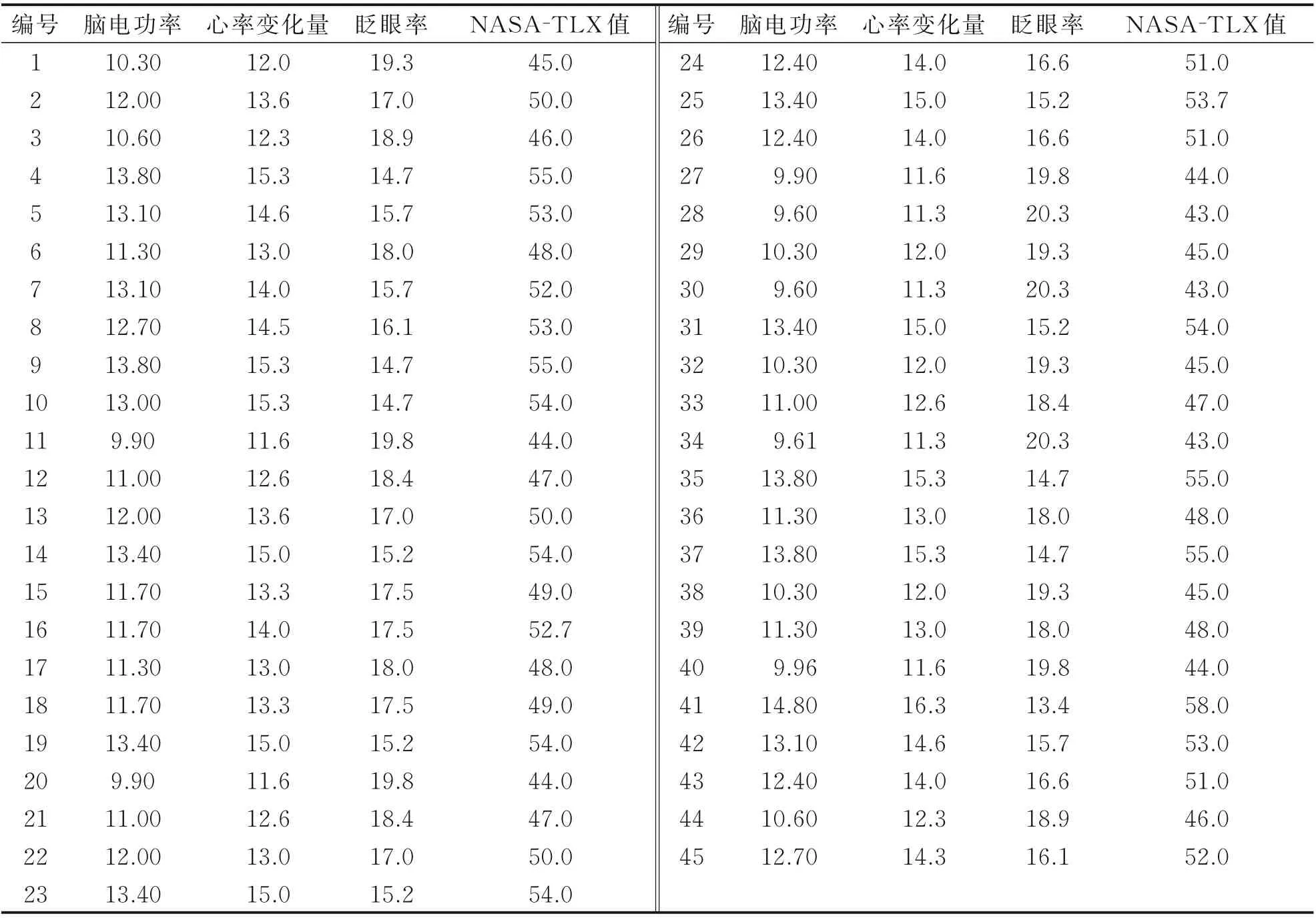
附表1 场景1样本数据Annexed table1Sample data for scene1
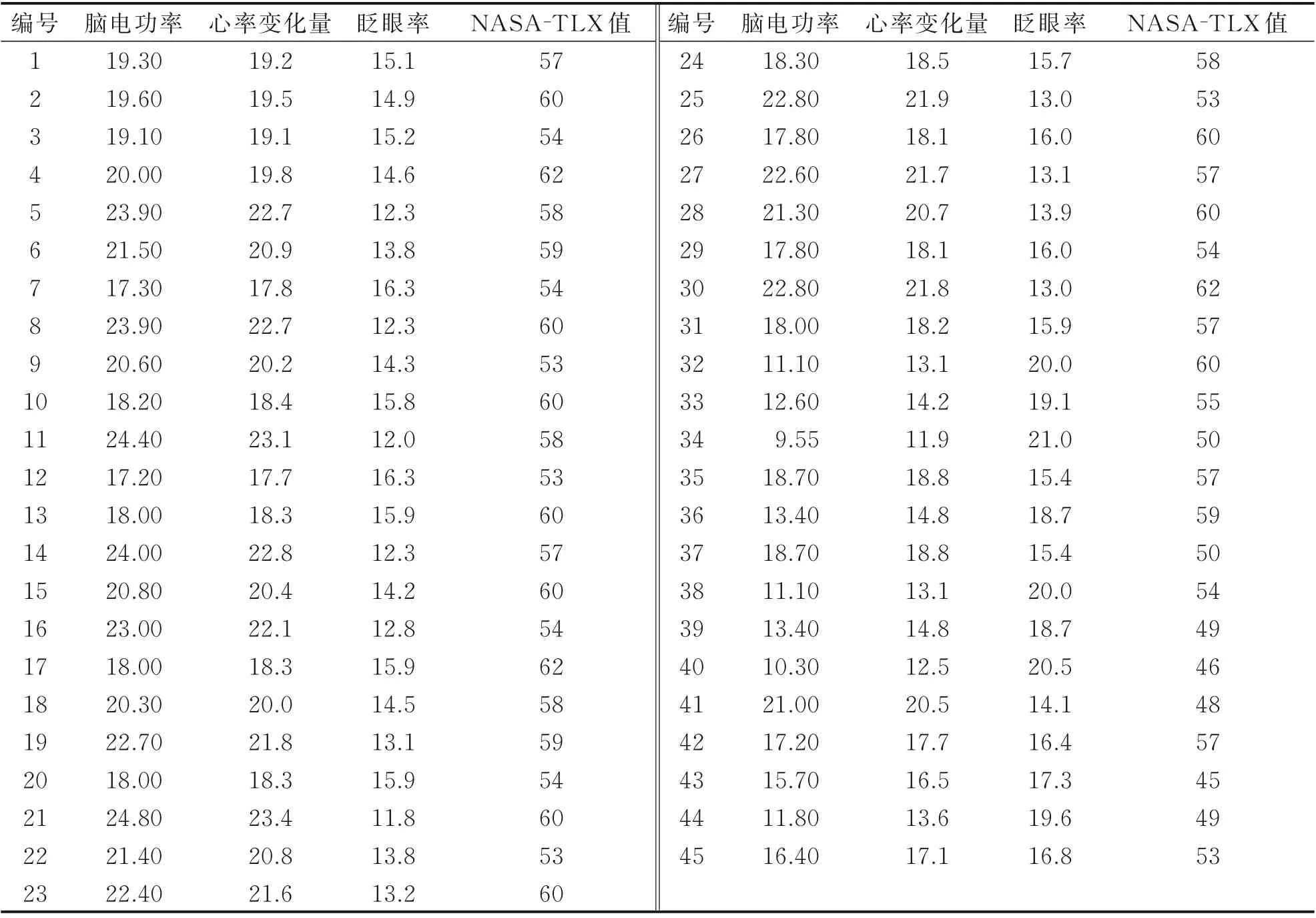
附表2 场景2样本数据Annexed table2Sample data for scene2

附表3 场景3样本数据Annexed table3Sample data for scene3

附表4 场景4样本数据Annexed table4Sample data for scene4
