基于模糊推理的无人战斗机视距空战机动决策
2021-12-31杨任农梁晓龙张佳强
吴 傲,杨任农,梁晓龙,张佳强
(1.空军工程大学航空集群技术与作战运用实验室,西安 710051;2.陕西省电子信息系统综合集成重点实验室,西安 710051;3.空军工程大学空管领航学院,西安 710051)
自主决策能力是无人战斗机(Unmanned combat aerial vehicle,UCAV)发挥作战效能的关键[1-3]。自主空战是UCAV参与空战的最终形式,而机动决策对于正在到来的无人空战时代则是必不可少的研究内容[4]。
空战机动决策是指:基于数学优化、人工智能等方法,模拟各种空战态势下飞行员的决策,自动生成对飞行器控制指令的决策过程[5]。文献[6]将目前的空战机动决策分为基于对策方法和基于人工智能方法。基于对策的方法主要有矩阵对策[4,7-8]、影 响 图[9-11]等。矩 阵 对 策 法 往 往 以 博 弈论[7]为基础,能充分考虑敌我双方的对抗关系,但是纳什均衡的求解较为烦琐,并且在决策过程中难以加入对敌方意图的推断;影响图[9-11]能很好地反映飞行员决策的过程,能引入环境的不确定性和飞行员的决策偏好,但其建模复杂,求解计算量大,难以满足决策的实时性要求。基于人工智能的方法主要有专家系统法[12]、遗传算法[8]以及强化学习方法等。专家系统法主要依靠人为设定机动动作库,决策的结果是离散的机动动作序列,计算量小,适合空战实时决策,但也往往受到专家经验的限制,同时文献[13-14]的机动动作库均采用了最大过载的机动动作,并不能很好地反映真实的飞行过程;遗传算法[8]等智能算法可以将UCAV的控制量生成连续的控制序列,极大地提升了UCAV的可控性,但是连续控制量的求解规模较大;以神经网络[15-17]为基础的强化学习算法是目前解决UCAV机动决策的热点,但是对算法的训练要求较高。
上述方法在求解简单的机动决策方面具有一定的优势,但当UAV机动方式较为复杂时容易出现维数灾难、依赖人的主观性以及规则漏洞等现实问题。为克服上述方法的不足,潘耀宗等[18]将深度强化学习(Deep reinforcement learning)引入UAV自主空战机动决策研究中,提出了一种基于深度Q网络(Deep Q-network)的双网络智能决策方法,有效解决了UAV向己方攻击区自主机动的决策问题。冯志峰等[19]为了克服无人机在通信中断情形下无法有效执行作战任务的问题,提出一种基于规则推理的UAV自主决策方法。该方法采用事实与作战规则对比匹配的方法,推理得到对应的决策策略。任天助等[20]通过模拟人的情感决策过程提出了一种基于情感智能的决策方法,并将该方法应用于求解无人机航路规划和威胁规避的自主决策问题。但该方法考虑的模型较为简单,在实际应用中还有待提高。另外,在进行Q学习的数据样本设计过于理想化,使得学习出来的经验不具有普适性。李维等[21]以构建规则库的形式,提出了一种基于知识库的自主决策方法。该方法借助贝叶斯网络模拟人态势的认知,借助规则进行决策,并利用实体的状态变迁来控制流程,从而实现无人机的自主决策。
空战机动决策的最终决策量往往为当前或未来一段时间内空战态势下最优的机动动作控制量,因此空战态势评估是UCAV机动决策的基础,在空战中将为UCAV的机动决策提供重要信息支撑。但是空战态势信息具有高度的抽象性、模糊性以及难解释性[22-23],因此合理的表达态势信息是关键。文献[24-25]利用贝叶斯推理的方法将空战态势划分为4种,基于态势评分结果给出了变权重的机动决策函数,但是在态势评估过程中却没有考虑高度和速度因素。文献[26]提出一种基于决策树模型的空战态势评估方法,能够快速对空战态势进行分类,但是决策树中节点属性的排序受样本影响较大。由于模糊推理在描述模糊信息时具有独特的优势[14,22-23],通过设计推理规则,能够将模糊的、难以描述的空战态势信息转化为确定性的推理结果,因此本文提出了一种基于模糊推理的视距空战机动决策方法。
1 UCAV机动决策建模
1.1 空战场景描述
现代空战由感知和攻击两个重要部分组成,感知主要是指获取敌机及战场态势信息,解决的是“看”的问题;攻击是指对敌机发射空空导弹,解决的是“打”的问题,因此空战机动决策是一个“边看边打”的过程,即感知和攻击相互耦合。机动决策属于攻击范畴,但很大程度上依赖于战场态势信息和目标信息的感知结果。本文的空战场景为1vs.1近距格斗空战,在近距格斗场景下假设战场态势感知等级为全局透明态势,即空战双方均可以获取对手高精度、高刷新率的态势信息,依据透明的态势信息可以辅助UCAV对敌机的意图及位置做出预测。空战双方为红蓝UCAV,红方代表我机,蓝方代表敌机,双机携载相同类型的近距空空导弹。空战双方做出合理的机动决策尽可能构成发射条件同时避免落入对手的导弹不可逃逸区。空战场景如图1所示。

图1 空战场景示意图Fig.1 Diagram of an air combat scene
1.2 空战机动决策流程
UCAV利用感知能力获取空战态势信息和敌机状态信息。通过态势信息,计算角度、距离、速度及高度的优势因子;同时根据模糊规则,对空战态势进行评估,将空战态势输入模糊推理机,从而自适应地调整优势函数中各因子的权重。优势因子与自适应权值相结合构成机动决策的目标函数。在机动决策时,利用决策机动、序列机动和惯性机动相结合的方法预测敌机位置。最后根据决策算法,选择使空战优势函数最大化的机动动作,完成机动决策,并更新空战态势。空战机动决策流程如图2所示。
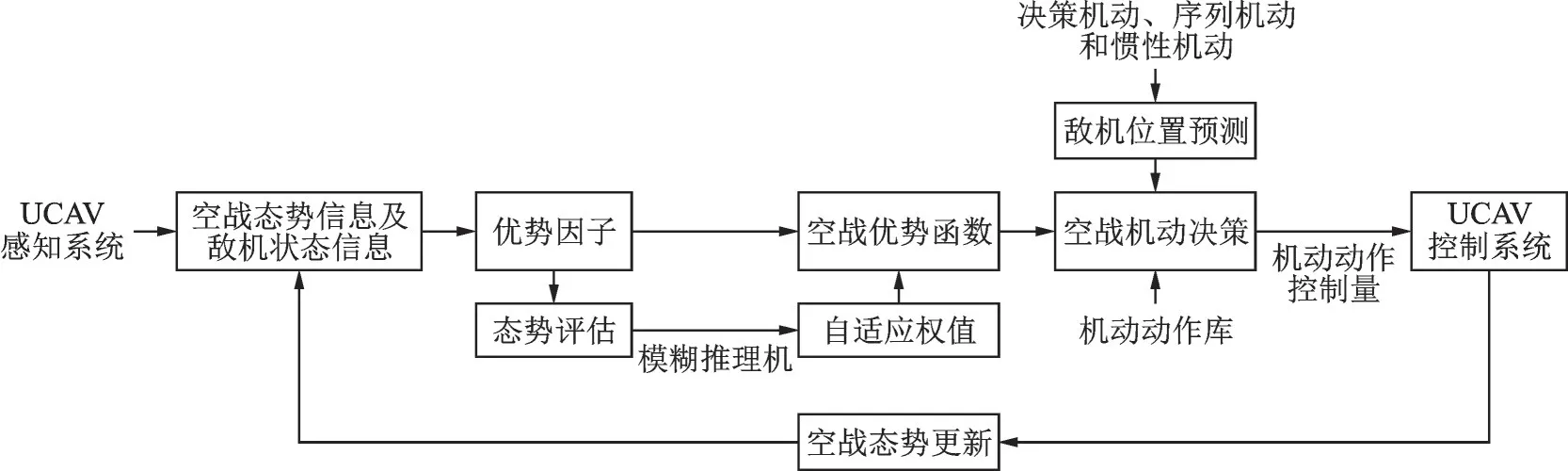
图2 空战机动决策流程Fig.2 Air combat maneuver decision process
1.3 UCAV运动模型
在本文中,UCAV指具有自动驾驶仪的固定翼无人机,在惯性坐标系中建立飞机三自由度运动模型[25],并用质点模型描述UCAV的运动学方程为
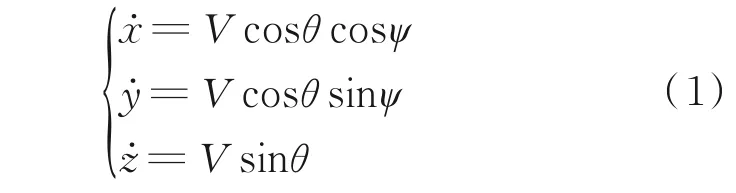
为了简化,假设飞机在无侧滑中飞行,同时推力矢量方向、速度矢量方向及机头指向3者始终保持一致,则在航迹坐标系中UCAV的动力学方程为

式中:x、y、z分别为无人机的质心在惯性坐标系中的坐标;V为机体坐标系中无人机的速度大小;θ、ψ分别为惯性坐标系中无人机的俯仰角、偏航角;g为无人机的重力加速度;nx、ny、γ分别为切向过载、法向过载以及由升降舵和副翼耦合控制的滚转角。切向过载与无人机的阻力和油门控制的发动机的推力有关,其方向为机头方向;法向过载与升力有关,其方向为机身对称面内垂直于机头方向。因此控制模型的状态向量为S=[x,y,z,V,θ,ψ],控制向量为C=[nx,ny,γ]。本文中定义姿态角的取值范围均为[-π,π],其中偏航角右偏为正,滚转角右滚为正,俯仰角抬头为正,法向过载机身对称面内向上为正,切向过载机头方向为正。UCAV的动力学模型如图3所示。

图3 UCAV动力学模型示意图Fig.3 Schematic diagram of UCAV dynamics model
在已知飞机初始状态和控制向量的情况下,根据四阶龙格库塔方程,即可求解式(1,2)中的微分方程,从而得到飞机的运动状态。为了保证UCAV在飞行过程中的可靠性,状态量和控制量必须满足如下限制

1.4 UCAV机动动作库
根据UCAV的飞行状态,文献[13-14]提出了7种基本机动动作,组成UCAV的机动动作库,分别为匀速平飞、最大过载加速、最大过载减速、最大过载爬升、最大过载俯冲、最大过载左转弯、最大过载右转弯。但是这与实际的UCAV飞行并不完全相符,UCAV难以持续采用最大过载飞行。因此,为了更真实地反应UCAV的机动动作,本文将平飞、爬升、俯冲、左转弯、右转弯5种基本机动动作丰富为匀速、加速、减速机动,最终机动动作库被扩充为15种。在空战过程中,UCAV的复杂机动动作如螺旋爬升,蛇形机动、眼镜蛇机动等均可由15种基本机动动作组合而成。机动动作库的名称及控制向量如表1所示。

表1 机动动作库Table1 Names and control vectors of maneuver action library
1.5 敌机位置预测
在空战机动决策中,对敌机位置的预测将对空战结果产生重要影响。空战战场瞬息万变,更加强调空战决策的实时性,同时机动决策要有一定的前瞻性,因此需要UCAV能够快速准确地预测敌机可能到达的位置。为了降低敌机位置预测模型的复杂度,本文在文献[25]的预测模型上进行改进,将敌机的机动视为3部分组成,分别是决策机动、序列机动和惯性机动。决策机动是指当前态势下敌机具有一定的智能,自主决策对我机优势最大的机动动作。序列机动是指控制向量保持不变的机动动作。机动动作在一段时间序列内可以认为是恒定的,在一个完整的机动动作中UCAV不倾向于突然的改变机动动作,如盘旋机动可视为连续的转弯机动,筋斗机动可视为连续的爬升机动等。惯性机动是指UCAV在惯性作用下不施加任何控制量,即UCAV有保持惯性的倾向,可将其视为平飞机动。UCAV在飞行过程中平飞占比最大,2个机动动作之间需要有平飞机动作为衔接,只有当战术需要时才会改成平飞状态。在敌方飞机的机动决策上,本文认为决策机动在3种机动中占比最高,敌方总倾向于选择当前态势下最有利于增加优势的机动动作。基于以上分析,得到敌机的预测位置为

式中:pe为敌机的预测位置;p1代表敌机做惯性机动后的位置,控制量为平飞机动;pk代表敌机做序列机动后的位置,控制量与敌机的上一机动动作保持相同;ps代表敌机做决策机动后的位置;ω1、ωk、ωs代表对应机动动作的权重系数。因为ps代表决策机动,所以ωs的权重要比ω1、ωk更大。
2 基于模糊推理的空战态势评估模型
2.1 空战优势因子
在空战中UCAV根据获取的战场态势信息来做出机动决策,因此对战场态势信息进行合理的建模将对决策结果产生重要影响。空战态势信息可以用态势向量Θ表示,Θ=(A,R,V,Δz)。A指代敌我方位,R指代由敌方位置坐标指向我方位置坐标的距离矢量,V代指UCAV的速度,Δz表示高度差,具体指红方高度减蓝方高度。其中敌我方位信息A由两部分组成,分别是目标方位角α1和目标进入角α2。α1指以R为基准到敌机(蓝方)速度矢量Vb的夹角,α2指以R为基准到我机(红方)速度矢量Vr的夹角。本文规定α1和α2均取正角度,其取值范围为[0,π]。态势向量Θ如图4所示。

图4 空战态势向量Fig.4 Air combat situation vector
2.1.1 角度优势因子
设角度优势因子为μA(α),表达式为


式中:下标为r的代表我机参数,下标为b的代表敌机参数。从式(5)可以看出,当我机处于敌机尾后攻击态势时,角度优势取得最大值1;当我机处于被敌机咬尾态势时,角度优势取得最小值0。图5显示了角度优势为0和1时的空战场景示意图。

图5 角度优势为0和1时空战场景示意图Fig.5 Schematic of the air combat scenario when the angle advantage is0and1
2.1.2 距离优势因子
设距离优势因子为μR(|R|)。假设UCAV的不可逃逸区 为[Rmin,Rmax],Rmin代 表不可逃逸区距离下界,Rmax代表上界,只有当两机距离|R|∈[Rmin,Rmax]时导弹才有可能击中目标。因此,设定距离优势因子为

当敌机处于我机导弹不可逃逸区之内时,距离优势取得最大值1,当超出导弹不可逃逸区时距离优势关于两机距离呈正态分布。
2.1.3 速度优势因子
设速度优势因子为μV(|V|)。在定义速度优势因子前首先需要定义UCAV最佳攻击速度|V*|,当敌机处于我机导弹不可逃逸区之内时,最佳攻击速度|V*|取敌机速度|Vb|,当敌机处于导弹不可逃逸区之外时应进行加速或者减速来使敌机尽快进入不可逃逸区,因此|V*|表示为

则速度优势因子μV(|V|)可以表示为

2.1.4 高度优势因子
设高度优势因子为μH(Δz),设敌我双方UCAV高度差为

为了占据发射导弹时的高度优势,我机必然要提升Δz,设定最佳高度差是一段区间[h*,h*+σh],当Δz处于该区间时高度优势因子均取得最大值1。因此,高度优势因子表达式为

综上,综合分析角度、距离、速度、高度4种优势因子,UCAV的空战综合优势为

式(15)被称为UCAV空战优势函数,式中ωA、ωR、ωV、ωH分别代表角度、距离、速度、高度4种优势因子的权重。传统的空战态势评估研究中,更多的是比较敌机优势值μb和我机优势值μr的大小,通过两者的差值μr-μb来反应我机空战优势的大小。但是当两机优势值都非常小时用差值很难真实地体现两机优势的差距,因此选用两机优势函数的比值μ′来反映我机对敌机的优势,表达式为

式(16)被称之为机动决策函数。就红方而言,式中μr代表红方每个机动动作对蓝方预测机动的优势,μb代表蓝方的预测机动对红方每个机动动作的优势。式(16)的物理意义就是红方UCAV从机动动作库中选择下一个决策时刻机动决策函数最大的机动动作。
2.2 模糊推理介绍
式(15)中优势函数的权重因子随空战态势的变化而发生变化,目的是建立一个随空战态势而变的动态优势函数,从而更好地指导UCAV做出机动决策。空战是一个高对抗性、高复杂性的过程,文献[25]将空战态势划分为我方优势、我方劣势、共同安全和共同危险4种,并在4种空战态势下设计了不同的变权重优势函数。但是空战态势反映的是敌我关系,往往是充满模糊性、动态化、多样化的,因此文献[25]中的4种空战态势难以全面地描述战场态势,并且在态势划分时只考虑了角度和距离因素。
模糊决策是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法,其特点是评价结果不是绝对地肯定或否定,而是以一个模糊集合来表示。同时,模糊决策可以根据专家控制经验制定相应的决策规则,决策过程中输出参数可随输入的变化在一定范围内动态调整,具有更好的多样性、动态性和适用性。因此本文用模糊决策的方法来确定变权重优势函数中的权重因子。完整的模糊决策流程通常由输入输出变量模糊化、设计隶属度函数、建立模糊规则库及解模糊等步骤组成。
2.3 基于空战态势的模糊推理机设计
(1)输入输出模糊化及隶属度函数设计
基于空战态势的模糊推理机共有4个输入,4个输出,输入为角度、距离、速度、高度优势因子,输出为角度、距离、速度、高度权重因子。依据专家经验,各输入输出的模糊语言子集如下所列。
①角度模糊优势因子

②距离模糊优势因子

③速度模糊优势因子

④高度模糊优势因子

⑤角度、距离、速度、高度权重因子

式中:PB、PM、M、NM、NB、IN、OUT、P、N均为模糊语言,代表对应输入输出的模糊化表示;下标i分别代表A、R、V、E;ωi代表解模糊后的精确输出量;ωˉi代表模糊输出量,EA、ER、EV、EH分别代表模糊化后的输入量。式(17~21)中既包含了各输入输出的模糊量,又包含了各模糊量的隶属度函数。本文全部采用矩形隶属度函数和单点隶属度函数,即各输入量对应某一模糊量下的隶属度仅为0或1,且同一输入量的各隶属度函数之间无交集,这样做是为了降低模糊推理计算的复杂度,便于根据模糊规则快速进行输入到输出的映射,符合空战实时性的要求。
(2)模糊推理规则设计
依据专家经验,得到树状的模糊推理规则如图6所示,其中共包含32条推理规则,依次编号为Wi(i=1,2,…,32),下标i表示第i条规则,同样对应32种空战态势。

图6 模糊规则树Fig.6 Fuzzy rule tree
模糊规则的制定遵循了如下专家经验:①当我方UCAV在某一模糊优势因子上出现了明显短板时要尽可能地选择弥补该短板的机动动作来迅速增加我方优势。如态势W2下,我方UCAV在角度、距离、速度上均占据优势,但是高度上却处于劣势,因此在进行机动决策时应该增加高度优势的权重。②当角度优势较大时应该持续增加角度优势,以希望迅速构成空空导弹的发射条件。如态势W10下,我方UCAV角度优势较大,同时高度处于劣势,因此在进行机动决策时不只要迅速提升高度,更要增加角度优势,希望我方UCAV在角度上能够达到较大优势。③当我方UCAV角度优势小或较小时,应该采取逃逸策略,尽可能地增加高度优势,减小距离优势,目的是增大与敌方UCAV的距离,从而逃离敌方的导弹不可逃逸区。如态势W20下,我方UCAV角度不占优势,同时有距离优势,这时的机动决策应该摈弃距离优势,转而增加高度和速度优势。
(3)解模糊得到优势函数权重因子
根据模糊规则,输出的模糊量需要去模糊化转换为精确量,本文采用重心法去模糊化[27],表达式为

式中:μ(z)为输出量z所在模糊集合的隶属度函数;z0为模糊推理得到的精确量。z0的范围可能和实际输出的数值范围不一致,还需要进行论域变换,如式(11)所示。

式中:k=(umax-umin)/(zmax-zmin)为比例分子;[umin,umax]为实际控制量的变化范围;[zmin,zmax]为z0的变化范围。
综上,从模糊推理机的输入量得到输出量的具体过程如下:
步骤1根据式(17~21)中的隶属度函数将精确输入量转化为模糊输入量。
步骤2根据图5模糊规则树中包含的32条规则,将模糊输入量映射为模糊输出量;由于本文所设计的各输入的不同模糊量隶属度函数间并无交集,因此无需进行复杂的模糊蕴含关系计算即可由模糊输入量映射得到模糊输出量。
步骤3根据式(22~23),计算解模糊后的精确输出量,得到当前空战态势下的优势函数权重因子ω,表达式为

式中优势函数权重因子ω的物理意义为UCAV选择机动动作的倾向性。
2.4 机动决策算法
机动决策时采用试探机动的方法,即基于敌机的位置预测和态势评估模型,我方UCAV依次遍历机动动作库,并对机动动作执预行之后的机动决策函数进行计算,选取决策函数值最大的机动动作,将其作为当前时刻的决策机动。敌方UCAV采用同样的决策算法,但是敌方UCAV选择决策机动的概率为1.4 小节中的ωs,同时还分别有ω1、ωk的概率选择惯性机动和序列机动。
为了衡量红蓝双方的空战优势,本文设计了一个空战裁判系统,根据裁判函数μc来判断红蓝双方的胜负。μc代表了UCAV4种优势因子的总和,表达式为

不同于式(15)中的UCAV空战优势函数,由于UCAV要根据当前空战态势适应性地做出最有利于己方的机动动作,因此UCAV空战优势函数中优势因子的权重应随态势变化。但是就裁判系统而言,红蓝双方综合优势的评判标准在各种空战态势下应保持统一,因此将裁判函数中各优势因子设置为等值定权重。同时,本文将裁判函数作为空战结束的中断条件,当有一方UCAV的综合优势达到指定阈值c时空战结束,代表该UCAV获胜。
机动决策算法的伪代码如下。
(1)初始化任务参数
(2)foriin range(total_step):
(4) 空战结束
(5)else:空战未结束(式(23))
(6) 根据当前空战态势,利用模糊推理机,计算红蓝UCAV优势函数中的权重因子
(7) 红 方UCAV位 置 预测,蓝方UCAV位 置预测(式(4))
(8) 红方UCAV计算试探机动后空战态势,蓝方UCAV计算试探机动后空战态势(式(15))
(9) 红方UCAV选择机动动作,蓝方UCAV选择机动动作(式(16))
(10) 红方UCAV执行机动动作,蓝方UCAV执行机动动作(式(1,2))
(11) 空战状态更新(式(1,2))
(12)i+=k
在伪代码中,i代表空战时长,k代表UCAV的机动动作执行时长,total_step代表设定的空战总时长,和代表红蓝UCAV的空战综合优势,c代表空战结束的综合优势阈值。
3 仿真实验及结果分析
为了验证本文方法的有效性,本节对其进行仿真验证。仿真环境为AMD-RYZEN5,主频2.60 GHz,16GB内存,基于Python3.7 为平台进行仿真实验。实验初始化参数如表2所示。

表2 空战仿真实验初始化参数Table2 Initialized parameters of air combat simulation experiment
在仿真实验中,红蓝双方UCAV战场信息的感知能力、武器性能及飞机机动性能均相同。
3.1 实验一:机动动作库对机动决策的影响
本实验为了比较机动动作库对UCAV空战能力的影响,红方UCAV采用本文设计的机动动作库,包含15种机动动作,蓝方UCAV采用文献[13]的机动动作库,包含7种机动动作。红方UCAV的 初 始 状 态 向 量Sr=[0,0,7000,200,0,-π/2],即初始位置坐标为(0,0,7000),初始速度200m/s,初始俯仰角为0,初始航向角为-π/2。蓝方UCAV的初始状态向量Sb=[0,5000,7800,200,0,-π/2],即初始位置坐标为(0,5000,7800),初始速度200m/s,初始俯仰角为0,初始航向角为-π/2。空战轨迹如图7所示。

图7 场景1空战轨迹图Fig.7 Air combat trajectory diagram of scenario1
初始状态红蓝UCAV处于均势状态,但是蓝方UCAV高度上占优,因此红方UCAV选择爬升,迅速弥补高度上的劣势,蓝方UCAV采用左转弯并进行俯冲,期望将高度优势转化为速度优势。紧接着红方UCAV向蓝方UCAV一侧斜拉起并进行小半径右转弯,迅速将机头对准敌机获取角度优势并进行俯冲,保持角度优势的同时增加速度优势,而蓝方UCAV的转弯半径较大,航向调整较慢,最终红方UCAV的综合优势率先达到阈值,红方取得空战胜利。整个空战过程中红蓝UCAV综合优势的变化图如图8所示。

图8 场景1红蓝UCAV空战综合优势变化图Fig.8 Graph of red and blue UCAV air combat comprehensive advantage of scenario1
仿真实验结果表明,采用扩充后的机动动作库能够增加UCAV在空战中的机动性,从而根据空战态势迅速地达到优势占位,达到先敌制胜。
3.2 实验二:态势评估模型对机动决策的影响
本实验为了验证本文态势评估模型在机动决策中的有效性,红方UCAV采用本文提出的基于模糊推理的态势评估模型,蓝方UCAV采用文献[21]提出的基于贝叶斯网络的态势评估模型。红方UCAV的优势函数共有32种动态权值,蓝方UCAV的优势函数共有4种动态权值。红蓝双方的机动动作库中均包含15种机动动作。
设计两轮仿真实验。第1轮令红方UCAV初始时刻处于被蓝方UCAV咬尾的劣势状态。红方UCAV的初始状态向量Sr=[3000,0,6500,200,0,-π/2],即初始位置坐标为(3000,0,6500),初始速度300m/s,初始俯仰角为0,初始航向角为-π/2。蓝方UCAV的初始状态 向 量Sb=[5000,5000,6500,100,0,-3π/4],即初始位置坐标为(5000,5000,6500),初始速度100m/s,初始俯仰角为0,初始航向角为-3π/4。空战轨迹如图9所示。

图9 场景2空战轨迹图Fig.9 Air combat trajectory diagram of scenario2
从空战轨迹中看出,初始时刻红方UCAV被蓝方UCAV咬尾,但是由于红方速度较快,蓝方速度较慢,所以蓝方虽占据优势但是达不到空战结束条件。在被动态势下,红方首先选择做加速平飞机动进行逃逸,目的是迅速增大和蓝方的距离,脱离对手的导弹射程,而蓝方选择继续尾随红方,试图保持现有优势。但是红方占据速度上的优势,因此在脱离蓝方的导弹最大射程后选择进攻型机动,迅速爬升,紧接着做出了半筋斗翻转机动,并对准敌机进行俯冲将高度优势转化为速度优势,而蓝方UCAV做出的机动决策明显要滞后于红方UCAV,面对对手的进攻没有做出及时的机动决策,也同样进行俯冲希望弥补初始状态时速度上的劣势,最终红方UCAV的综合优势率先到达阈值,空战以红方的胜利而告终。整个空战过程中红蓝UCAV综合优势的变化图如图10所示。

图10 场景2红蓝UCAV空战综合优势变化图Fig.10 Graph of red and blue UCAV air combat comprehensive advantage of scenario2
第2轮令蓝方UCAV初始时刻处于被红方UCAV咬尾的被动状态。红方UCAV的初始状态向量Sr=[0,3000,7000,100,0,3π/4],即初始位置坐标为(0,3000,7000),初始速度100m/s,初始角为0,初始航向角为3π/4。蓝方UCAV的初始状态向量Sb=[5000,1000,7000,300,0,π],即初始位置坐标为(5000,1000,7000),初始速度300m/s,初始俯仰角为0,初始航向角为π。空战轨迹如图11所示。

图11 场景3空战轨迹图Fig.11 Air combat trajectory diagram of scenario3
在蓝方UCAV初始状态处于劣势的情况下选择了采取右转弯加俯冲的机动动作,而红方UCAV由于初始速度慢因此选择加速平飞机动,试图增加速度优势来达到全面优势。蓝方UCAV虽然企图逃逸,但是目的性不强,所做出的机动反应没有很好地达到逃逸效果,最终红方UCAV的综合优势率先达到阈值,空战以红方UCAV的胜利而告终。整个空战过程中红蓝UCAV综合优势的变化如图12所示。
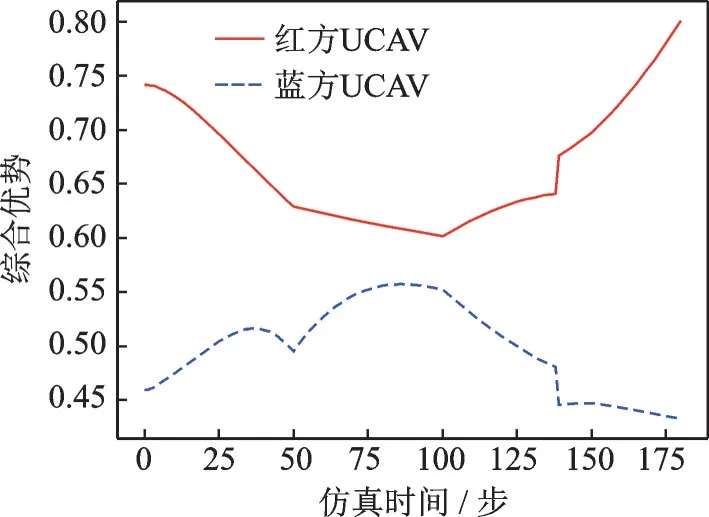
图12 场景3红蓝UCAV空战综合优势变化图Fig.12 Graph of red and blue UCAV air combat comprehensive advantage of scenario3
通过对实验二中2轮仿真结果的对比可得,基于模糊推理的态势评估模型与基于贝叶斯网络的抗战态势评估模型相比更能提升UCAV的机动决策能力。因为前者模型中涵盖的空战态势种类更多,更能全面地反应实时的战场态势,从而有助于指导UCAV做出更加具有针对性的机动决策。
4 结 论
(1)通过对UCAV的机动决策进行建模,设计机动动作库,引入敌机位置预测模块,并利用模糊推理机从角度、距离、速度、高度4个方面对空战态势进行评估,实现了UCAV在近距空战场景下的自主机动决策;
(2)改进后的机动动作库与传统机动动作库相比,能够增加UCAV在近距空战中的机动性能,使机动决策能力提升;
(3)利用基于模糊推理的态势评估模型,设计了32种优势函数动态权重,更加全面地描述空战态势,指导UCAV做出更有针对性的决策,提升了自主空战能力。
同时,本文还有以下不足:(1)空战模型未对UCAV空空导弹不可逃逸区进行建模,没有考虑真实的导弹不可逃逸区对UCAV空战能力的影响;(2)在敌机的意图推断方面仅仅考虑了位置预测,而在真实空战中敌机的意图可能包含欺骗、干扰、战术协同等更高级的行为,因此与真实的UCAV空
战还有一定差距;(3)在机动过程中未考虑考虑舵机、作动器的位置及速率限制等约束条件。在后续研究中,应该引入导弹不可逃逸区和更加高级的敌机意图推断,增加空战模型的真实性,同时应该考虑从单机机动决策向多机协同战术决策转变。
