基于MSD和ICCP改进的地磁联合匹配算法

付希禹，孙永荣，李荣冰

（南京航空航天大学自动化学院导航研究中心，南京 211106）

现代军事复杂环境下，航空器的无线电信号很容易受到屏蔽和干扰，导航基站本身也容易被攻击［1］。惯性导航系统是目前运用最多的自主式导航系统，然而其误差随时间积累，无法保持长航时高精度工作。因此，相关研究转向寻找一种自主式、隐蔽性强的导航定位方式。

地磁场是分布于全球的矢量场，地球近地空间内任意一点的地磁矢量都与该地点的经纬度一一对应。因此，理论上确定一点的地磁矢量即可实现全球定位［2］。地磁导航作为一种无源自主导航，具有全天时、全天候、隐蔽导航等特点，相比于惯性导航系统，其误差不随时间积累，因此在飞行器控制、卫星自主定轨、导弹制导和水下导航定位等领域具有重要的军事价值和广阔的应用前景［3］。

地磁导航依据对数据处理方式的不同，可分为地磁匹配和地磁滤波。地磁匹配导航原理如图1所示，载体移动运行中磁传感器采集一组数据序列，同时，惯性导航系统给定位置参考，并从数据库中拾取相应位置的地磁值序列。将两组序列通过算法检验匹配程度，从而确定载体位置。匹配结果可作为组合滤波观测输入，校正惯导系统，也可作为系统定位结果输出［4］。其中，地磁匹配算法可分为两类，一类是基于相似度度量的等值线匹配（Contour matching，CM）算法，一类是最近等值线迭代（Iterated closest contour point，ICCP）算法。

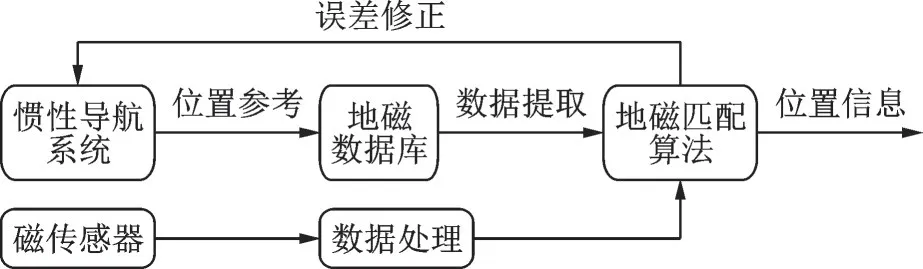
图1 地磁匹配导航原理Fig.1 Principle of geomagnetic matching navigation

CM算法原理简单，运算速度快，对初始误差要求低，应用范围广泛。常见CM算法包括平均绝对差（Mean absolute different，MAD）算法、均方差（Mean square difference，MSD）算法、积相关算法、归一化积相关算法、Hausdorff算法等［5-7］。但由于CM算法是采用平动搜索方式进行序列匹配，因此不能校正航向误差。

ICCP算法中涉及刚性变换，相比于相似度算法，它可以进行图形的旋转操作，使修正轨迹更为逼近真实轨迹，可有效修正航向误差。因此，在存在航向误差时，其精度明显优于相似度算法。ICCP存在以下不足：①初始误差，即实际轨迹与惯导指示轨迹的误差不能过大，否则会出现发散，甚至误匹配；②在等值线变化平缓的地图范围内，会出现明显的误匹配现象。③迭代过程需获得指定长度采样序列，实时性较差。

针对以上问题，周贤高等［8］从匹配区域选取角度出发，将粗糙度、地磁熵等概念应用至数字地磁图，进行特征区域选配；黄斌等［9］采用实时迭代评价的方式，避免了地磁匹配需要预先指定匹配数据序列长度的困难；Chen等［10］利用多维磁场分量差异信息作为目标函数进行最优路径查找，提出地磁矢量匹配算法，有效地解决了ICCP算法在航迹附近存在多条等值线时误匹配的问题。

以上两种算法匹配策略不同，应用广泛、成熟，但受其各自原理性缺陷制约，在存在航向误差、初始误差较大的应用场景下往往定位效果不佳。因此，本文分析利用已有两类经典算法的优势，采用粗精结合策略，并在此基础上引入动态窗口技术，提出了一种基于MSD和ICCP改进的地磁联合匹配算法。

1 改进的地磁联合匹配算法

结合上述分析，为充分利用两类经典算法的优势，本文提出的改进地磁匹配算法的匹配策略可分为粗匹配和精匹配两部分。粗精结合是一种先采用快速匹配算法确定载体模糊匹配位置，随后采用高精度算法减小最终匹配误差的匹配策略。文献［4，11-12］分 别 提 出 了 基 于Hausdorff和ICCP、TERCOM和ICCP、地形熵和ICCP等直接结合的算法，这种方法虽然在一定程度上可提高匹配精度，但也明显加长了匹配计算时间；同时，载体移动运行过程中，序列点不断延长，待采样点达指定序列长度时进行一次匹配位置修正，随着序列长度增加，其相同时间内修正轨迹输出频率较低，算法实时性和搜索效率都会受到影响。因此，需对组合算法中的过程进行相应改进以改善其性能。

本文粗匹配选取一组磁场测量序列和惯导指示序列，利用MSD算法快速得到粗匹配轨迹，进而约束精匹配过程搜索范围并缩小初始误差；精匹配过程采用动态窗口算法，每次动态窗口根据轨迹误差实时调整窗口范围，检索指定区域，并在匹配完成后根据收敛性输出匹配结果。

1.1 粗匹配

MSD是一种基于均方差的相关匹配算法，其思想为载体携带的磁传感器采集磁场信息测量值序列，由惯导指示轨迹在地磁库中平动搜索遍历搜索区域，根据性能指标确定测量值序列和参考值序列的相关度，最终得到最优匹配序列。MSD算法相较其他CM算法，匹配精度高、运算量小，因此作为快速匹配算法更为合适，其相关度函数为

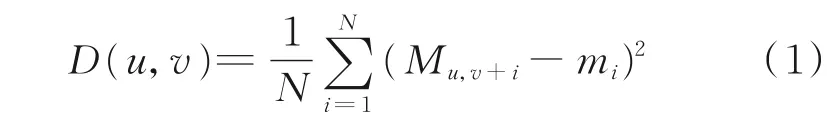
式中：Mu，v+i表示位置(u，v)上数据库基准值；mi表示磁传感器测量值，使得D(u，v)最小的序列即为粗匹配结果。

地磁数据库范围Rx×Ry，分辨率为Δx×Δy（x表示经度方向，y表示纬度方向），拾取N个连续惯性导航系统指示序列点及其磁传感器测量值，如图2所示，标记为第n次拾取，并采用快速MSD方法对地磁库搜索区域进行平动遍历搜索。

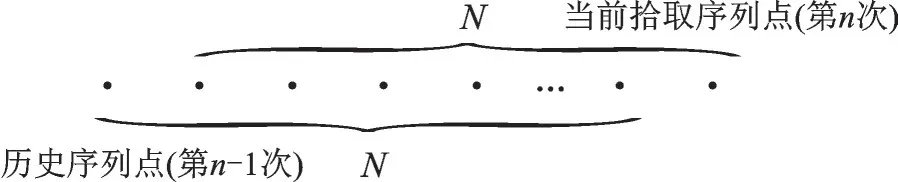
图2 序列点拾取示意图Fig.2 Schematic diagram of selecting sequence

由于ICCP算法在应用时初始误差不应过大，因此，在上述范围内对该N个连续点采用MSD算法可以确定载体模糊位置，使得惯导指示轨迹变换至真实轨迹附近，从而避免该问题。但由于算法本身原理制约，经MSD算法处理后的轨迹仍存在航向误差，因此该轨迹必须经过进一步修正，才能保证输出结果精度。

1.2 精匹配

精匹配过程中考虑算法复杂度及时间成本，提高搜索效率，提出一种动态窗口算法进行区域选定和搜索。该动态窗口具有两层含义：第一，窗口位置是动态的，是与载体移动方向一致并同步移动的；第二，窗口范围不是固定不变而是根据误差范围动态变化的，从而最大效率地提高匹配精度。算法的具体流程如下：

（1）确定动态窗口

快速粗匹配确定真实轨迹模糊位置后，根据该结果进一步约束精匹配搜索范围，避免不必要的非选配区域搜索，并减小最终匹配误差。将上述粗匹配后N个连续点记为第n个动态窗口，惯导指示轨迹序列为Gn={g(i)n}，处理后轨迹序列为Pn={p(i)n}，i=1，2，…，N，惯性导航系统与粗匹配后序列的经度、纬度方向误差分别为δx、δy，经纬区间长度 分 别 为Lx、Ly，则 第n个 窗 口 范 围 为Nx×Ny，如图3所示，其中

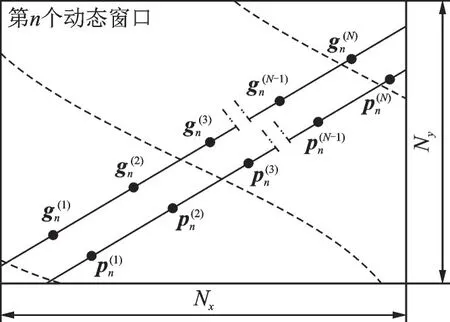
图3 动态窗口示意图Fig.3 Schematic diagram of dynamic window

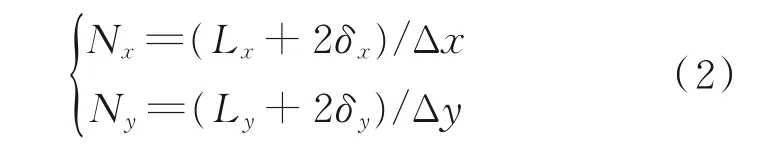
根据动态窗口范围从Rx×Ry区域内提取地磁基准值。

（2）轨迹修正

从上述窗口内提取B={B(i)n}的地磁等值线，寻找等值线上距离处理后轨迹序列Pn={p(i)n}最近的点Qn={q(i)n}，并求解它们之间的刚性变换关系

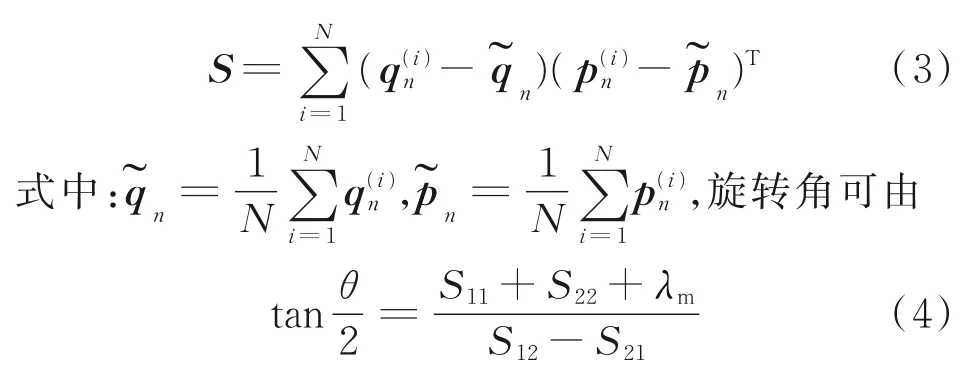
解算得出，λm为矩阵S特征值的最大值。因此，由式（3，4）求得刚性变换的旋转矩阵R和平移矩阵t为

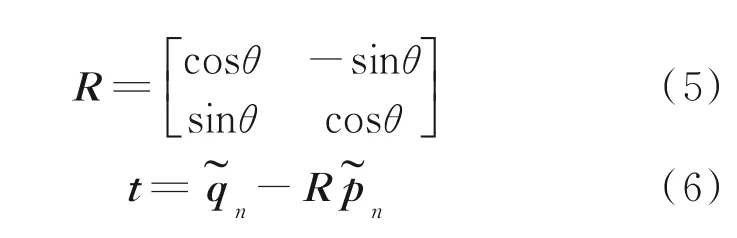
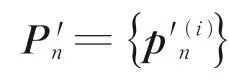
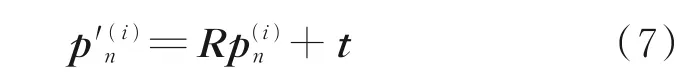
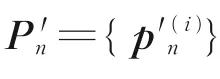
（3）更新匹配序列

序列数仍为N个保持不变重新拾取轨迹点，重复上述步骤。改进的地磁联合匹配算法流程如图4所示。

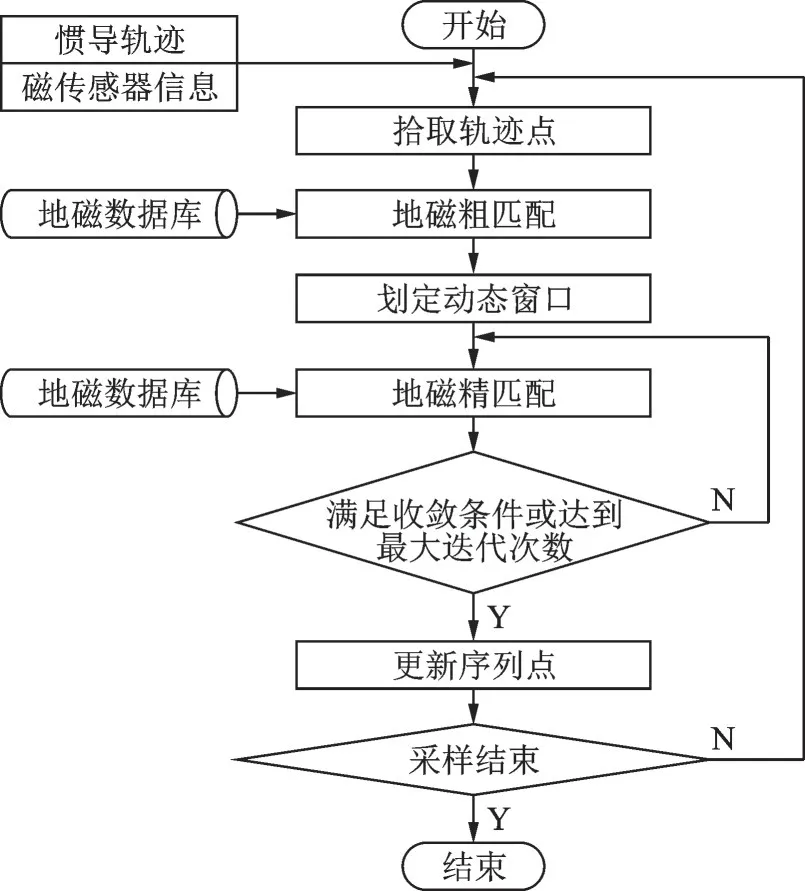
图4 地磁联合匹配算法流程图Fig.4 Flow chart of geomagnetic united matching algorithm

2 仿真实验与分析

为验证本文算法有效性，进行如下仿真实验。仿真实验地磁图是基于卫星、船舶、机载的地磁测量结果编制的海拔在大地水准面以上4km处的EMAG2地磁异常数据构建，其初始分辨率为二弧分［13］。地磁异常场在局部区域变化复杂，地磁信息丰富，更适合作为地磁导航的基准图，然而受成本、时间等因素限制，其分辨率达不到精密导航要求。因此，上述地图经Kriging空间插值后作为地磁异常数据库，经度范围119.00 °E～119.99 °E，纬度范围32.00 °N～32.99 °N，网格大小100×100，分辨率0.01 °×0.01 °，存放于导航计算机中。

首先进行一组算法正确性实验，仿真图如图5（a）所示。考虑一航空器匀速定高飞行，预设启用地磁匹配辅助惯导时航迹起点为119.15 °E，32.05 °N，其实际航迹以“△”表示；惯导初始位置误差（0.1 °，0.1 °），航向误差5.0 °，在硬件参数为Inter（R）i7-10700F CPU2.90 GHz处 理 器、16GB RAM的计算机，基于MATLAB R2018a编程环境进行仿真试验，以验证本文算法在惯导存在大初始误差和航向误差时的有效性，指示轨迹如图中“○”所示。实验结果如图5（b，c）和表1、2所示。

由图5所示，从匹配精度方面来看，经过粗匹配后，惯导指示轨迹移至真实轨迹附近（图中“×”所示），经纬各方向匹配精度得到大幅提升，但与真实轨迹之间存在一定差距，不仅存在位置误差，还存在航向误差，此时的匹配结果无法作为最终的结果输出；经过动态窗口算法精匹配校正后（图中“★”所示），航向误差得到修正，如表1所示，经向位置误差下降了约20.8 %，纬向位置误差下降了约23.7 %。

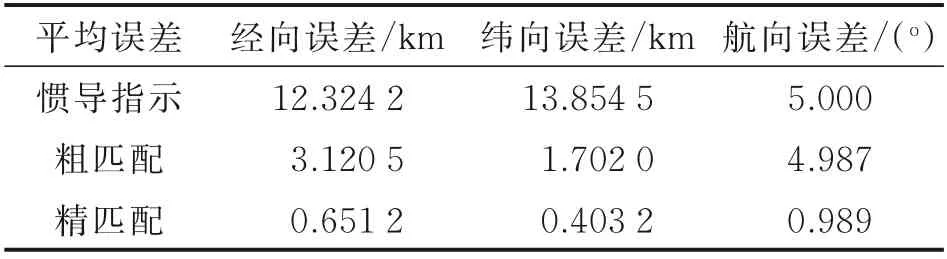
表1 算法误差对比Table1 Comparison of algorithm error

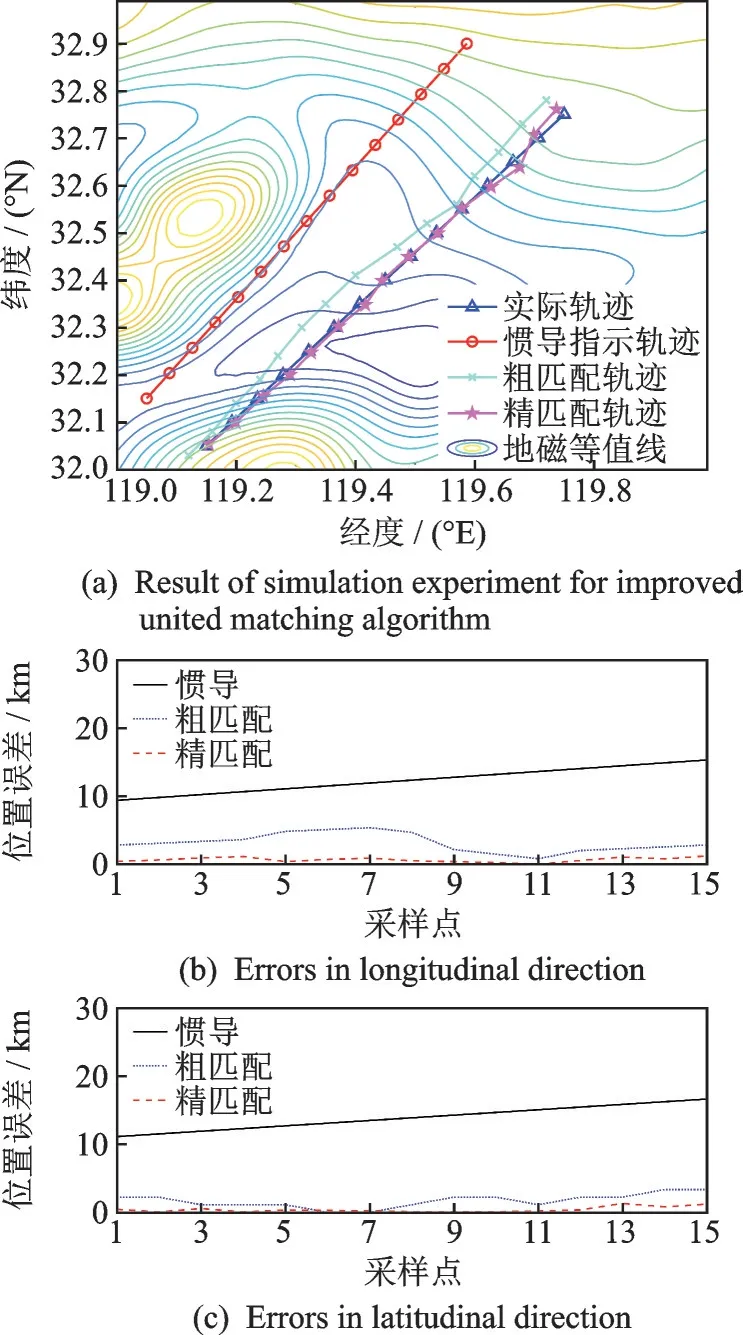
图5 仿真实验结果图Fig.5 Result of simulation experiment

从算法实时性来看，经典算法每采集指定数量序列点后，进行一次匹配输出修正轨迹，在匹配点数未达到精度要求时，其输出存在一定延迟，每2.575 s才能获得一次位置更新；而本文提出的改进算法将算法时间分散在各窗口中，进行了9次位置信息输出，对惯导输出实现单点迭代，准确跟踪真实轨迹，在保证匹配精度前提下，其实时性显著提高。

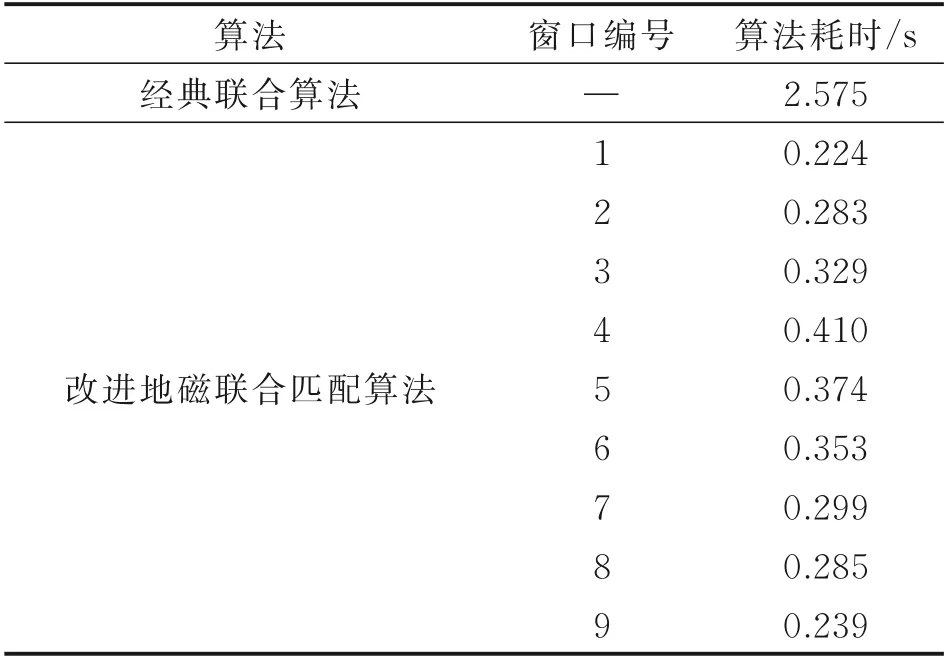
表2 算法实时性实验结果对比Table2 Comparison of algorithm real⁃time performance

相同仿真条件下，进行本文算法与两类经典算法等采样序列精度对比实验，并将算法修正后与修正前的误差比值记为修正率，作为精度评价指标，其实验结果如图6、表3所示。

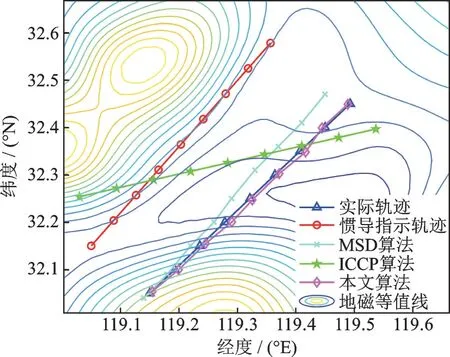
图6 等采样序列算法精度对比实验Fig.6 Accuracy comparison experiments of different algorithms under the same sampling sequence

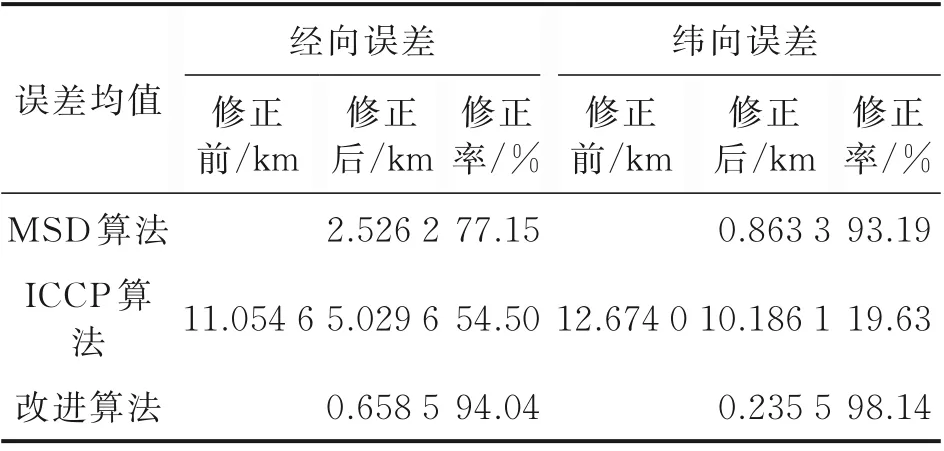
表3 等采样序列算法精度对比Table3 Accuracy comparison of different algorithms under the same sampling sequence

由图6可以发现，MSD算法（图中“×”所示）匹配轨迹与实际轨迹之间仍存在角度，体现出MSD算法在航向误差校正中的劣势；同样，ICCP算法（图中“★”所示）对初始误差较敏感，其校正轨迹明显偏离实际轨迹。此仿真条件下两类经典算法均精度较低、不可靠。通过表3可知，相比而言，改进地磁联合匹配算法经、纬向误差修正率分别可达94.04 %和98.14 %，具有更好的校正效果，从而进一步表明了该算法的有效性。

3 结 论

为进一步提高地磁匹配导航的精度，改善地磁匹配算法在航空器存在航向误差和大初始误差场景下的应用效果，本文综合分析比较了CM算法和ICCP算法两类经典算法的优劣势，提出了一种基于MSD和ICCP改进的地磁联合匹配算法，即采用粗精结合的策略，确定精匹配过程的搜索范围并缩小初始误差，并在精匹配阶段采用动态窗口算法，提高算法实时性和搜索效率。仿真实验结果表明，本文提出的改进地磁联合匹配算法可有效结合两者的优势，克服了MSD算法不能校正航向误差、ICCP算法在初始误差较大的情况下算法发散和实时性较差的问题，有效地提高了地磁匹配导航的匹配精度和效率。