基于排队论的终端区航班进场时间预测

赵嶷飞，乔晓莹

（1.中国民航大学空中交通管理学院，天津 300300;2.中国民用航空局空中交通管理局航行情报服务中心，北京 100102）

环绕大型枢纽机场的终端区，是降落航班的汇聚点也是起飞航班的发散点，交通密集，交通态势复杂［1］。由于空域容量与交通流量失衡所导致的终端区空域拥堵和航班延误问题越发严重［2］。当起降航班量超过终端区的可用空域容量时，终端区内及周围空域中就会出现大量盘旋等待航班，与进离场航班相互影响，造成巨大的安全风险。与此同时，终端区高密度交通流也会给空中交通管制员带来巨大工作负荷，管制员不得不对外发出流量控制，限制机场起飞航班数量和外部空域进入终端区航班数量，由此造成更大范围的航班延误。

终端区进场时间预测作为交通管理的前提和基础，一直是空管领域国内外研究的重点。对该问题最早的研究思路是借助航空器运动学模型或者统计规律对进场时间做出预测。1999年，Fablec等［3］利用神经网络，基于机型和高度限制对进场航迹进行预测。2013年，Hamed等［4］使用回归统计算法进行航迹预测，与基于质点模型的航迹预测结果比较表明：回归统计算法的航迹预测结果更为准确。2014年，Tastambekov等［5］使用局部线性函数回归算法，在仅考虑历史雷达轨迹而不使用任何物理参数或航空参数的情况下对中短期的航迹进行预测。2014年，张军峰等［6］基于航空器性能数据，采用航空器意图模型与航空器动力和运动学模型相结合的方法对进场航迹进行预测。在单机航迹 解算基础上，2015年，Hong等［7］引入聚类算法结合概率信息来预测航空器的进场时间。机器学习算法兴起后，也很快应用于该问题研究。2015年，陈强等［8］使用径向基函数神经网络构建航空器进场参数与进场飞行时间的映射关系，基于正交最小二乘算法构建并训练径向基函数神经网络，对终端区航班进场飞行时间进行预测。2016年，郑志祥等［9］从影响航空器飞行时间的因素出发，采用随机森林算法构建航空器到达时刻预测模型，从而实现对航班到达时刻的预测。2018年，李阳等［10］基于航迹数据，使用最小二乘支持向量机方法，建立航班进场时间预测模型，以咸阳机场为例的研究结果表明，预测结果的均方根误差可控制在11s。

上述研究普遍基于单机航迹分析，虽然取得了较大进展，但从交通流管控角度看，仍然存在较大改进空间。例如：数据处理量和计算量较大；当天气、军航活动等不确定性情况出现时，数据较为分散。事实上，从交通流管控角度看，掌握进场交通流整体规律，提供平均进场时间更为直接、有效。此外，基于数据方法获得的模型适用性较差，面临新的终端区和运行环境其适用性是值得商榷的。

针对这些不足，从交通流管控角度，本文将提出基于排队论的航班进场时间预测模型，抓住进场交通流的整体流动特征，如终端区排队长度和终端区内的平均飞行时间，以及对应的管制工作负荷水平。基于这一模型，不仅有望降低现有模型难度，而且可以为改善管制工作带来更直接的指导建议。

1 问题描述

排队论［11］是由丹麦数学家Erlang创立的，经过几十年的发展，排队论的理论基础日渐完善，当前广泛应用于交通系统及其他服务系统。民航作为交通系统的一部分，排队论自然也可以应用于该领域。解决排队问题的目的是：研究系统运行效率、评估系统服务质量、确定系统参数最优值以及研究系统改进措施等［12］。当顾客的到达率大于服务率时，就会出现排队现象。排队系统的一般模型如图1所示。

图1 排队系统的一般模型Fig.1 General model of queuing system

如图1所示，顾客从顾客源出发，到达服务机构前需排队等待接受服务，服务完成后离开。概括来看排队系统由3个基本部分组成：（1）到达过程；（2）排队规则；（3）服务机构。到达过程指顾客是按什么样的规律到达排队系统；排队规则指到达服务机构的顾客如何进行排队；服务机构指包括服务台数量、服务方式及服务时间分布在内的服务台情况。在航空运输过程中有多个航班进离场时，终端区通常就会有排队现象的产生。因此，可以将终端区视为一个排队系统。终端区航班进场的示意图如图2所示。

图2 终端区航班进场的示意图Fig.2 Schematic diagram of flight arrival in terminal area

航班在脱离航路后首先需要理顺航路与进近的关系，通过调整高度、速度对准进场点。当进场航班量过大时，后续航班需要执行等待程序排队进场，此时在进场排序和计量区域（Arrival sequencing and metering area，ASMA）边界的进场点就会形成等待队列。这里可以将进场航班作为顾客源，航班到达ASMA区域边界进场点的过程为输入过程。航班从进场点进场后沿着进场程序飞向起始进近定位点（Initial approach fix，IAF），并通过调整外形、减小速度到达中间进近定位点（Intermediate approach fix，IF），最终在最后进近定位点（Final approach fix，FAF）对准着陆航迹进行着陆。这里可以将ASMA区域边界进场点到跑道的空域作为服务台，按照先到先服务的原则为进场航班提供服务，航班从进场点进场至从跑道离开所经历的时间为服务时间。此外，当驾驶员认为不能安全着陆时，需要在复飞进近点（Missed approach point，MAPT）进行复飞，航班上升到复飞程序公布的转弯点（Turning point，TP）后可转向指定的航向或位置。需要注意的是，本文的排队模型暂且不考虑复飞航班。

为了简化分析，本文将终端区航班进场过程建模为一个单队-单服务台的排队系统。如图3所示，航班在40海里的ASMA区域边界进行排队，等待接受从ASMA区域边界到跑道的引导服务。快速准确的终端区航班进场时间预测，可以帮助空中交通管制员尽早发现进场时间变长、进场效率降低的航班，从而提前制定应对措施，及时加以改进。

图3 终端区排队系统简化图Fig.3 Simplified diagram of terminal area queuing system

本文对终端区航班排队进场时间预测模型做出以下假设：

（1）航班总体无限，单个到达且相互独立；

（2）终端区采用等待制排队规则；

（3）终端区排队系统的容量无限；

（4）终端区为单队-单服务台模式；

（5）航班到达排队队列后，终端区服务机构以先到先服务的方式提供服务。

基于上述假设，图4展示了终端区航班进场时间预测计算过程。

图4 终端区航班进场时间预测计算过程Fig.4 Calculation process of flight arrival time prediction in terminal area

终端区航班进场时间预测详细步骤如下：

步骤1数据处理与选取。筛选有效的航班进场数据，选择高峰时段进场航班数据进行分析。

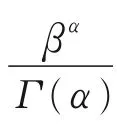
步骤4建立预测模型。基于航班到达规律分布和服务时间分布，选择适用的排队模型来建立终端区航班进场时间预测模型。

步骤5分析所建模型的预测效果。将进场航班数据分为训练集和测试集，用训练集获得模型参数，用测试集进行测试，得到预测误差。

2 数据选取

本文将以天津滨海国际机场终端区为例，建立排队模型对航班进场时间进行预测，使用的数据为广播式自动相关监视（Automatic dependent surveillance-broadcast，ADS-B）数据。将ADS-B数据与飞行计划（Flight plan，FPL）数据进行匹配，选取天津滨海国际机场2017年8月的进场航班数据作为研究数据。此外，由于排队大多发生在高峰期，为找到高峰时段，本文以航班进入40海里ASMA区域边界的时间作为开始进场时间，统计了8月31天中以1h为单位的各时间段的进场航班总数，如图5所示。

图5 2017年8月天津机场各时段累计进场航班数Fig.5 Cumulative number of arrival flights at Tianjin Airport in each period in August2017

3 排队论模型

在8月的31天中，不同时间段的累计进场航班数差别较大。05：00～06：00时段31天累计进场航班数最少，只有22架次，平均每天该时段进场航班小于1架次。13：00～14：00时段的累计进场航班数量高达375架次，为累计进场航班数最高的时段。本文最终选取高峰时段12：00～14：00的航班数据进行航班进场时间预测分析，并以15min为单位将该时间段划分为8个更小的时间段。在8月的31天中，以15min为单位的高峰时间段的累计进场航班数如图6所示。

图6 2017年8月以15min为单位的高峰时段累计进场航班数Fig.6 Cumulative number of arrival flights during peak hours at an interval of15min in August2017

3.1 航班到达规律分布

对于终端区排队系统，航班到达40海里的ASMA区域边界的过程为输入过程，在该过程中航班的到达是单个到达且相互独立的；航班的到达数只与时间区间的长短有关；并且在充分小的时间间隔内两个或两个以上航班同时到达进场排队队列的概率极小。可见，航班到达满足泊松流的3个条件。因此，本文以高峰时段13：15～13：30的进场航班数据为例，对航班的到达规律进行Poisson分布拟合，使用样本数据对未知参数进行估计，并进行卡方（χ2）［16］检验判断进场航班的到达是否服从Poisson分布。表1给出了13：15～13：30时段航班到达数的统计，图7给出了航班到达规律Poisson分布的拟合。

图7 航班到达规律Poisson分布拟合Fig.7 Poisson distribution fitting of flight arrival

表1 13 :15～13:30时段航班到达数的统计Table1 Statistics of flight arrivals during13:15—13:30

由图6可见，以15min为单位，所选高峰时段12：00～14：00的31天累计进场航班数均在72架次以上。其中，13：15～13：30时段的31天累计进场航班数高达112架次，相当于在一天中的该时段，15min进场约3.6 架次。2017年全国民航航班运行效率报告中公布的天津机场小时容量为31架次/h［15］，相 当 于 进 场 容 量 为15.5 架 次/h，若 以15min为单位，则进场容量为3.8 架次/15min。可见，高峰时段13：15～13：30的进场航班数已十分接近天津机场的进场容量。

如图7所示，直观上看以15min为单位的航班到达规律基本符合Poisson分布。为了准确证实以15min为单位的航班到达规律是否服从Poisson分布，需要进一步进行卡方检验，所以进行如下假设。

H0：15min时段到达航班数服从Poisson分布；

H1：15min时段到达航班数不服从Poisson分布。

表2 卡方统计量计算过程Table2 Chi‑square statistics calculation process

3.2 航班服务时间分布

航班的服务时间为航班进入终端区服务系统40海里ASMA区域边界到着陆所经历的时间。同样，以13：15～13：30时段的航班数据为例，对航班的服务时间进行Gamma分布拟合。采用极大似然估计法［17］对Gamma分布参数进行估计，得到α=18.9855 ，β=6.4238 。图8、9分 别 为 服 务 时 间Gamma分布拟合、服务时间和Gamma分布累积概率图。

图8 服务时间Gamma分布拟合Fig.8 Gamma distribution fitting of service time

图9 服务时间和Gamma分布的累积概率Fig.9 Cumulative probability of service time and Gamma distribution

3.3 进场时间预测模型

基于本文的假设和前面章节对航班到达规律分布及服务时间分布的分析，将采用一般服务时间M/G/1排队模型［18］来建立终端区航班进场时间预测模型，即航班输入过程服从Poisson分布，航班的服务时间服从一般分布，终端区为单服务台排队服务系统，终端区的容量无限，进场航班数目无限。

在一般服务时间M/G/1模型中，到达过程假设为泊松过程，Pollaczek-Khinchine公式提供了稳定状态下系统中队列长度（Ls）的表达式

式中：ρ为服务器的服务强度；Var[T]为服务时间的方差。

让λ表示为单位时间内到达的顾客数，进一步可得到顾客在系统中的逗留时间（Ws）的表达式为

最终，航班预计到达时间（TArrival）可表示为

式中TASMA为航班到达ASMA区域边界的时间。

4 预测结果分析

本 文 使 用2017年8月1日 至27日12：00～14：00时段的实际航班运行数据作为训练集，构建终端区航班进场时间预测模型，获得模型参数的估计值。然后利用所建立的模型对8月28日至31日的航班进场时间进行预测，并用实际航班运行数据对预测结果进行检验。各时段的分布结果如表3所示。

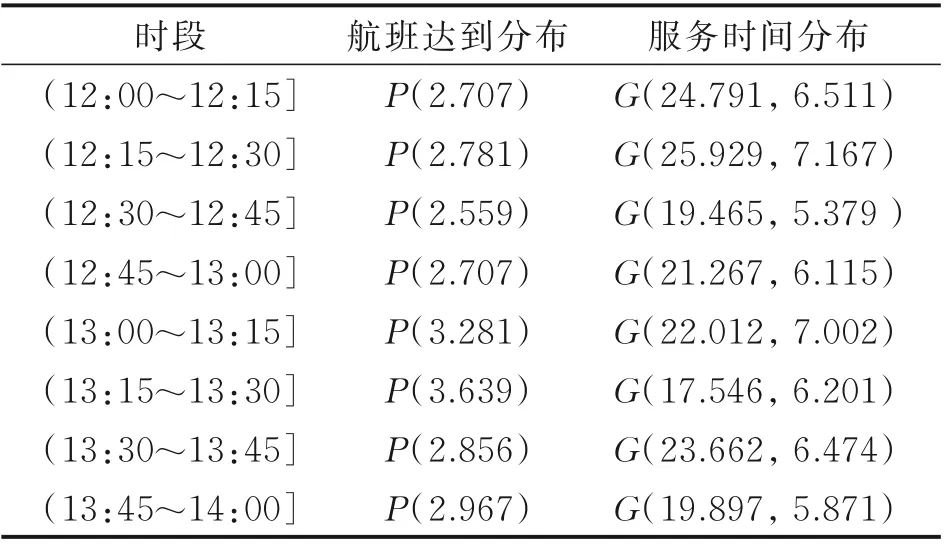
表3 8月1～27日高峰时段航班到达分布和服务时间分布Table3 Distributions of flight arrivals and service time during peak hours from August1to27

不失一般性，对各时段的航班到达是否符合Poisson分布以及服务时间是否符合Gamma分布均进行了卡方检验。检验结果表明，8月1日至27日12：00～14：00的8个 时 段 的 航 班 到 达 均 服 从Poisson分布，服务时间均服从Gamma分布。使用训练集来获得模型的参数，基于本文建立的预测模型对8月28日至31日相应时段的航班进场时间进行预测。

图10展示了8月28日至31日的航班进场时间的预测结果，可见预测的航班预计到达时间与航班实际到达时间吻合度较好。为了对预测结果进行进一步的评估，下面将具体对每一个预测日各时段航班的实际进场时间均值和预测进场时间均值进行对比分析（见图11），并分别计算每一个预测日航班进场时间预测值与实际值的平均绝对误差（Mean absolute error，MAE）。

图10 8月28日至8月31日预测结果Fig.10 Forecast results from August28to August31

如图11所示，每个预测日各个时段航班平均预测进场时间与平均实际进场时间变化趋势基本一致，大部分时段的平均预测值与平均实际值较为接近。有些时段的预测结果与实际值相差较大，可能与该时段的进场航班数较少有关。航班进场时间预测的MAE如表4所示。

表4 进场时间预测的平均绝对误差Table4 MAE of arrival time prediction

图11 实际进场时间和预测进场时间比较Fig.11 Comparison of actual arrival time and predicted arrival time

由表4可见，以15min为单位的高峰时段进场时间预测的平均绝对误差在1min左右，表明建立的终端区航班进场时间预测模型较为可靠，预测结果较为准确。

进一步基于天津机场实际数据，提出一个针对天津机场的进场时间预测模型。首先，对以15min为单位的96个时段模型参数进行识别，以期获得96个时段的航班进场时间预测值。但在实际计算过程中发现，当以15min为单位的31天累计进场航班数小于等于39架次时，模型预测误差较大。考虑到这些时段的进场航班数较少，航班无须排队，可将航班进场时间用畅通进场时间近似。畅通进场时间是指在非拥挤条件下航班在ASMA区域的通行时间［19］，中国民用航空局在计算畅通进场时间时选取40海里ASMA区域范围内实际飞行时间的20%分位数［15］。按此方法，可得天津机场的畅通进场时间为13.13 min。另外，对以15min为单位的31天累计进场航班数大于39架次的时段利用所建模型进行航班进场时间预测。然后，以1h为单位对预测结果取平均值，获得天津机场以1h为单位的航班进场时间预测值。最后，根据每日各时段的平均进场航班数得到与进场航班数对应的进场时间预测结果，预测结果如表5所示。

当管制员已知天津机场的预计小时进场航班数时，就可以根据表5中相应的预测值快速地预测出航班预计到达时间。虽然本文所建模型的预测结果相比基于单机航迹的预测结果误差较大，但它大大降低了预测模型的难度，它的简单性使得笔者可以对航班进场时间进行快速预测，有助于为改善管制工作带来更直接的指导建议。

表5 与进场航班数对应的进场时间预测结果Table5 Forecast results of arrival time corresponding to the number of arrival flights

5 结 论

为实现终端区航班进场时间的快速预测，本文将终端区视为服务台、进场航班视为顾客，对终端区进场航班建立一般服务时间M/G/1排队模型，并以天津滨海国际机场为例，利用所建立的M/G/1排队模型对高峰时段终端区航班进场时间进行预测。预测结果表明，以15min为单位的航班进场时间预测平均绝对误差在1min左右，预测结果与实际结果较为接近。最后基于天津机场实际数据，提出一个针对天津机场的进场时间预测模型。根据预测结果，空中交通管制员可以根据预计小时进场航班数来快速预测航班预计到达时间，尽早发现进场时间过长、进场效率低的航班，从而提前采取应对措施，以确保航班的正常运转。本文所建模型降低了现有模型的难度，可以为空中交通管制员提供更好、更及时的态势感知，从而达到减轻管制员工作负荷、提高航班运行安全和终端区航班运行效率的目的。在未来如何把天气因素考虑到终端区航班进场时间预测中，以及采用其他机器学习方法构建进场时间快速预测模型，将会成为研究的重点。