柯西不等式的改进及其应用

胡晓莉，乔龙坤

（江汉大学 人工智能学院，湖北 武汉 430056）

柯西—布涅柯夫斯基不等式是异于均值不等式的另一个重要不等式。它在数学学科分支中有着极其广泛的作用，如线性代数中的矢量、概率论与数理统计中的方差、高等数学中的积分等等［1］。正是因为柯西不等式在许多数学学科里有较为广泛的应用［2］，因此引起数学家们的兴趣，多年来数学工作者们对柯西不等式的研究从未停止［3－4］。其在不同领域中有着不一样的形式，因此也产生了诸多推广的形式。在n维欧氏空间中，对任意的两个向量α,β，记其内积为(α,β)，则有(α,β)2≤(α,α)(β,β)，当且仅当α,β线性相关时等号成立，这就是著名的柯西－布涅柯夫斯基不等式。特别地，当考虑的欧式空间为n维实数空间Rn时，则对向量α＝(a1,a2,…,an)，β＝(b1,b2,…,bn)∈Rn，有著名的柯西不等式为

1 柯西不等式序列的构造

设x＝(x1,x2,…,xn),y＝(y1,y2,…,yn)为欧氏空间Rn中的两个向量，记矩阵

定理1 设M如矩阵（2）所示，令mk＝CS(Mk)＋∑M－∑Mk，则有非递增序列为

证明 由下列事实

从矩阵M中的元素及顺序主子矩阵Mk和Mk＋1中的元素及式（3）可得

用柯西不等式后与M中绿色框外的所有数直接求和，则有m1＝∑M；m2表示对红色框中的数之和用柯西不等式后与M中红色框外的所有数直接求和，即

同理

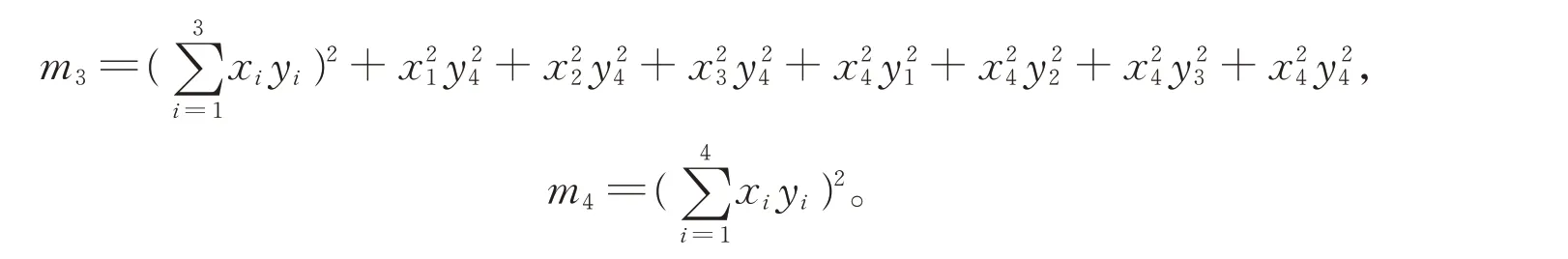
显然有，(x,x)2(y,y)2＝m1≥m2≥m3≥m4＝(x,y)2。

事实上，定理1 中的不等式序列还可以进一步优化。设M͂k为矩阵M中选定任意不同的k行k列按原来的顺序构成的主子矩阵，则由定理1 可得如下结论。

下面我们将引进凸函数来构造第二个柯西不等式序列。设fk(v)＝vmk＋1＋(1－v)mk，其中0 ≤v≤1。易知，fk(v)为单调递减函数，故有mk＋1＝fk(1) ≤fk(v) ≤fk(0)＝mk。故结合定理1 和fk(v)的单调性，可得以下推论。

推论2 令fk(v)＝vmk＋1＋(1－v)mk，则有下列非递增序列

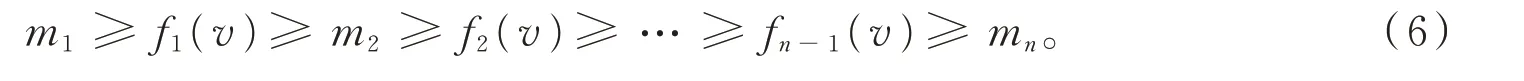
2 基于方差乘积的酉不确定性关系

图1 两个算子的基于方差乘积的不确定性界比较Fig.1 Comparison of variance product-based uncertainty bounds for two operators

3 结语

本文首先定义了矩阵和函数以及柯西函数，运用以低维柯西不等式来优化高维柯西不等式的思想得到了第一个柯西不等式序列。然后，构造基于柯西不等式的凸函数，得到了另一个不等式序列。最后，将所构造的不等式序列应用于解决两个酉算子的基于方差乘积的量子不确定性实例中。结果表明本文所构造的柯西不等式序列确实能有效改进基于方差乘积的量子酉不确定性的界。