基于LabVIEW 的二自由度直升机姿态控制策略

刘志强，叶 曦，钱同惠

（江汉大学 智能制造学院，湖北 武汉 430056）

0 引言

二自由度直升机是微型无人机中较为常见的机型，常被应用于航拍、军事侦察以及无人机快递等多个领域［1－2］。在研究直升机控制过程中，直升机作为控制对象，具有很强的非线性和耦合性，使得直升机的稳定性和操纵性较差［3］。控制系统是直升机运行的关键，它对增强直升机稳定性和操作性有着重要作用。因此，设计合适有效的控制系统，研究更精准的控制方法，对直升机整体性能的改善有着较强的现实意义。

王怡怡等［4］研究了二自由度直升机姿态角控制的自抗干扰控制方法，从理论上保证了该控制方法的有效性，但并没有运用到实物中进行验证；孙雨佳等［5］设计了模糊PID 控制方法，有效改善了控制系统的性能，但未有效解决直升机系统的高耦合性；王博［6］采取线性化和极点配置的方法，设计出状态反馈控制器，解决了强耦合问题；赵文豪［7］运用LQR 控制策略对直升机实验系统的控制器进行设计，实验结果显示，对于强耦合系统，LQR 控制器基本可以满足系统的跟踪控制要求。

通过分析以上文献可知，状态反馈控制器对于二自由度直升机的姿态控制具有较强的解耦性和适用性。本文利用Quanser AERO 直升机实验平台，提出了一种基于LabVIEW 平台实现的状态反馈控制方法。LabVIEW 平台拖拽式的编程方式相较于MATLAB 编程更为灵活简单，良好的可视化操作界面能让用户根据需求进行系统参数设定，大大提高了工作效率［8－11］。本文在二自由度直升机实验平台上，通过控制俯仰和偏航两个方向角来研究直升机姿态控制方法，实验结果表明，利用LabVIEW 平台能够实时跟踪直升机俯仰角和偏航角变化，验证了LQR 控制器的信号跟踪性能，解耦性能较好。

1 二自由度直升机系统总体结构

1.1 系统组成

直升机模型的主要构件有基座、俯仰枢轴、偏航枢轴、螺旋桨等，实物结构如图1 所示。基座作为一个托台，双桨在其上进行俯仰和偏航运动。左右螺旋杆分别安装在桨的两端，其中螺旋杆底部分别安装两个无芯直流电机。当两端螺旋桨旋转时，产生升力使系统做俯仰运动；当左右螺旋桨存在电压差时，可以使系统做偏航运动。

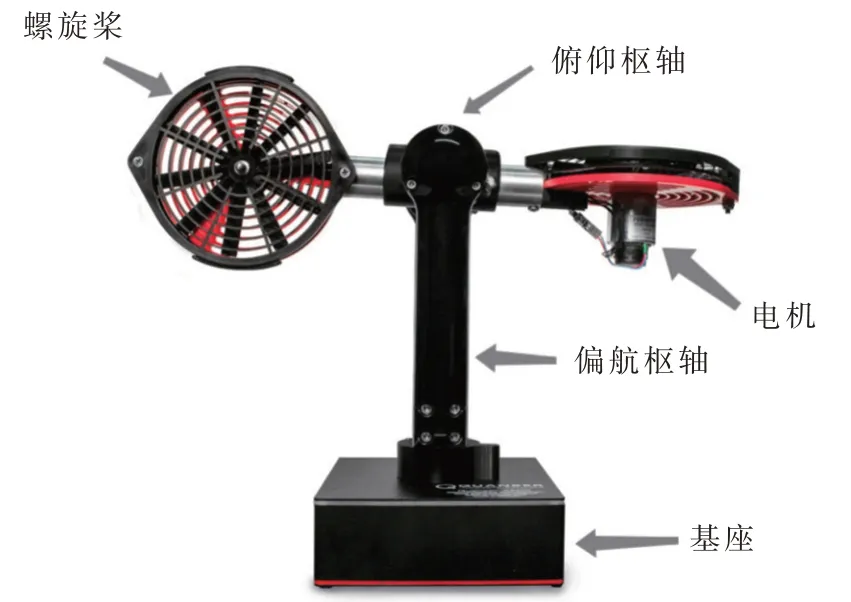
图1 二自由度直升机结构图Fig.1 Structure diagram of the two-DOF helicopter

直升机系统的动力来源于电机工作，其电机电枢电路原理图如图2 所示。直流电机轴与螺旋桨轮毂连接，轮毂是一种夹头夹钳，用于将螺旋桨安装到电机上，具有转动惯量J1。螺旋桨连接输出端，转动惯量为J2。相关符号参数信息详见表1。

表1 符号参数信息Tab.1 Symbol parameter information

图2 电机电枢电路原理图Fig.2 Schematic diagram of the motor armature circuit

反抗电动势电压eb与电机轴转速ωm以及电机反电动势常数km有关，其表达式为

将空气阻力所施加的扭矩简化为与电机转矩相反的阻力矩τd，其表达式为

本文直升机系统俯仰角度与偏航角度的测量是通过对编码器的脉冲进行计数实现的，得到的角度数据传输到控制卡中，进而实时获取俯仰运动和偏航运动信号。编码器的型号参数详见表2。

表2 编码器的型号参数Tab.2 Encoder type parameters

1.2 系统动力学模型

二自由度直升机动力学模型的建立需要分析其机械结构和受力情况，采用微分方程的形式来表示。实验自由体模型如图3 所示。

图3 实验自由体模型Fig.3 Experimental free-body model

模型使用如下约定：

1）当俯仰角为零时，直升机与水平地面平行。

2）当俯仰运动产生力Fp，机身围绕Y轴逆时针运动时，俯仰角变大，即θ˙＞0。

3）当偏航运动产生力Fy，机身围绕Z轴逆时针运动时，偏航角变大，即ψ˙＞0。

4）当俯仰转子电压Vp＞0 时，俯仰角θ˙＞0。

5）当偏航转子电压Vy＞0 时，偏航角ψ˙＞0。

考虑到俯仰和偏航运动过程中的耦合情况，可建立如下微分方程。当机身与水平地面平行时，运动方程为

在俯仰和偏航轴上作用的扭矩为

式中，Jp、Jy分别表示俯仰方向和偏航方向转动惯量，kg·m2；Dp、Dy分别表示俯仰轴和偏航轴的阻尼，V·s/rad；Ksp表示俯仰轴的刚度，N·m/rad；Kpp、Kyy分别表示俯仰转子和偏航转子的扭矩推力增益，N·m/V；Kpy表示偏航转子在俯仰上作用的交叉扭矩推力增益，N·m/V；Kyp表示俯仰转子在偏航上作用的交叉扭矩推力增益，N·m/V；Vp、Vy分别表示施加在俯仰转子和偏航转子上的电压，V。

本文考虑到受控对象非线性特征明显，设计出有效的控制方法需要得到直升机整体的数学表达式，通过变换函数模式，化简得到运动方程的状态空间表达为

本次实验在二自由度直升机系统平台上经过测试得到相关物理参数见表3。在进行数据测量和计算过程中会使各项参数存在一定误差，但是误差范围不会对控制系统的研究产生太大影响。

表3 二自由度直升机物理参数Tab.3 Physical parameters of the two-DOF helicopter

2 控制器设计

传统PID 控制在非线性系统的线性化模型上很适用，但它不考虑俯仰运动和偏航运动的强耦合。因此，该控制方法有一定的缺陷，无法满足预期控制目标。利用上述建模给出的状态空间模型，可以采用LQR 算法设计状态反馈控制器，改善控制系统的耦合性。LQR 可以求得状态反馈的最优控制规律，它以状态方程形式给出线性系统，目标函数是对象状态和控制输入的二次型函数［12］。本文使用最优线性二次型跟踪调节理论对二自由度直升机俯仰轴和偏航轴进行控制器设计。

2.1 系统的可控性分析

系统可控性描述的是给定系统的任意初始状态，存在控制矢量使得有限时间内可以把系统所有的状态引向零状态。

可控性的判别常采用秩判据，其充分必要条件是n维矩阵A和B组成的n维矩阵Gc秩为n，其中Gc＝[B AB A2B…An－1B]。

根据表3 各项参数可求得

把A和B代入Gc中，可计算出4 维矩阵Gc。通过使用MATALB 软件调用rank（ctrb（A，B））可以得到Gc的秩为4，即矩阵Gc满秩，所以系统是可控的。

2.2 系统的可观性分析

系统可观性描述的是通过输出估计系统可能的输入，可观性判别的充分必要条件是n维矩阵A和B组成的n维矩阵Go秩为n，其中Go＝[C CA CA2…CAn－1]T。

同理，把A和B代入Go中，可计算出4 维矩阵Go的秩。通过使用MATLAB 软件调用rank（obsv（A，C））可以得到Go的秩为4，即矩阵Go满秩，所以系统是可观的。

通过上述分析可以得出，该系统具备可控性和可观性，故而采用LQR 控制方法具备可行性。

2.3 最优跟踪控制

首先，重写直升机系统的状态空间方程

构造一个状态反馈控制器：

则该系统的最优跟踪控制指标为

式中，K为状态反馈增益，xd为系统期望跟踪轨迹，Q和R均是正定对称矩阵。

由于该系统满足可控性和可观性，为使（8）式取得极小值，有输出的近似最优跟踪控制方程为

Riccati 矩阵代数方程为

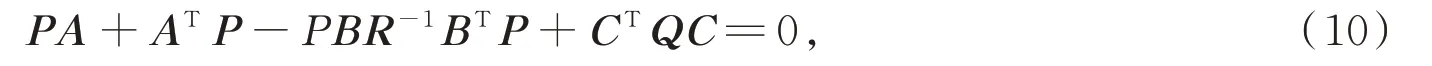
式中，P是（10）式的唯一正定对数解，常量伴随阵

闭环控制系统的状态方程为

通过上式及初始条件x(0) ＝x0，即可求出近似最优轨迹ẋ(t)。

3 仿真实验分析

通过对所设计控制策略进行仿真分析，可以进一步理解LQR 控制器的设计思路，同时对二自由度直升机实验系统的动力学方程进行进一步验证。

在实验过程中，首先测试PID 的控制效果，并求得相关参数。经过多次调整参数进行实验对比发现，选取比例系数Kp＝10，积分系数Ki＝0.5，微分系数Kd＝1 时，系统的动态性能和稳态性能更好。具体实验步骤如下：

俯仰轴自由，偏航轴固定，在阶跃信号作用下得到俯仰轴30 s内的输出响应，实验结果如图4所示。

图4 PID 控制俯仰轴输出阶跃响应Fig.4 Step response of PID controlled pitch axis output

俯仰轴固定，偏航轴自由，在阶跃信号作用下得到偏航轴30 s内的输出响应，实验结果如图5所示。

图5 PID 控制偏航轴输出阶跃响应Fig.5 Step response of PID controlled yaw axis output

俯仰轴自由，偏航轴自由，同时设置俯仰轴和偏航轴跟踪一个近似正弦波信号，其中俯仰轴正弦信号是一个幅度值为0.5 rad、周期值为2.5 s、脉冲幅度为50%周期值，跟踪时长20 s；偏航轴正弦波信号是一个幅度值为1.2 rad、周期值为5 s、脉冲幅度为50%周期值，跟踪时长30 s。实验结果如图6 和图7 所示。

图6 PID 跟踪俯仰轴性能Fig.6 Pitch axis performance of PID tracking

图7 PID 跟踪偏航轴性能Fig.7 Yaw axis performance of PID tracking

由图6 和图7 可以观察到PID 控制同时跟踪俯仰轴和偏航轴效果不佳，与期望曲线有较大差距。其中俯仰轴主要是信号存在一定延迟，响应过慢；而偏航轴受强耦合影响严重，输出信号完全无法满足期望信号要求。

另采用LQR 控制器进行测试，同时设置俯仰轴和偏航轴跟踪一个近似正弦波信号，其中俯仰轴正弦信号是一个幅度值为0.5 rad、周期值为20 s、脉冲幅度为50%周期值，跟踪时长20 s；偏航轴正弦波信号是一个幅度值为2.5 rad、周期值为25 s、脉冲幅度为50%周期值，跟踪时长30 s。

在LabVIEW 软件中构建基于LQR 控制策略的二自由度直升机仿真程序，如图8 所示，通过前面板定义系统的Q矩阵和R矩阵。

图8 LabVIEW 程序框图Fig.8 LabVIEW program block diagram

图9 LQR 跟踪俯仰轴性能Fig.9 Pitch axis performance of LQR tracking

图10 LQR 跟踪偏航轴性能Fig.10 Yaw axis performance of LQR tracking

传统PID 控制受强耦合影响严重，无法准确跟踪俯仰轴和偏航轴信号，而LQR 控制相比之下效果更好。从图9 和图10 可以看出，俯仰轴响应速度更快，信号延迟得到改善，虽仍存在一定的稳态误差，可能是建模时未考虑库伦摩擦，但基本能跟踪期望轨迹。偏航轴的运动跟踪控制虽存在一定延迟，但几乎没有误差，经过多次反复实验，其跟踪性能良好，基本可以满足设计要求。

综上所述，采用LQR 控制方法所取得的效果良好，基本可以满足该系统的跟踪控制要求。

4 结语

研究二自由度直升机姿态控制策略，往往存在解决强耦合的难点，采用传统PID 控制对于单一姿态角具有较好的控制效果，而在同时控制两个姿态角的过程中表现出较差的跟踪控制能力。为满足二自由度直升机系统的性能要求，本文研究了LQR 控制方法，设计出一种状态反馈控制器，建立了二自由度直升机的动力学模型，确定了最优控制规律，并利用LabVIEW 构建软件平台，最终实现了对俯仰角度和偏航角度的实时跟踪。仿真实验结果表明，LQR 控制克服了传统PID 控制的缺陷，同时跟踪控制两个姿态角的效果良好，能够基本达到系统的运行目标，有效解决了系统的耦合性。