具有故障边的二维环面网络的哈密尔顿路
2021-12-31张建秀田小润
张建秀,李 晶,田小润
(太原科技大学 应用科学学院,太原030024)
随着当前信息量的日益增加,在太空、国防、科技等各个领域已经出现了大量具有挑战性的应用问题,因此大规模并行计算机系统应用而生,为大规模并行计算机系统设计更高效更可靠的互连网络成为网络设计者们不断追求的目标。环面网络作为大规模并行计算机的互连网络,近年来受到广泛关注[1]。
哈密尔顿圈和路的存在问题是互连网络研究中的经典问题。关于二维环面网络(即Torus网络)的哈密尔顿性质,学者们已经得到很多相关成果:设F是Torus网络中的故障集合,Kim和Park在2000年证明了当F是故障点集且|F|≤1时,Torus(m,n),其中m,n≥4是偶数,是偶哈密尔顿连通的[2]。2003年,Park和Kim推广了这一结论,证明了当F是故障点集或边集且|F|≤1时,Torus(m,n),其中m,n≥4是偶数,是偶哈密尔顿蕾丝的[3]。 Xiang等人[4]证明了当F是故障边集且|F|≤3时,如果Torus(m,n)-F中没有1度点,Torus(m,n)(m,n≥3)是哈密尔顿的。2017年,Li等人将故障边集的数目再次提高,得到结论:当F是故障边集且|F|≤4时,如果Torus(m,n)-F中没有1度点也没有f4圈,则Torus(m,n)(m,n≥5)仍然是哈密尔顿的[5-6]。然而,在上面的研究中,随着故障边数的增加,学者们都假设Torus(m,n)-F中没有1度点,对存在1度点的情形,没有文献讨论此时网络中哈密尔顿圈和路的存在问题。本文将对这一情形进行详细地讨论。
1 预备知识
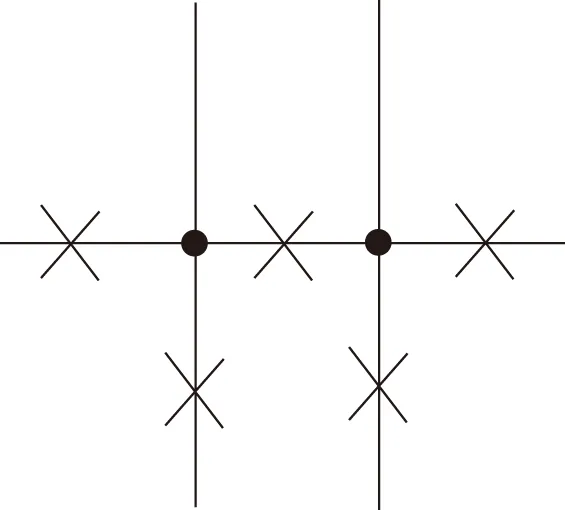
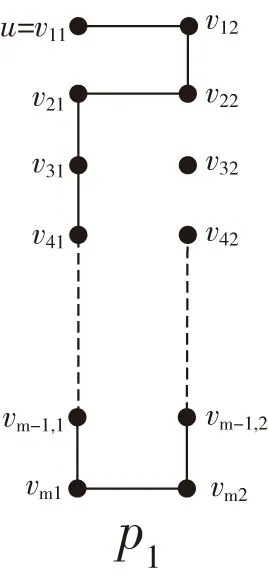
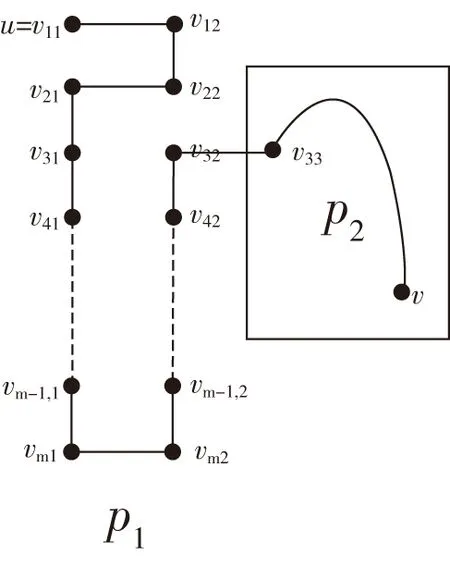
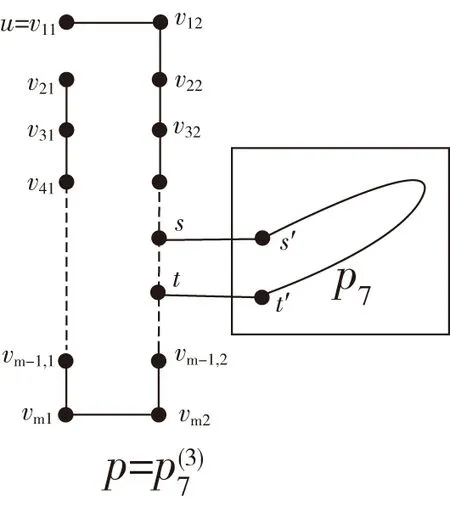
一个二维m×n环面(简记为Torus(m,n),其中m,n均为偶数)的顶点集为V={vij|1≤i≤m,1≤j≤n},边集为E={Er∪Ec},其Er={(vij,vi,j+1)|1≤i≤m,1≤j 图1 Torus(4,6)Fig.1 Torus(4,6) 图2 Row-Torus(4,6)和Gird-Torus(4,6)Fig.2 Row-Torus(4,6)and Gird-Torus(4,6) 令G=Torus(m,n),定义R(i)与C(j)分别为第i行、第j列的点导出的G的子图,即R(i)=G〈{vij|1≤j≤n}〉、C(j)=G〈{vij|1≤i≤m}〉.令R(i:i′)=G〈{vkj|i≤k≤i',1≤j≤n}〉,否则R(i,i′)=∅.同样地,令C(j:j′)=G〈{vik|1≤i≤m,j≤k≤j′}〉,否则C(j,j')=∅.包含Torus(m,n)的每个顶点的路称为Torus(m,n)的Hamilton路;类似地,Torus(m,n)的Hamilton圈是指包含Torus(m,n)的每一个顶点的圈。 定义F为G中故障点集或故障边集。当F⊂V(G)且|F|≤f时,如果对于G-F中每一对顶点v和w,都有一条从v到w的哈密尔顿路,则称图G是f-点故障哈密尔顿连通的。当F⊂E(G)且|F|≤f时,如果对于G-F中每一对顶点v和w,都有一条从v到w的哈密尔顿路,则称图G是f-边故障哈密尔顿连通。类似地,当F⊂V(G)且|F|≤f时,G-F中有哈密尔顿圈,则称图G是f-点故障哈密尔顿圈的。当F⊂E(G)且|F|≤f时,G-F中有哈密尔顿圈,则称图G是f-边故障哈密尔顿圈的。 当m,n均为偶数时,Torus(m,n)是二部图。因此定义若i+j为偶数则称vij为偶点,若i+j为奇数则称vij为奇点。 具有二部集合X和Y的二部图G是偶哈密尔顿连通的,如果满足下列条件之一:(1)若|X|=|Y|,则对于任意的v∈X,w∈Y,都存在从v到w的哈密尔顿路;(2)若|X|=|Y|+1,则对于任意的v,w∈X,都存在从v到w的哈密尔顿路。 f4圈是指存在一对不相邻顶点u、w均为2度点的4圈(u,v,w,x). 下面给出一些Torus以及Row-Torus的一些性质,这些性质将在证明中用到。 引理1[2]Torus(m,n),其中m,n≥4是偶数,是1-点故障-偶哈密尔顿连通的。 引理2[3]Row-Torus(m,n),其中m≥2,n≥4是偶数,是1-边故障-偶哈密尔顿连通。 引理3[5]在Torus(m,n)中,m,n≥5,故障边集|F|≤4.若Torus(m,n)-F中没有1度点也没有f4圈,则Torus(m,n)-F中有哈密尔顿圈。 定理1在Torus(m,n)中,m,n≥4是偶数,F是故障边集且|F|≤4,u为Torus(m,n)-F中的唯一1度顶点。对任意的v,若v与u奇偶性不同且(u,v)∉E(Torus(m,n)-F),则Torus(m,n)-F中存在哈密尔顿路连接u和v. 证明:不失一般性,设u=v11,v12是v11的邻点且(v11,v12)∉F.容易知道u是偶点,v是奇点。因为在Torus(m,n)中每点的度均为4,点u为Torus(m,n)-F中的1度点,因此有3条故障边与u关联,|F|≥3. 情形1当|F|=3时,G=Torus(m,n)-u中无故障边,由引理1,G=Torus(m,n)-u是1-点故障-偶哈密尔顿连通的。由于v12与v均为奇点,所以点v12与v之间有G的一条哈密尔顿路P.此时 情形2当|F|=4时,与u不关联的故障边记为f.在C(1:2)中构造一条路P1= 图3 情形2Fig.3 Case 2 情形2.1v∈V(C(3:n))且f∉E(P1)∪{(v32,v33)} 容易观察到,C(3:n)与Row-Torus(n-2,m)同构。因为n-2≥2,m≥4是偶数,由引理2,C(3:n)是1-边故障-偶哈密尔顿连通的。由v33是偶点、v是奇点,则C(3:n)中存在从v33到v的哈密尔顿路P2.此时 图4 情形2.1Fig.4 Case 2.1 情形2.2v∈V(C(3:n))且f∈E(P1)∪{(v32,v33)} 图5 情形2.2Fig.5 Case 2.2 情形2.3v∈V(C(1:2)∩R(3:m)) 在R(1:2)中构造一条路P4= 图6 情形2.3Fig.6 Case 2.3 情形2.3.1f∉E(P4)∪{(v23,v33)} 容易观察到,R(3:m)与Row-Torus(m-2,n)同构。因为m-2≥2,n≥4是偶数,由引理2,R(3:m)是1-边故障-偶哈密尔顿连通的。由v33是偶点、v是奇点,则R(3:m)中存在从v33到v的哈密尔顿路P5.此时 图7 情形2.3.1Fig.7 Case 2.3.1 情形2.3.2f∈E(P4)∪{(v23,v33)} 图8 情形2.3.2Fig.8 Case 2.3.2 情形2.4v∈V(C(1:2)∩R(1:2)) 情形2.4.1f∉E(P1) 图9 情形2.4.1Fig.9 Case 2.4.1 情形2.4.2f∈E(P1) 图10 情形2.4.2Fig.10 Case 2.4.2 定理2在二维环网Torus(m,n)中,m,n≥6是偶数,F是故障边集且|F|≤5.若Torus(m,n)-F有唯一一个1度顶点u,其余顶点至少为2度点。则点u至少有两个邻点与u之间有哈密尔顿路且这些邻点与u以故障边连接。 证明:u为1度顶点,所以与u关联的故障边有3条。设(u,v)∈F. 当|F|≤4时,令F′=F 当|F|=5时,对u的邻点v,若(u,v)∈F,取F′=F 本文主要对二维环网中出现一个1度点的情况下的哈密尔顿路的存在问题进行了仔细的刻画和讨论。本文的结果可以看作前人研究结果的补充。 值得指出的是,定理1中故障边的数目|F|≤4不能改进。因为若|F|=5,此时可能出现两个1度顶点。如图11所示。 图11 具有5条故障边的可能情形Fig.11 A possible case with 5 fault edges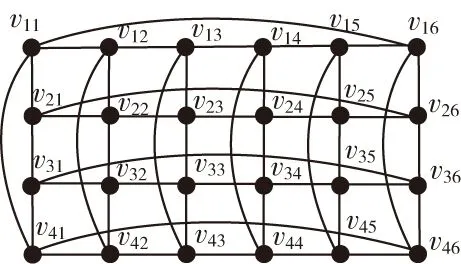

2 主要结果的证明
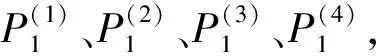
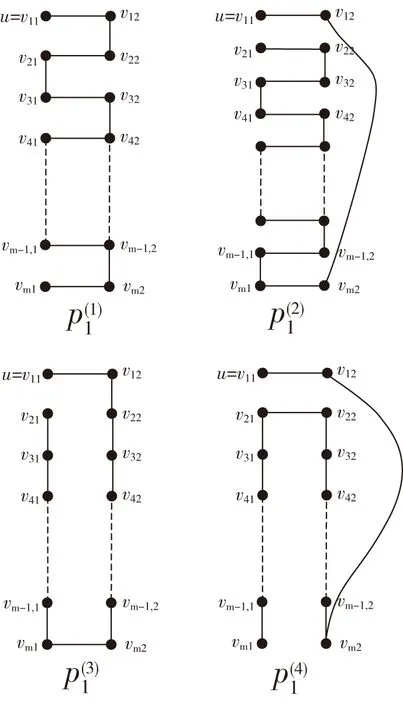

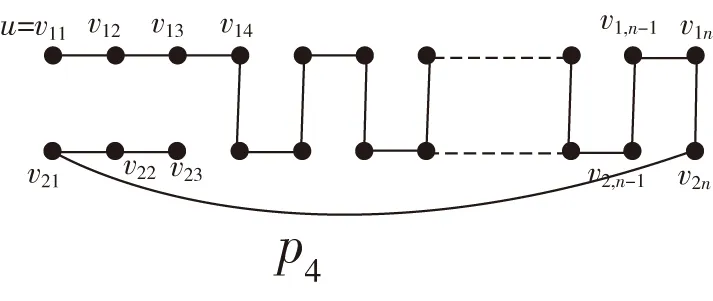
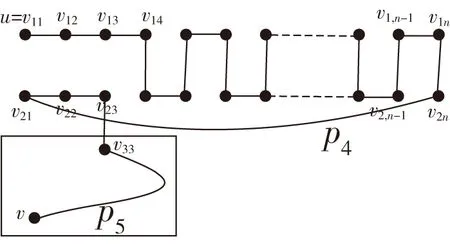



3 结论