预紧力与结构参数对角接触球轴承寿命的影响
2021-12-31肖志刚赵春江张雨田刘冰洋
肖志刚,赵春江,曾 光,张雨田,刘冰洋
(太原科技大学 重型机械教育部工程研究中心,太原 030024)
高速角接触球轴承是航空航天、高速机床等装配制造业中的关键性零部件,其动态特性参数直接影响设备的运转性能。由于表面循环接触应力的影响,接触疲劳成为滚动轴承主要的破坏形式。预紧力是影响角接触球轴承刚度及疲劳寿命的一个重要因素,施加合适的预紧力可以提高轴承刚度,消除因高速滚动体离心力和陀螺力矩造成的滚动体陀螺滑动,防止摩擦、磨损和温升的急剧增加,延长轴承的疲劳寿命[1-6]。
多年来,国内外学者对高速角接触球轴承性能的研究已取得了很多研究成果。Yan等提出了次表面应力和疲劳寿命的预测方法,基于润滑油非牛顿特性,建立了同时考虑自旋和润滑油非牛顿特性的点接触热弹流润滑模型。唐云冰等建立了在轴向力、离心力、径向力及陀螺力矩耦合影响下的滚动轴承分析模型,研究了不同结构和工况参数对轴承力学特性的影响。Zhang等建立了分析高速球轴承的球-滚道接触状态的力学模型,基于外载荷、转速及预紧力对球-滚道接触状态的影响,给出了预紧力和轴承寿命的关系[7-11]。
本文采用拟静力学分析方法对受径向和轴向联合负荷的高速角接触球轴承进行了求解计算,基于求解结果,根据Lundberg-Palmgren疲劳寿命理论,进行了疲劳寿命计算,同时计算了摩擦力矩,最后分析了预紧力和结构参数同时变化对高速角接触球轴承所受摩擦力矩和疲劳寿命的影响规律,为高速角接触球轴承的结构设计和使用提供理论依据。
1 角接触球轴承拟静力学模型
1.1 角接触球轴承变形协调方程
图1表示任意位置第j个滚动体球心与内、外沟曲率中心的相对位置图。B表示外沟曲率中心位置,固定不动,A、A′分别表示受载前后的内沟曲率中心位置,O、O′分别表示受载前后的滚动体球心位置。
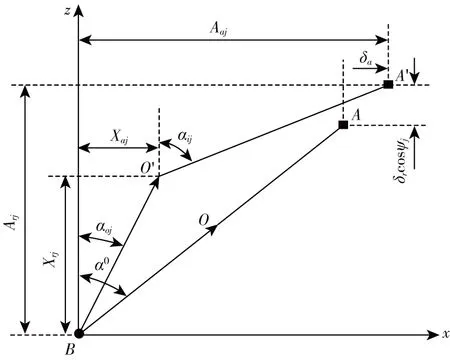
图1 曲率中心的相对位置Fig.1 Relative position of curvature center
由图1所示几何关系,可得变形协调方程:
(Aaj-Xaj)2+(Arj-Xrj)2-
[(fi-0.5)Dw+δij]2=0
(1)
(2)
式中:Xaj、Xrj为受载后球心位置的坐标值,Aaj、Arj为受载后内沟曲率中心位置的坐标值,δij、δoj分别为滚动体与内、外滚道的接触变形,fi、fo分别为内、外沟曲率半径系数。
1.2 接触角方程
受离心力作用的影响,受载后,滚动体与滚道的接触角发生改变,第j个球位置处滚动体与内、外滚道的接触角:
(3)
(4)
(5)
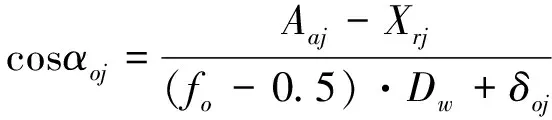
(6)
1.3 接触变形与载荷的关系
根据赫兹接触理论,滚动体与内、外圈的接触负荷为:
(7)
(8)
式中:Kij、Koj分别为滚动体与内外滚道的接触—变形常数。
1.4 滚动体受力平衡方程
Qij·sinαij-Qoj·sinαoj-Fxij·cosαij+
Fxoj·cosαoj=0
(9)
Qij·cosαij-Qoj·cosαoj+Fxij·sinαij-Fxoj·sinαoj+Fcj=0
(10)
式中:Qij、Qoj分别为滚动体与内、外滚道之间的接触载荷;Fxij、Fxoj分别为滚动体与内、外滚道间的摩擦力;Fcj为滚动体所受离心力;Mgj为陀螺力矩。
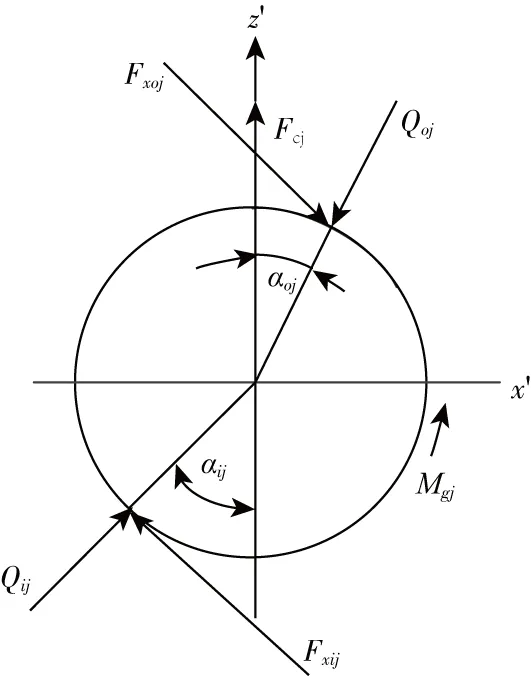
图2 滚动体受力图Fig.2 Load on the ball
1.5 套圈平衡方程
由内圈在轴向力和径向力作用下的平衡关系,可得内圈平衡方程:
(11)
(12)
式中:Fa、Fr分别为轴承所受轴向载荷和径向载荷;ψj为滚动体方位角。
2 角接触球轴承疲劳寿命计算
在法向载荷Q作用下,角接触球轴承的接触疲劳寿命由下式计算:
(13)
式中:L10为90%可靠度的轴承基本额定寿命,单位为106转;Qc为滚动体额定动载荷;Q为滚动体所受的接触载荷。
用Li与Lo分别表示轴承内、外圈的疲劳寿命,则:
(14)
(15)
式中:Qci、Qco分别表示内、外圈滚动体的额定动载荷;Qi、Qo分别表示内、外圈滚动体的实际接触载荷。
内、外圈滚动体的额定动载荷分别如下:
(16)
(17)
式中:dm表示轴承节圆直径,γi=Dwcosαi/dm,γo=Dwcosαo/dm,αi、αo分别表示实际内、外接触角,Dw表示滚动体直径,Z表示滚动体个数。
根据乘积定律将旋转和非旋转滚道的寿命进行统计处理,可得到角接触球轴承的整体寿命:
(18)
在轴承转速一定条件下,为了表达方便,可用旋转时间Lh来表达寿命:
Lh=106L/60n
(19)
式中:n表示轴承转速,单位为r/min.
3 摩擦力矩
滚动轴承中存在着极其复杂的摩擦现象,在轴承实际应用中轴承的摩擦特性是不容忽视的。轴承的摩擦力矩指由各种摩擦因素产生的阻碍轴承运转的阻力矩[12]。
M=M0+M1
(20)
式中:M0为与轴承类型、转速和润滑剂有关的摩擦力矩,M1为与轴承外载有关的摩擦力矩。
M0=10-7f0(vn)2/3dm3
(21)
式中:dm为轴承节圆直径,f0为与轴承类型和润滑方式有关的系数,n为轴承转速,v为工作温度下润滑剂的运动粘度。
M1=f1P1dm
(22)
式中:f1为与轴承类型和外载有关的系数,P1为确定轴承摩擦力矩的计算负荷。
4 计算结果与分析
为了验证上述理论,本文算例采用218ACBB角接触球轴承,其基本结构参数如表1所示,滚动体材料采用陶瓷,内外套圈材料采用轴承钢,润滑采用4109合成润滑油,工作温度为40 ℃,轴承内圈转速为10 000 r/min,外圈固定,径向力大小为2 000 N.采用Newton-Rsaphson迭代法,联立式(1)-式(12)对拟静力学计算模型进行求解计算。基于该算例,通过疲劳寿命计算模型分析预紧力和轴承各结构参数联合变化对轴承所受摩擦力矩、疲劳寿命等方面的影响。
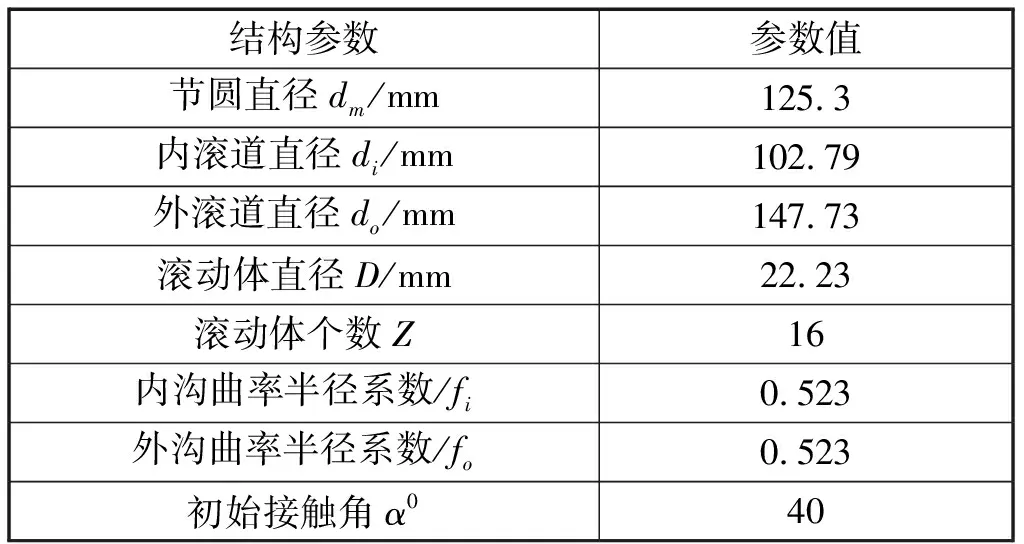
表1 角接触球轴承基本结构参数
在预紧力分别与滚动体直径、滚动体个数、初始接触角一起变化时,摩擦力矩及疲劳寿命的计算结果分别如图3至图8所示。
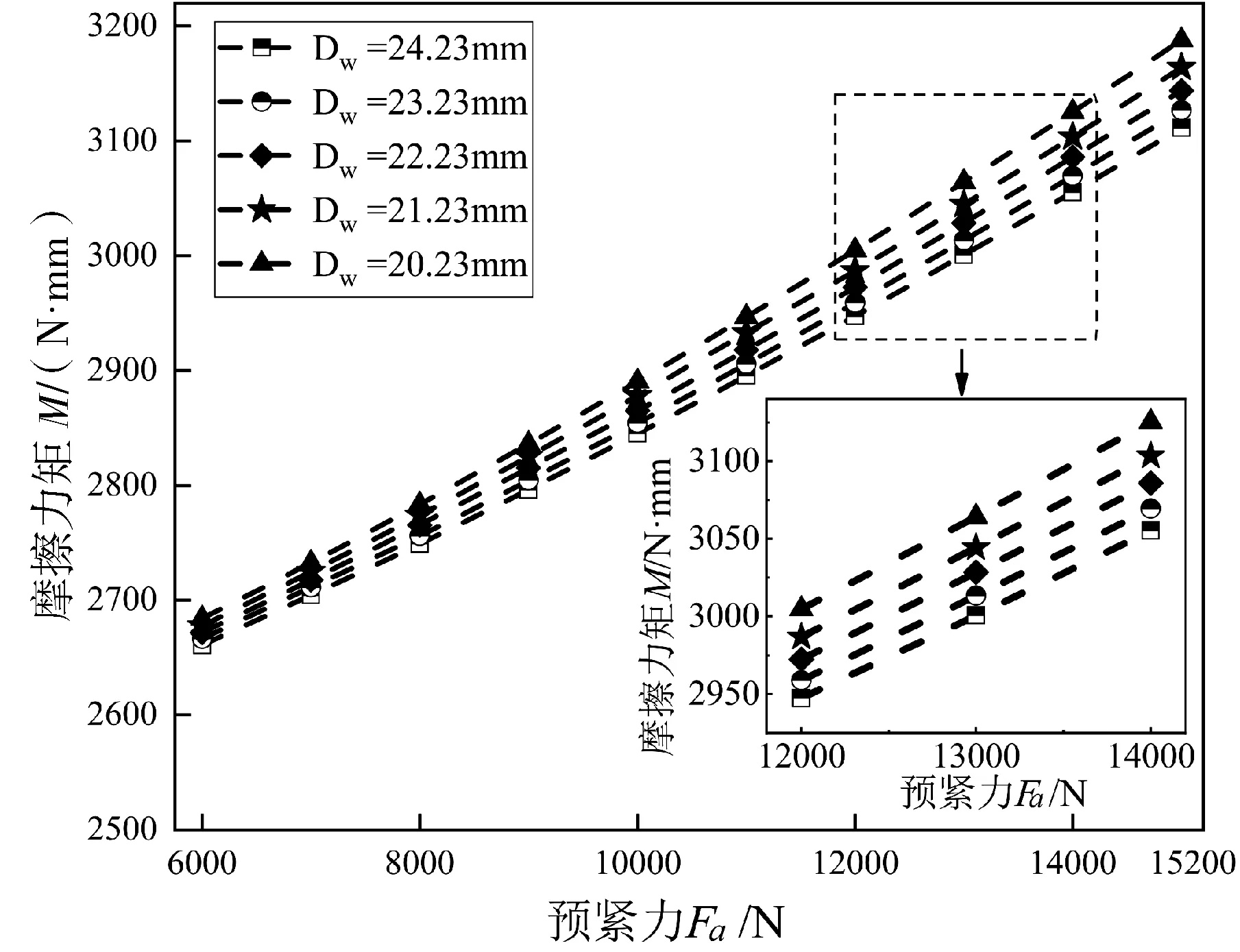
图3 预紧力和滚动体直径对摩擦力矩的影响Fig.3 The influence of preload force and roller diameter on friction torque
由图3和图4可知,相同滚动体直径下,轴承所受摩擦力矩随着预紧力的增大而增大,轴承总体寿命逐渐减小,Dw=24.23 mm时,轴承所受最大摩擦力矩值与最小值的差值为451 N·mm,最大轴承寿命值与最小值的差值为2 824 h,Dw=20.23 mm时,轴承所受最大摩擦力矩值与最小值的差值为500 N·mm,最大轴承寿命值与最小值的差值为1 163 h;相同预紧力下,轴承所受摩擦力矩,随着滚动体直径的增大而减小,轴承总体寿命逐渐增加,Fa=6 000 N时,轴承所受最大摩擦力矩值与最小值的差值为24 N·mm,最大轴承寿命值与最小值的差值为3 257 h,Fa=15 000 N时,轴承所受最大摩擦力矩值与最小值的差值为76 N·mm,最大轴承寿命值与最小值的差值为935 h.说明适当减小预紧力和增大滚动体直径可以减小摩擦力矩,使轴承总体寿命增加。
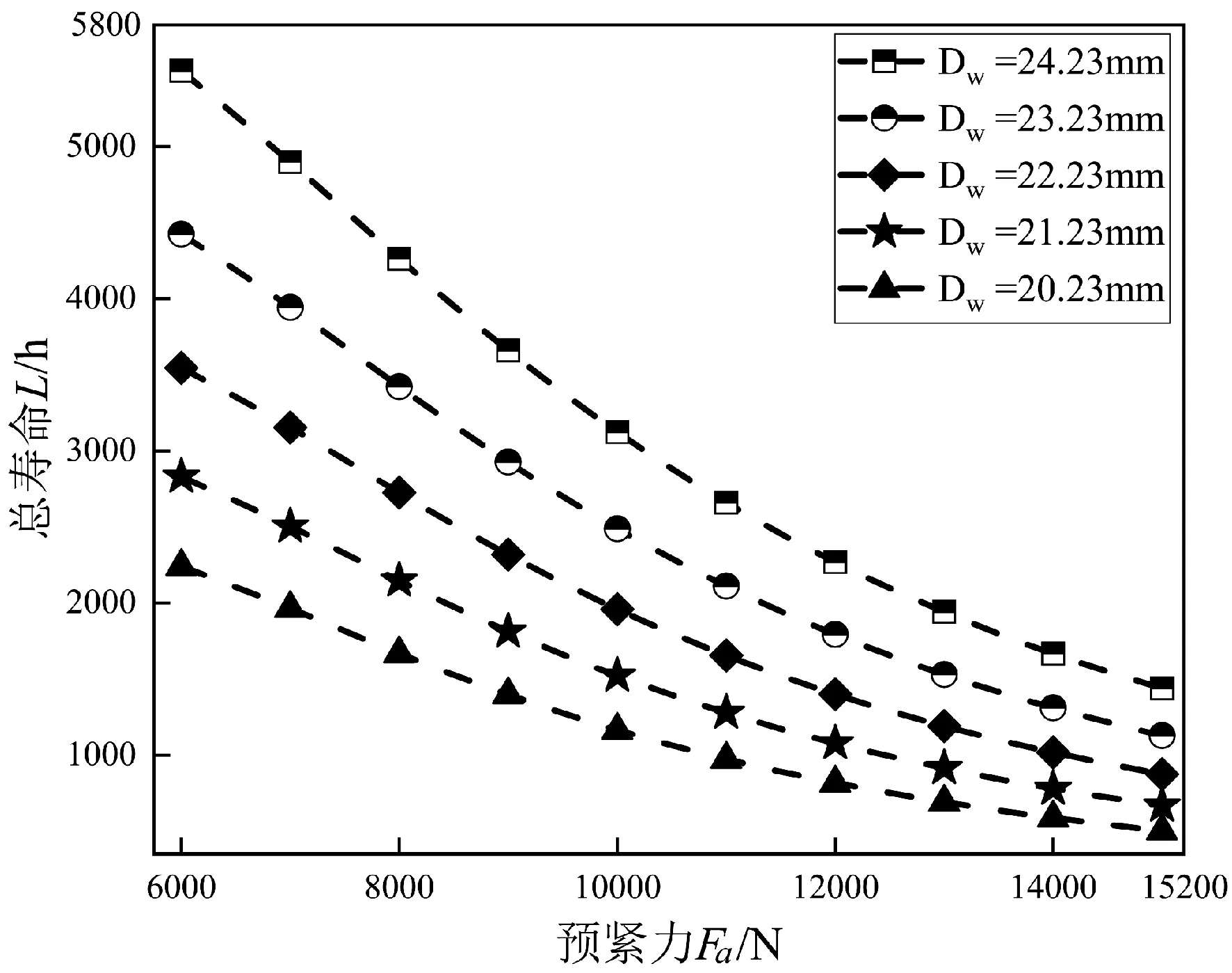
图4 预紧力和滚动体直径对轴承总体寿命的影响Fig.4 The influence of preload force and roller diameter on the overall life of bearing
由图5和图6可知,相同滚动体个数下,轴承所受摩擦力矩随着预紧力的增大而增大,轴承总体寿命逐渐减小,Z=18时,轴承所受最大摩擦力矩值与最小值的差值为454 N·mm,最大轴承寿命值与最小值的差值为3 150 h,Z=14时,轴承所受最大摩擦力矩值与最小值的差值为495 N·mm,最大轴承寿命值与最小值的差值为2 077 h;相同预紧力下,轴承所受摩擦力矩随着滚动体个数的增加而减小,轴承总体寿命逐渐增加,Fa=6 000 N时,轴承所受最大摩擦力矩值与最小值的差值为18 N·mm,最大轴承寿命值与最小值的差值为1 526 h,Fa=15 000 N时,轴承所受最大摩擦力矩值与最小值的差值为59 N·mm,最大轴承寿命值与最小值的差值为453 h.说明适当减小预紧力和增加滚动体个数可以减小摩擦力矩使轴承总体寿命增加。
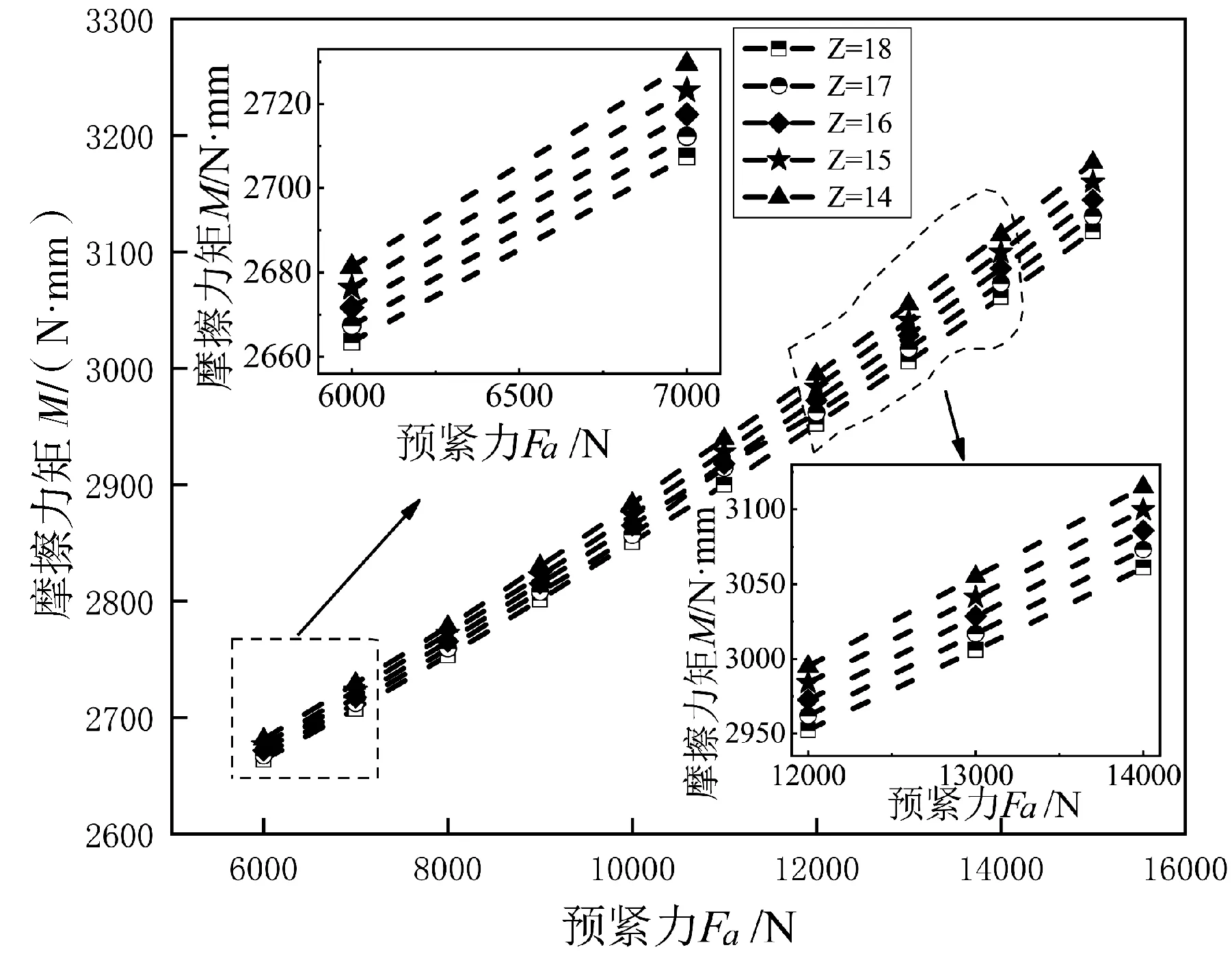
图5 预紧力和滚动体个数对摩擦力矩的影响Fig.5 The influence of preload force and number of rolling body on friction torque
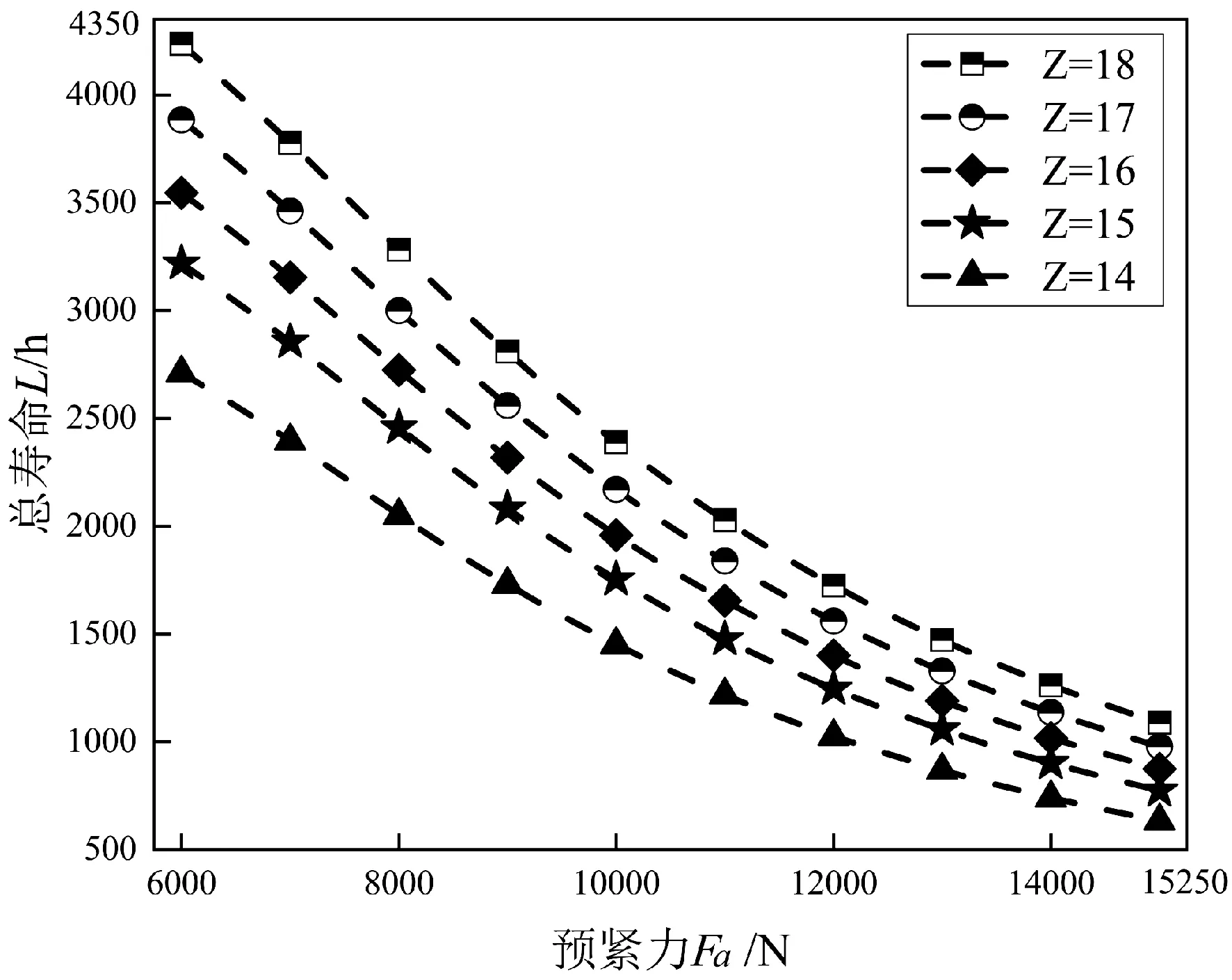
图6 预紧力和滚动体个数对轴承总体寿命的影响Fig.6 The influence of preload force and number of rolling body on the overall life of bearing
由图7和图8可知,相同初始接触角下,轴承所受摩擦力矩随着预紧力的增大而增大,轴承总体寿命逐渐减小,α0=42°时,轴承所受最大摩擦力矩值与最小值的差值为477 N·mm,最大轴承寿命值与最小值的差值为2 469 h,α0=38°时,轴承所受最大摩擦力矩值与最小值的差值为469 h,最大轴承寿命值与最小值的差值为2 947 h;相同预紧力下,轴承所受摩擦力矩随着初始接触角的增大几乎不发生变化,轴承总体寿命在预紧力小于9 000 N时,随着初始接触角的增大而减小,预紧力大于9 000 N时,随着初始接触角的增大而增大,Fa=6 000 N时,轴承所受最大摩擦力矩值与最小值的差值为1 N·mm,最大轴承寿命值与最小值的差值为342 h,Fa=9 000 N时,轴承所受最大摩擦力矩值与最小值的差值为2 N·mm,最大轴承寿命值与最小值的差值为8 h,Fa=15 000N时,轴承所受最大摩擦力矩值与最小值的差值为9 N·m,最大轴承寿命值与最小值的差值为73 h.说明在选取最佳预紧力时初始接触角对轴承摩擦力矩和总体疲劳寿命的影响可不必考虑。
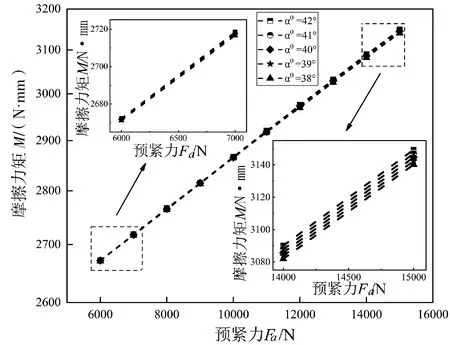
图7 预紧力和初始接触角对摩擦力矩的影响Fig.7 The influence of preload force and initial contact angle on friction torque
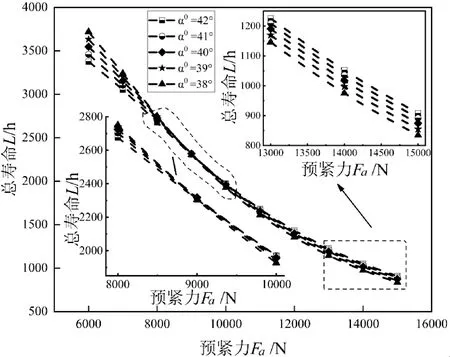
图8 预紧力和初始接触角对轴承总体寿命的影响Fig.8 The influence of preload force and initial contact angle on the overall life of bearing
5 结论
(1)当轴承转速和径向力一定时,在预紧力分别和滚动体直径、滚动体个数及初始接触角联合变化下,总体上,轴承摩擦力矩随预紧力的增大而急剧增大,导致轴承寿命急剧减小。
(2)增大滚动体直径和增加滚动体个数可以减小轴承摩擦力矩,延长轴承寿命,但影响幅度小于预紧力的影响;初始接触角的变化对轴承摩擦力矩和疲劳寿命带来的影响很小,选取预紧力时可以不考虑初始接触角对轴承摩擦力矩和疲劳寿命的影响。
(3)摩擦力矩对轴承疲劳寿命的影响非常明显,在进行轴承优化延长寿命时,应该将摩擦力矩作为重要的考虑因素。
