冻结黏土的强度与变形特性及参数研究

陈雨漫，林 斌

(安徽理工大学土木建筑学院，安徽 淮南 232001)

现如今人工冻结法在土木工程领域得到广泛应用，其中冻土强度与变形特性是保证工程安全进行的重要因素，因此研究土体在冻结状态下的强度与变形特性具有重要的意义。

人工冻土强度值受到土质类型、冻结温度、含水率等因素的共同影响。文献[6]对粉质黏土地层进行水泥改良后再进行冻结,通过室内实验获得水泥改良后粉质黏土冻结强度的变化规律强度。文献[7-8]通过进行不同温度、含水率、加载速率的冻土单轴抗压强度试验，得到冻土单轴抗压强度受温度、含水率等因素影响的变化规律，并建立了考虑温度、含水率等因素的强度模型。文献[9-10]研究了温度对原状土、重塑土强度的影响，分析了不同温度及不同深度下土体压缩的变化规律。文献[11-13]研究了围压对三轴强度的影响，试样应力-应变关系曲线可分为软化型和硬化型，围压较小时为软化型，反之为硬化型。目前，人工冻结细粒土如黏土、粉质黏土及粉土等单轴或三轴剪切强度研究较为广泛。通过研究发现，人工冻结粉土、黏土以及粉黏土等的抗剪强度均随冻结温度的降低而增大。

目前对冻土的单轴抗压强度与三轴强度有了一定的研究，但是对冻土在单轴和三轴受压状态下强度与变形特性及相关参数间联系的研究不够深入，而研究土体在冻结状态下的强度与变形特性是冻结壁设计的关键。为此本文以煤矿冻结法施工中较为常见的黏土为研究对象，通过进行冻土单轴抗压强度试验和冻土三轴强度试验，探索冻土在单轴受压和三轴受压时的强度与变形特性及相关参数，以及冻土单轴抗压强度与三轴剪切强度之间的联系，以期为矿井冻结施工中冻结参数的选取提供一定的参考。

1 试样的参数及试验方法

1.1 试样的参数

研究选用某矿地下158.8～178.9m的原状黏土，土样的含水率为27.74%,湿密度为2.015g/cm。

1.2 试验方法

冻土单轴抗压强度试验在WDT-100冻土性能试验机中进行， 试验机配备的有低温环境箱， 温度波动范围误差控制在0.1℃。 在试验之前， 将土样制成直径50mm、 高100mm的圆柱体试样，要求端面修理平整，选取3个不同点进行量测，取其平均值保证直径误差不超过1mm，两端面长度误差不超过0.5mm。将试样分为3组，分别在-5℃、-10℃、-15℃条件下恒温24h后取出放入试验机中，试验按应变控制加载方式进行，应变速率控制在1%/min，试验数据由计算机根据设定好的参数自动控制和采集。

冻土三轴剪切试验在W3Z-200型三轴试验机中进行， 试验机由低温箱、 自动加载系统、 数据采集仪等组成。 试验过程中的加载、 数据采集及试验结束全由计算机自动控制。 试样尺寸为直径61.8mm、高度125mm的圆柱体，采用标准制样方法制备土样。 确定试验温度为-5℃、 -10℃和-15℃三个温度水平，对同一组试样分3种不同的围压(2MPa、3MPa、4MPa)进行剪切试验，三轴剪切强度试验按轴向应变速率0.08%/min进行剪切加载，对试样先进行固结、后冻结，达到设计温度后，恒温不少于24h再进行剪切试验。

2 试验结果

2.1 冻土单轴抗压强度

1)应力-应变关系

在不同温度水平下冻土的轴向应力-应变关系曲线如图1所示。-5℃、-10℃、-15℃冻土的应力-应变曲线均呈现出线性关系(在应变开始阶段)，随着应变的增加，应力增加速度开始逐渐减缓，当应力达到峰值强度以后，应变继续增加时，应力开始下降，这种应力-应变关系属于应变软化型。

图1 不同温度下的应力-应变曲线

2)温度对单轴抗压强度和峰值应变的影响

本研究把不同温度下冻土应力应变曲线的峰值强度作为冻土的单轴抗压强度，与单轴抗压强度对应的应变定义为峰值应变。不同温度下冻土的单轴抗压强度关系曲线如图2所示。

图2 单轴抗压强度与温度关系曲线

对图2中试验数据进行线性拟合得到其关系式为

σ

=-0

.

368

T

-0

.

086 7,

R

=0

.

981 3

(1)

式中：

σ

为单轴抗压强度，MPa；

T

为温度,℃。

随着温度的降低，冻土单轴抗压强度呈增加趋势。冻土强度主要取决于土颗粒与冰之间的胶结力，温度降低时，冰占含水总量的比例增大，提高了土颗粒与冰之间的胶结力，从而提高冻土的强度。

通过冻土不同温度下的应力-应变曲线可以看出三种负温下冻土的峰值应变在7%～13%。随着温度的降低，峰值应变呈现先增大后减小的趋势，温度降低导致土中未冻水含量减少，冰含量增加， 土的塑性增大。-10℃～-15℃内峰值应变呈减小趋势是由于由于试验所做试样有限，试验结果数据存在一定的离散性。

3)冻土的弹性模量

冻土弹性模量通常取冻土单轴抗压强度的一半与其所对应的应变值的比值，即

E

=(

σ

/

2)

/ε

12

(2)

式中：

E

为试样的弹性模量,MPa；

σ

为试样的单轴抗压强度,MPa；

ε

12为试样单轴抗压强度值的一半所对应的应变,%。

冻土在不同温度下的弹性模量及关系曲线如图3所示。对弹性模量与温度的关系进行线性回归分析得到拟合公式

图3 弹性模量与温度关系曲线

E

=-11

.

59

T

-12

.

666 7，

R

=0

.

850 7

(3)

式中：

E

为弹性模量,MPa；

T

为温度,℃。

可以看出冻土弹性模量与温度负相关，温度每下降1℃，弹性模量约增加11.59MPa。

2.2 冻土三轴抗剪强度

1)应力-应变曲线

图4为冻土在不同温度条件下的三轴应力-应变曲线。应变较小时，随着应变的增加，应力增加较快，在应变值较大时，应力增加较为缓慢。温度、围压对应力-应变曲线的形态均有影响，围压相同的情况下，随着温度的降低，冻土的抗剪强度呈增加趋势。

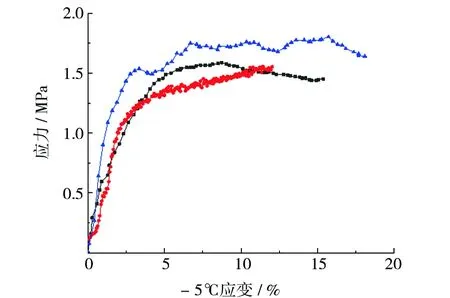
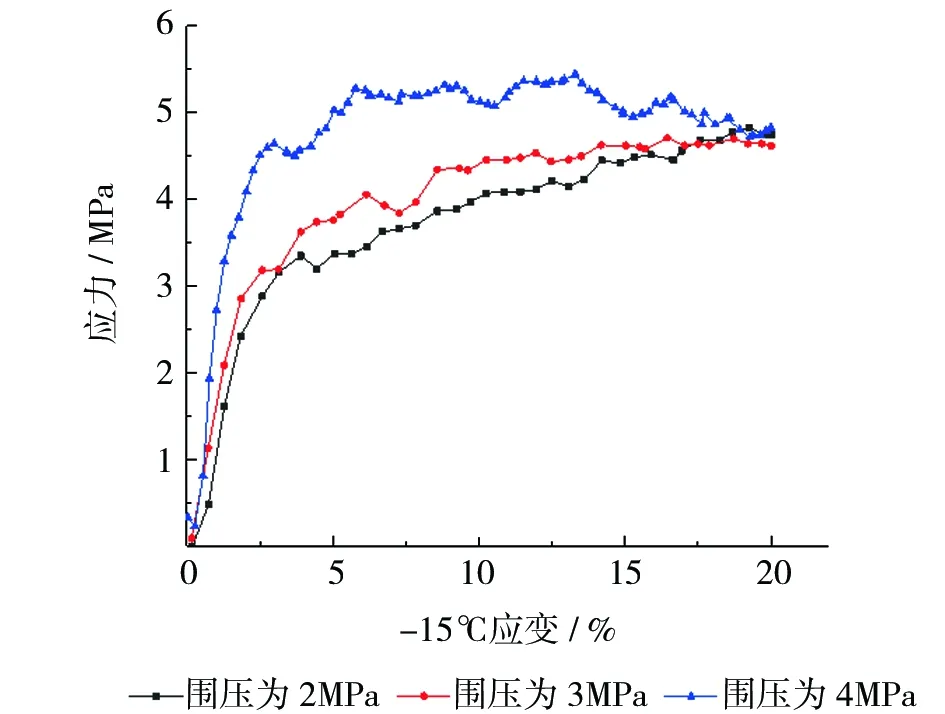
图4 不同温度下冻结黏土的应力-应变曲线

2)冻结黏土双曲线模型的建立

Kondner提出双曲线应力-应变模型,即

(4)

式中:

σ

为轴向应力，MPa；

σ

为围压,MPa；

ε

为轴向应变,%；

a

、

b

为试验常数。由于d

σ

=d

σ

，切线模量为

(5)

式中：

E

为切线模量,MPa。当应变较小时，

ε

=0,

E

=

E

，则初始弹性模量为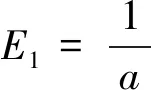

(6)

式中：

E

为初始弹性模量,MPa。

当应变趋于无穷大时，极限偏应力为

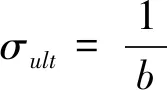
(7)

式中：

σ

为极限偏应力，MPa。经过计算，得到冻结黏土双曲线模型中参数

a

、

b

，初始弹性模量，极限强度，结果如表1所示。

表1 冻结黏土双曲线模型中参数值

在围压相同的情况下，随着温度的降低，参数

a

、

b

均呈减小趋势；初始弹性模量和极限偏应力均呈增加趋势。

3)参数变化规律及影响因素

为研究参数与温度和围压间的关系，对表1中的数据进行回归分析，得到回归方程为

a

=1

.

514 5-0

.

134 5

σ

+0

.

057 3

T

b

=0

.

722 0-0

.

001 2

σ

+0

.

036 0

T

(8)

式中:

a

、

b

均为试验常数；

σ

为围压,MPa；

T

为温度,℃。通过式(8)可以得到参数

a

、

b

与围压、温度的相关性相同，模型参数

a

、

b

均与围压呈负相关，与温度呈正相关。

将式(8)代入式(4)中，则

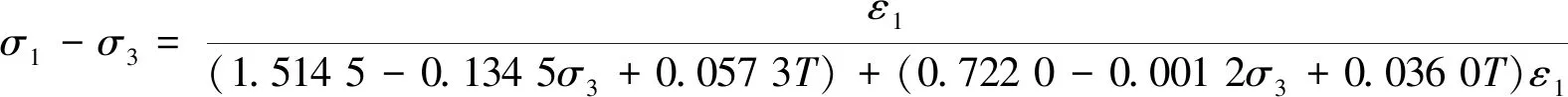
(9)

式中：

σ

为轴向应力,MPa；

σ

为围压,MPa；

ε

为轴向应变,%；

T

为温度,℃。冻土的抗剪强度随

σ

增加而增大，随温度降低而增大。围压增加使土颗粒之间更加紧密，增加了土体的整体性，从而抗剪强度得到提高。温度降低使冻土中未冻水含量减少，冰的胶结作用增强，从而使冻土的强度提高。

将式(8)代入式(6)、(7)可得：

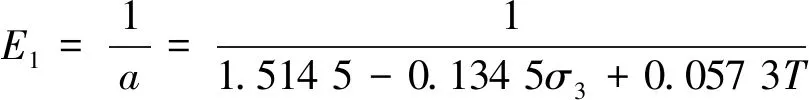
(10)

(11)

从式(11)可以得到初始弹性模量和极限偏应力均与围压呈正相关，与温度呈负相关。

根据试验结果，得到不同温度下冻结黏土的黏聚力和内摩擦角值，结果如表2所示。

表2 冻结黏土强度参数

通过线性拟合得到温度与冻土黏聚力的关系为

c

=-0

.

144

T

-0

.

057,

R

=0

.

993 6

(12)

式中：

c

为黏聚力,MPa；

T

为温度,℃。

随着温度降低，冻土的黏聚力呈增加趋势。温度每下降1℃，黏聚力约增加0.144MPa。温度的降低导致土中胶结冰的含量增加，土中冰胶结物的联结增强，冰和土体中固体颗粒胶结在一起共同承担冻土抗剪强度，因此表现为冻土的黏聚力随着温度的降低而增大。温度降低导致冰与土之间咬合力增加，提高了内摩擦角。由于试验所做样品有限，试验数据有离散性，内摩擦角虽然表现出先减后增，但总体上随温度降低呈增加趋势。

对于黏性土，根据线性M-C准则，可知

(13)

改写上式，可得

σ

-

σ

=

σ

sin

φ

+

σ

sin

φ

+2

c

cos

φ

(14)

(15)

单轴抗压强度是三轴压缩试验的一个特例，即周围压力

σ

=0的三轴试验。当

σ

为0时，由公式(15)得

(16)

式中:

c

为黏聚力，MPa；

φ

为内摩擦角,(°)；

σ

为轴向应力，MPa；

σ

为围压,MPa。

通过三轴试验得到的抗剪强度指标，推算单轴抗压强度理论值，进而与试验值进行对比，结果如表3所示。

表3 抗压强度对比分析

理论计算得到的单轴抗压强度与实际试验测得的单轴抗压强度关系如图5所示。通过图5可以看出两种方法得到的单轴抗压强度值均随温度的降低呈增加趋势，随着温度的降低，两种方法得到的结果之间的差值呈先减小后增加趋势。三种温度下两种方法测得的抗压强度相差数值均在1MPa以内，误差率在9%～31%。

两种方法得到的单轴抗压强度值存在偏差主要原因是在进行冻土三轴强度试验时对试样进行了固结，试验过程中有轴向荷载和围压共同作用，而进行单轴抗压试验时冻土只受到轴向荷载，且两种方式下加载速度不同，导致通过三轴试验得到的抗剪强度指标去推算单轴抗压强度理论值的结果存在一定的偏差。试验结果可为通过冻土三轴试验分析冻土单轴抗压强度提供一定的理论依据。

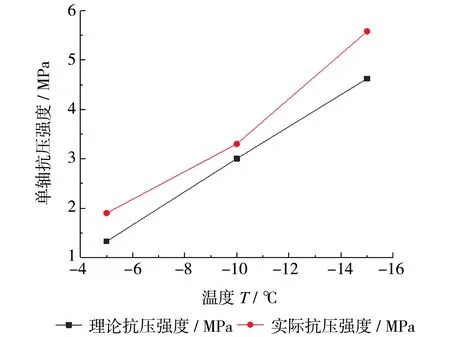
图5 理论值与试验值对比图

3 结论

(1)在试验温度下，冻土的单轴抗压强度和弹性模量均随温度降低而增加。

(2)冻土的初始弹性模量和极限偏应力均与围压呈正相关，与温度呈负相关。冻土的抗剪强度随围压增加而增大，随温度增加而减小。

(3)随着温度的降低，两种方法得到的单轴抗压强度之间的差值呈先减小后增加趋势。