多时间尺度下锂电池在线参数辨识及SOC估计

邢丽坤，郭 敏，张梦龙，詹明睿，凌六一,2

(1.安徽理工大学电气与信息工程学院，安徽 淮南 232001；2.安徽理工大学人工智能学院，安徽 淮南 232001)

电池管理系统的核心在于荷电状态(State of Charge，SOC)的准确估计， 当前研究SOC估算方法主要有阻抗法、 安时积分法、 开路电压法、 支持向量机(Support Vector Machines，SVM)、 神经网络法以及卡尔曼滤波法(Kalman Filter，KF)。阻抗法与开路电压法中电池需要长时间空载静置，不适用于动力电池SOC在线估计；安时积分法受到电池工作的过程噪声和仪器观测噪声影响，误差会随着时间推移而累积；神经网络法和SVM则受样本丰度和硬件限制，在实际运用中有一定的局限性。卡尔曼滤波算法，由于计算复杂度低、建模精确以及利用最优化自回归处理特性，在波动频繁、电流变化剧烈的动力电池中估算SOC具有很大的优势。非线性的卡尔曼滤波如扩展卡尔曼滤波算法(Extended Kalman Filter，EKF)、无迹卡尔曼滤波算法(Unscented Kalman Filter，UKF)算法或经人工智能算法改进的KF，目前在SOC估计上获得了广泛的使用，更适合锂电池SOC估计。

传统KF算法估计电池SOC时，需要建立离线电池模型，而离线模型的参数为固定值，会忽略电池参数在充放电过程中的变化，不能准确估计电池SOC。文献[7]利用单个EKF算法对SOC进行估算，但电池模型参数是通过离线辨识得到的，没有考虑电池参数会随着电池状态变化而变化。文献[8]提出双扩展卡尔曼滤波(Double Extended Kalman Filter，DEKF)算法在不同动态负载和电池健康状态(State of Health，SOH)阶段对SOC和电池参数进行估算；与简单的EKF算法相比，SOC估算精度有一定程度的提高，但DEKF算法也有缺点，这是因为非线性函数在

x

点处按泰勒级数展开，忽略了高阶项进而导致了一定的误差。锂电池进行模型参数辨识和SOC估算通常是在同一时间尺度下进行，可是在SOC估算中，时间尺度较小会导致处理器运算量大，同时考虑SOC是一个快速变化的量。因此众多文献开始提出不同时间尺度下电池参数和SOC估算的新方法。文献[11]提出了一种基于多时间尺度FFRLS-AEKF锂电池SOC估计方法，在保证SOC估算准确性的同时，减少了硬件的计算量，但该算法采用单一遗忘因子，不能随着电流变化快慢时刻改变。因此，上述方法均未能全面考虑电池参数时变性和硬件计算量等问题。

为了解决锂电池内部参数辨识和SOC估计不准确等问题，针对上述不同方法对电池SOC估计的优缺点，本文采用二阶RC等效电路模型，采用UKF算法对电池模型参数进行在线估算，将辨识出来的模型参数与EKF算法相结合对SOC进行多时间尺度估算，在(Urban Dynamometer Driving Schedule，UDDS)工况下，验证EKF-UKF联合算法的估算精度。

1 电池模型建立

电池模型是估算SOC的基础，由于Rint模型、一阶RC模型及PNGV模型在精确度方面有欠缺，综合考虑电池模型的复杂度和精度，采用二阶RC等效电路模型，如图1所示。

图1 二阶RC等效电路模型

其中

U

是电池的开路电压，

R

是电池的内阻，

R

、

C

用来描述双电层部分的荷电变化，主要是放电电压快速变化的过程，时间常数(

τ

=

R

C

)较小；

R

、

C

用来描述扩散现象，主要是放电电压缓慢稳定的过程，时间常数(

τ

=

R

C

)较大。

I

为端电流。

U

为

R

两端电压，

U

为

R

两端电压。根据模型结构，可推导模型状态方程如下

(1)

观测方程

U

=

U

(

SOC

)-

RI

-

U

-

U

(2)

式中：

C

、

C

为极化电容，F；

U

为端电压，V；

T

为采样时间(

T

=0

.

1s)；

Q

为电池容量，Ah；

R

、

R

为极化电阻，Ω。

2 实验

2.1 实验平台

本实验选用的单体电池是三元锂电池。电池尺寸是18mm×65mm，额定容量3Ah，充电截止电压4.2V，放电截止电压2.5V，电池电压3.6V，最大放电电流10A，最大充电电流1.5A。

实验平台如图2所示，主要由温控箱、数据采集卡、DC电源、电子负载、计算机控制系统构成。PC端通过串口对DC电源、电子负载发送指令，模拟锂电池工况条件，对电池进行充放电操作。采集卡用来获取电池的端电压、电流数据，将采集到的电流、电压数据实时传输到PC端。电子负载用于产生锂电池恒定电流或脉冲电流。温控箱用来控制锂电池实验时的环境温度。

图2 实验平台

2.2 OCV-SOC曲线实验

恒流放电实验得到锂电池不同SOC点处对应开路电压(OCV)值，通过多项式拟合得到锂电池OCV与SOC的函数关系。以10节并联三元锂电池为研究对象，首先将锂电池充满电，再用30A的恒流对锂电池进行放电，每次放0.1个SOC，即放电360s，放电结束后静置4h再进行下一次实验，重复10次即得到10个SOC点处对应的锂电池开路电压值。用八阶多项式拟合实验所测的数据，得到OCV-SOC拟合曲线，如图3所示。

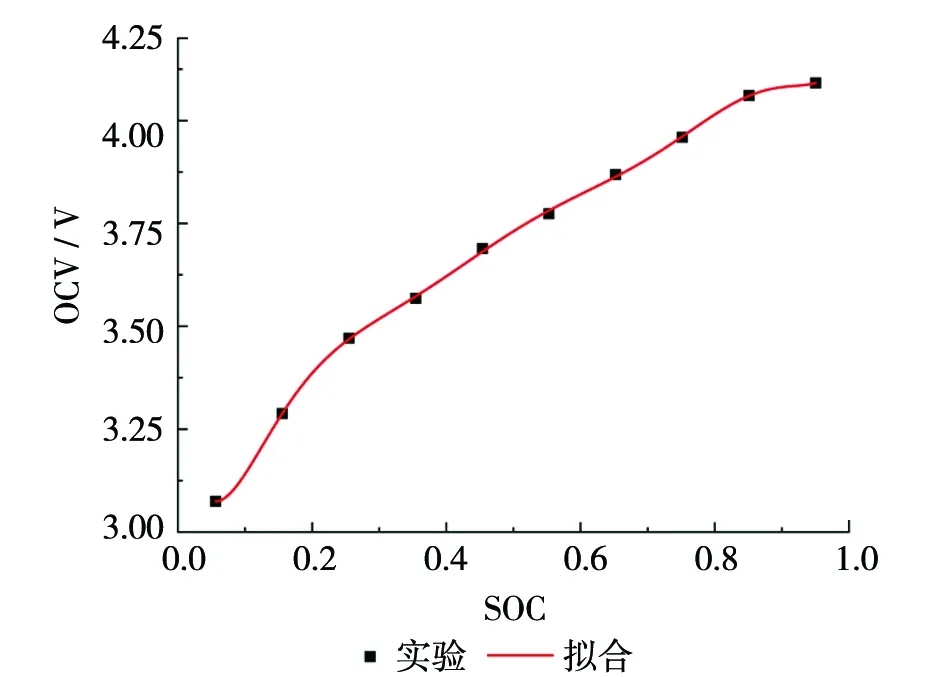
图3 OCV-SOC拟合曲线

拟合所采用的八阶多项式如式(3)所示，其各项系数如下所示

y

(

x

)=

p

x

+

p

x

+

p

x

+

p

x

+

p

x

+

p

x

+

p

x

+

p

x

+

p

(3)

其中

p

=117

.

46，

p

=-380

.

50，

p

=448

.

46，

p

=-202

.

42，

p

=-18

.

69，

p

=53

.

48，

p

=-21

.

80，

p

=5

.

34，

p

=2

.

82。

2.3 美国城市道路循环工况

在线参数辨识需要离线参数辨识中的混合动力脉冲能力特性实验获取参数初值，其后不再需要进行混合动力脉冲能力特性实验，可直接运用于实际工况中，以实际工况数据为基础结合算法实时辨识锂电池参数值。以UDDS工况作为实际工况，通过ADVISOR软件得到UDDS 下的工况电流，通过工况电流激励锂电池，从而得到UDDS工况下端电压。UDDS工况下电池电流和电压如图4所示。根据UDDS电流电压数据结合基于在线参数辨识的联合估计算法辨识出

R

、

R

、

C

、

R

、

C

，并实现SOC的估计。

图4 模拟UDDS工况下锂电池电流和电压波形

3 在线参数辨识与SOC联合估计

3.1 EKF-UKF的SOC估算策略

为实现电池模型参数和电池SOC的联合在线估计，采用UKF算法对电池模型参数

R

、

R

、

R

、

C

和

C

进行在线辨识，将辨识的参数值用于EKF状态估计。根据EKF算法估计SOC，通过OCV-SOC函数关系获得此刻的OCV，此时EKF算法在微观时间尺度下估计SOC。当微观时间尺度序列增大到宏观时间尺度时，UKF算法进行参数在线辨识；参数辨识结束后， EKF算法继续在微观时间尺度估计SOC。依次递推即可得到电池在不同时刻的模型参数和SOC估计值。多时间尺度下EKF-UKF联合算法结构如图5所示。

图5 多时间尺度EKF-UKF联合算法结构图

3.2 EKF-UKF联合算法

对式(1)进行离散化并联合式(2)，得到状态方程

(4)

锂电池的动态变化可通过式(4)表示，状态向量

x

=[

SOC

,

U

1,,

U

2,]，

U

通过OCV-SOC曲线获得。

U

与SOC成非线性关系，可用泰勒函数将

U

线性化成含SOC的函数式，因此使用泰勒公式将

U

,线性化变成带有

SOC

的表达式

(5)

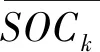
式(4)进一步简化可得到式(6)

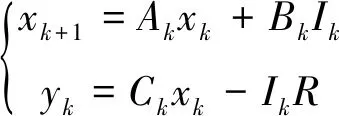
(6)

结合公式(4)～(6)，可得式(6)中输出矩阵

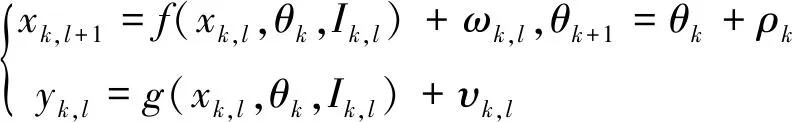
(7)

第一步：初始化状态变量

x

、状态变量误差协方差

P

,0、参数状态变量

θ

、参数状态变量误差协方差

P

初始化分别如下

x

=

E

(

x

)

(8)

(9)

θ

=

E

(

θ

)

(10)

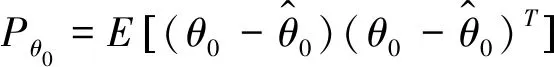
(11)

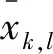
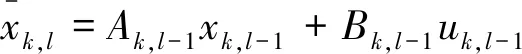
(12)

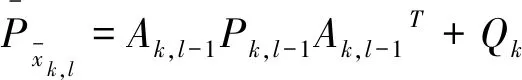
(13)

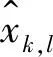
(14)

(15)

(16)

第三步：当SOC估计阶段达到宏观时间尺度即

l

=

L

时，将

l

置0，切换微观时间尺度到宏观时间尺度，采用无迹卡尔曼滤波算法进行一次参数辨识。首先计算宏观时间尺度下

k

时刻采样点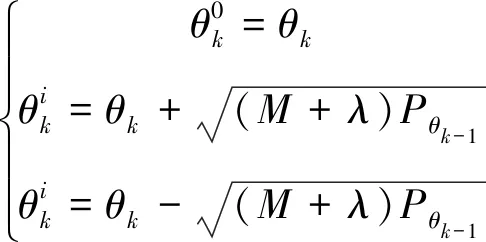

(17)

其中，

M

为状态向量的长度，本文中状态向量长度为5，权重值计算如下所示

(18)

其中，取

α

=0

.

01，

k

=0，

β

=2。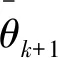

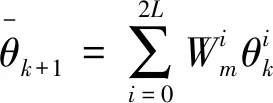
(19)

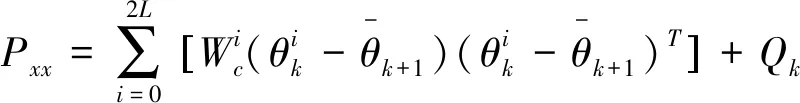
(20)

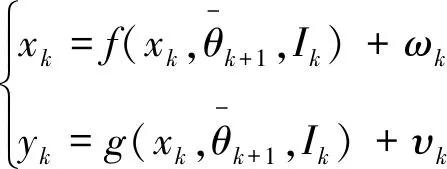
(21)

(22)

(23)

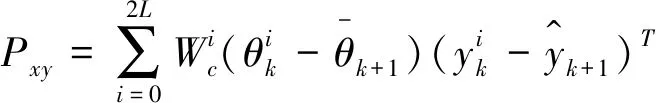
(24)

(25)

(26)

P

=

P

-

K

P

(27)

4 实验验证及分析

4.1 在线参数辨识结果分析

将UDDS工况数据导入EKF-UKF算法，在Matlab/Simulink中不断试验不同的宏观时间尺度和微观时间尺度，得到不同情况下SOC估计的平均绝对误差和均方根误差；通过比较平均绝对误差和均方根误差大小，最后分析得到当宏观时间尺度为60s和微观时间尺度为1s，此时算法的误差较小。

设置SOC初始值为0.8，利用上述的EKF-UKF算法对锂电池进行在线参数辨识，得到

R

、

R

、

R

、

C

和

C

参数辨识结果，如图6和图7所示。

图6 R、R1、R2参数辨识结果

图7 C1和C2参数辨识结果

在模拟工况下，辨识前一阶段，特别是3 000次之前，电路模型的各个参数波动较为剧烈，这主要是由于模型参数初值选取不当造成的。3 000次之后，各模型参数逐渐稳定下来，没有剧烈的波动，逐渐趋于真实值，但之后电池模型参数并不是一个定值，这是因为电池系统的时变性，随着工作温度、循环次数等因素发生改变，模型参数也会随电池发生改变。

R

缓慢下降，

R

和

R

缓慢上升，并且

R

和

R

上升之和大于

R

下降值，这说明锂电池放电过程中，总电阻是增加的。

C

和

C

的变化趋势相同，先快速增加，后逐渐趋于平缓。

R

和

C

的乘积保持在几十，

R

和

C

的乘积保持在几百，所以此工况下模型的两时间常数

τ

和

τ

波动不大，并且

τ

大于

τ

。由上述分析可知，模型参数辨识结果是符合锂电池实际放电特性。

4.2 SOC估计结果分析

由于准确的SOC真实值无法获取，本文的安时积分法在与UDDS工况相近的温度和健康状态下进行，其SOC值与真实值最为接近，将其作为一种更接近真实值的方法参考比较。将UDDS工况下的电池电流和电压数据作为UKF-EKF算法和EKF算法的输入，算法运行后状态向量中的SOC估计结果与参考值的对比如图8所示。

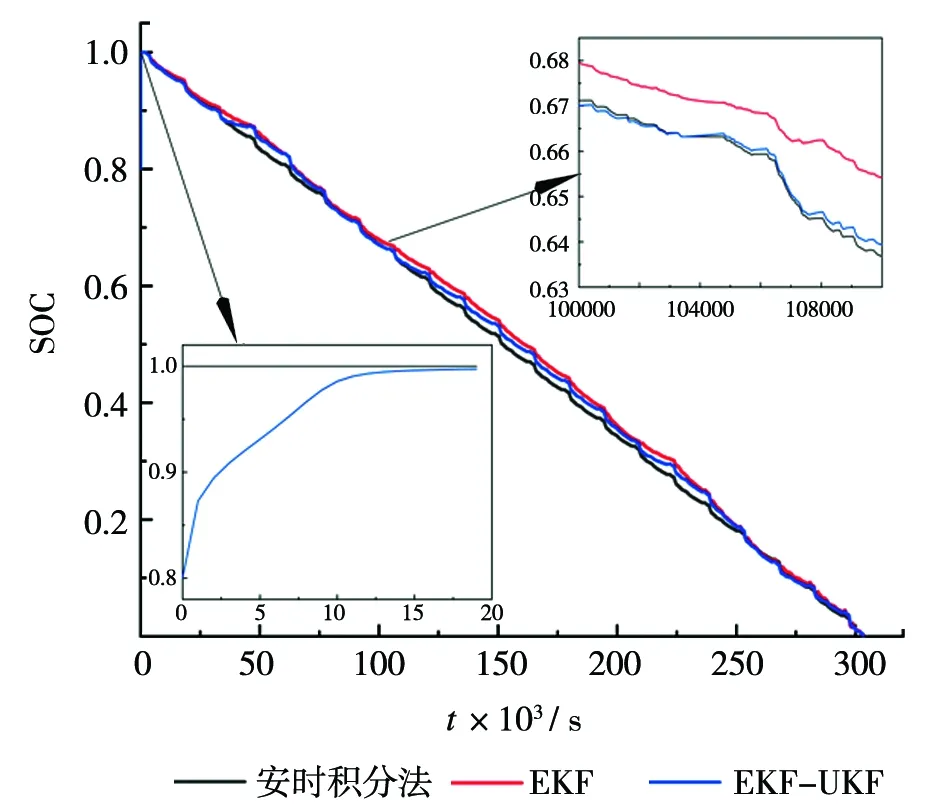
图8 SOC估计对比

在进行参数辨识前，先将SOC初始值设置为0.8，在SOC估计初始阶段，截取图中0～20s如图8所示。由于EKF-UKF算法参数在前60s内电池参数没有更新，仍和EKF算法采取相同参数初值，所以EKF-UKF算法和EKF算法跟踪效果相同。在60s后，EKF-UKF算法开始对参数进行在线参数辨识，参数进行实时更新，而EKF算法仍采用离线参数辨识，参数不变。取图8中大于60s的任意一段，例如当时间在100 000s～110 000s时，从图8可以清楚看出，EKF-UKF算法比EKF算法的估计值更接近参考值，说明EKF-UKF算法在线辨识的模型参数更接近实际工况下的模型参数，算法跟踪效果更好。为了更加精确分析两种算法对SOC的估计精度，图9给出了两种算法的SOC估计误差，EKF-UKF算法在整个工况过程的大部分时间内，SOC估计误差相较于EKF算法更小，并且EKF-UKF算法的估计误差的波动相较于EKF更小，这肯定与EKF-UKF算法能实时辨识模型参数有关。

图9 SOC估计误差

在UDDS工况下,通过对两种算法的SOC平均绝对误差和SOC误差均方根进行分析计算，得到EKF-UKF算法和EKF算法的平均绝对误差分别是0.90%和1.52%，EKF-UKF算法和EKF算法误差均方根分别是1.12%和1.80%。通过上述分析可知EKF-UKF算法相对EKF算法较精准且更稳定，表现出较好的精确性和鲁棒性。

5 结论

本文以二阶RC等效电路模型为基础建立了EKF-UKF联合算法，该算法相比与传统离线参数辨识算法，SOC估计的平均绝对误差和均方根误差都明显降低，解决了锂电池工作过程因参数变化造成的SOC估计精度差的问题，提高了算法的精确性和鲁棒性。

鉴于模型建立和SOC估计的实现都是恒温条件下进行的分析研究，没有考虑电池循环次数对锂电池参数的影响，后续将就锂电池温度和健康状态进行进一步研究以提高算法适用性。