基于系统动力学仿真的新冠肺炎防疫政策有效性研究

刘丹阳 张宁 牟宗玉

摘要：

2020年初中国爆发了新冠肺炎疫情，政府在不同时间采取各类防疫政策积极应对，政策的有效性决定了疫情能否得以控制。应用系统动力学方法构建了湖北省的疫情传播仿真模型，合理拟合了疫情发展的现实数据，并选取隔离防控政策、医疗政策以及无症状监测政策进行仿真实验，分析了“群体防疫”、单一政策和不同政策组合下疫情传播的特征，探讨了各类防疫政策的有效性。研究发现，每一项政策对此次疫情均起到了不同程度的抑制作用，但三项政策联合干预是最有效的。长期来看，在三项政策先后作用下，病毒的传播速率在短期内降低，感染者可被及时的隔离与救治，疫情得到有效控制的同时也缩短了疫情周期，并遏制了疫情的二次爆发。

关键词：

新冠肺炎;系统动力学;政策;仿真

中图分类号：N941.3

文献标志码：A

收稿日期：2020-08-28

基金项目：

山东省自然科学基金（批准号：ZR2017BG002）资助。

通信作者：

牟宗玉，男，博士，副教授，主要研究方向为物流与供应链管理等。 E-mail：mzydragon@163.com

新型冠状肺炎疫情作为一场全球战“疫”，引起了世界各国的广泛关注与高度重视。2020年2月11日，世界卫生组织（WHO）将由这类病毒作为病原体引发的疾病命名为COVID-19。COVID-19可通过呼吸道飞沫和接触传播[1]，极高的传染特性已严重威胁到人类的生命健康，为抑制新冠肺炎病毒的持续蔓延，中国政府出台并实施了多方面的非药物干预举措。一系列的防控举措可减少人口的流动，在一定程度上抑制了病毒在人与人之间的大规模扩散，但长期的隔离防控措施给人民的日常生活带来了诸多不便，国民经济也遭受到极大损失，因此及时判断干预措施的有效性，并模拟不同防疫政策下疫情的爆发趋势，对政府决策不同政策的持续时间具有重要意义。新冠肺炎疫情已蔓延至70多个国家，引起国内外学者的广泛关注。在中国新冠肺炎爆发初期，医疗专家就病毒特性展开研究，Li等[2-3]通过基因组数据监测以确定疫情的倍增时间与基本繁殖数。Tang等[4]利用传统的SEIR传染病动力学模型对湖北省疫情情况进行了模拟和评估。在此基础上，魏永越等[5-6]通过改进传统的SEIR傳染病动力学模型，更准确的预测新冠肺炎疫情的发展趋势，对防疫政策的制订提供了一定的科学依据。随着相关防疫政策的出台与实施，疫情的发展趋势逐渐偏离了以上传播动力学模型的预测结果，Fang等[7]通过数据驱动的方法来分析政府干预下疫情的传播动态，预测了极值的出现时间。耿辉等[8]利用Python建立SEIR模型来探究隔离防控措施的有效性。严阅等[9]考虑到病毒具有潜伏性、治疗具有周期性等特点，在改进的动力学模型的基础上引入了时滞过程。Koo等[10]通过模型研究，发现新加坡政府所实施的联合干预措施在当地新冠肺炎疫情防控中起到了重大作用。就目前来看，大部分文献均在建立传染病模型的基础上以预测隔离防控措施下的疫情发展趋势，没有考虑中国出台的关键防疫政策所带来的动态影响。本文利用Vensim建立新冠肺炎疫情系统动力学模型，在考虑到政策实施效果具有滞后性的基础上，选取了中国三项防疫政策，以模拟不同政策作用下的疫情发展趋势，并研究相关政策的有效性。

1 基于系统动力学的新冠肺炎传染模型的建立

系统动力学模型是通过探究不同因素之间的相互影响以模拟、预测系统结果，因此本文将研究对象确定为新冠肺炎的潜伏者、隔离者、有症状感染者、无症状感染者以及入院治疗者，建模对象为受此次疫情影响最严重的湖北省。

1.1 因果关系分析

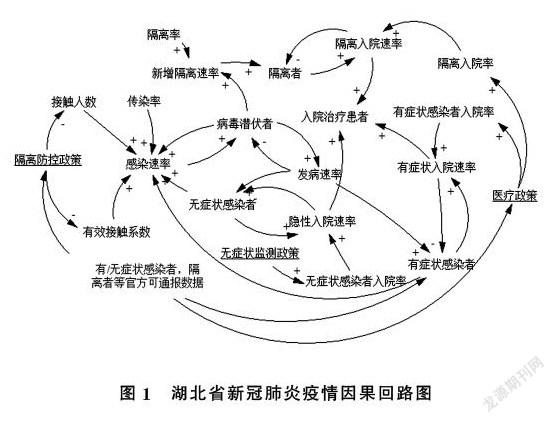
因果回路图如图1所示，本文将按照政策的不同来依次分析每种政策与不同研究对象之间的逻辑结构关系。其中“+”表示该变量的增加将引起另一变量的增加，“-”表示该变量的增加将引起另一变量的减少。

（1）隔离防控政策。该政策将影响接触人数和有效接触系数两个因素，且均为负反馈回路。隔离防控政策出台→-接触人数→-感染速率→-病毒潜伏者→-发病速率→-感染者数量;隔离防控政策出台→-有效接触系数→-感染速率→-病毒潜伏者→-发病速率→-感染者数量。

（2）医疗政策。该政策将影响隔离入院率和有症状者入院率两个因素，且均为负反馈回路。医疗政策出台→+隔离入院率→+隔离入院速率→-隔离者数量;医疗政策出台→+有症状者入院率→+有症状入院速率→-有症状者数量。

（3）无症状监测政策。该政策将影响无症状者入院率这一因素，且为负反馈回路。无症状监测政策出台→+无症状者入院率→+无症状入院速率→-无症状者数量。

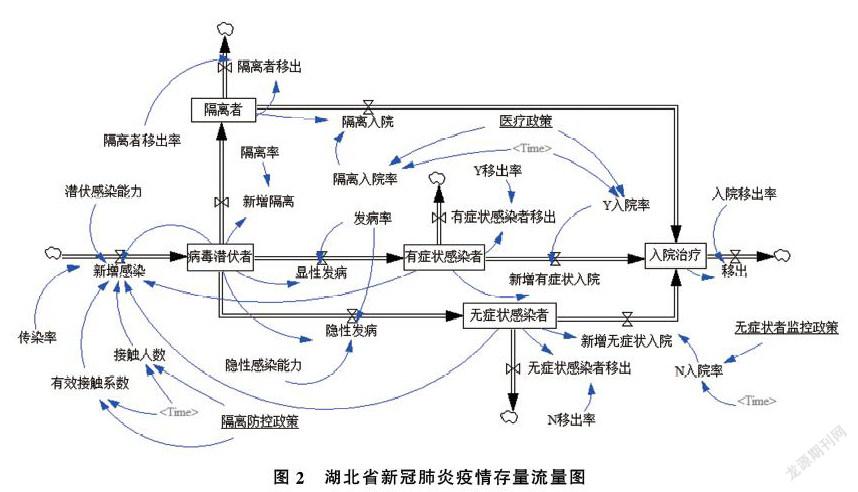
1.2 系统动力学存量流量关系构建

基于图1，绘制相应的存量流量图，本文以新冠肺炎的潜伏者、隔离者、有症状感染者、无症状感染者以及入院治疗者为存量，与之相应速率的升高和降低为流量，其他变量均为辅助变量与常量。存量流量图如图2所示，其中，Y表示有症状感染者，N表示无症状感染者。

1.3 模型参数设置

1.3.1 状态变量 （1）病毒潜伏者=INTEG（+新增感染-新增隔离-显性发病-隐形发病）; （2）隔离者=INTEG（+新增隔离-隔离入院-隔离者移出）; （3）有症状潜伏者=INTEG（+显性发病-有症状感染者移出-新增有症状入院）; （4）无症状感染者=INTEG（+隐形发病-无症状感染者移出-新增无症状入院）; （5）入院治疗=INTEG（+新增有症状入院+新增无症状入院+隔离入院-移出）。

1.3.2 速率变量 （1）新增感染=传染率×接触人数×有效接触系数×（有症状感染者+无症状感染者+病毒潜伏者×潜伏感染能力）;（2）新增隔离=病毒潜伏者×隔离率;（3）显性发病=病毒潜伏者×发病率;（4）隐形发病=病毒潜伏者×隔离率×隐性发病能力;（5）新增隔离/有症状入院/无症状入院=（隔离者/有症状感染者/无症状感染者）×（隔离入院率/Y入院率/N入院率）;（6）隔离者/有症状感染者/无症状感染者/入院移出者=（隔离者/有症状感染者/无症状感染者/入院治疗）×（隔离者移出率/Y移出率/N移出率/入院移出率）。

1.3.3 辅助变量及常量  （1）由于新型冠状病毒在传染初期数据统计并不完善，因此设定疫情起始时间为1月20日，即动力学模型所采用的初始数据来源于2020年1月20日湖北省卫生健康委员会官方网站疫情通报数据，具体数据取值及其设置依据见表1（官方数据来自湖北省卫生健康委员会官方网站[11];专家意见来自于中华预防医学会新型冠状病毒肺炎防控专家组[1]）。

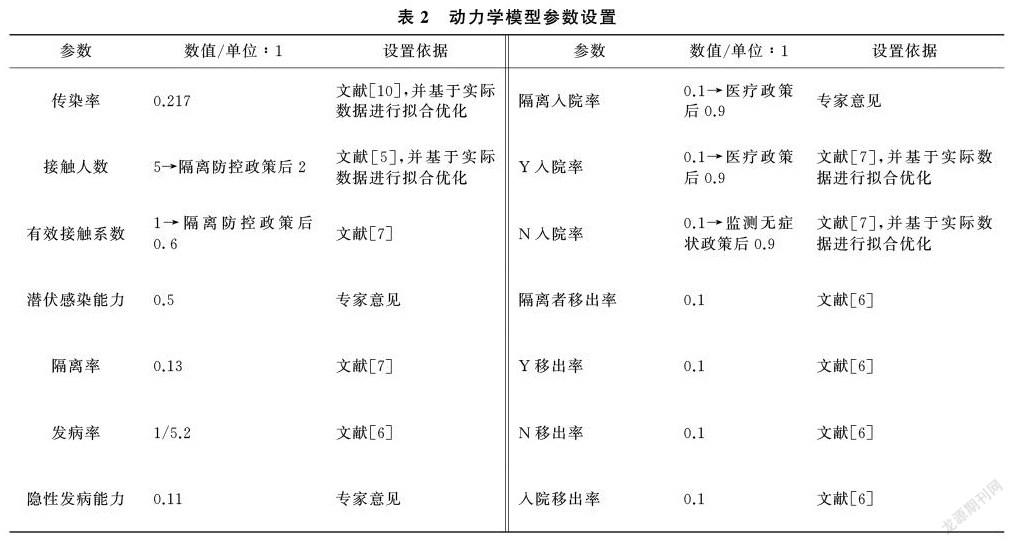
（2）结合参考文献、流行病学调查和专家意见等多方面信息，该系统动力学模型具体参数取值及其设置依据见表2（专家意见来自于中华预防医学会新型冠状病毒肺炎防控专家组[1];政策出台后部分变化参数数值均为基于实际数据进行拟合优化的假设值）。

1.4 模型及参数检验

为检验模型及所取参数的准确性，将表中数据代入该模型，以模拟湖北省的疫情爆发趋势。在疫情爆发的初始阶段，部分潜伏者与感染者均存在未检出患者，仅有入院治疗人数与官方数据一致，因此将入院治疗者总数作为检验模型以及所取参数准确性的重要指标。本文按照三项政策在不同时段的组合作用下模拟入院治疗人数在100天内的变化趋势，并采用同时段内官方公布的入院患者总数以验证模型。由于三项政策实施时间并不相同（本文设定政策实施日期分别为1月23日、2月5日和4月6日），且实施效果具有滞后性，因此设定三项政策分别在5、15、15天后政策实施效果达到最大化，参数数值呈线性变化。由图3，当前模型模拟的指标数与实际数据吻合程度较好，表明该系统动力学模型是有效的。

2 新冠肺炎防疫政策仿真分析

2.1 “群体防疫”状态下的新冠肺炎传染趋势分析

“群体防疫”状态表示在没有任何防疫政策下，仅考虑个人基本防护能力，以降低被感染的风险。假设从1月23日起，个人防护意识逐渐增强，并在两周后防护效果达到最大化，即接触人数从5人减少到2人，有效接触系数从1减少到09，数值呈线性变化。在“群体防疫”状态下新冠肺炎传染趋势如图4所示，潜伏者、感染者以及入院治疗患者的数量在100天内均呈现上升趋势，患者人数远超湖北省人口数量。这表明，在无任何防疫政策干预下，新冠肺炎疫情将蔓延整个湖北省，个人基本防护能力的强弱对患者数量的抑制作用并不明显。

2.2 单一防疫政策下的新冠肺炎传染趋势分析

2.2.1 隔离防控政策 随着新冠病毒疫情在武汉的快速传播，1月23日，武汉市实行封城政策，24日起，湖北省启动“重大突发公共卫生事件Ⅰ级响应”，根据突发公共卫生事件处理需要，对湖北省其他市、县采取必要的防控措施，暂停所有聚集性活动，防止病毒在人与人之间大规模扩散。由于该阶段政策措施出台时间紧凑，因此统称为 “隔离防控政策”，且设定实施时间为1月23日。在实行隔离防控政策下新冠肺炎传染趋势如图5所示，各患者的数量在100天内均呈现上升趋势，与无政策干预情形比较来看，患者数量大幅度减少，但仍远超实际数据。另外，在该政策实施效果达到最大化后的30天内，各患者的增长速率明显减缓，而30天后速率逐渐增长甚至超过起始速率。这表明隔离防控政策在短期内效果显著，但长期看来，只会推迟各患者峰值的时间，对患者数量的抑制作用并不明显。

2.2.2 医疗防控政策 疫情爆发后，湖北地区患者数量迅速增加，短缺的医疗物资和有限的床位使大量患者无法被有效隔离并治疗，意味着这群患者将面临错失最佳治疗时机并造成疫情扩散的双重压力。为此，国家部署雷神山、火神山以及方舱医院等医疗措施积极应对，并分别于2月3日、2月6日以及2月5日正式收治病人。由于三所医院投入使用日期相近，本文设定该政策实施时间为2月5日。在实行医疗政策下新冠肺炎传染趋势如图6所示，患者数量在100天内均呈现先升后降的发展趋势，与无政策干预情形比较来看，患者数量大幅度减少并得到一定控制，但仍远超实际数据。在第17～30天内，入院治疗患者的增长速率明显加快，而有症状感染者的数量在达到峰值后迅速下降，但在30天后下降速率明显减缓。这表明医疗政策出台后，有大量待入院的有症状感染者可得到治愈机会，并在30天之后达到较为平衡的状态，可见医疗政策在短期内效果并不明显，但长期看来，对各患者的峰值数起到一定的抑制作用。

2.2.3 无症状监测政策 在疫情爆发初期，由于无症状患者发病后无明显特征，在患者总数中所占比例较少，传染能力较弱，因此并没有得到重视。随着各項政策的实施，湖北省新增确诊病例逐渐减少，在加大监测力度的同时，无症状患者的确诊数量引起关注。4月6日，多地区出台了有关加强对无症状患者监测力度的政策文件，这意味着无症状患者的入院率将会有一定程度的提高。在实行无症状监测政策下新冠肺炎传染趋势如图7所示，患者数量在100天内均呈现上升趋势，与无政策干预情形相似，仅在该政策出台后的5天内，无症状感染者会到达一个峰值并在之后呈现下降趋势，但此现象维持时间较短，之后仍保持高增长速率。这表明无症状监测政策仅对短期内的无症状患者数量起到一定的抑制作用，但长期来看，对各患者数量的影响效果并不显著。

2.3 组合防疫政策下的新冠肺炎传染趋势分析

2.3.1 隔离、医疗政策 在实行隔离防控和医疗政策下新冠肺炎传染趋势如图8所示，患者数量相比较仅实施隔离防控政策而言都得到了有效地控制，且较符合实际数据。在第8天，病毒潜伏者的数量出现第一个峰值，有、无症状感染者的增长速率有不同程度的减缓，表明隔离防控政策效果凸显，对于患者的数量起到暂时性的抑制作用;病毒潜伏者的数量在第18天达到第二个峰值，之后开始呈现下降趋势，有、无症状感染者分别在第17天和第22天达到峰值，之后同样开始呈现下降趋势，这表明医疗政策效果凸显，在该政策实施效果达到最大化后的近30天，患者的增长速率明显减缓，对于患者的数量起到抑制作用。综上所述，隔离防控政策使得病毒的传播速率在短期内降低，医疗政策在病毒低传播阶段及时隔离与救治患者，进一步遏制了病毒的传播，长期来看，在两项政策先后作用下，疫情得到有效地控制。

2.3.2 隔离、无症状监测政策 在实行隔离防控和无症状监测政策下新冠肺炎传染趋势如图9所示，患者数量在100天内均呈现上升趋势，但相比较仅实施隔离防控政策而言，潜伏者与有症状感染者的数量都有不同程度的下降，但仍远超实际数据。在第8天左右，患者增长速率明显减缓，但到达中后期后速率逐渐增长甚至超过起始速率，表明隔离防控政策仅在短期内对疫情的发展起到一定的抑制效果;无症状感染者在82天会到达一个峰值，之后开始呈现下降趋势，这表明无症状监测政策短期内对无症狀患者的抑制效果凸显。综上所述，两项政策在不同时段的组合实施可以在短期内降低病毒的传播速率，长期来看，对患者数量的影响效果并不显著。

2.3.3 医疗、无症状监测政策 在实行医疗和无症状监测政策下新冠肺炎传染趋势如图10所示，各患者的数量在100天内均呈现先升后降的发展趋势，与仅实施医疗政策而言，感染者的数量在后期有不同程度的下降，但仍远超实际数据。在第82天，无症状感染者的下降速率明显加快，表明无症状监测政策短期内对无症状患者的抑制效果凸显。综上所述，两项政策在不同时段的组合实施可以加快各患者峰值的到达，并对峰值数起到一定的抑制作用。

2.3.4 隔离、医疗、无症状监测政策 在三项政策联合作用下新冠肺炎传染趋势如图11所示，各患者的数量均得到有效控制，且符合实际数据。在疫情发展的后期，无症状感染者的下降速率增加，这表明监测无症状患者政策对疫情发展的后期有一定的抑制作用。综上所述，隔离防控政策使得病毒的传播速率在短期内降低，医疗政策在病毒低传播阶段及时隔离与救治患者，进一步遏制了病毒的传播，而无症状监测政策消除隐性感染者隐患，并缩短了疫情周期，长期来看，在三项政策先后作用下，疫情得到有效地控制，并遏制了疫情的二次爆发。

3 防疫政策有效性分析与优化

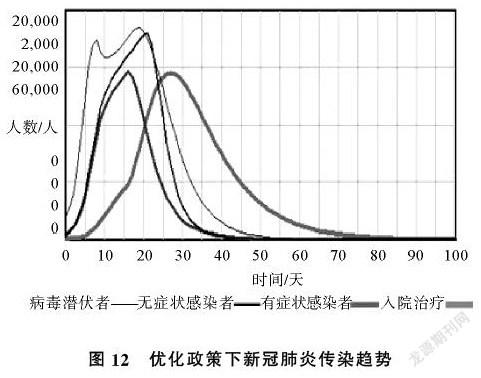
隔离防控政策与医疗政策对此次疫情的防控与治疗两方面影响效果显著，但由于无症状患者政策出台较晚，且后期各类患者数量较少等原因，对此次疫情的影响较小。本文对影响效果不显著的政策进行优化，以便准确验证防疫政策的有效性。即假设将无症状监测政策出台时间提前60天，以模拟组合防疫政策优化作用下的疫情爆发趋势。在优化政策下新冠肺炎传染趋势如图12所示，无症状感染者的峰值在第21天约为1 850人，与政策未优化相比较，达到峰值时间提前了2天，减少了约50人;入院治疗者的峰值在第27天约为44 000人，与政策未优化相比较，大多数无症状感染者得到入院治疗机会，增加了约1 000人;其他患者峰值并无明显变化。相比较而言，病毒潜伏者、无症状患者以及入院治疗者在到达峰值后的下降速率明显加快，且在第90天左右，疫情结束。这表明优化后的无症状监测政策在疫情发展中期效果凸显。综上所述，在联合政策优化实施下，不仅有效遏制了病毒的传播，疫情的防控与救治能力均得到进一步提高，疫情得到有效控制，并缩短了疫情发展周期。

4 结论

本文通过Vensim建立新冠肺炎疫情系统动力学模型，模拟不同政策作用下此次疫情的发展趋势。对比分析可知，与无防疫政策情形相比，隔离防控政策仅在短期内效果显著;医疗政策使得大量待入院的有症状感染者得到治愈机会，长期看来，对各患者的峰值数起到一定的抑制作用;无症状监测政策仅对短期内的无症状患者数量起到一定的抑制作用。因此，在三种政策联合干预下疫情得到有效地控制，并遏制了疫情的二次爆发。

参考文献

[1]中华预防医学会新型冠状病毒肺炎防控专家组. 新型冠状病毒肺炎流行病学特征的最新认识[J]. 中国病毒病杂志， 2020， 10（2）： 86-92.

[2]LI Q， GUAN X， WU P， et al. Early transmission dynamics in Wuhan， China， of novel coronavirus-infected pneumonia[J]. The New England Journal of Medicine， 2020; 382：1199-1207.

[3]LI X， WANG W， ZHAO X. et al. Transmission dynamics and evolutionary history of 2019-nCoV[J]. Journal of Medical Virology， 2020， 92（5）： 501-511.

[4]TANG B， WANG X， LI Q， et al. Estimation of the transmission risk of 2019-nCov and its implication for public health interventions[J]. Journal of Clinical Medicine， 2020， 9（2）： 462.

[5]魏永越， 卢珍珍， 杜志成， 等. 基于改进的SEIR～（+CAQ）传染病动力学模型进行新型冠状病毒肺炎疫情趋势分析[J]. 中华流行病学杂志， 2020， 41（4）： 470-475.

[6]曹盛力，冯沛华，时朋朋. 修正SEIR传染病动力学模型应用于湖北省2019冠状病毒病（COVID-19）疫情预测和评估[J]. 浙江大学学报（医学版）， 2020， 49（2）： 178-184.

[7]FANG Y， NIE Y， PENNY M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions： A data-driven analysis[J]. Journal of Medical Virology. 2020， 92（6）：645-659.

[8]耿辉， 徐安定， 王晓艳， 等. 基于SEIR模型分析相关干预措施在新型冠状病毒肺炎疫情中的作用[J].暨南大学学报（自然科学与医学版）， 2020， 41（2）：175-180.

[9]严阅， 陈瑜， 刘可伋， 等. 基于一类时滞动力学系统对新型冠状病毒肺炎疫情的建模和预测[J]. 中國科学：数学， 2020， 50（3）：385-392.

[10] KOO J R， ALEX R C，MINAH D， et al. Interventions to mitigate early spread of SARS-CoV-2 in Singapore： a modelling study[J]. Lancet Infection Diseases I， 2020， 20（6）： 678-688.

[11] 湖北省卫生健康委员会. 疫情防控最新动态[EB/OL]. [2020-07-21]. http：//wjw.hubei.gov.cn/bmdt/dtyw/202009/t20200921_2916940.shtml.

Abstract：

The COVID-19 epidemic broke out in China at the beginning of 2020. Various epidemic prevention policies were adopted by the government at different times. Whether the epidemic could be controlled depends on the effectiveness of the policies. Hubei province epidemic spread simulation model was conducted by the system dynamics methods. The actual data of epidemic development were reasonably fitted. The simulation experiments of "quarantine and prevention policy"， "medical policy" and "asymptomatic monitoring policy" were carried out， and the effectiveness of various epidemic prevention policies is discussed. As the research results show， each policy had a different degree of inhibition on the outbreak. It is remarkable that the three policy interventions are the most effective. In the long run， under the three policies， the transmission rate of the virus was reduced in the short term， the infected people could be isolated and treated in time， and the epidemic period was shortened while the epidemic was effectively controlled， and the secondary outbreak of the epidemic was prevented.

Keywords：

COVID-19; system dynamics; policy; simulation