基于牛顿冷却定律研究回焊炉材料的炉温曲线

尹 硕，张德顺

(石河子大学 理学院，新疆 石河子 832000)

在集成电路板等电子产品生产中，需要将安装有各种电子元件的印刷电路板放置在回焊炉中，通过加热，将电子元件自动焊接到电路板上. 在生产过程中，让回焊炉的各部分保持工艺要求的温度，对产品质量至关重要. 目前，这方面的许多工作通过实验测试的方法来进行控制和调整. 此物理背景为2020年高教杯全国大学生数学建模竞赛试题[1]，旨在通过构建机理模型来进行分析研究，利用牛顿冷却定律建立焊点与环境之间的热交换模型[2-5]，在求解回焊炉内部焊点温度随时间变化的炉温曲线中有参考意义.

1 模型背景

回焊炉内部设置若干个小温区，从功能上可分成4个大温区：预热区、恒温区、回流区、冷却区. 电路板两侧搭在传送带上匀速进入炉内进行加热焊接. 回焊炉内一般有11个小温区及炉前区域和炉后区域，每个小温区长度为30.5 cm，相邻小温区之间有5.0 cm的间隙，炉前区域和炉后区域长度均为25.0 cm. 回焊炉启动后，炉内空气温度会在短时间内达到稳定，稳定后，回焊炉方可进行焊接工作. 炉前区域、炉后区域以及小温区之间的间隙无特殊的温度控制，其温度与相邻温区的温度有关，各温区边界附近的温度也可能受到相邻温区温度的影响[6-7]. 另外，生产车间的温度保持在25 ℃.

在设定各温区的温度和传送带的过炉速度后，可以通过温度传感器测试某些位置上焊接区域中心的温度，称之为炉温曲线(即焊接区域中心的温度曲线). 各温区设定的温度分别为175 ℃(小温区1～5)、195 ℃(小温区6)、235 ℃(小温区7)、255 ℃(小温区8～9)及25 ℃(小温区10～11)；传送带的过炉速度为70 cm/min；焊接区域的厚度为0.15 mm. 温度传感器在焊接区域中心的温度达到30 ℃时开始工作，电路板进入回焊炉时开始计时.

2 模型建立

现讨论热传导的相关数学模型如图1所示，已知温度值u是关于电路板在传送带上的位置x与时间t的二元函数，选取炉前区域的起始点为坐标原点.现使用热传导原理推导回焊炉内相邻温区间隙的温度u关于位置x的函数关系[8],根据能量守恒定律可得

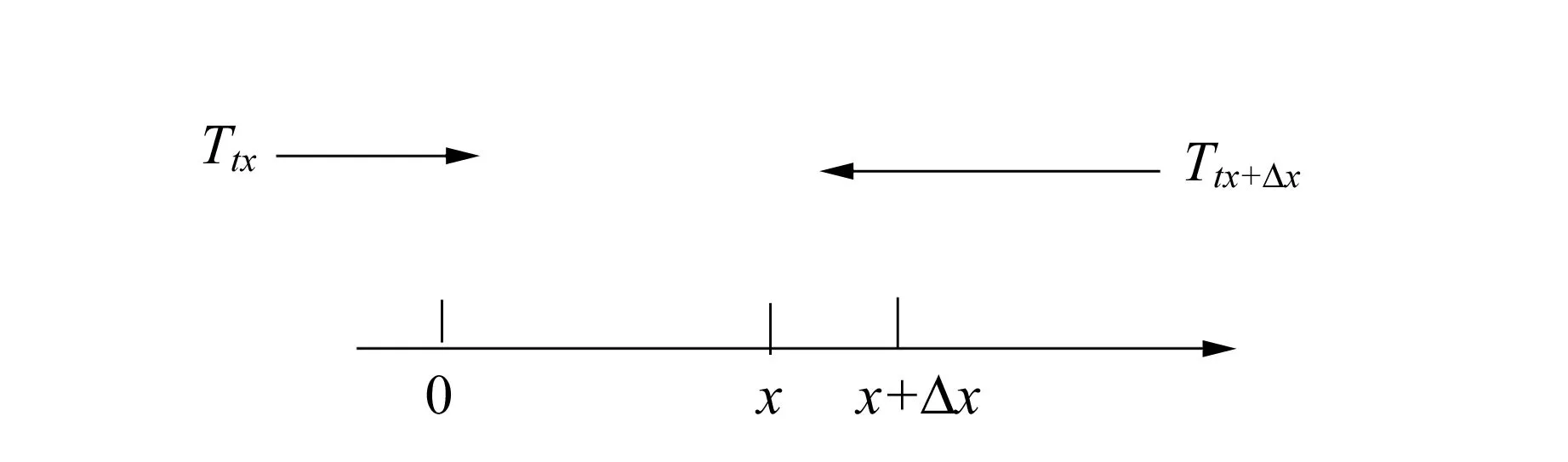
图1 一维空间下热传导坐标图

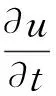
(1)

其中C为物质比热容，ρ为物质密度，k为热传导系数，u为炉内有温度变化缝隙区域的温度值.

初始时刻t=0时各处温度值为τ0，任一时刻在原点位置处的温度值为τ1，在位置l处的温度值为τ2.一维空间中，回焊炉中电路板的泛定方程和定解条件为：

(2)

解得温度值为

(3)

其中Cn为常量，an为本征值，l为缝隙区域长度.

若使回焊炉内各个部分区域温度稳定，就要使回焊炉启动足够长的时间.假定回焊炉已经开启足够长时间，则式(3)中t→∞，分析可得温度函数是关于电路板位置坐标的线性函数，与图像的拟合程度很好.

通过实际拟合情况推知,在炉前区域的温度变化图像符合指数增长趋势；在预热区、恒温区、回流区和冷却区之间缝隙的温度变化图像符合线性增长趋势.由此得出温度分布函数及其图像如图2所示.在炉前区环境温度随电路板位置呈指数关系上升，在保温区保持稳定，在回流区出现稳定和线性函数关系，在冷却区呈现固定的温度.图2中环境温度随电路板位置x变化的函数为

(4)

焊接区域的中心温度在预热区先呈指数函数上升；到达保温区，温度以较小斜率上升；在小温区3中点处，焊接中心的温度为168.19 ℃；在小温区6中点处，焊接中心的温度为168.19 ℃；在小温区7中点处，焊接中心的温度为188.19 ℃；在小温区8结束处，焊接中心温度为214.97 ℃. 焊接区域的中心温度变化情况可以通过以时间为自变量，以中心温度为因变量做预测炉温曲线，如图3所示.

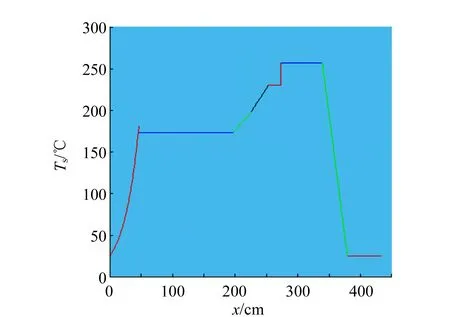
图2 环境温度随电路板位置变化的坐标函数图像

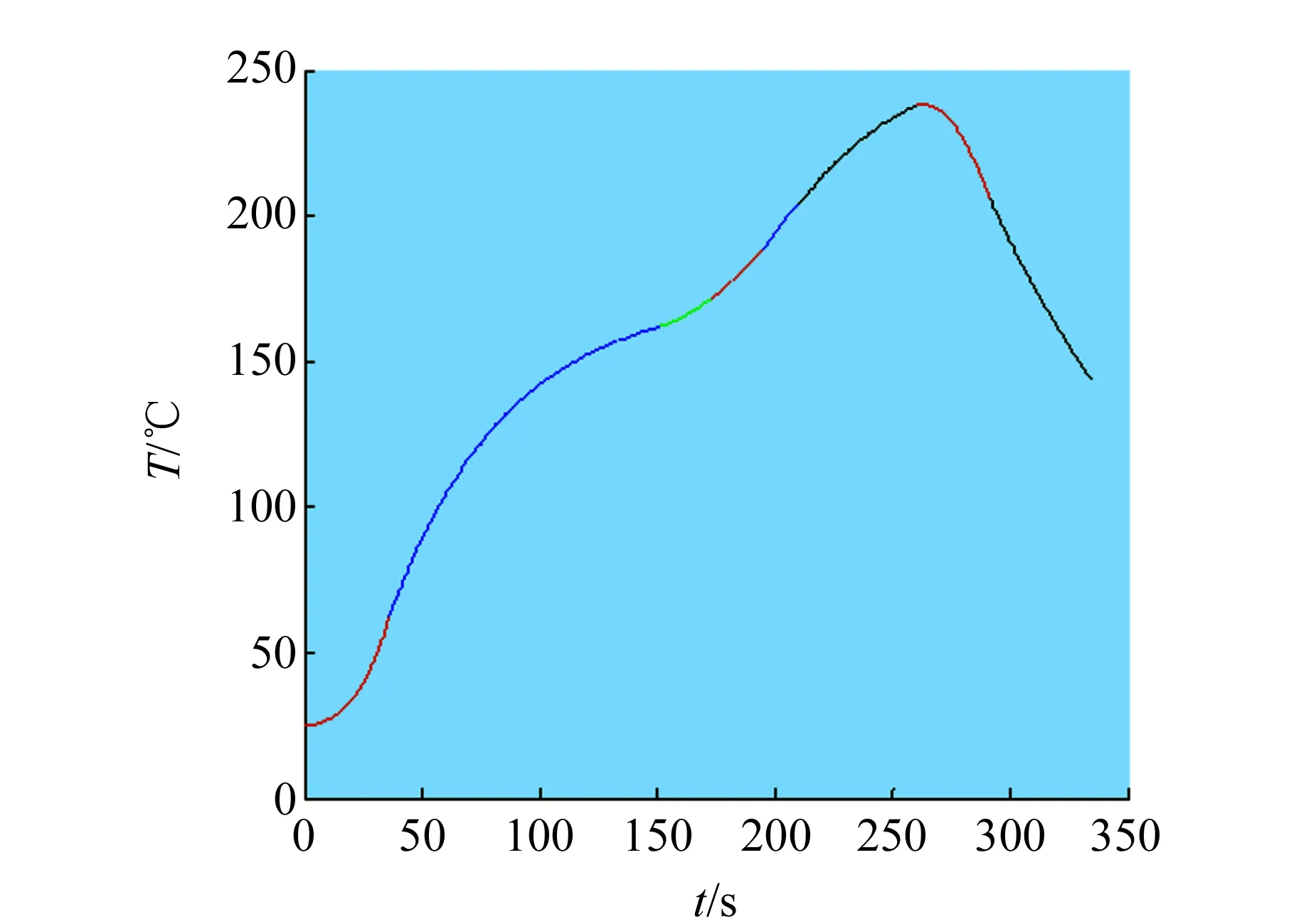
图3 炉温曲线变化情况

为方便建立数学模型，统计得到传送带上8个节点距离原点的距离，如表1所示.

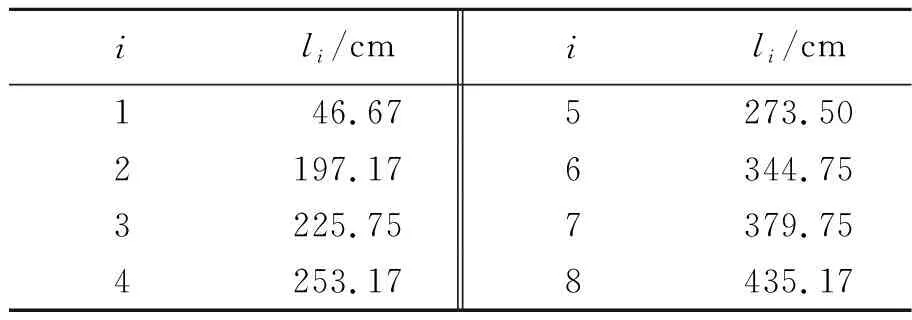
表1 节点距原点的距离

设Tn(n=1,2,…,8)表示电路板在各个分段区间上末端温度的最大值，通过建立焊接温度的最大值与各个温区传送带速率的函数关系，计算、整理得：

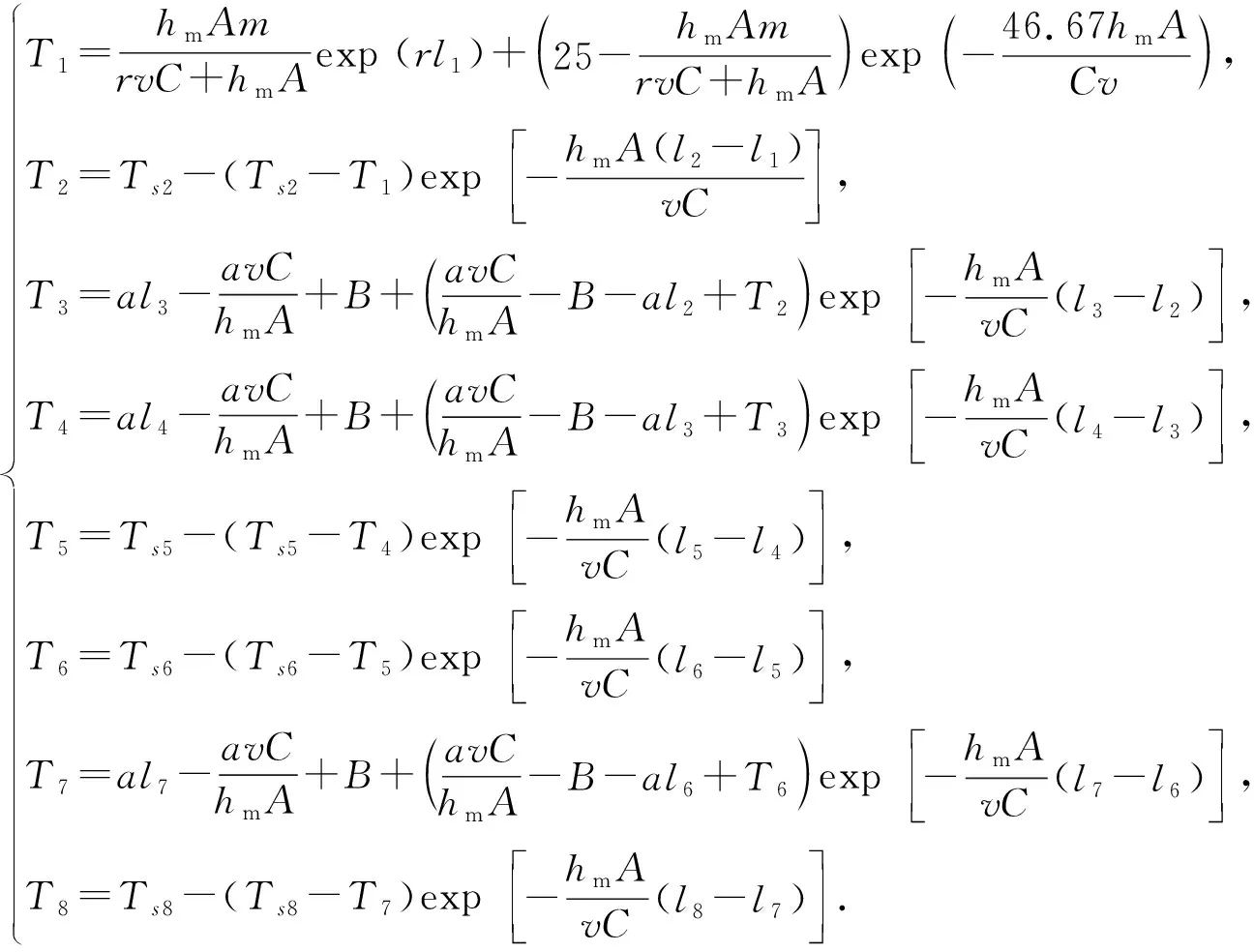
(5)

其中,hm为平均对流换热系数，v为传送带速度(cm/s),A,m,r,a,B均为常数.通过将已知参量代入式(5)中，经计算得出结论：将参量代入T6函数，可知大约在第9温区的末端位置时的传送带移动速度最大.

3 模型计算与检验

为了方便判断焊接中心所在位置随时间的变化，通过Java计算出焊接中心进入各温度区的时间以及出温度区的时间，如表2所示.

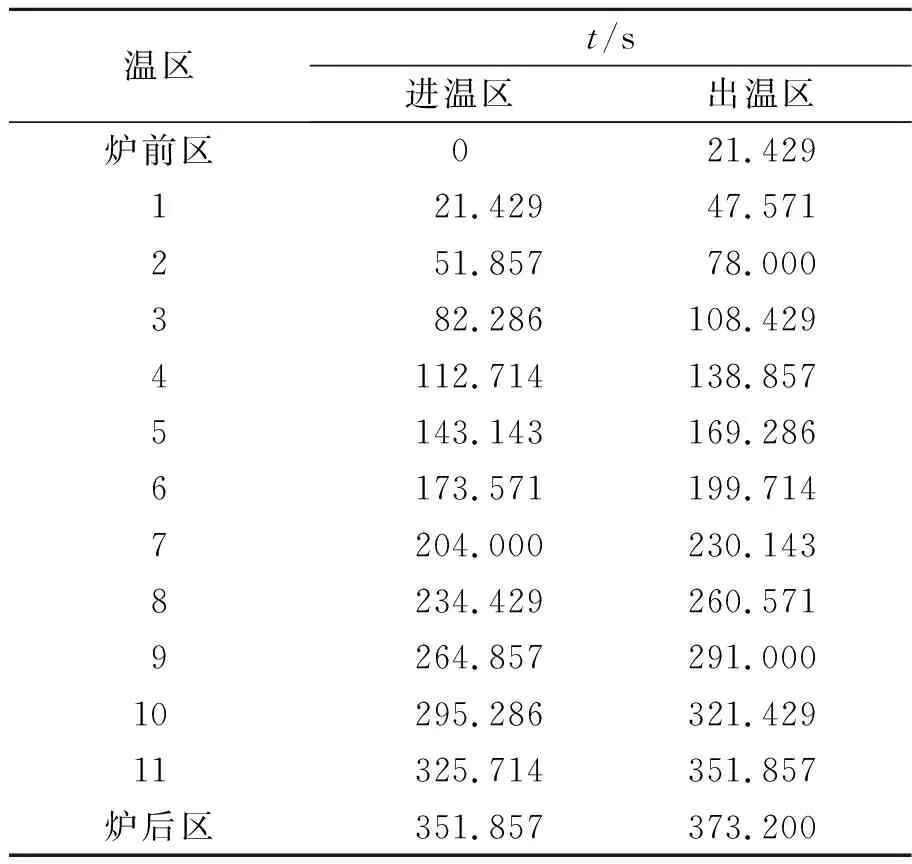
表2 材料焊接中心的进出温区时间情况

现应用建立的数学模型对实际情况进行分析拟合，并检验该模型的正确性与可行性.

通过对数据的分析，发现在1～5区之间存在环境温度保持不变的区间，在图2中很明显地看出终端处于150.0～175.0 ℃之间，左边曲线斜率增长缓慢，右边曲线斜率增长迅速，同样可推测出1区中的温度并不是都相等，而受到外界环境温度的影响，通过Matlab工具箱精确测出符合第1部分的区间为40.0～169.0s，其函数模拟曲线如图4所示.

图4 40.0～169.0 s的焊炉曲线模拟图

在曲线模拟过程中，可以求得模拟曲线函数为：

T=64.75+(175-64.75)·

(6)

此函数所得到的图像与实际图像几乎重合(R2=0.999 9)，说明在这一时间内符合推理，记录时间的起止时间为40.0～169.0 s. 继续使用Matlab拟合数据，试图寻找是否还存在环境温度保持不变的情况，最终得到如下的拟合结果:在217.0～234.5 s,234.5～291.0 s,325.5～373.2 s内，环境温度均保持恒定，曲线拟合图分别为图5～7所示.

对图5进行曲线模拟，可以求得模拟曲线函数为

T=193.76+(235-193.76)·

(7)

此函数所得到的图像与实际图像几乎重合(R2=0.999 8)，说明在这一时间内同样符合上述公式推理，记录起止时间为217.0～234.5 s.

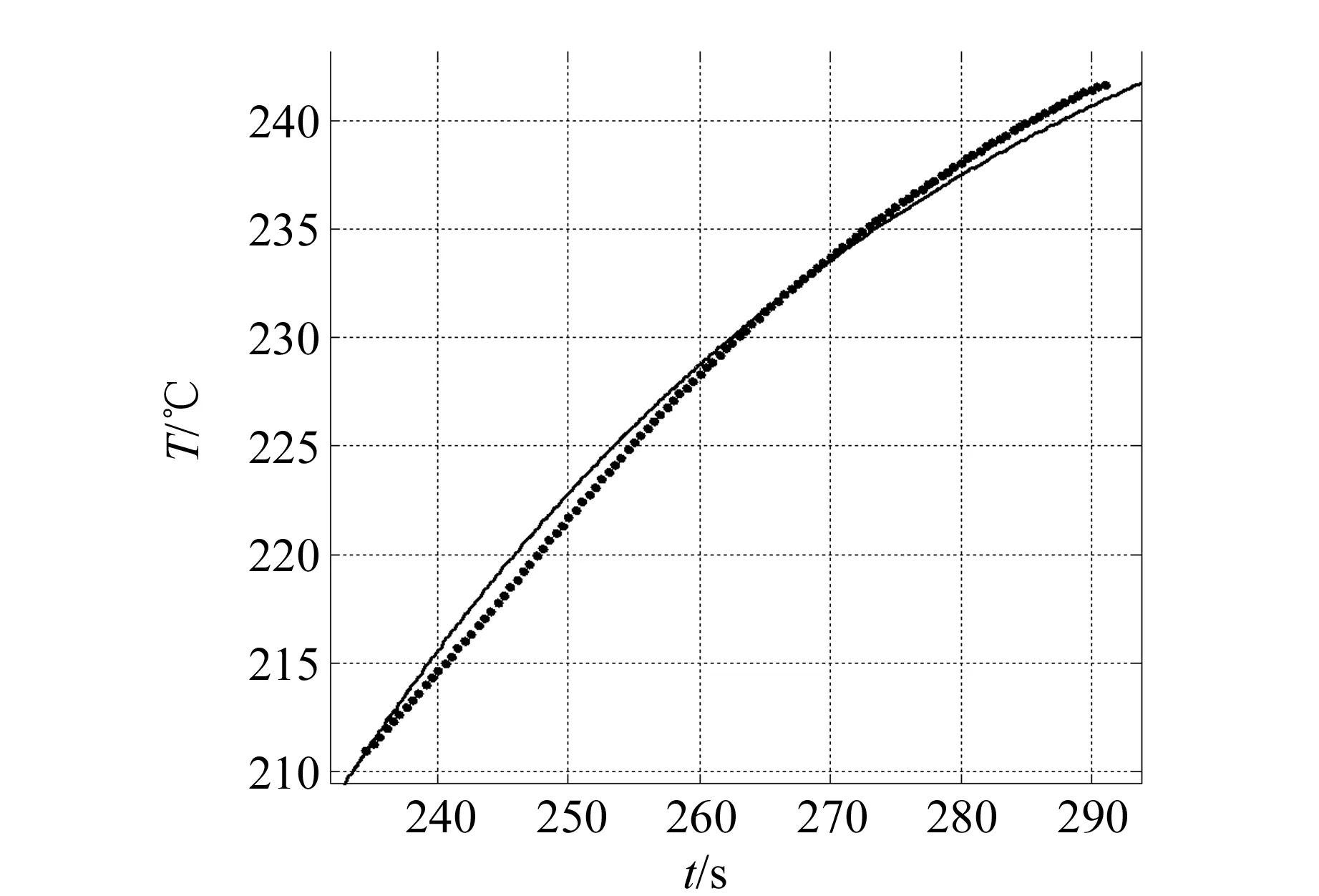
图5 217.0～234.5 s的焊炉曲线拟合图

对图6进行曲线模拟，可以求得模拟曲线函数为：

T=210.91+(255-210.91)·

(8)

此函数所得到的图像与实际图像重合较好(R2=0.993 9)，说明在这一时间内同样符合上述公式推理，记录起止时间为234.5～291.0 s.

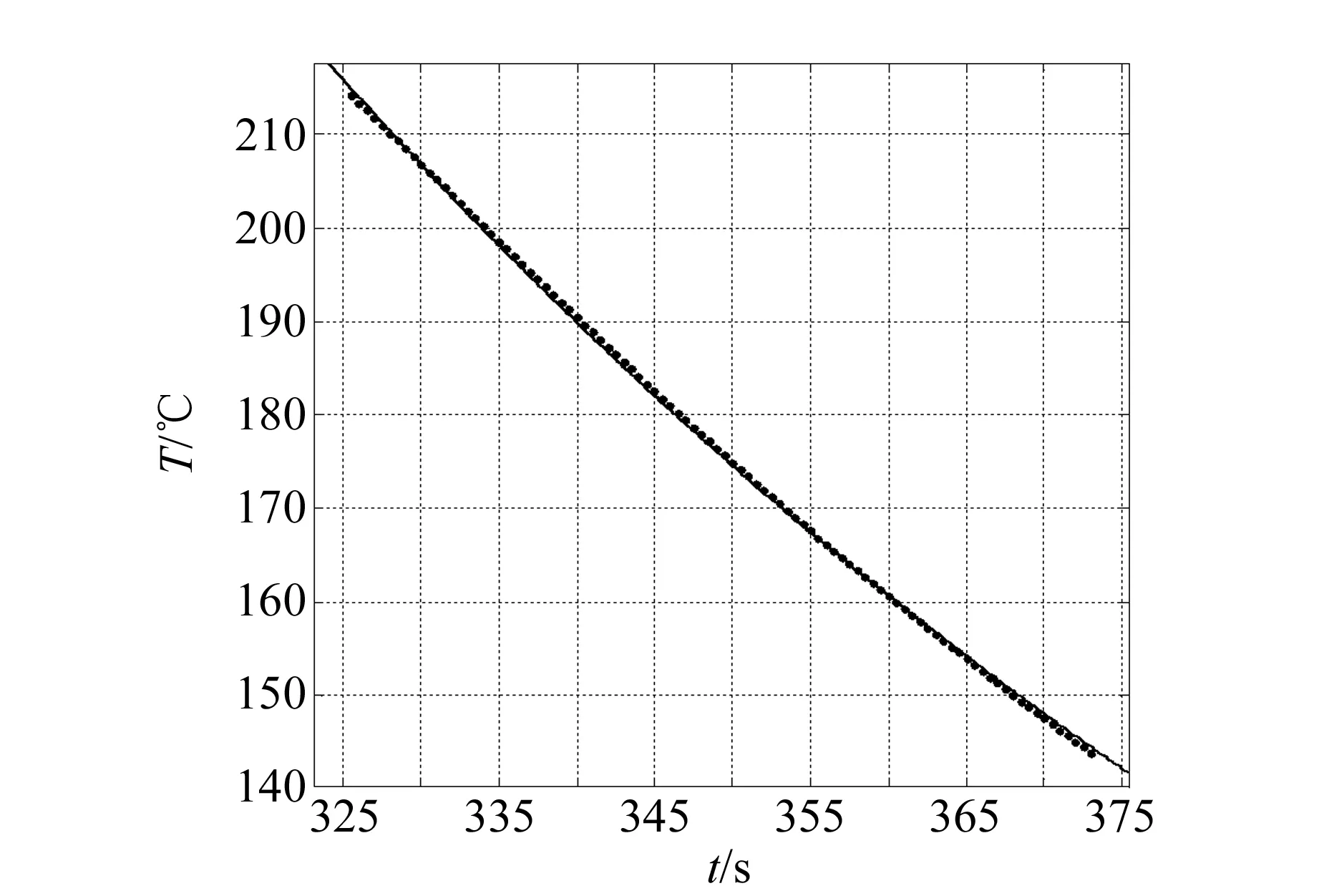
图6 234.5～291.0 s的焊炉曲线拟合图像

对图7进行曲线模拟，可以求得模拟曲线函数为

T=214.97+(25-214.97)·

(9)

此函数所得到的图像与实际图像重合较好(R2=0.999 6)，说明在这一时间内符合上述公式推导，记录起止时间为325.5～373.2 s.

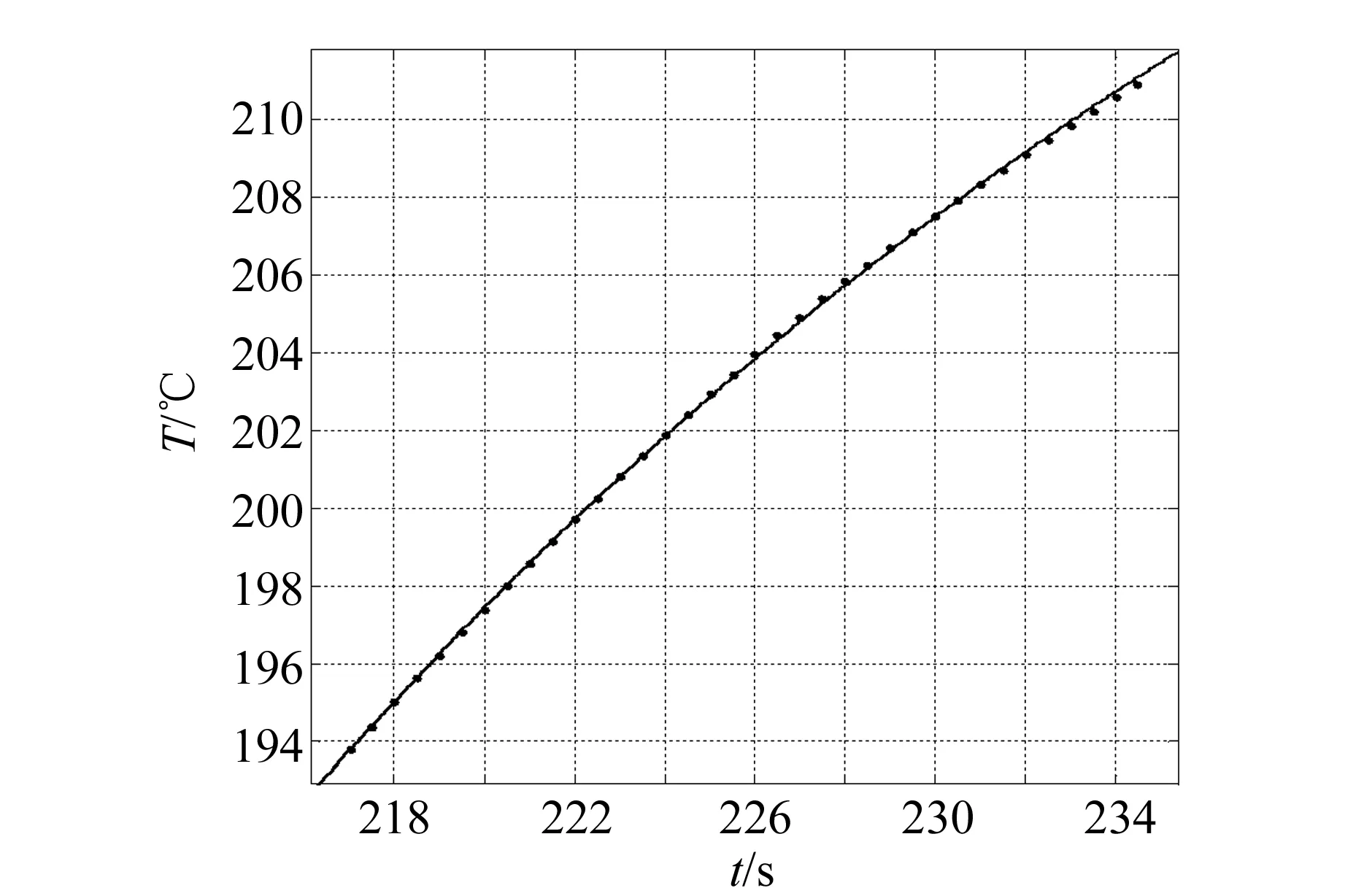
图7 325.5～373.2 s的焊炉曲线拟合图像

利用上述方程组拟合其他温度变化缝隙的炉温曲线，发现拟合程度较好，其函数图像与工业实际生产线情况基本吻合，可证明函数关系的正确性和合理性.

4 结束语

本文研究了多温区回温炉的各温区设定的温度及其传送速度的设定对焊炉曲线函数的影响,查找分析现有资料得知回焊炉与电路板之间主要通过热对流的方式传导热量,通过对炉温曲线问题的求解,利用牛顿冷却定律得到了焊点温度与环境温度之间的常微分方程，求解该方程得到了焊接区域与环境之间的热交换模型,通过分段拟合的方式发现此模型仅在加热区与实际温度符合得较好并给出了环境温度随时间呈线性变化的关系以及对应的热交换模型，至于环境温度与时间为非线性关系时的分析亦可与以上讨论相类比[9]. 通过此理论模型求解出的预测炉温曲线与实际炉温曲线拟合程度较好，具有较高的可信度.