磁热效应模拟仿真实验

高 源，钱建强

(北京航空航天大学 a.高等理工学院;b.物理学院，北京 100191)

绝热条件下，磁性物质温度随着外加磁场强度改变而改变的现象称为磁热效应. 磁热效应制冷被认为是获得低温的主要手段之一，利用磁热效应制造的绝热退磁制冷机[1]可以将温度降低到50 mK. 大部分地表实验仪器采用3He-4He稀释制冷，但该方法存在极低温制冷时液氦的损耗和对重力的依赖等问题. 在太空环境中航天器处于失重状态，稀释制冷机无法正常工作，因此在航天应用方面多采用以顺磁盐为工作介质的绝热退磁制冷机. 绝热退磁制冷机利用顺磁盐在零场处的相变进行制冷，时至今日，顺磁盐的磁热效应依然是获取低温的主流手段之一. 随着对量子磁性认识的深入，人们发现关联量子材料在有限场处的量子相变也会产生类似的磁热或逆磁热效应. 由于该实验存在安全性低、成本高等问题，因此学生较难接触到低温环境. 为了激发学生对磁热效应的兴趣，使其了解更多相关知识，本文通过解析计算和张量网络重正化群算法，对3种材料的低温热力学性质进行计算，结合疫情期间线上教学所采用的仿真实验技术[2-3]，建立了磁热效应测量仿真平台.

1 仿真平台的原理

利用磁热效应建立的绝热退磁制冷机的理想工作流程如图1所示，图中彩色曲线为硫酸铁铵在不同磁场下的熵曲线，对应的磁场值标记在曲线旁，图中黑色线为1次完整制冷循环，具体流程如下:

1)A→B：等温加磁场，工作介质向热沉放热.到达B点后断开与热沉的连接；

2)B→C:绝热退磁，直到温度下降到探测器的工作温度，即C点.达到C点后打开工作介质与探测器的连接；

3)C→D:等温退磁，使探测器维持在工作温度以进行相关测量，到达D点后断开与探测器的连接；

4)D→A:绝热加磁场，升温到A点后开启与热沉的连接，开始下一轮循环.

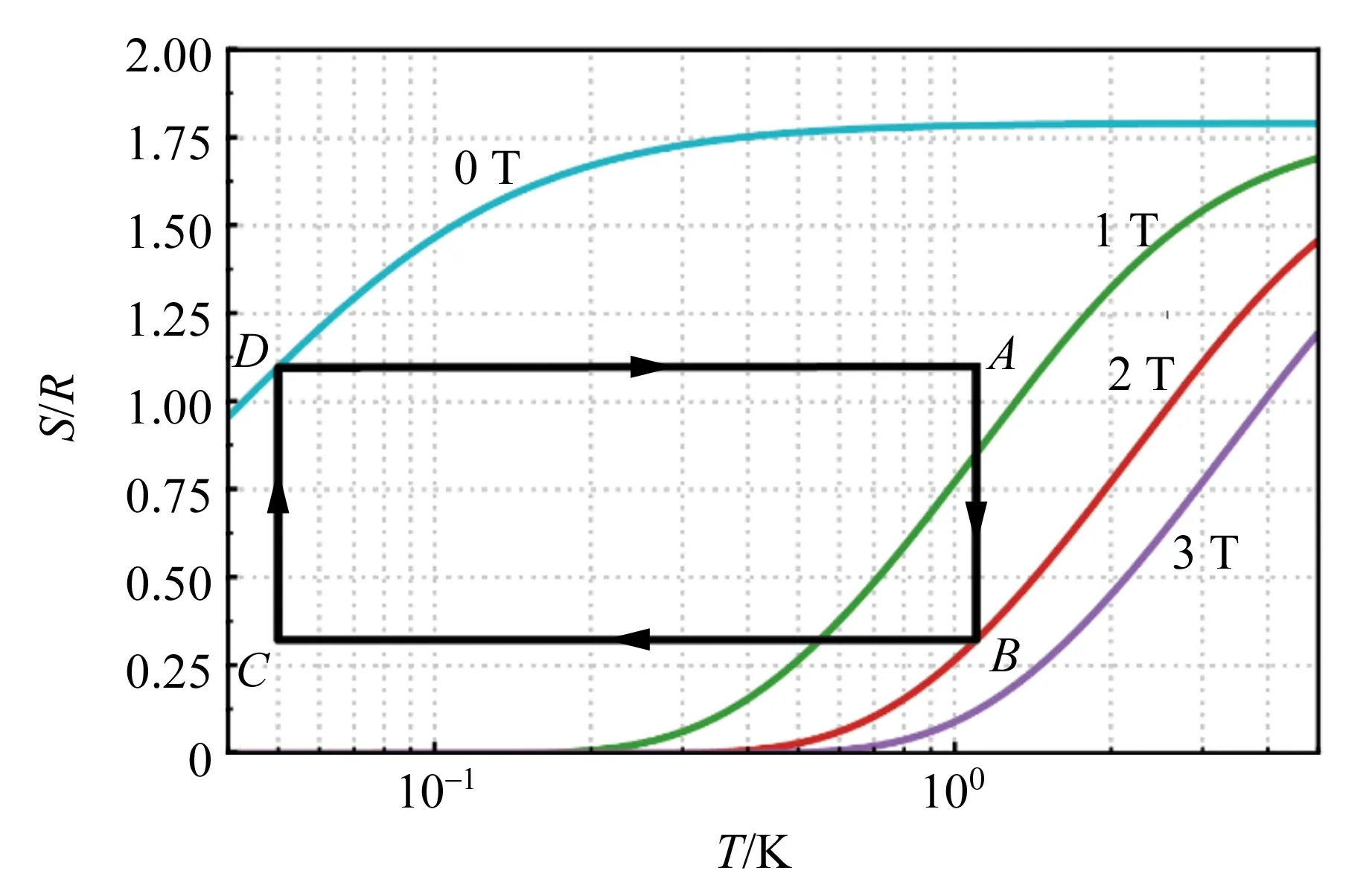
图1 绝热退磁制冷机工作原理示意图

对工作介质性能的评价主要有2点：a.绝热温变，这决定了其能到达的最低温度；b.等温熵变，这决定了其在工作温度的吸热量. 二者均可由温熵图体现. 除了工作介质以外，绝热退磁制冷机还需要保护层，其主要作用为吸收热库、连接设备等器材的漏热，为工作介质提供温度低于热库的外部环境. 保护层材料要求具有较大的热容与热导，可以在快速吸热的同时尽量缓慢地升温. 热容的大小可以体现在熵变的快慢上，而热导的计算较为复杂，在此不做讨论. 无论对于工作介质还是保护层，其工作效能均可以由熵曲线进行刻画，因此磁热效应仿真的核心在于对体系熵曲线的精确计算.

目前所采用的制冷材料主要为硫酸铁铵(ferric ammonium alum, FAA)和钆镓石榴石[1](gadolinium gallium garnet, GGG),这2种材料的低温热力学性质均可以用顺磁盐模型来描述. 但在实际应用过程中，顺磁盐的零场热容、热导以及对磁场的利用率等方面均存在不足. 其原因是材料中自旋(赝自旋)之间几乎没有相互作用. 关联量子材料由于电子之间存在相互作用，其零场热容会优于顺磁盐，在作为保护层时更加有效. 在量子临界点附近，关联量子多体系统存在大量低能激发，这些低能激发可以使材料具有较大的热导率[4].

提供的仿真材料有3种，分别为FAA、GGG和Cu(NO3)2·2.5H2O. 其中FAA是自旋5/2的顺磁盐；GGG是自旋7/2的自旋液体[5]，由于其实验数据可以被顺磁盐模型较好拟合，因此在本文中也当作顺磁盐处理；Cu(NO3)2·2.5H2O具有交替海森堡反铁磁链[6]，利用张量网络重正化群算法可以很好地计算其低温热力学性质.

1.1 顺磁盐仿真原理

顺磁盐的哈密顿量一般表示为

(1)

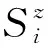
本文研究的2种材料的熵可以利用如下公式进行计算[1]:

(2J+1)xcoth [(2J+1)x],

(2)

(3)

(4)

其中，n为总粒子数，J为自旋量子数，B为外加场的磁感应强度，b为内建修正场的磁感应强度，μB为波尔磁子，kB为玻尔兹曼常量，T为温度.对于FAA而言，b具有如下形式:

(5)

其中，b0=0.056 T，T0=0.060 1 K，a=0.377.对于GGG而言，b=0.481 T[7-8].

顺磁盐存在奈尔温度，当温度低于奈尔温度，体系会脱离顺磁相而形成反铁磁序.此时上述计算不再适用.因此在仿真时，要求体系的温度高于材料的奈尔温度，FAA的奈尔温度为0.026 K，GGG的奈尔温度为0.38 K.

1.2 Cu(NO3)2·2.5H2O仿真原理

Cu(NO3)2·2.5H2O具有交替海森堡反铁磁链，其哈密顿量为:

(6)

将其分解为奇偶2部分，即：

(7)

(8)

利用Trotter-Suzuki[9]分解，其密度矩阵的计算可以近似为

ρβ=exp (-βH)≈

[exp (-τHodd)·exp (-τHeven)]N.

(9)

其中N为充分大的整数且满足β=Nτ.利用矩 阵乘积算符(matrix product operator, MPO)来表示密度矩阵和演化算符，便得到二维张量网络.对于张量网络的收缩，采用双层无限长线性张量网络重正化群算法(bilayer infinite-size linearized tensor renormalization group, iLTRG)[10-11]. 双层算法中对密度矩阵的计算有:

(10)

相较于单层算法，双层算法中张量网络的正则形式提高了其稳定性.同时只需要演化到β/2即可计算β处的热力学量，降低了计算复杂度. 对于给定磁场，熵曲线的计算在几十秒到几分钟之间.

考虑到Cu(NO3)2·2.5H2O的特殊性，在远离临界场的位置，即使使用精确对角化进行模拟仍可以获得较高的计算精确度，因此在仿真过程中也提供了链长为10的精确对角化算法进行快速计算.

2 仿真平台的实现

结合上述原理，通过Matlab编程及其GUI功能实现了体系的虚拟仿真. 仿真程序分为2部分：1)模拟绝热退磁制冷机的工作流程，让学生对磁热效应有更为直观的认识；2)模拟熵的测量，以此来精确刻画体系的磁热效应.

2.1 绝热退磁制冷

绝热退磁制冷模拟的工作界面如图 2所示，下方控制面板可进行材料选择、工作模式切换和磁感应强度调控. 提供的材料有FAA，GGG和Cu(NO3)2·2.5H2O，工作模式有等温和绝热2种. 右侧参量面板显示了当前温度和磁感应强度，右下方按钮可进行开始测量、保存数据等操作.

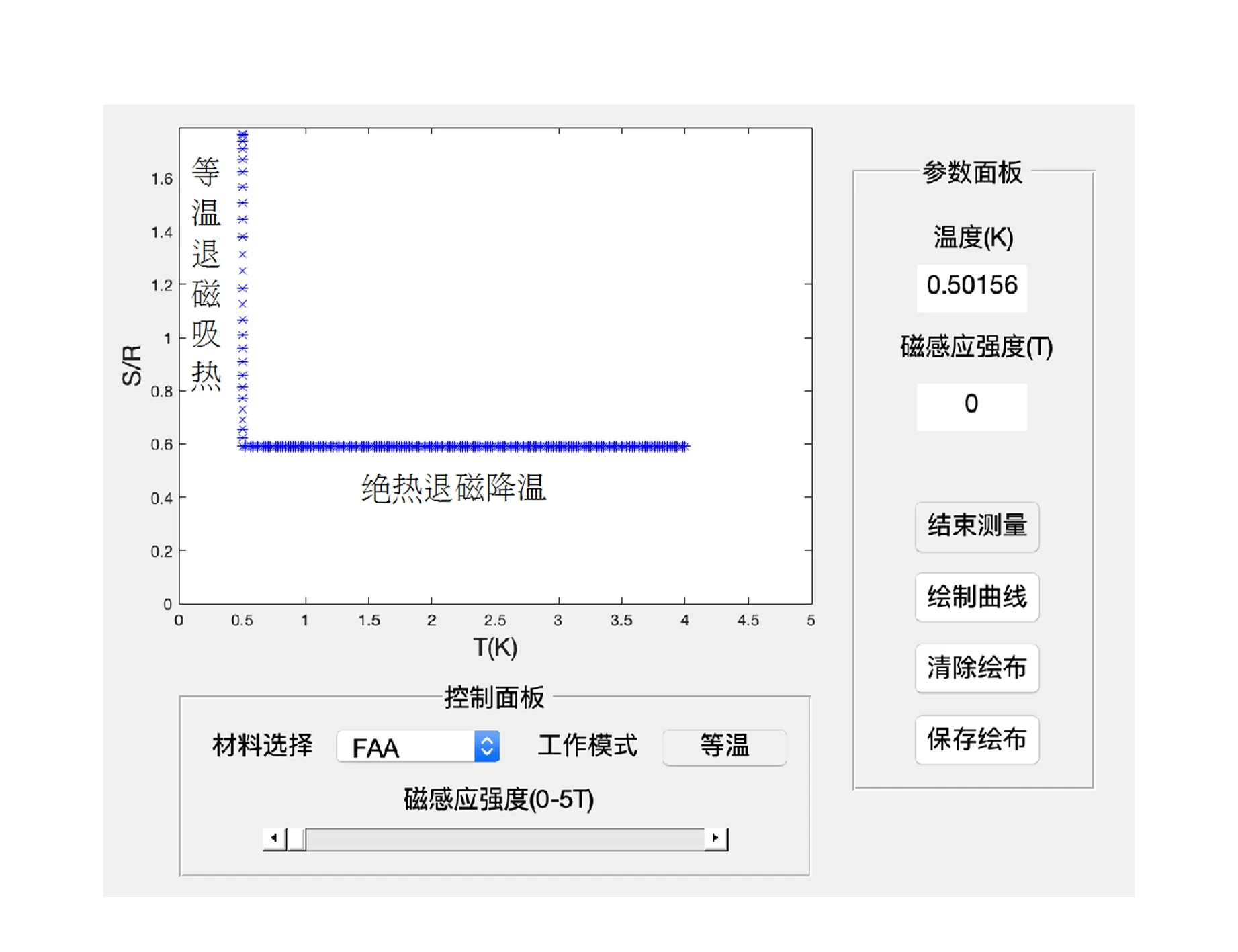
图2 绝热退磁制冷仿真工作流程

在选择好材料，设定好初始温度和磁场后，以“绝热”模式点击“开始测量”，画布上会出现蓝色的“*”，标记体系当前的状态. 通过滑动下方滑块，减小体系当前磁场，可以看到蓝色的“*”在等熵降温. 当达到某个温度后，切换工作模式为“等温”，继续减小磁场，可以看到蓝色的“*”在等温吸热，此时工作介质的熵在提高，直到磁场降至0 T. 在退磁过程中，点击绘制曲线可以获得当前磁感应强度下熵与温度的关系.

2.2 熵曲线测量模拟

熵曲线测量模拟提供了更为精确的数据结果，其工作界面如图3所示，选择好材料和方法后，在参量控制面板中给出相关参量，点击测量即可获得图中熵曲线，点击保存数据即可获得途中点的信息.

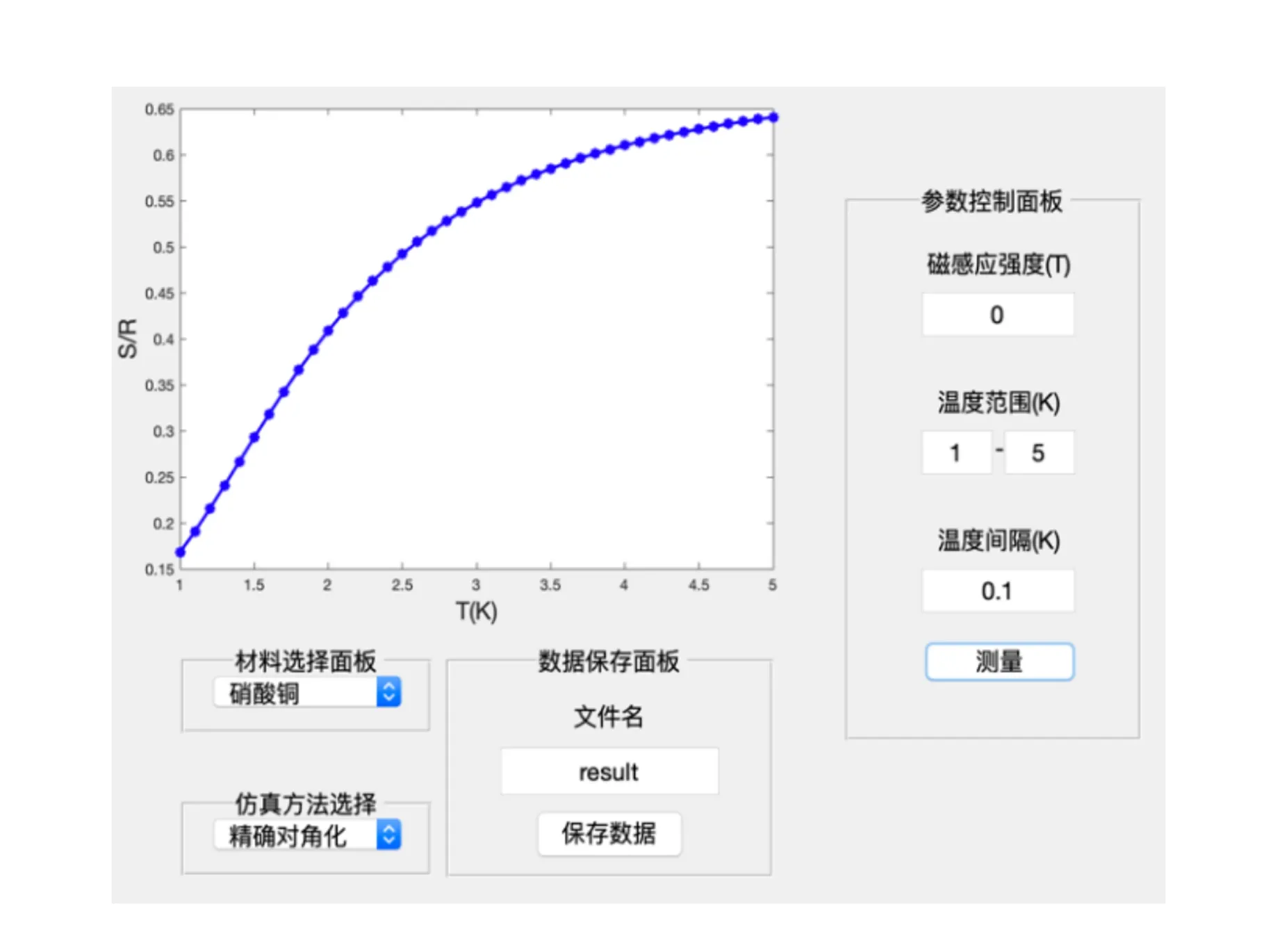
图3 熵曲线测量模拟

3 仿真实验

绝热退磁模拟平台为学生提供了认识磁热效应的直观平台，熵曲线测量模拟部分为精确刻画体系的磁热和反磁热效应提供了数据支持. 利用该仿真平台，学生可直观认识相关材料的磁热效应，并利用熵曲线的数据绘制等熵线，进行更为深入的研究. 下面分别以顺磁盐和Cu(NO3)2·2.5H2O为例进行仿真平台功能的演示.

3.1 绝热温变分析

绝热温变ΔTdd是用来评价工作介质制冷能力的重要指标，决定了降温能到达的最低温度. 下面以顺磁盐FAA和GGG为例来研究此问题. 固定初始磁场为4 T，这是航天器能接受的磁场调控范围；改变其初始温度，分析其绝热温变与初始温度的关系，结果如图 4所示，图中灰色虚线为参考线，其与横轴的截距为绝热降温的终止温度. 考虑到低于奈尔温度后关联会快速建立，近似认为可以达到的最低温度为奈尔温度. 从图4中可以看到，在相同初始温度的条件下，FAA可以在绝热退磁的过程中降到比GGG更低的温度，在2～6 K的初始温度之间都可以绝热降温至奈尔温度附近，这也是FAA被用作绝热退磁制冷机工作介质的原因之一. 而GGG的奈尔温度较高，无法达到较低温度，但其自旋量子数相较于FAA更大，意味其熵变更大，可以吸收更多的热量，因此多用作保护层.

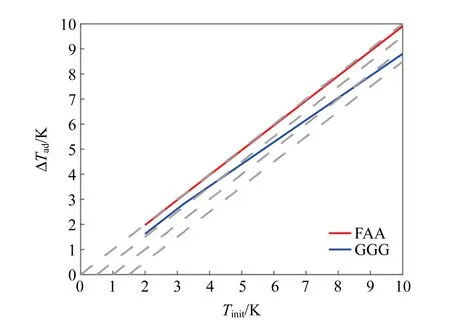
图4 顺磁盐材料绝热温变模拟结果

3.2 等熵线分析

顺磁盐材料的熵曲线分析较为简单，其熵最大的曲线总是在零场处. 而一维自旋链由于量子相变的存在，难以直观地总结出熵曲线的规律，因此需要绘制等熵线对磁热和反磁热效应进行更为充分的分析.

利用熵曲线测量模拟部分，对Cu(NO3)2·2.5H2O在温度范围0.5～5 K、磁感应强度范围0～5 T的熵曲线进行计算，以此来绘制其等熵线. 由于其低温有效模型为海森堡模型，考虑磁场耦合后，体系具有U(1)对称性，此时可以将张量分块，以提高模拟速度. 计算结果如图5所示. 可以看到图中具有2个量子相变点，在这2个量子相变点附近具有磁热和反磁热效应.

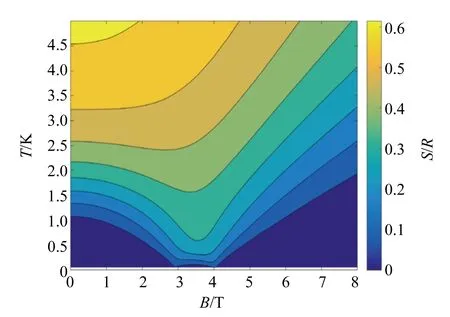
图5 Cu(NO3)2·2.5H2O等熵线模拟结果

从等熵线上可以看到，量子相变点附近的熵被抬高，从熵的定义来看，这意味着体系在相变点附近有较多的许可态. 对于无相互作用系统，在有限场处，体系的基态只能是顺磁的，而零场处，基态却可以是任意的，磁场驱动了体系态密度的变化，从而引发了磁热效应. 对于关联量子材料也可以做类似的分析，当磁场和相互作用达到平衡时，基态附近便会有大量能量相同或相近的态，提高了体系低温下的态密度，从而产生磁热或逆磁热效应.

4 实验教学过程及效果

自编实验讲义，包括背景知识介绍、部分补充知识，以及程序使用方法和相关要求.

顺磁盐的模拟仿真部分让存在于书本的知识与实际应用联系起来. 要求学生利用在热力学与统计物理、量子力学中学到的知识，自行推导无相互作用系统的熵公式，求解有限场与零场下系统的基态. 然后利用仿真系统模拟2种实际材料(FAA和GGG)的熵随着磁场与温度变化的行为，分析其制冷能力.

在关联量子磁体部分的实验教学中，教师先补充一些理论上的背景知识，完成从无相互作用体系到相互作用体系的过渡. 从一维经典伊辛模型出发，即：

(11)

完成背景知识学习后，学生可以模拟不同磁场下的熵曲线，并分析低温下熵随温度变化的行为.当体系基态与第一激发态存在能隙时，熵随温度呈指数下降，下降速度与能隙大小有关.当体系的基态与激发态无能隙时，熵随温度呈代数下降.

通过顺磁部分仿真实验，加深了学生对绝热退磁制冷机工作机制及顺磁体磁热效应成因的理解. 通过关联材料仿真实验，学生对关联量子材料有了深入认识，对量子临界、量子相变等概念有了初步理解，为以后固体理论的学习及相关科研工作奠定了基础.

5 结束语

利用量子统计和量子多体计算，完成了对顺磁盐和一维关联量子材料的热力学精确模拟，建立了磁热效应仿真实验平台. 该平台有效地简化了复杂的实验操作与数据处理，直观展示了FAA，GGG和Cu(NO3)2·2.5H2O在热力学方面对温度及磁场变化的实际响应过程. 在教学方面可以作为学生进一步认识、了解磁热效应和量子磁性等相关知识的平台. 在科研方面，该平台利用的线性张量网络重正化群算法可以为学生解决其他相关问题提供帮助. 除了磁热效应之外，仿真平台还展示了量子相变对体系有限温熵的影响，可以作为学生课外知识的补充. 平台本身也具有良好的延拓性，可以收入新的材料. 未来计划通过自动寻参技术[12]引入更多磁性材料并探究其磁热及逆磁热效应. 同时，将在程序中储存部分预先获得的计算或实验数据，进一步提升程序的流畅性.

致谢:感谢刘鑫阳、于泽昊等同学参与仿真实验，并提供了宝贵的意见；感谢李伟、屈代维和李乔依的有益讨论.