振动流化床内颗粒运动特性的CFD-DEM研究

王晓静 于 雪

（天津大学化工学院）

振动流化床是将振动能量引入普通流化床的新型流化设备，能够强化颗粒运动，改善流化状态，提高气固接触效率，强化传热和传质过程［1］，广泛应用于石油、化工、能源、环保、制药及食品加工等领域的干燥环节。

颗粒在振动流化床内的流化干燥过程涉及气固两相运动，其运动特性一直是人们关注的重点。国内外学者就气泡运动、床层压降、最小流化速度、床层空隙率及多组分床层的混合分离特性等问题开展了广泛的研究。Zhang Y D等研究了振动流化床中床层密度的时空分布规律以及气泡运 动 对 床 层 密 度 波 动 的 影 响［2］；Hashemnia K和Pourandi S定量评估了垂直振动条件下振动频率、振动幅值对流态化质量和流动模式的影响［3］；Cano-Pleite E等利用数字成像技术对竖直振动流化床中的固含率和平均气泡行为进行了实验研究［4］；Wang S等研究了振动幅度、振动频率及流化风速等操作参数对振动流化床流化特性的协同效应［5］。Yang X L等实验研究了表观风速、床层高度、振动强度及流化时间等因素对不同粒径煤分离性能的影响，为干法选煤提供了理论参考［6～8］。

以往的研究中，大多是基于实验手段分析气固两相流的宏观气体动力学特征，而基于微观层面对颗粒运动规律的探讨尚不全面，尤其是对于易损伤物料的干燥过程，既要提高干燥效率，又要降低碰撞强度，减少颗粒损耗。因此，深入分析颗粒的运动机理和碰撞规律，对于改善操作工艺，提高产品质量有重要意义。笔者基于CFDDEM耦合方法，探讨了工业应用卧式振动流化床内，振动参数对颗粒跳动高度、碰撞次数和平均停留时间的影响规律，以期为易损伤物料流化干燥的工业应用提供理论指导。

1 计算模型

CFD-DEM耦合方法中，根据两相之间相互作用影响的显著情况可以分为4类［9］。本研究中当振动流化床干燥机处于正常工作状态时，为避免颗粒碰撞损伤，要求床层只包含单层颗粒，即此时气固两相处于稀相流状态，颗粒运动对于流体流动的影响可以忽略，仅考虑流体流动对颗粒运动的影响，因此该两相流动可以采用CFD-DEM单向耦合方法进行描述，其流体流动方程可以独立于颗粒运动，但颗粒运动方程需要包含颗粒受到的流体作用力。

1.1 颗粒运动方程

采用拉格朗日框架下的离散单元法求解固相运动，其运动由牛顿第二定律控制。颗粒在流体中运动时，受到多个力的作用，通常包含曳力、压力梯度力、浮力、附加质量力、Basset力、Saffman力和Magnus力［10］，本计算中仅考虑对颗粒运动影响较大的曳力和浮力，颗粒运动方程为：

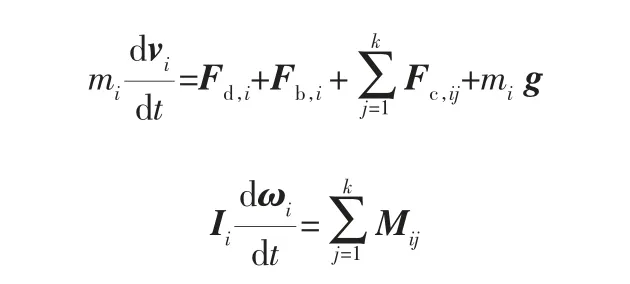
式中 Fb，i——颗粒i受到的浮力；

Fc，ij——颗粒i和颗粒j碰撞产生的接触力［11］；

Fd，i——颗粒i受到的曳力；

g——重力加速度；

Ii——颗粒i的转动惯量；

k——与颗粒i相接触的颗粒和壁面单元的总数；

Mij——颗粒i和颗粒j碰撞产生的力矩［11］；

mi——颗粒i的质量；

t——时间；

vi——颗粒i的线速度；

ωi——颗粒i的角速度。

1.2 流体控制方程

在CFD-DEM耦合方法中，流体采用连续介质假定，其运动控制方程为Navier-Stokes方程：

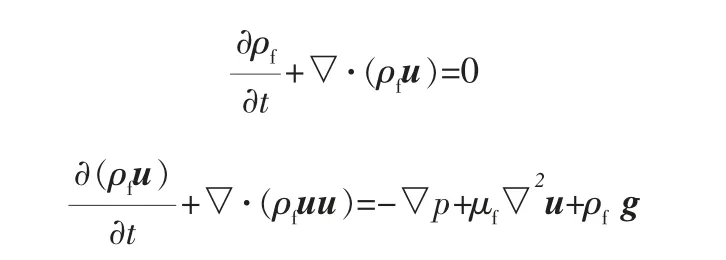
式中 p——流体压力；

u——流体速度矢量；

ρf——流体密度；

μf——流体动力粘度。

1.3 流体作用力计算模型

单个颗粒在流体中受到的曳力与颗粒和流体之间的速度差成正比，即：

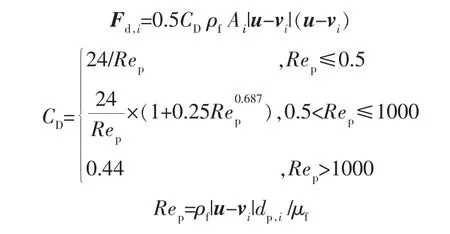
式中 Ai——与实际颗粒体积相等的球形颗粒投影面积；

CD——阻力系数；

dp，i——颗粒i的等体积当量直径；

Rep——颗粒的雷诺数。

颗粒受到浮力的计算式为：

Fb，i=ρfgVp，i

式中 Vp，i——颗粒i的体积。

2 数值模拟

2.1 振动流化床模型

卧式振动流化床的结构如图1所示，其长度为3 660 mm，高度为1 578 mm，由于该结构具有平移周期性且气速沿宽度方向变化较小，宽度取实际值的1/5即62 mm；气体分布板的尺寸为3 130 mm×62 mm×5 mm，开孔呈正三角形方式排布，开孔直径为0.8 mm，孔间距为7 mm。

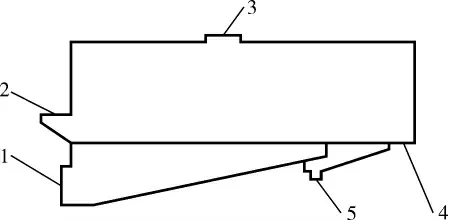
图1 卧式振动流化床结构示意图

2.2 颗粒模型

在离散元模拟软件中建立3种非球形颗粒模型，其相关参数见表1。

表1 非球形颗粒模型参数

2.3 求解设置

求解连续相时，采用稳态求解方法，湍流模型选用k-ε标准模型，气体进口设为速度入口，颗粒进口设为速度入口且速度为0，气体出口和颗粒出口均设为压力出口，前后壁面设为周期性边界条件，其余壁面设为无滑移壁面。

求解离散相时，设置气体分布板的振动参数，沿宽度方向设为周期性边界条件，每种颗粒的投放量为35个/s，计算时间步长为2×10-5s。

气体、颗粒和床体的物性参数如下：

气体密度 0.972 kg/m3

气体粘度 0.021 5 mPa·s

颗粒密度 1 700 kg/m3

颗粒泊松比 0.48

颗粒剪切模量 10 MPa

床体密度 7 980 kg/m3

床体泊松比 0.30

床体剪切模量 79 GPa

颗粒与颗粒、颗粒与床体的接触参数分别为：

颗粒-颗粒静摩擦系数 0.80

颗粒-颗粒动摩擦系数 0.10

颗粒-颗粒恢复系数 0.45

颗粒-床体静摩擦系数 0.30

颗粒-床体动摩擦系数 0.05

颗粒-床体恢复系数 0.50

2.4 模拟工况

模拟工况参数见表2。

表2 模拟工况参数

表2中振动强度K的计算式为：

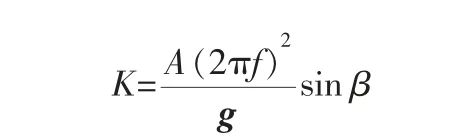
式中 A——振动幅值，mm；

f——振动频率，Hz；

β——振动角度，即颗粒运动方向和激振力方向的夹角，（°）。

3 模拟结果分析

3.1 颗粒跳动高度

由于所研究的物料受到剧烈碰撞时容易掉渣，因此在干燥过程中需要尽量避免颗粒与分布板之间发生较为剧烈的碰撞，而颗粒与分布板之间的碰撞强度可由颗粒的跳动高度间接反映得到。振动流化床处于稳定运行阶段时，不同振动强度下颗粒和分布板的高度变化如图2所示。

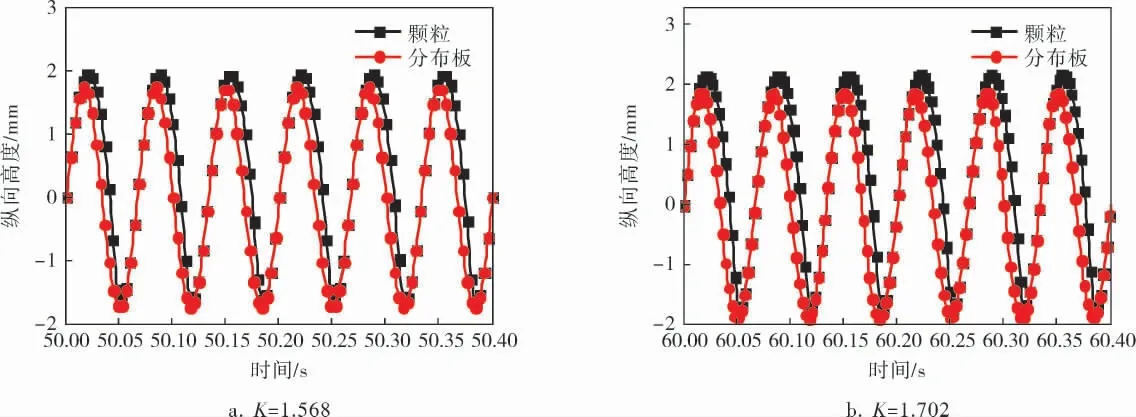
图2 不同振动强度下颗粒和分布板的高度变化

由图2可以看出，颗粒在高度方向上近似做正弦运动，其运动频率与分布板振动频率一致，但颗粒运动要滞后于分布板的运动，在一个运动周期内，按颗粒高度位置的正负值将颗粒运动分为“上升”阶段和“下降”阶段。颗粒在“上升”阶段的运动时间和运动幅值明显大于“下降”阶段，且随着振动强度的增加，“上升”阶段所占时间和运动幅值逐渐增加。颗粒运动曲线和分布板运动曲线的交点代表两者的碰撞点，随着振动强度的增加，颗粒与分布板的碰撞点逐渐后移。

分析颗粒和分布板的运动过程发现，颗粒和分布板碰撞后，颗粒的加速度大于分布板的加速度，因而颗粒的上升高度更高，从最高点下落至初始位置的时间也更长，因此其运动要滞后于分布板的运动；在颗粒“下降”阶段，当颗粒还未下落至最低点时，分布板已从最低点向上运动，于是颗粒的下落受到分布板的阻挡，因此其“下降”阶段的幅值和时间要小于“上升”阶段的。而当振动强度增加时，颗粒受到的激振力随之增大，获得的动能和上升高度也随之增加，进而颗粒运动滞后于分布板运动的时间增长，即出现颗粒“上升”和“下降”两个阶段的差异不断增大的现象。

基于单因素变量法分析振动频率、振动幅值和振动角度对颗粒跳动高度的影响规律如图3所示。在高度方向上，颗粒受到的激振力分量为激振力与振动角度正弦值的乘积，因此不论是增大振动频率、振动幅值还是振动角度，本质上均是增大了高度方向上的激振力分量，因而颗粒的跳动高度随之增加，且均沿线性规律变化。

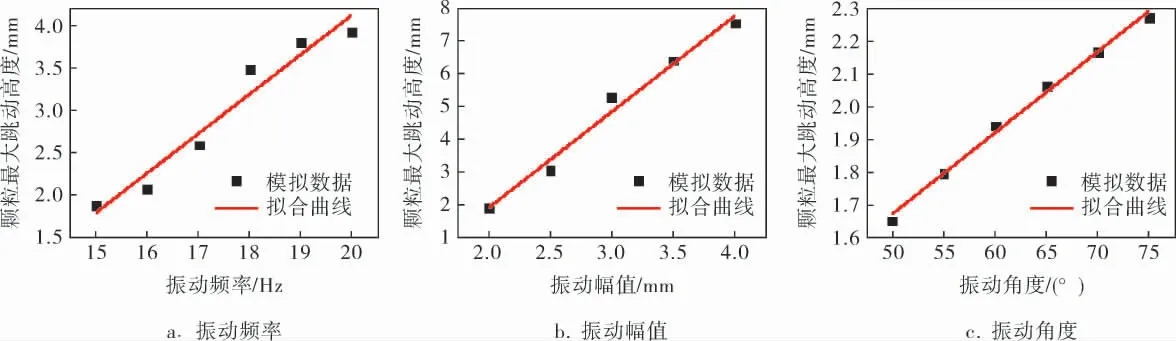
图3 振动参数对颗粒最大跳动高度的影响规律

3.2 颗粒碰撞次数

在振动流化床中，颗粒运动的安全性除了与颗粒碰撞强度有关，还应考虑颗粒在干燥期间经历的碰撞次数。不同振动强度下，颗粒碰撞的总次数和颗粒仅与分布板碰撞的次数随时间的变化规律如图4所示。

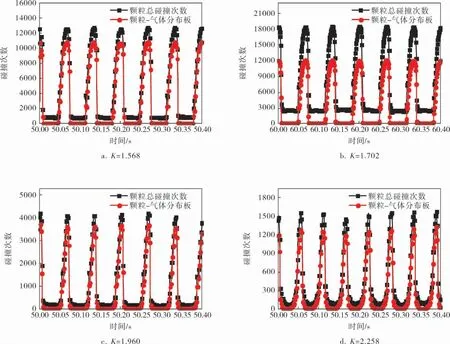
图4 碰撞次数随时间的变化规律

从图4可以看出，颗粒碰撞的总次数呈周期性变化，其变化频率与分布板振动频率一致，且颗粒与分布板碰撞的次数在总碰撞次数中占主导地位，颗粒与颗粒碰撞的次数和颗粒与床体其他部位碰撞的次数所占比例较小。图4中碰撞次数由水平段上升至峰值后下降至水平段的部分，其对应的时间段表示颗粒与分布板接触的时间，可以发现随着振动强度的增大，颗粒与分布板碰撞的时刻后移，进而颗粒与分布板接触的时间段逐渐减小；相应地，图4中曲线的水平段对应颗粒离开分布板的时间段，随着振动强度的增大，颗粒离开分布板的时间增长，但当振动强度达到一定值时，颗粒在竖直方向上的运动一致性降低，即颗粒接触和离开分布板的时间存在差异，从而导致碰撞次数接近于零的时间段减小，即图4中曲线的水平段逐渐变为圆弧段。

此外，图4表明在颗粒运动的一个周期内，颗粒的碰撞次数峰值随振动强度先增大后减少，由此可见，颗粒的碰撞次数变化规律较为复杂。振动频率、振动幅值和振动角度对颗粒碰撞次数的影响规律如图5所示。

由图5可以看出，颗粒数量与碰撞总次数随振动参数呈现较为一致的变化规律，由此表明，在进料量一定的条件下，床内颗粒数量是影响颗粒碰撞总次数的主要原因。分析颗粒受力得到，颗粒在水平方向上运动的初速度取决于激振力的水平分量，其大小为激振力与振动角度余弦值的乘积，因此当增大振动频率或振动幅值时，激振力水平分量增大，振动流化床输送颗粒的效率随之增加，床内颗粒数量相应减小，导致颗粒碰撞总次数下降，当振动频率达到18 Hz或振动幅值达到3.0 mm时，颗粒碰撞总次数较为稳定；当增大振动角度时，颗粒在水平方向上受到的激振力减小，因而振动流化床输送颗粒的效率降低，床内颗粒数量明显增加，颗粒碰撞总次数随之增大，且随着振动角度的增大，水平激振力的下降速率增大，从而颗粒碰撞次数的变化速率随之增大。

图5 振动参数对颗粒碰撞次数的影响规律

3.3 颗粒停留时间

在干燥介质一定的条件下，颗粒在流化床内的停留时间决定了颗粒的最终干燥效果，研究不同振动参数对停留时间的影响规律，对于优化颗粒干燥工艺、提高干燥效率有重要意义。

在干燥介质一定的条件下，振动频率、振动幅值和振动角度对颗粒停留时间的影响规律如图6所示。

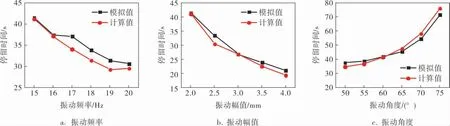
图6 振动参数对颗粒停留时间的影响规律

由图6可以看出，随着振动频率和振动幅值的增大，颗粒停留时间呈线性规律缩短，拟合数据得到颗粒停留时间关于振动频率和振动幅值的表达式分别为T=-2.16f+73.07和T=-10.07A+59.59；振动角度对颗粒停留时间的影响规律较为显著，随着振动角度的增大，颗粒停留时间逐渐延长，二者呈二次函数关系，其表达式为T=148.61-4.66β+0.048β2。如前所述，当增大振动频率和振动幅值，或者减小振动角度时，均增大了水平激振力，进而颗粒的水平运动速度提高，颗粒停留时间相应缩短。为进一步验证数值模拟结果的准确性，采用文献［12］中的经验公式求解不同振动条件下的停留时间，发现两种方法得到的结果具有较好的一致性，平均误差约为5%，误差值在允许范围之内，模拟结果合理有效。

4 结论

4.1 颗粒跳动高度近似呈正弦规律变化，其变化频率与分布板振动频率一致，在高度方向上颗粒运动要滞后于分布板的运动，随着振动强度的增加，颗粒床层和气体分布板的碰撞点逐渐后移，颗粒在“上升”、“下降”阶段的运动幅值和运动时间的差异逐渐增大。颗粒的跳动高度幅值分别随着振动频率、振动幅值和振动角度的增大而沿线性规律增大。

4.2 颗粒与分布板之间的碰撞次数在颗粒经历的总碰撞次数中占主导地位，颗粒床层的碰撞次数与床内颗粒数量有关，当增大振动频率和振动幅值或减小振动角度时，床内颗粒数量减少，碰撞次数随之降低。

4.3 随着振动频率和振动幅值的增大，颗粒停留时间呈线性规律缩短；随着振动角度的增大，颗粒停留时间呈二次函数关系逐渐延长。