基于田口稳健设计的跨座式单轨车辆悬挂系统多参数优化

赵树恩，聂小芮，陈文斌

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

城市轨道交通作为一种新型的交通制式，在优化城市布局、降低交通压力方面有着不可替代的影响。其中，跨座式单轨车辆系统作为一种特殊形式的城市轨道交通系统，具有较大的运载能力、较强的爬坡能力及较小的转弯半径，十分适合于地形复杂、地铁修建难度大的城市，赢得了许多城市的青睐。但是其较小的转弯半径和轨道梁不平度等因素也使其运行稳定性和乘客乘坐舒适性降低，带来了新的问题有待解决。

中央悬挂系统是影响单轨车辆运行平稳性的主要因素，众多专家学者对单轨车辆中央悬挂系统进行了深入研究。杜子学等[1]在SIMPACK软件中建立了单轴式单轨车辆多体动力学模型，对空气弹簧各参数进行了灵敏度分析。基于改进后的遗传算法，对悬挂参数进行了多目标优化，改善了单轨车辆的动力学性能；谢毅等[2]针对悬挂式单轨车辆-轨道系统，建立了60自由度的动力学模型，以车体和摇枕为主要研究对象，分析了不同减振装置参数对车体横向偏角的影响，探究了其变化规律；唐飞等[3]针对悬挂式单轨车辆在曲线行驶工况下车体侧滚角较大的问题，基于mode FRONTIER软件对单轨车辆车体侧滚角的影响因素进行了灵敏度分析，并利用NSGA-II遗传算法进行了参数优化，有效的控制了单轨车辆在通过曲线路段时的侧滚；陈志辉等[4]基于多体动力学理论，研究了悬挂式单轨车辆在不同载荷条件下的运行平稳性的变化规律，并结合现场力学试验，对悬挂参数进行了优化。

通过分析比较发现上述研究方法虽然改善了单轨车辆的动力学性能，但大多数针对于悬挂系统的参数优化仍属于单目标优化，得到的优化结果仅限于单一参数，故存在较大的局限性。多目标稳健优化的目的在于兼顾各项外界干扰因素的同时，合理匹配单轨车辆各悬挂参数。基于稳健试验设计的方法，选择跨座式单轨车辆悬挂系统多个关键零部件参数进行正交试验和信噪比分析，综合考虑车辆纵横向平稳性指标，完成多参数的稳健性优化匹配，以提高车辆运行品质。

1 单轨车辆系统动力学模型

1.1 转向架结构及多体动力学模型

跨座式单轨车辆-轨道系统主要由车体、转向架和轨道梁组成。典型的单轨车辆转向架如图1。其主要由转向架构架、中央悬挂系统、轮对、基础制动装置及牵引传动装置等组成。其中，对单轨车辆运行平稳性影响最大的是中央悬挂系统，其安装在车体和构架之间，为车辆提供第二级减振，主要作用是传递车体与转向架之间的垂向、横向和纵向力，其主要构成部分有空气弹簧、油压减振器、牵引橡胶堆、横向缓冲器、中心销及中心销座等[5]。

当单轨车辆在轨道梁上运行时，由于轨面不平度、侧风、轨道超高、载荷变化等众多激励的影响，振动由轨道梁经各个轮对组成的一系悬挂传递到中央悬挂系统组成的二系悬挂，最终传递到车体，影响单轨车辆的运行平稳性。同时，由于二系悬挂的刚度远远小于一系悬挂，故可以将轮对和转向架看作刚体，直接受到车体的约束。因此，单轨车辆的稳定性主要由中央悬挂系统参数决定，优化中央悬挂系统各零部件参数对提高单轨车辆的运行平稳性具有重要意义。

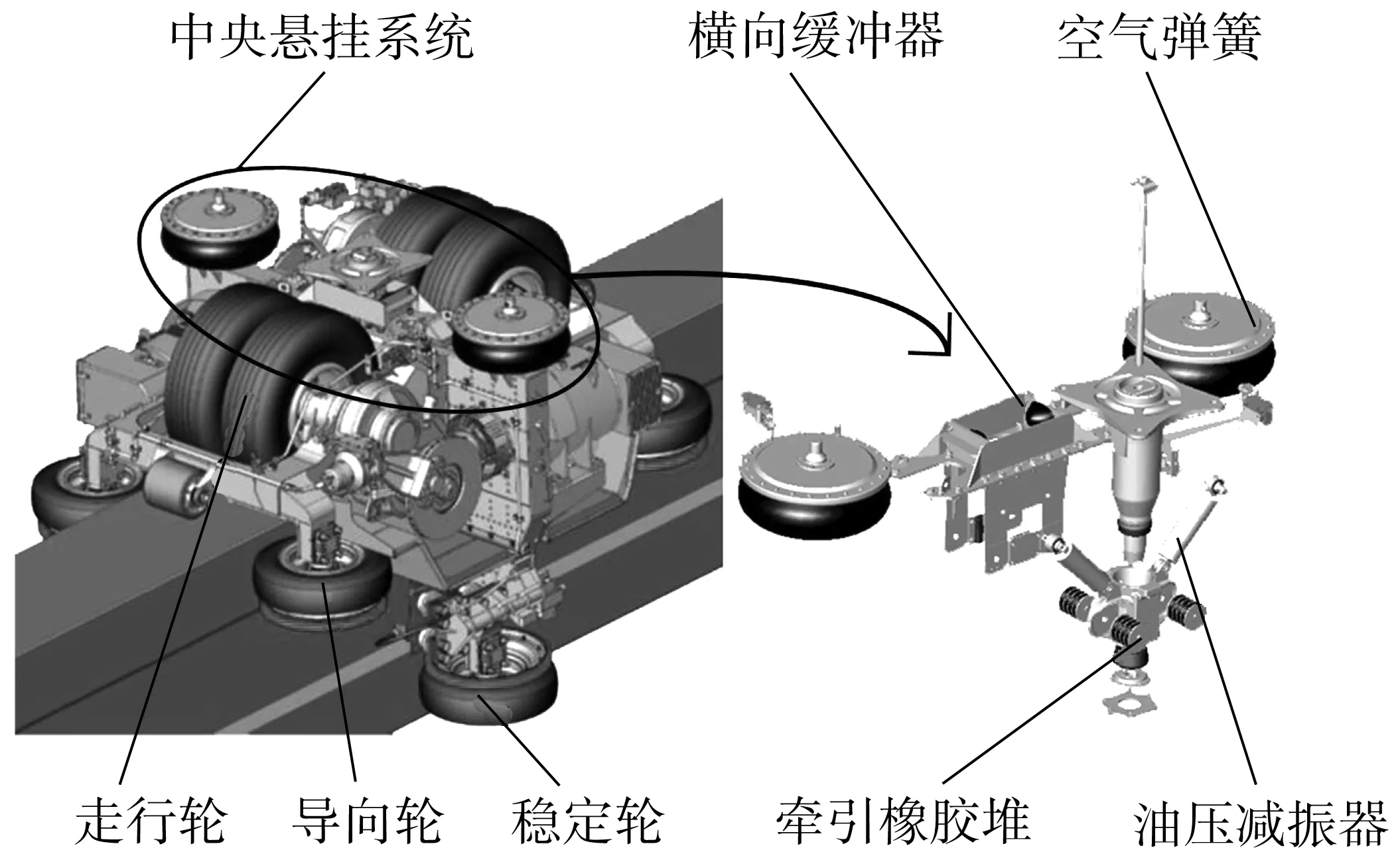
图1 转向架结构Fig. 1 Bogie structure diagram

1.2 整车多体动力学模型

跨座式单轨车辆-轨道系统包括众多部件及非线性元件，是一个复杂且具有多自由度的非线性系统。在具体分析之前，需将其简化为由刚体、力元、铰等要素组合而成的车辆系统动力学模型。以重庆轨道3号线的单轨车辆为研究对象，基于多体动力学理论，对车辆结构作合理的简化，建立其拓扑构型关系，如图2。图2中，Mc、Mb分别为车体和构架的质量；ksl为空气弹簧的横向刚度；csl为空气弹簧的横向阻尼；ksv为空气弹簧的垂向刚度；csv为空气弹簧的垂向阻尼；c0为油压减振器阻尼。

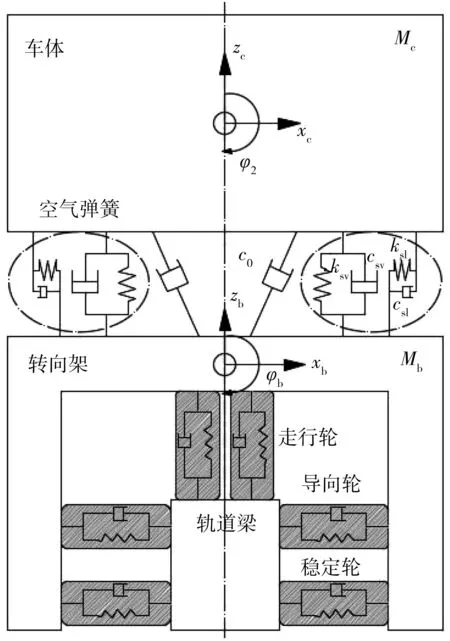
图2 单轨车辆拓扑结构Fig. 2 Topological structure diagram of monorail vehicle

在多体动力学软件中建立单轨车辆的非线性动力学模型如图3，该单轨车辆模型主要由1个车体、2个转向架组成，车体和转向架构架之间安装有空气弹簧、油压减振器、横向止挡等衰减车体与转向架之间的振动。每个转向架上均设置有两对走行轮轮对、两对导向轮轮对及一对稳定轮轮对,走行轮、导向轮、稳定轮均采用橡胶轮胎，在传递整车动力的同时起到一系悬挂的作用，整车不设一系悬挂，采用此模型进行多体动力学分析。

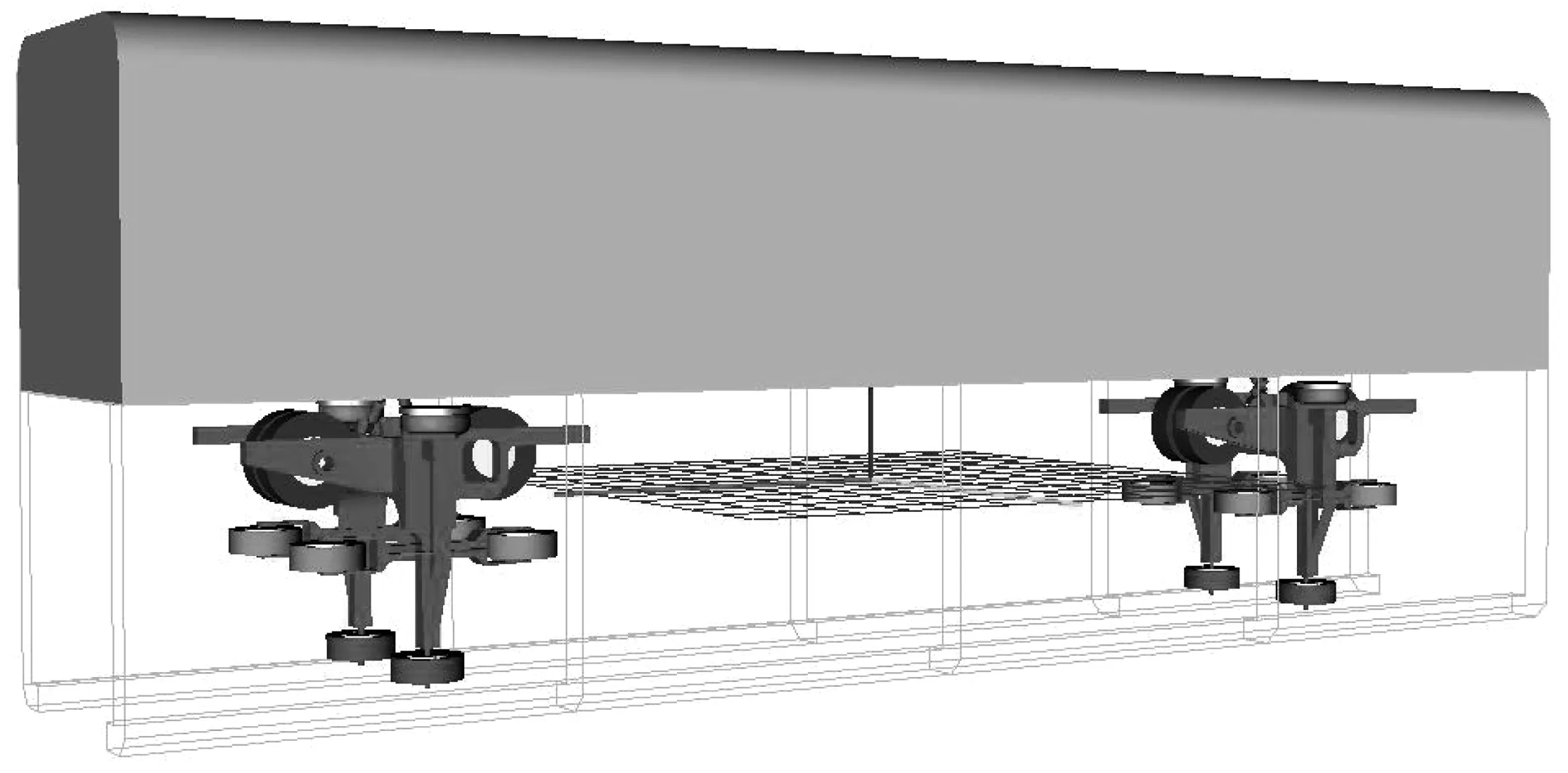
图3 单轨车辆多体动力学模型Fig. 3 Multi-body dynamics model of monorail vehicle

1.3 模型的仿真与验证

参考GB504528—2008《跨座式单轨交通设计规范》表4.1.3中规定的跨座式单轨车辆参数，确定仿真模型各主要参数如表1。

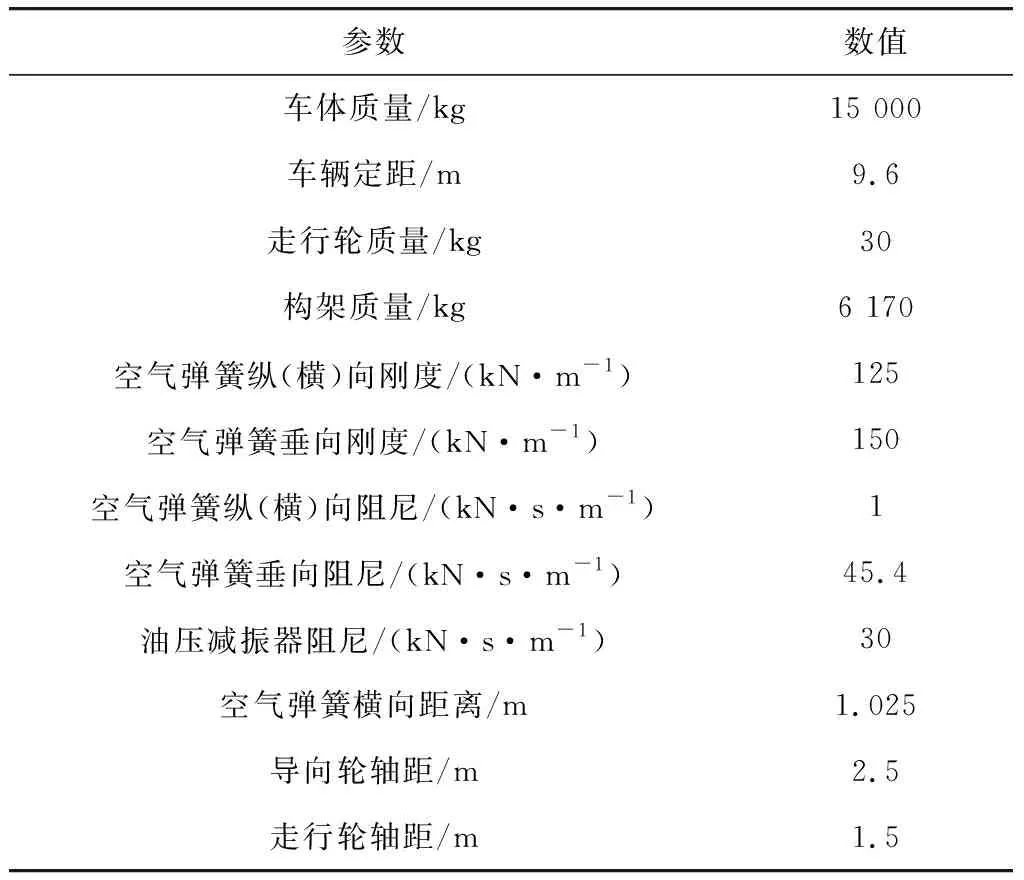
表1 跨座式单轨车辆主要技术参数Table 1 Main technical perameters of straddle monorail vehicles

为验证所建立的模型的正确性，在直线轨道工况下，采用美国六级轨道谱对单轨车辆轨道梁不平顺进行模拟，设置车速分别为10、20、30、40 km/h，依次进行仿真分析。分别提取单轨车辆横、垂向加速度，与文献[6]中实测的重庆跨座式单轨车辆加速度数据进行对比，如表2。从表2中可以看出，实测数据与仿真数据相差不大，仿真模型具有一定的可靠性。

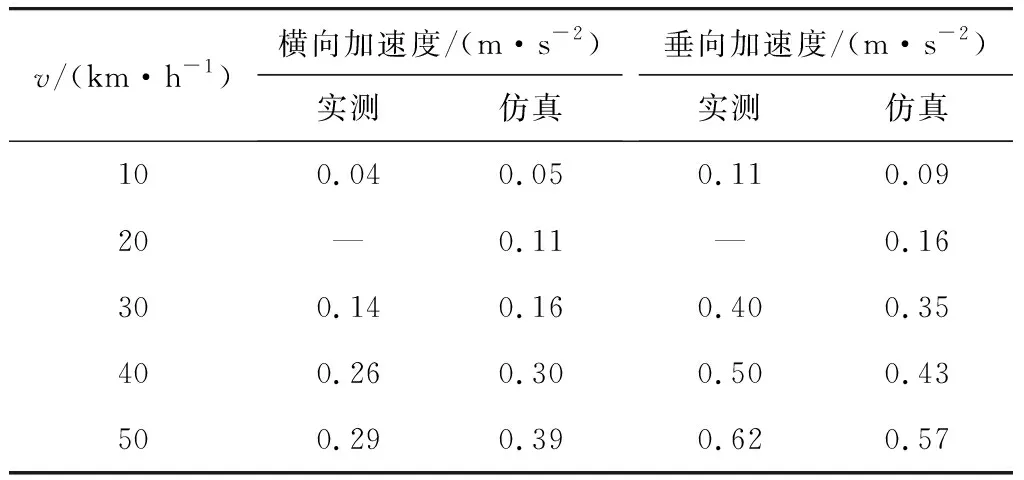
表2 仿真数据与实测数据对比Table 2 Comparison of the simulated data and the measured data

2 悬挂参数多目标优化匹配

2.1 田口试验设计方法

稳健性是指设计指标对外界噪声因素变化的不敏感性。稳健试验设计法可以高效的进行产品设计，其流程分为3个部分，分别为系统设计、参数设计和容差设计。其中最关键的部分是以正交试验设计(design of experiment，DOE)为基本方法的参数设计方法，其优化流程如图4[7]。

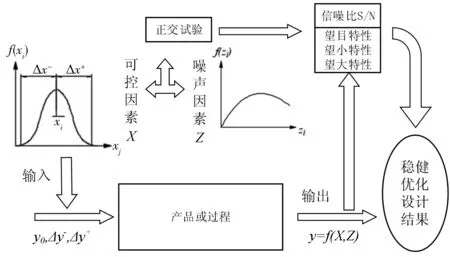
图4 田口试验设计流程Fig. 4 Taguchi test design flow chart

由图4看出，田口稳健性试验设计将影响产品质量的因素分为可控因素和噪声因素两种，并将其作为正交试验的输入。经过不断地产品或过程的试验和信噪比分析，最终得到稳健优化设计结果。稳健设计的主要分析工具是信噪比(signal-noise Ratio，S/N)，S/N的值越大，则设计的产品质量特性越稳定，产品的质量特性越好。

在稳健试验设计中，产品的质量特性分为望目特性、望小特性和望大特性[8]。具体推导过程如下：假设产品的输出目标特性y具有正态分布N(μy,σy)的特性，若想要得到较大的信噪比，需要取μ2+σ2越小越好，即取：

(1)

式中：μ2+σ2为y2的期望值，可由E(y2)的无偏估计来代替，即：

(2)

取对数，即得到望小特性的信噪比公式为：

(3)

式中：yi为第i次试验的目标函数值；n为指标的数量，下同。

同理，可得到望目特性的信噪比公式为：

(4)

望大特性的信噪比公式为：

(5)

通过计算其信噪比确定最终的稳健性优化结果。希望单轨车辆稳定性指标较小，以得到好的运行稳定性和乘坐舒适性，因此采用望小特性的信噪比计算公式。

2.2 稳健优化设计方法

稳健优化设计方法是通过减小不确定因素在成品设计和生产过程中对质量特性的影响，实现提高产品质量稳定性的目的。稳健优化设计通过控制质量特性函数的起伏和震荡，使其实际值尽量接近目标值，降低对外界干扰的敏感性，使得能够得到符合要求的均值和最小化方差。找到一个符合设计要求的参数波动区间是稳健性优化设计的核心目的，因此需要充分考虑外界因素和设计变量的影响，得到考虑目标均值和均方差的典型稳健优化函数如下：

(6)

式中：x为设计变量；Gj为约束函数；j为约束函数的个数；xL、xU分别为设计变量的下限和上限。

稳健试验设计法运用到单轨车辆悬挂参数多目标优化中，使车辆的各项悬挂参数同时得到优化，并使得车辆的悬挂系统具有稳健性，即在各种外界因素影响下，单轨车辆纵横向平稳性指标变化幅度更小。稳健性优化的过程可表述为[9]：

1)确定目标函数：优化目的为改善单轨车辆的运行平稳性指标，文中目标函数即为纵横向加权运行平稳性指标。

2)进行正交试验：确定可控因素、噪声因素及其水平，建立正交试验表，分别进行仿真试验，得出仿真试验结果。

3)稳健性和极差分析：将每次仿真试验结果代入望小特性的信噪比计算公式，得到优化后的单轨车辆悬挂系统各零部件参数并进行稳健性和极差分析。

4)结果验证：对优化前后的车辆运行平稳性指标进行对比分析，以评价其是否得到改善。

2.3 单轨车辆运行平稳性评价指标

目前国内外尚未建立完善的跨座式单轨车辆运行平稳性评价体系，因此，笔者采用铁道车辆的斯贝林平稳性指标来评价单轨车辆的运行平稳性，其计算公式为[10]：

(7)

式中：W为平稳性指标；A为车体振动加速度；f为振动频率，Hz;F(f)为频率修正系数。

式(7)的平稳性指标评价方法仅包含车辆振动的单一频率成分，但事实上单轨车辆的振动包含多个频率成分。因此，计算实际车辆的运行平稳性指标时，要求出各个频率范围内的车辆振幅，分别计算平稳性指标，从而求出单轨车辆整个频率范围内的平稳性等级[11]。当含有h个频率成分时，平稳性指标的计算公式为：

(8)

式中：h为整个频率波段的频率成分总数。

2.4 单轨车辆平稳性影响因素分析

为了对单轨车辆系统稳定性进行针对性优化，应对单轨车辆平稳性的影响因素进行分析。笔者采取变化系数法分析系统各零部件参数对单轨车辆纵横向平稳性指标的影响，将悬挂零部件参数的原始值乘以变化系数得到试验值，变化系数范围从0.5～1.5，各悬挂零部件参数对单轨车辆纵横向平稳性指标的影响趋势如图5～图6。

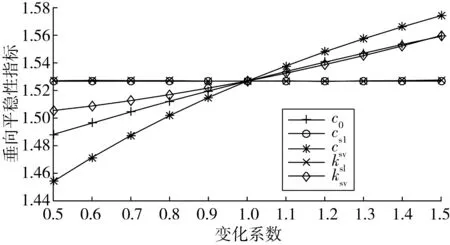
图5 垂向平稳性指标Fig. 5 Vertical stability index

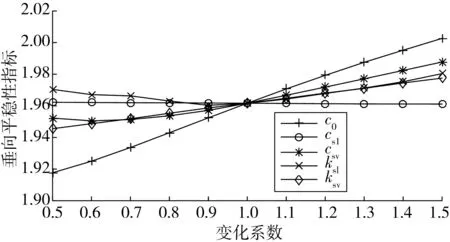
图6 横向平稳性指标Fig. 6 Horizontal stability index

由图5～图6可见，对于垂向平稳性指标影响较大的因素依次为：空气弹簧垂向阻尼csv、油压减振器阻尼c0、空气弹簧垂向刚度ksv。对于横向平稳性影响较大的因素依次为：油压减振器阻尼c0、空气弹簧垂向阻尼csv、空气弹簧垂向刚度ksv。因此，综合分析试验结果，选取油压减振器阻尼c0、空气弹簧垂向阻尼csv以及空气弹簧垂向刚度ksv作为关键参数进行多目标优化。

2.5 正交试验设计

由2.4节可知，跨座式单轨车辆中央悬挂系统的主要参数有空气弹簧垂向刚度ksv、空气弹簧垂向阻尼csv以及油压减振器阻尼c0。

为了确定单轨车辆最优悬挂参数，需要进行正交试验设计。首先确定可控因子和噪声因子的水平个数，选择悬挂参数初始值上下浮动20%的5个值作为5个水平进行试验。可控因子的水平值如表3。考虑可控因子及其水平的个数，根据正交设计相关理论，选取L25(35)正交表进行实验。

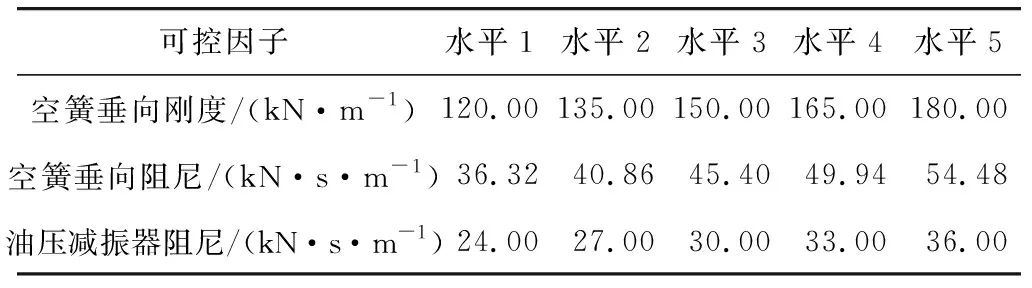
表3 可控因子水平Table 3 Controllable factor levels

基于单轨车辆实际运行状况，分析影响单轨车辆运行平稳性的因素，选取运行速度、载荷条件和弯道半径为3个噪声因子，根据单轨车辆常规运行状态确定其水平的选取，如表4。考虑噪声因子及其水平的个数，将L9(33)正交表作为外表。

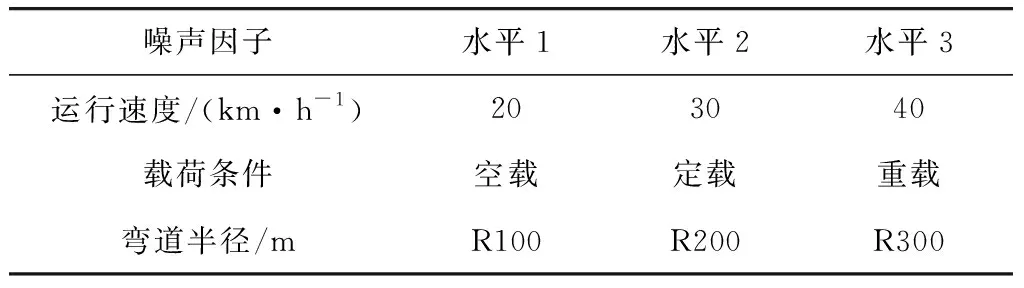
表4 噪声因子水平Table 4 Noise factor level

其中，根据GB50458—2008《跨座式单轨交通设计规范》规定，跨座式单轨车辆中车定员人数为165人，超员人数为230人，每位乘客按体重50 kg计算。

2.6 田口正交试验

根据正交表进行试验，运行UM仿真，计算出各次试验在3个噪声因子影响下的纵横向平稳性指标。试验完成后，根据望小特性的信噪比计算公式，计算出实验结果的信噪比。

为确定最终的多目标优化结果，综合考虑横向平稳性指标和垂向平稳性指标，对2个目标的的信噪比进行加权处理作为最终信噪比[12]。设横向平稳性指标信噪比和垂向平稳性指标信噪比各次试验结果分别为n1、n2，则定义约束系统的评价函数为式(9)，即加权信噪比指标：

(9)

有相关研究表明，人体对于横向振动的敏感程度相比于纵向振动的敏感程度大[13]。因此，横向平稳性指标的权重系数应比纵向平稳性指标的大。

3 试验结果分析

3.1 田口正交试验结果分析

为了确定各噪声因素对单轨车辆平稳性指标的影响，对试验结果进行极差分析。极差分析具有简单直接的特点，通过极差分析可以判断各噪声因子对于单轨车辆平稳性的影响程度[14]。

(10)

式中：Ki是指水平i的总体偏差平均值。

由式(10)计算得到各噪声因子的影响趋势如表5。由表5可知，单轨车辆运行平稳性随运行速度的增加而变差，随载荷水平的增加而变好，

随弯道半径的增加而变差。各噪声因子对于单轨车辆运行平稳性的影响从大到小依次为：运行速度、载荷水平、弯道半径。

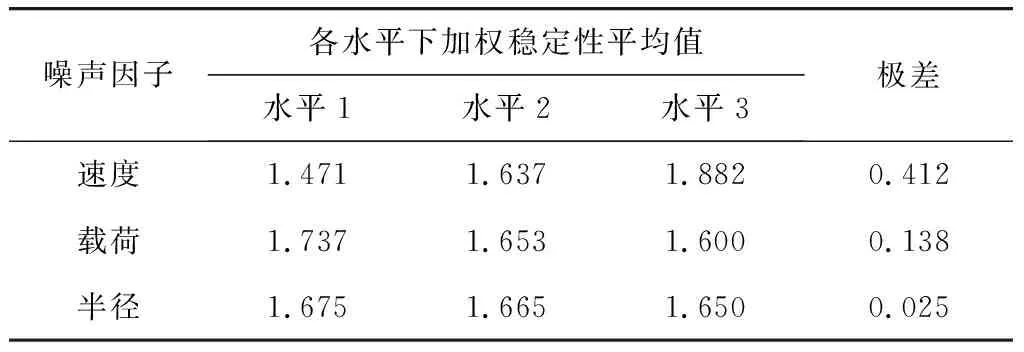
表5 噪声因子分析Table 5 Noise factor analysis

3.2 稳健性优化结果分析

各可控因素的信噪比主效应图如图7～图8。由图可知，空气弹簧垂向刚度ksv、垂向阻尼csv以及油压减振器的阻尼c0的信噪比参数随着因子水平的增加而减小，而均值随着各参数水平的增大而增大。因此，可以得出跨座式单轨车辆悬挂参数在可控范围内的最佳参数匹配如表6。

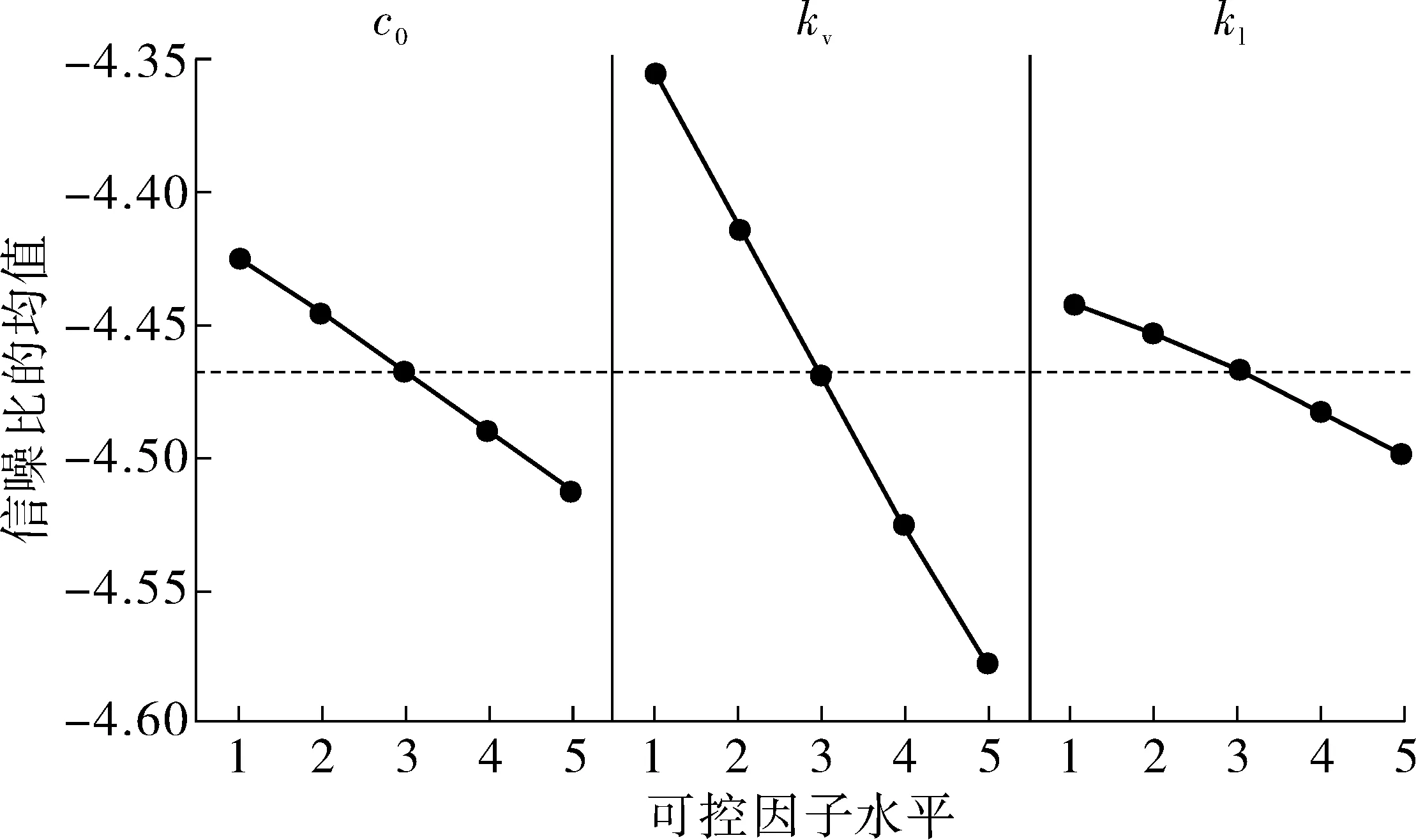
图7 信噪比主效应Fig. 7 SNR main effect

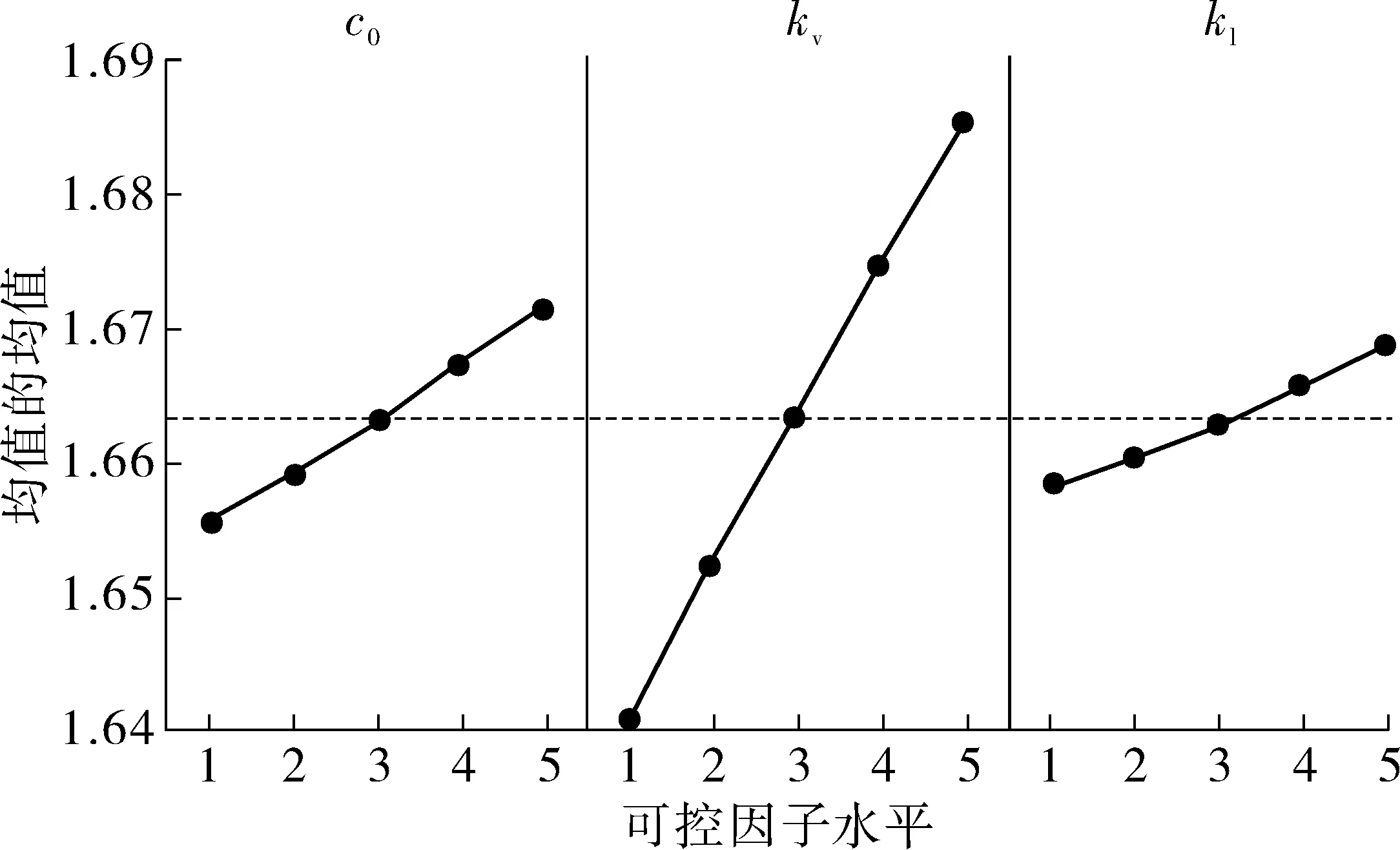
图8 均值主效应Fig. 8 Mean main effect

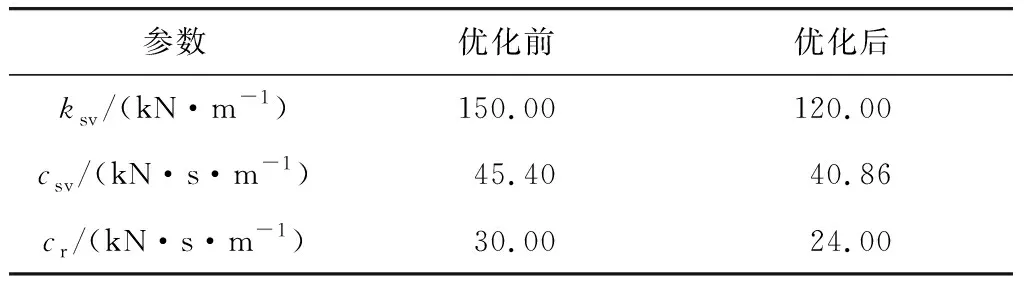
表6 最优试验中的悬挂参数Table 6 Suspension parameters in the optimal test

3.3 优化结果验证

对稳健优化前后单轨车辆在不同噪声因子组合工况下进行仿真分析，经过计算得到仿真结果如表7。由表7可知，在9种仿真工况下，车辆的横向平稳性指标和垂向平稳性指标都有不同程度的提高，同时车辆纵横向平稳性均值均有所减小，信噪比增大，表明单轨车辆悬架系统稳健性有所提高。

表7 优化前后仿真结果Table 7 Simulation results before and after optimization

根据表5噪声因子极差分析结果，运行速度对单轨平稳性的影响最大，因此，在不同运行速度条件下对优化前后单轨车辆运行平稳性进行仿真分析，仿真结果如图9～图10。由图可见，优化后单轨车辆在不同运行速度条件下垂向平稳性指标显著提升，横向平稳性指标也有一定改善。综上所述，笔者对跨座式单轨车辆悬挂系统的参数优化是有效的。

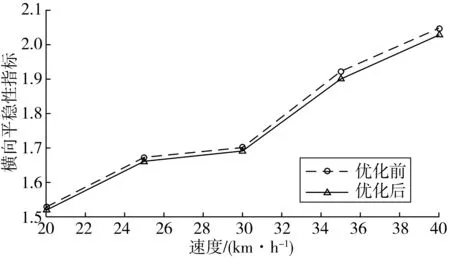
图9 横向平稳性指标Fig. 9 Horizontal stability index

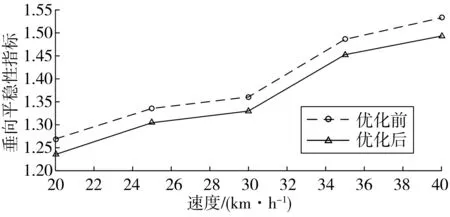
图10 垂向平稳性指标Fig. 10 Vertical stability index

4 结 语

基于UM多体动力学建模、田口试验以及稳健优化方法，分析了空气弹簧垂向刚度、垂向阻尼、横向刚度、横向阻尼以及油压减振器阻尼等5个悬挂参数对单轨车辆运行平稳性的影响关系。选择其中对平稳性影响较大的因素作为可控因子，利用田口实验法，研究了在不同车速、不同曲率半径及车辆载荷条件下车辆平稳性指标和其信噪比的变化规律。通过对田口试验结果进行信噪比分析，确定了对单轨车辆稳定性影响较大的悬挂参数的参数值，实现了悬挂系统的参数优化匹配。同时，对结果进行极差分析，确定了各噪声因子对于单轨车辆运行平稳性的影响从大到小依次为：运行速度、载荷水平、弯道半径。

对优化前后的单轨车辆进行仿真分析，结果表明：在不同组合的噪声水平及不同运行速度下，单轨车辆的横向平稳性指标和垂向平稳性指标均有不同程度的减小，单轨车辆的纵横向运行平稳性及抵抗外界干扰的能力有所提升，优化是有效的。