带动量项的梯度下降算法的收敛性
2021-12-30彭先伦
彭先伦, 谢 纲
(华东理工大学数学学院,上海 200237)
前馈神经网络目前已经得到了广泛的应用[1-2],而反向传播算法则被广泛运用于神经网络训练中,并且它的收敛性也在文献[3-4]中得到讨论。在反向传播算法中,经常会加入动量项来加速训练和使训练过程更稳定[5]。在有动量项的反向传播中,当前权重的更新量是损失函数对该权重参数的当前梯度与之前权重更新量的线性组合。
许多学者对有动量项的反向传播算法(BPM)进行过研究[6-8],文献[9]中给出了动量反向传播算法的稳定性分析,结果表明BPM 的稳定点就是平方误差损失的局部极小值,其他平衡点不稳定。Qian 在文献[10]中也讨论过BPM,表明系统在局部极小点附近的行为等价于一组阻尼谐波振荡器,动量项通过使系统的某些本征分量更接近临界阻尼来提高收敛速度。这些研究只是描述训练迭代过程在损失函数的局部极小值附近的行为,不能用于更一般的情况,比如随机选择初始权重。文献[11-12]中探讨了BPM 的收敛性,研究中限制损失函数的梯度是关于权重的线性函数,并且文献[12]中学习率和动量系数甚至被限制为常数,在这些限制下,BPM 的迭代过程稳定,其收敛性由迭代矩阵的特征值决定。但是,对于一般的激活函数比如Sigmoid 函数,损失函数对权重的梯度不是线性函数。文献[13]中针对没有隐藏层的简单网络证明了BPM 的全局收敛性。虽然这些结果对于任意给定的初始权重有效,但没限制损失函数的梯度是线性。文献[14]中证明了具有一个隐藏层的神经网络的BPM 的全局收敛性,以上研究中网络结构没有考虑偏置项且输出层只有一个输出神经元。
本文是对文献[14]中的结果的一个推广。本文所针对的神经网络具有一个隐藏层,但在网络结构中加入了偏置项,而且输出层可以具有任意个数的神经元,在不需要添加额外的假设的情况下,证明了BPM 的全局收敛性。
1 动量反向传播算法模型


有了输出后就可以得到通常的平方损失为:
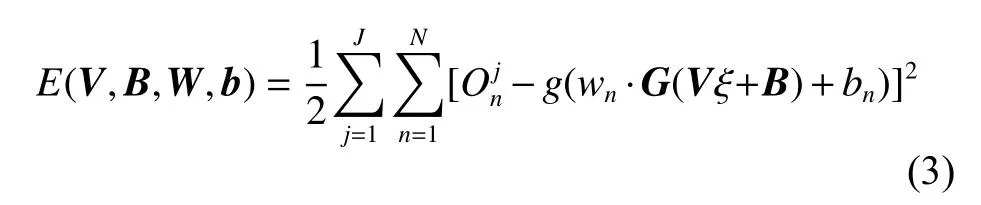
考虑到只需在每个输入 ξ 末尾都添加一项1,则输入层与隐藏层间的偏置向量可以合并到输入层与隐藏层之间的权重矩阵而不影响结果,这里设:
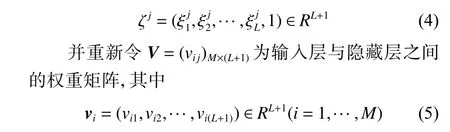
则输出层的输出可以重新表示为:
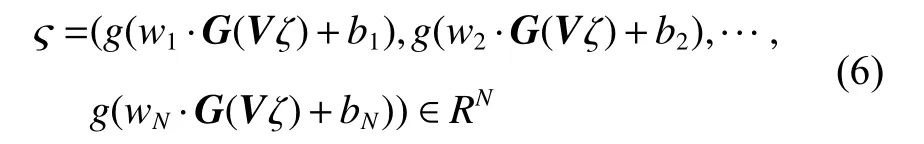
而网络的平方损失也可以重新表示为:
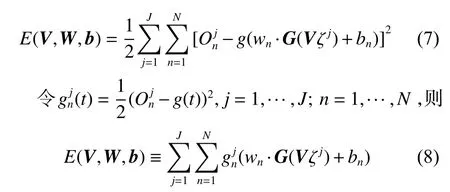
对网络进行训练的目的就是要找出最优的解(V∗,W∗,b∗) ,使得:
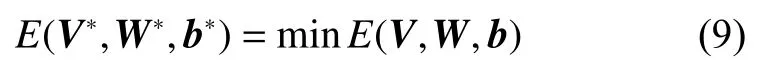
由式(7)可以得到损失函数关于V,W,b的导数分别为:

当任意给定了初始权重向量及偏置矩阵V0,V1,W0,W1,b0,b1时,BPM 通过下面的式子对权重向量及偏置矩阵进行更新:

类似于文献[12],动量系数 γk,i, τk,i及 κk,i分别设置为:
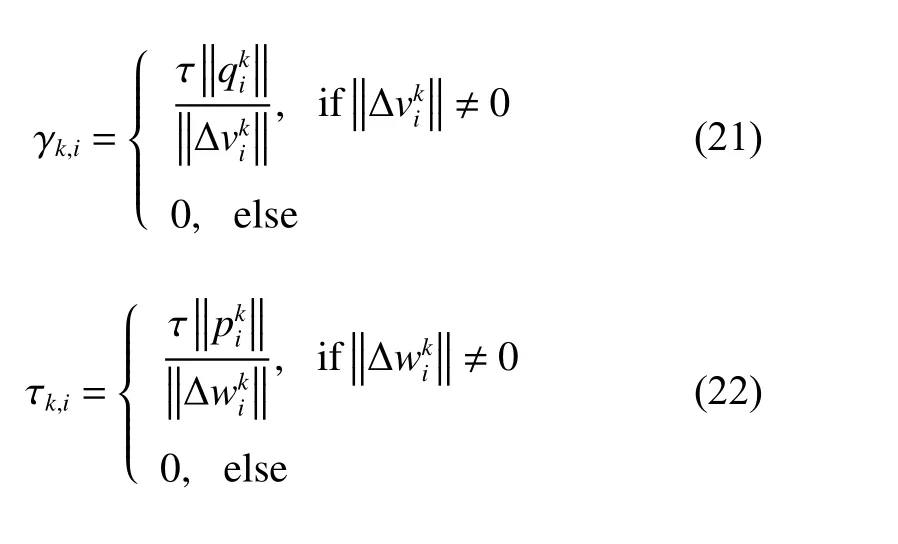

其中 τ ∈(0,1) 为动量因子, ‖·‖ 为欧几里得范数。
2 BPM 的收敛性相关假设及定理结论
在第1 部分中我们介绍了本文研究的动量反向传播算法模型,在该模型中参数是通过动量梯度下降算法不断地进行迭代更新,而对于整个迭代过程的收敛性需要进一步地研究,给出本文对于该模型的收敛性定理结论,在给出BPM 的收敛性相关结论之前,先提出几个需要用到的假设[13]:

最为常用的激活函数(Sigmoid 函数)是满足假设 ( 1) 的;假设 ( 2) 是为了保证式(25)~式(28)的弱收敛性,而在文献[15]中也作出了一个类似假设 ( 2) 来解决非线性问题;假设 ( 3) 要求损失函数只有有限个局部极小值点,这是为了保证式(29)~式(32)的强收敛性。有了假设 ( 1) 和假设 ( 2) ,我们很容易验证以下几条性质:

定理1 是主要结论。


3 关于模型收敛性定理1 的证明
接下来本文给出定理1 的详细证明过程,为了简化证明,引进下列符号:
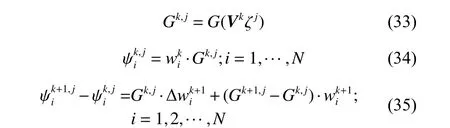
接下来本文提出几个有用的引理。
Step 3:Learning the past subjunctive mood based on Situation 2:Michael’s regrets.情景二中学习过去时的虚拟语气。教师通过ppt再现电影中主人公在得到一支神奇的人生遥控器之后生活发生了翻天覆地的变化,让主人公错过了生命中很多精彩而重要的时刻。教师尝试发问:(a)Why Michael’s life has changed so much?(b)Was Michael satisfied with his life here?Any regrets?
引理1:
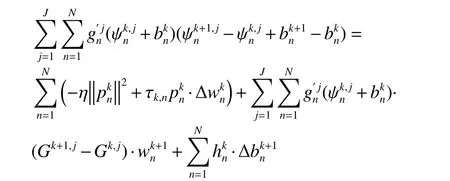
证明:由式(13)和(35)可知:
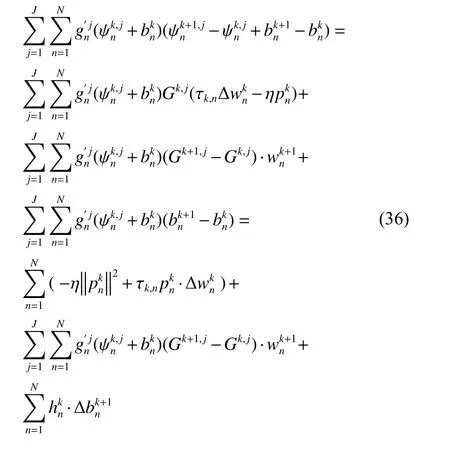
引理2:

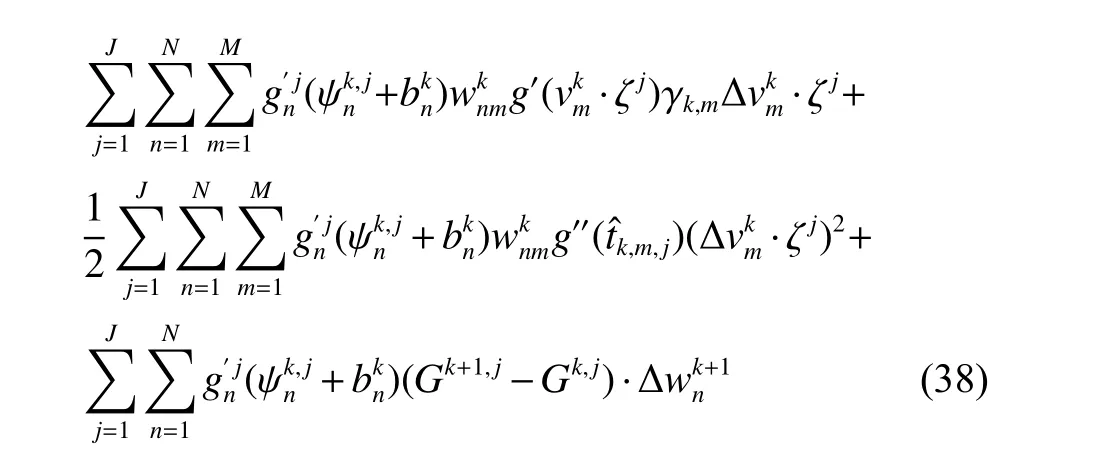
引理3:

证明:利用泰勒展开可得
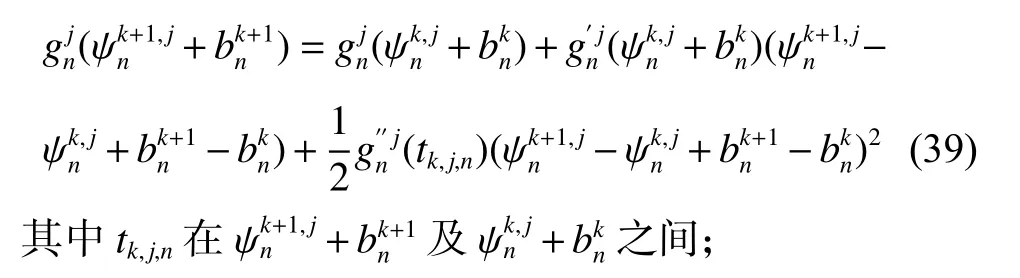
再结合引理1 及引理2 可知:
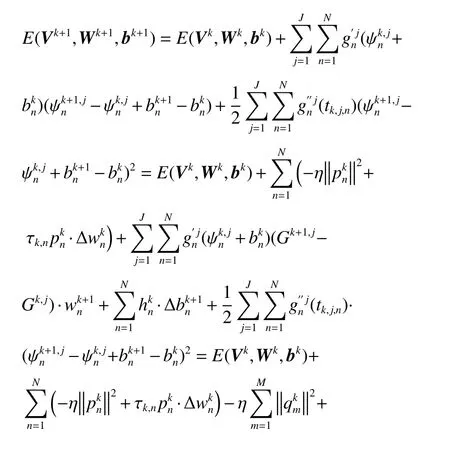


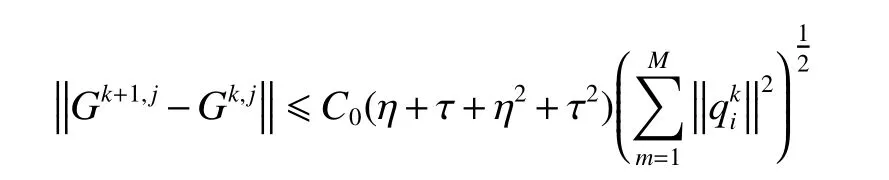
引理5:如果假设 ( 1) 和 ( 2) 成立,则存在常数C∗>0使得:



因此,由引理3 及引理5 可知:
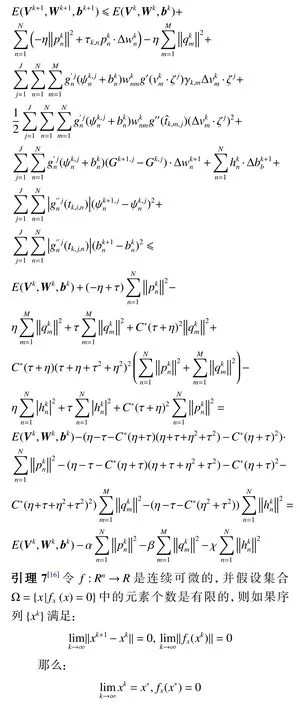
在有了这些引理之后,接下来就可以完成对定理1 的全部证明:
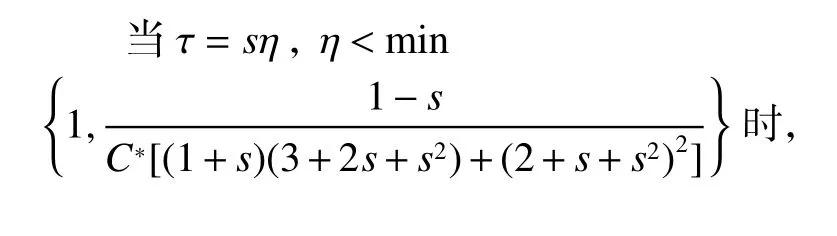

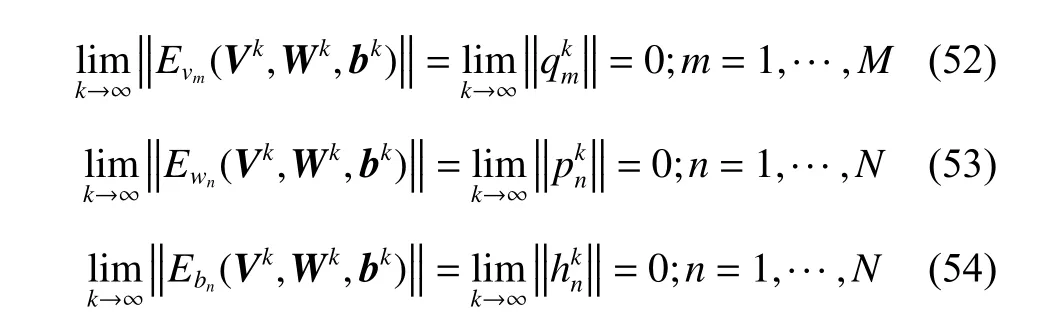
最后,由式(14~16)、(42)、(50)、(51)及式(52~54)可得:
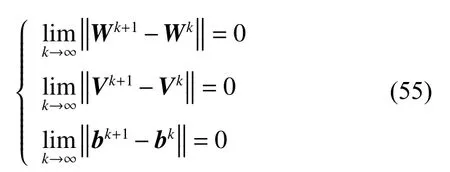
再结合引理7 以及式(55)即可得到式(29)~式(32);综上本文就完成了对定理1 的全部证明。
4 结 论
本文通过对动量反向传播算法模型进行理论分析,得出了相比目前已有的结果更具一般性的结论,即对于一个拥有偏置项的三层的神经网络,对其输出层神经元的个数不加限制,在几个简单而必要的假设下,该动量反向传播算法模型的训练迭代过程是可以收敛的,并且模型参数值也可以收敛到临界点。
