树上的最小-最大k 旅行商问题若干变种的精确算法
2021-12-30高哲成刘朝晖
高哲成, 余 炜, 刘朝晖
(华东理工大学数学学院,上海 200237)
树上的最小-最大k旅行商问题(Min-Maxk-TSPT)是多旅行商问题在树形结构中的推广问题。在Min-Maxk-TSPT 中,给定一个无向树形图T=(V,E) ,其中V是点集,E是边集,一个仓库s∈V,一个边权函数w:E→N ,以及k个旅行商,k是与输入无关的固定值。该问题的目标是找到一个k条环游的集合,其中每条环游都从s点出发并最终返回s点,并且使得T中每个节点都至少被一条环游覆盖,同时最小化其中最长环游的边权和。在更一般的Min-Maxk-TSPT 中,给定了一个候选仓库集D⊆V,每条环游需要从D中某个仓库出发并返回该仓库,若在Min-Maxk-TSPT中用子树来代替环游,就得到了树上的最小−最大k树覆盖问题(Min-Maxk-TCPT),类似地可以定义多仓库Min-Maxk-TCPT。由于树上的一条返回出发点的环游经过某个子树上的边为两次,所以多仓库Min-Maxk-TSPT 与多仓库Min-Maxk-TCPT 是等价的。
当k≥2 时,Min-Maxk-TSPT 是NP 困难的[1],因为Averbakh 等[2]证明了它可以归约到经典的平行机调度问题Pk||Cmax,因此本文着重于拟多项式可解性和近似性的结果。对于Min-Max 2-TSPT,Averbakh等[3]得到了4/3 近似算法,对于多仓库Min-Max 2-TSPT的一个变体,得到了一个3/2 近似算法,该变体的条件为 |D|=2 ,且两个旅行商必须从不同仓库出发。随后对于多仓库Min-Maxk-TSPT的给定D=V这一特殊情况,文献[2]给出了O(kk−1nk−1) 时间的(2−2/(k+1)) 近似算法。而Nagamochi等[4-5]也通过时间复杂度分别为O((k−1)!n) 和O(k2n) 的算法得到了相同的近似比。对于Min-M(axk-TSPT,N)agamochi等[5-6]还提出了时间复杂度为Onloglog1+ε/23 的 (2+ε)近似算法,其中 ε 为任意正常数。Becker 等[7]为Min-Maxk-TSPT 设计了多项式时间近似方案(PTAS),当仓库数量固定时,可以推广到多仓库Min-Maxk-TSPT。文献[5]和文献[7]中的结果实际上解决了k作为输入一部分的Min-Maxk-TSPT 及其多仓库问题。
与本文密切相关的结果是由Xu等[8]提出的对于Mi n-Maxk-TSPT的O(nW2k−2) 时间的拟多项式时间精确算法,其中W代表树中的总边权,研究者还将该算法推广到多仓库问题,因此对文献[2]和文献[3]中关于D=V时Min-Maxk-TSPT 是否在拟多项式时间内可解这一长达十五年未解决的问题给出了肯定的答案。
树形网络是一类重要的图,在实际应用如生产线中经常出现[9]。Min-Maxk-TSPT 及其多仓库推广问题以及一些变种问题在物流与服务行业有广泛的应用,包括维修、保养及货物运输等[2-3,8]。最小化最大返回时间这一目标则源于工作量安排的公平性需求以及限制最晚的返回时间[2-3]。
本文提出了针对Min-Maxk-TSPT 及其多仓库推广问题的新的拟多项式时间精确算法,其时间复杂度与Xu 等[8]的算法相同,但本文的算法精简了初始状态数量,将单个叶子点的初始状态数量从Xu 等[8]算法中的 2k种减少到了k种,因此在实际应用中将会有更好的表现。基于这种简化的算法,本文针对Min-Maxk-TSPT 的两个自然变体及对应的多仓库推广问题首次给出了拟多项式时间精确算法。其中一种变体被称为树上的最小-最大k路覆盖问题(Min-Maxk-PCPT),与Min-Maxk-TSPT 的区别在于此时旅行商无需返回出发点。另一种被称为树上的最小-最大k中国邮递员问题(Min-Maxk-CPPT),在该问题中,必须覆盖树的每条边而非每个节点。
1 问题描述及符号说明
给定一棵树T=V,E,其中V={1,2,···,n} 为顶点集(或点集),E为边集,s∈V是T的根节点,每条边e=(u,v)∈E有一个非负整数权重(长度),用w(e)或w(u,v) 来表示。P(u,v) 代表T中从u到v的唯一简单路,其长度用l(u,v) 来表示,P(s,v) 中边的数量定义为v的深度。P(s,v) 上除v外的所有节点称为v的前继节点,其中距离v最近的节点p(v) 则称为v的父节点。wv=l(p(v),v) 代表节点v与其父节点之间的边权,由于根节点无父节点,定义ws=0 。若u是v的一个前继(父)节点,那么v则被称为u的一个后继(子)节点。T(v)表示T中包含v及v的所有后继节点的子树。T的叶节点是在T中无子节点的节点,用Vleaf表示T中所有叶节点的集合,对于T的子树T′,T′的叶节点则指在T′中无子节点的节点。


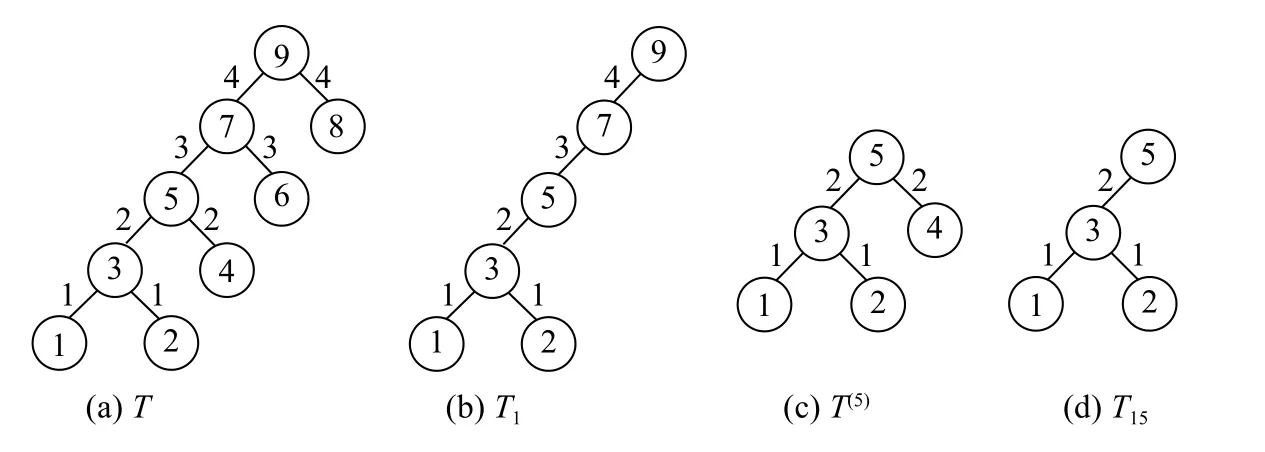
图1 T、Ti、Tij 以及T(i)的解释Fig. 1 Explanation of T、Ti、Tij and T(i)

2 预处理
对于一棵二叉树而言,当且仅当其中每个非叶节点恰好有两个子节点时,称其为完整二叉树(不同于满二叉树和完全二叉树)。若T是完整二叉树,则称 [T,w] 是一个标准实例。给定T=(V,E) 和w(·) ,可以通过下列步骤将实例 [T,w] 转换为一个标准实例[T′,w′] :
步骤1 令T′=T,w′=w。
步骤2 对于T′中只有一个子节点的点v,添加一个点v′和一条边 (v′,v) ,令w(v′,v)=0 。这样v′就成为v的第二个子节点。
步骤3 对于T′中拥有超过两个子节点的点v,设其子节点集为U,假定其中第一个子节点为u′。插入一个新节点v′作为所有u∈U{u′} 新的父节点并添加相应的边,令w′(v′,v)=0 ,w′(u,v′)=w(u,v) 。若v′仍有超过两个子节点,重复步骤3。
该转换方法在文献[8]中也有提及,此处重复表述是为了论述的完整性。图2 示出了一个转换的例子。一个 [T,w] 的可行解可以在多项式时间内转换为 [T′,w′] 的可行解,反之亦然。通过这样的转换,可以将处理每个点时的子节点固定为两个,从而简化后续算法的描述。
类似地,多仓库问题的实例 [T,w,D] 可以被转换为一个等价的标准实例 [T′,w′,D′]。D′包含D中所有点以及在步骤2 和步骤3 中产生的满足v∈D的新节点v′。如图2 所示,若原始实例中D={2,4,6} ,那么在经过转换后的实例中,D′={2,4,6,7,8,9} 。
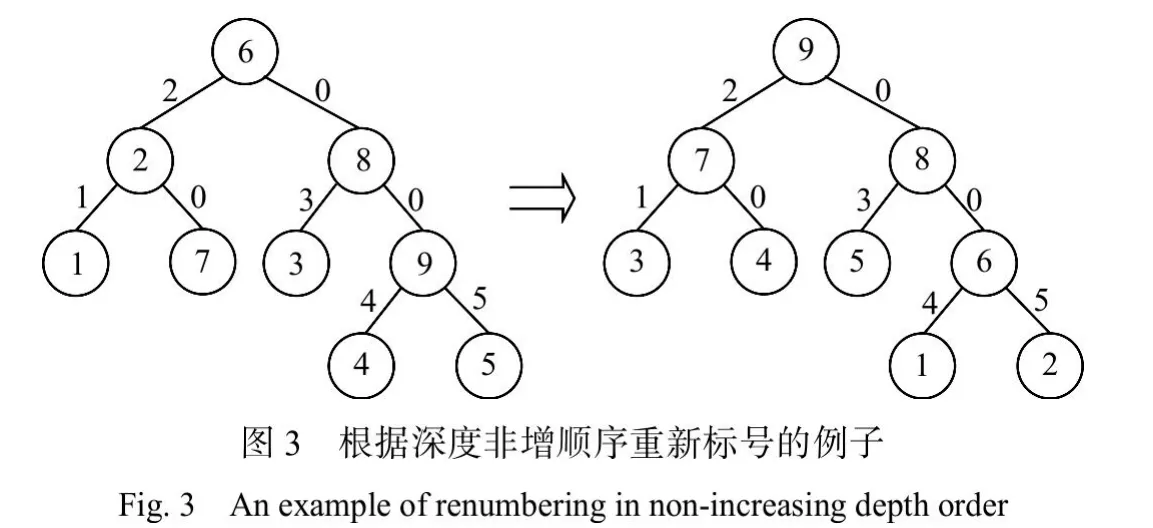
此外,对于一个标准实例,不失一般性,假设所有节点根据在T中的深度以非增顺序标号,这样的标号顺序保证了任意非叶子节点的序号都大于其子节点。图3 给出了一个根据图2 的转换结果重新标号的例子。
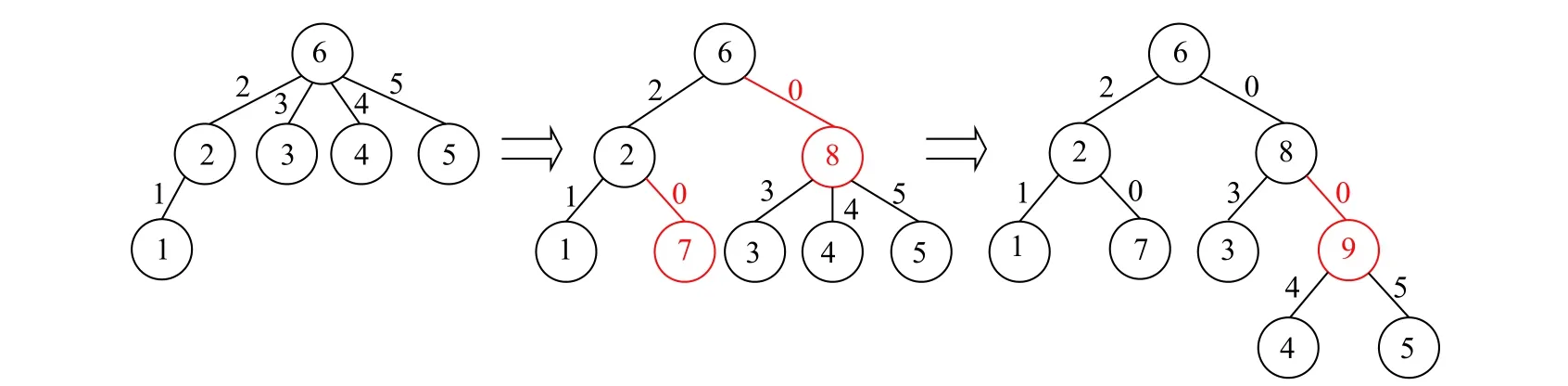
图2 标准实例的转换Fig. 2 Transformation of standard example
3 拟多项式时间精确算法
本节通过自下而上的动态规划方法对Min-Maxk-PCPT、多仓库Min-Maxk-TCPT、多仓库Min-Maxk-PCPT 以及多仓库Min-Maxk-CPPT 给出了拟多项式时间精确算法。
3.1 树上的最小−最大 k 路覆盖问题

输入:一棵子树T′,一个仓库s′。
输出:一条从s′出发的遍历V(T′) 的最短路P。



3.2 树上的多仓库最小-最大 k 树覆盖问题
本节针对多仓库Min-Maxk-TCPT 提出了下面算法2 这一拟多项式时间精确算法,它由算法1 推广而来,可以作为文献[8]中相应算法的替代并且相对简单,更重要的是它可以被调整以用于求解多仓库Min-Maxk-TCPT 的两个变种问题,在本文的3.3 节及3.4 节这两小节中将会呈现,算法2 如下:





表1 图1(c)作为实例时算法2 中的 H1 、 H2 和 H4 的结构Table 1 Construction of H1 , H2 and H4 by algorithm 2 for the instance in Fig. 1(c)

证明:引理3 的证明可通过对j=1,2,···,n进行归纳来完成。若j∈Vleaf,根据算法2 中的步骤1(b),必然存在一个初始状态满足引理3。而对于j∉Vleaf,j存在左右两个子节点l 表2 图1(c)作为实例时算法2 过程中的 H3 的结构Table 2 Construction of H3 by algorithm 2 for the instance in Fig. 1(c) 表3 图1(c)作为实例时算法2 过程中的 H5 的结构Table 3 Construction of H5 by algorithm 2 for the instance in Fig. 1(c) 本节通过将算法1和算法2 结合, 给出了多仓库Min-Maxk-PCPT 的首个拟多项式时间精确算法。 本文研究了Min-Maxk-TSPT 以及多仓库Min-Maxk-TSPT, 提出了新的经过改良的拟多项式时间精确算法, 并在此基础上对Min-Maxk-PCPT、多仓库Min-Maxk-PCPT 以及多仓库Min-Maxk-CPPT 首次提出了拟多项式时间精确算法。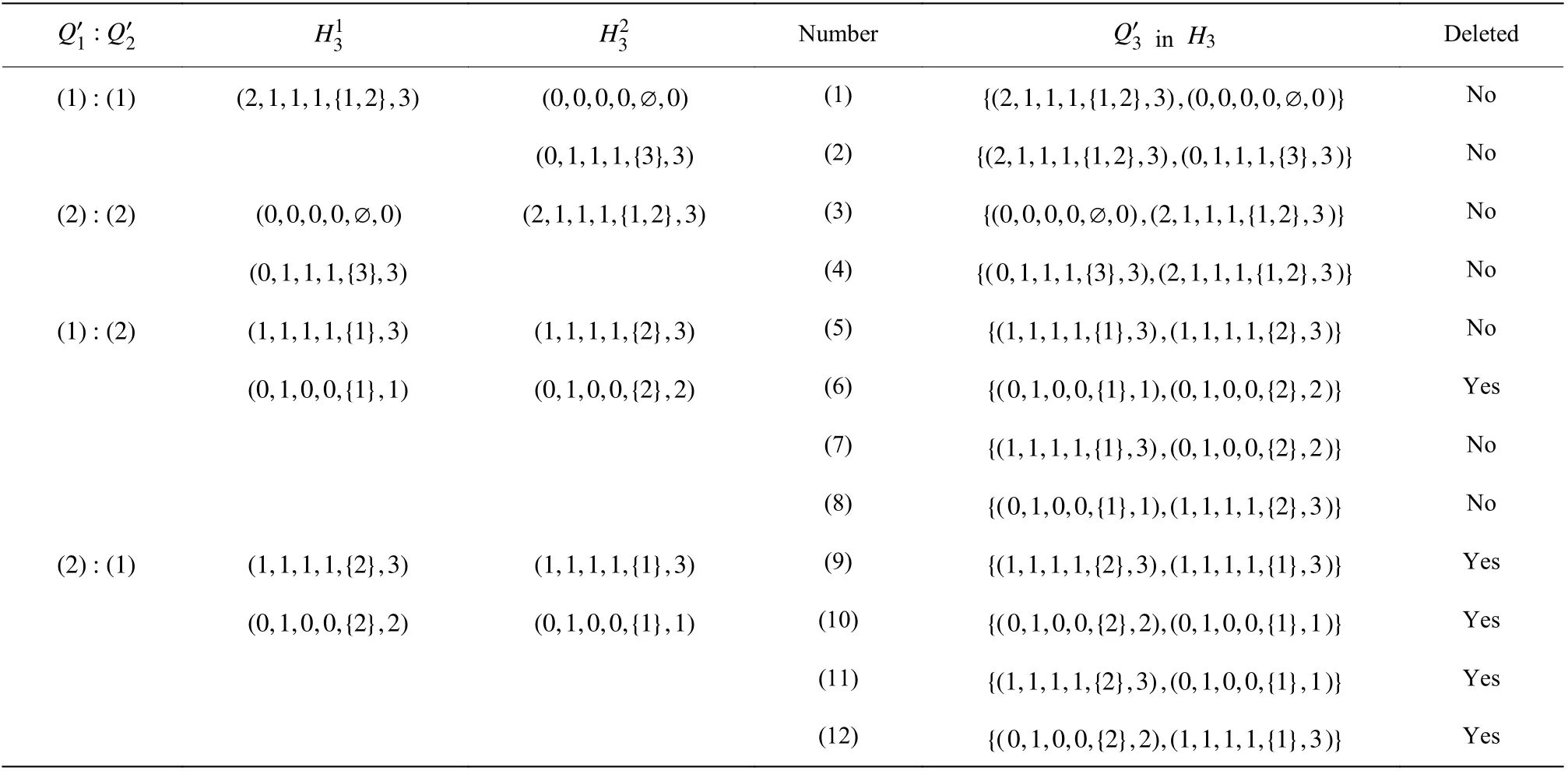
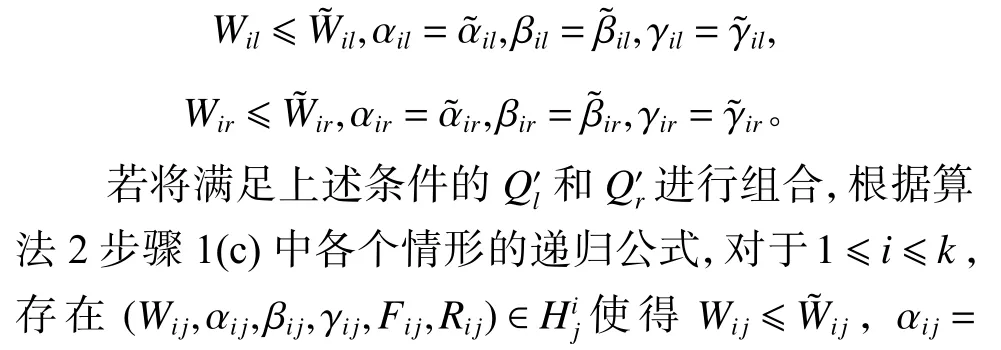



3.3 树上的多仓库最小-最大k 路覆盖问题


3.4 树上的多仓库最小-最大k 中国邮递员问题

4 结束语
