单晶硅微细铣削表面粗糙度预测模型及实验研究*

许顺杰,曹自洋,王浩杰

(苏州科技大学 a.机械工程学院；b.苏州市高效与精密加工技术重点实验室，江苏 苏州 215009)

0 引言

单晶硅是一种硬脆材料[1]，由于其有着出色的半导电性，从而被广泛地应用于微电子领域[2]。目前，增材制造无法普遍适用于晶体材料的加工，因此减材制造，如：光刻技术、化学蚀刻，被使用于MEMS半导体行业[3-5]，但是此类加工方式仅能加工平面2维或2.5维结构[6-7]。相比之下，微细铣削能够制造出特征尺寸几十微米到几百微米数量级的3维微结构，同时具有高精度、高表面光洁度，且机械加工方式安装简单[8]，相较于光刻机其设备成本低。

常温下，单晶硅属于脆性材料，加工时主要以崩碎的形式去除材料，只有在合适的切削参数条件下才能减少破损、降低表面粗糙度，从而提高加工表面质量[9-11]。Choong Z J等[6]通过对力、表面形貌和边缘质量进行试验测量，优化微铣削单晶硅的加工质量；Dehong H等[12]采用方差分析的方式，进一步分析了切削速度Vc、进给量f和轴向切削深度ap等切削参数的影响规律,从而确定了这些因素对铣削单晶硅表面粗糙度的影响；周云光等[13]利用微磨削技术手段，通过单晶硅表面粗糙度的数值分析，优化了磨削工艺参数；Liu B等[14]研究了单晶硅在脆性、延性模式下的材料去除过程，研究表明在延性模式下的切削表面有更少的裂纹和破损，表面质量更好。虽然国内外学者对单晶硅表面质量进行了很多方面的研究，但是由于单晶硅是一种硬脆材料，针对其表面粗糙度的预测模型不易建立和验证。

本文将基于回归分析构建单晶硅微细铣削表面粗糙度的预测模型，采用正交实验的方法来研究微细铣削参数对单晶硅表面粗糙度的影响规律，并进一步分析单晶硅加工后的表面完整性，从而根据工况选择最优化的工艺参数，达到提高表面质量的目的。

1 基于表面粗糙度预测模型的线性变换

根据文献[15]可知，每齿进给量fz、主轴转速n、轴向切深ap可以根据实验参数来建立相应的数学模型，以此来构建非线性幂函数的微细铣削表面粗糙度模型为：

Ra=cnkfzlapm

(1)

式中，c是根据加工材料和试验参数确定的系数；k、l、m是微铣削三因素所占影响比例的大小。

对式(1)等式两边进行对数运算转化为线性函数，即：

lgRa=lgc+klgn+llgfz+mlgap

(2)

令b0=lgc,b1=k,b2=l,b3=m,x1=lgn,x2=lgfz,x3=lgap,y=lgRa，代入式(2)则可变为：

y=b0+b1x1+b2x2+b3x3

(3)

为了计算式(3)中b0、b1、b2、b3的数值，减少试验次数，采用正交表L16(43)设计实验，共计16组。第i组的实验的自变量用xi1、xi2、xi3来表示，因变量用yi来表示，εi表示对应组的误差，则构建的数学模型为：

(4)

式(4)可改写成：

(5)

设b0、b1、b2、b3依次是β0、β1、β2、β3的最小二乘估计，即数学模型的回归系数，则根据式(3)可以表示回归方程：

(6)

2 单晶硅微铣削实验

2.1 实验材料及设备

实验工件材料为单晶硅，因(100)晶面原子密度小、原子间距离大、晶面结合力相对较弱、便于加工，且摩擦系数稳定，加工后可得到较完整的表面，故选取(100)单晶硅片进行全槽铣削。机床加工原理示意图如图1所示，将直径4英寸硅片切割成条状，利用AB胶黏贴在修整后的黄铜表面，用WIFI便携式数码显微镜确保对刀精度。本实验设备采用哈斯三轴联动数控加工中心，微铣刀采用台湾某公司生产的刃径0.5 mm的金刚石涂层2刃平头立铣刀，刃长1 mm，刀尖圆弧半径约为13.8 μm，采用VHX-5000超景深三维显微镜观测加工表面形貌，通过Contour GT-K0白光干涉仪对加工后的单晶硅槽底进行粗糙度测量。

图1 加工原理示意图

2.2 实验方案

单晶硅属于硬脆材料，在高速切削下会产生大量的热[6]，故选择水基切削液对其进行冷却。选择每齿进给量fz、主轴转速n、轴向切削深度ap三个切削要素，加工单晶硅易产生裂纹和破损，最大未变形切削厚度dmax是评价微细铣削加工的一个重要指标[16]，如下式：

(7)

式中，R是铣刀刀尖圆弧半径；fz是每齿进给量；ap是轴向切深。

通过计算最大未变形切削厚度dmax[17]能初步判断单晶硅的加工状态,根据文献[18]可知，单晶硅的临界切削厚度hc≈110 nm,为使dmax小于hc，需要选取较小的每齿进给量，考虑机床转速和切削散热选取主轴转速10 000～30 000 r/min，根据微铣刀的有效刃长和加工条件选择切削深度为5～15 μm，按照L16(43)设计单晶硅微铣削实验，如表1所示。为了节约材料和便于观测表面质量，选择铣削微槽来观测表面质量，其尺寸如图2所示，槽长度A=5 mm，每个微槽间距B=3 mm，宽度C=0.5 mm。

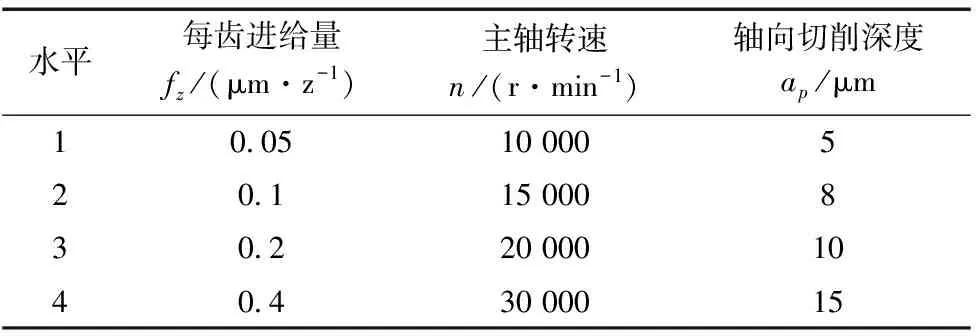
表1 因素水平表

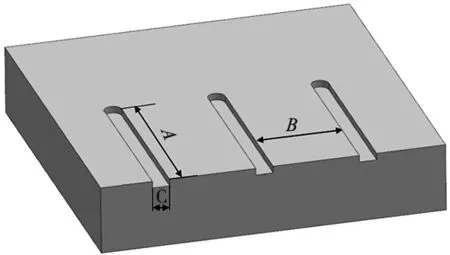
图2 微槽尺寸示意图

3 实验结果与分析

3.1 表面粗糙度测量结果

在铣削单晶硅微槽实验后，采用Contour GT-K0白光干涉仪对实验加工后的表面进行粗糙度测量，选择微槽中线的前中后三段取样，取其平均值为微槽底面粗糙度数值，数据详见表2。

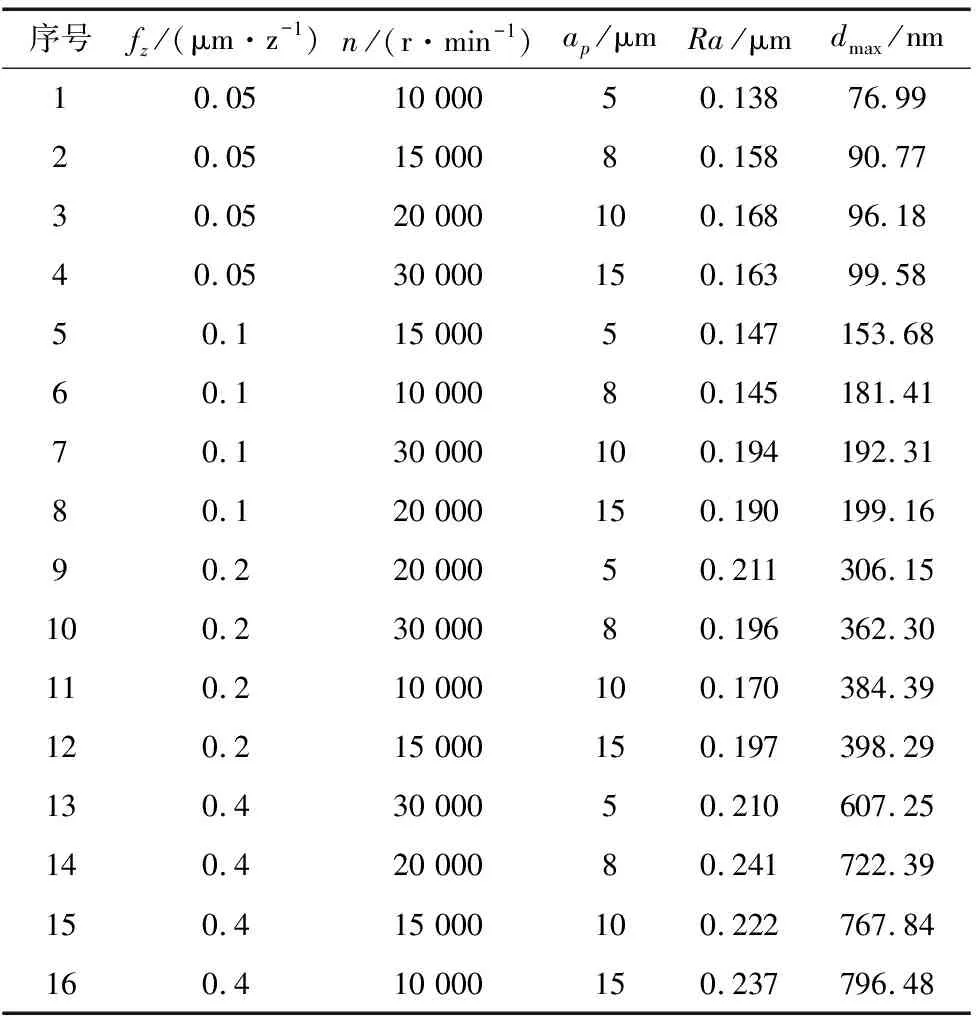
表2 正交实验结果

3.2 表面粗糙度分析

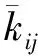
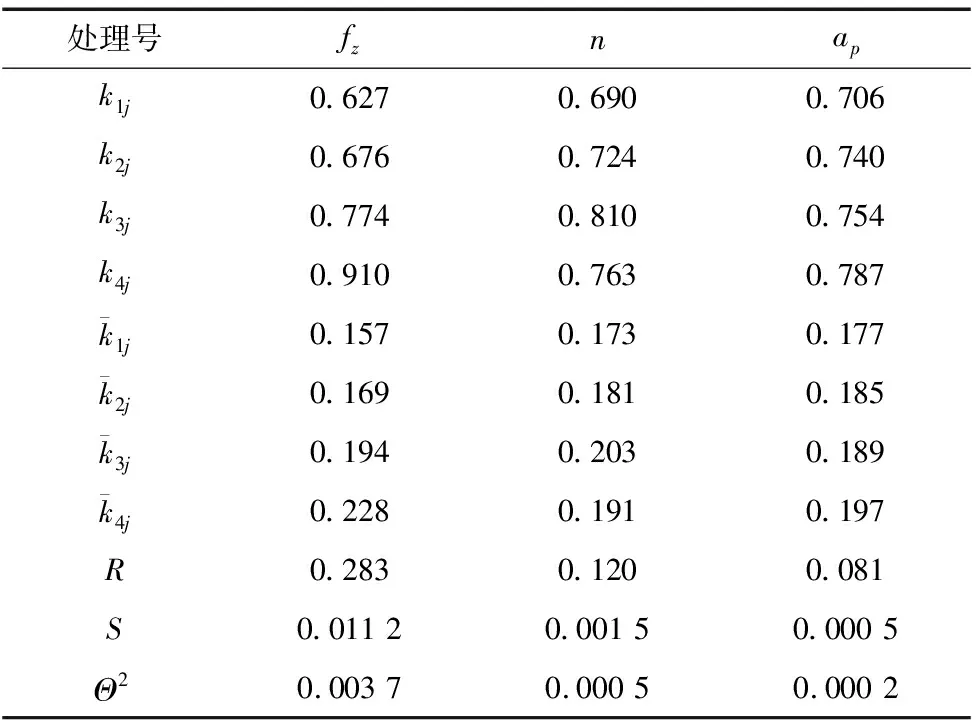
表3 表面粗糙度分析结果

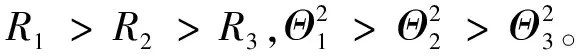
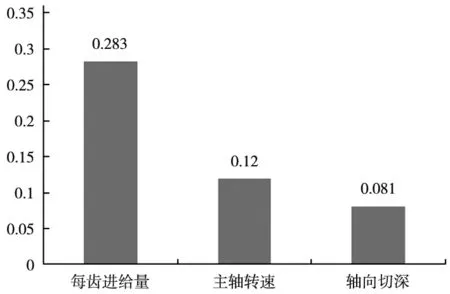
(a) 极差图

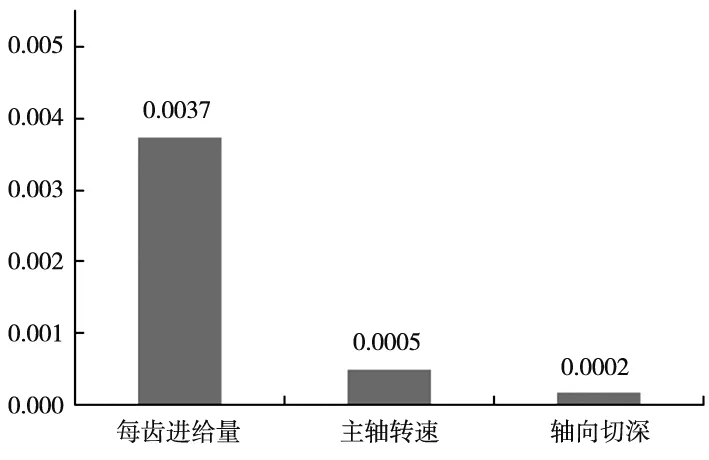
(b) 方差图图3 极差图和方差图

分别对三个切削要素进行分析。

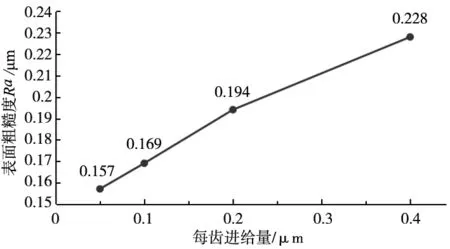
图4 每齿进给量对Ra的影响

由图4可知，随着每齿进给量fz的增加，表面粗糙度Ra呈现上升趋势，这是因为随着每齿进给量的增加，铣削效率提高，铣削力上升，加快了单晶硅表面的裂纹破损和微铣刀的磨损，使得其表面粗糙度上升，表面质量降低。

从图5中可以看出，主轴转速从10 000 r/min增至20 000 r/min，表面粗糙度呈现上升趋势，从20 000 r/min增加到30 000 r/min，表面粗糙度逐渐下降。这是由于随着主轴转速n的提高，工作区温度升高，导致铣刀与硅屑发生粘结现象，生成积屑瘤，从而加剧了单晶硅的破碎，当转速达到一定后，切削进入稳定去除阶段，表面粗糙度得到降低。另外随着主轴转速的提高，切削力降低，使得其表面粗糙度下降[19]，从而提高表面质量。

图5 主轴转速对Ra的影响

根据图6可知，轴向切深ap从5 μm到15 μm逐渐增加，粗糙度值也从0.177 μm增至0.197 μm，但变化趋势不显著，说明轴向切深ap对表面粗糙度的影响不大。

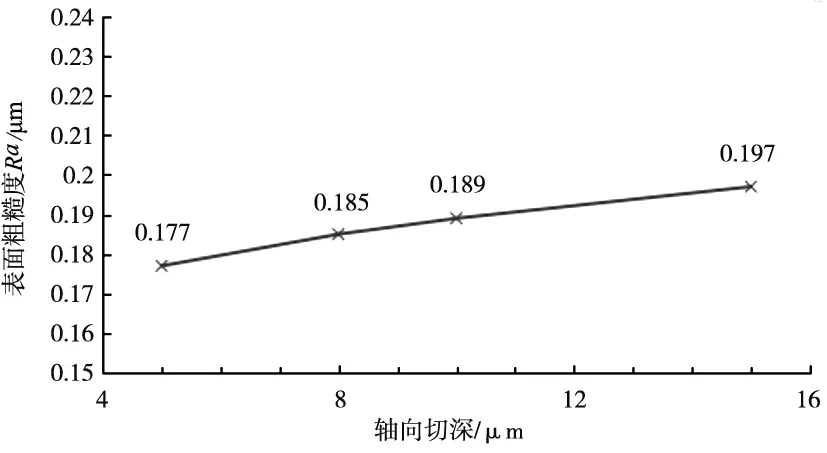
图6 轴向切深对Ra的影响

3.3 表面完整性分析

不同每齿进给量加工后的表面形貌，如图7所示。

(a) fz=0.05 μm (b) fz=0.2 μm图7 不同每齿进给量加工的表面

从图7中可以看出，当每齿进给量从fz=0.05 μm增加到fz=0.2 μm时，单晶硅表面的刀齿纹路间距增大，表面破损加剧，导致表面粗糙度Ra变大。从图中也可以看出随着每齿进给量从fz=0.05 μm扩大到fz=0.2 μm后，表面的凹坑数量变多，破损加剧，这进一步导致表面粗糙度增大，表面质量下降。

由图8可以看出，微槽存在阶梯状的边缘，这是由于加工中刀具存在磨损，刀具两刃磨损不一致，存在单刃切削，磨损少的一刃在铣削时会优先接触边缘进行铣削。从图8a可以看出边缘存在破损，这是加工过程中的裂纹扩展和位错运动的共同作用[20-21]而产生的。

(a) 二维形貌图 (b) 三维形貌图

切削方式示意图如图9所示，由图9a可知刀具旋转方向(顺时针)和工件进给方向V。刀具在铣削微槽一侧时(A侧)，铣刀的旋转方向和V相反，即铣削微槽A侧时是逆铣加工模式；刀具在铣削微槽另一侧时(B侧)，铣刀的旋转方向和V相同，即铣削微槽B侧时是顺铣加工模式。见图9b，逆铣模式下的微槽一侧表面光滑，无凹坑、破损，而处于顺铣模式下的一侧表面存在凹坑、破损，且边缘质量较差，由此可知，逆铣模式下的微槽一侧表面质量明显优于顺铣模式下的微槽另一侧，所以为了减少破损，提高表面质量，可以使用侧铣的工艺方式来实现。

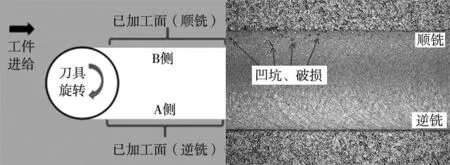
(a) 微铣削示意图 (b) 单晶硅微槽图9 单晶硅微铣削切削方式示意图

4 表面粗糙度预测模型的构建和评价

根据单晶硅表面粗糙度预测模型的回归方程式(6)，对16组实验的参数数值取e为底的对数，并使用MATLAB对数据进行回归分析，由式(7)可计算出b=[-2.825 1 0.128 1 0.182 2 0.109 5]T，即回归方程为：

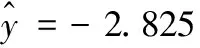
(8)

因此，粗糙度预测模型可表示为：

Ra=e-2.825 1n0.128 1fz0.182 2ap0.109 5

(9)

对得到的预测模型进行显著性检测，从而判断预测模型的优劣程度。拟合效果用总的离差平方和ST，回归平方和SR，残差平方和SE来衡量，如式(11)～ 式(13)所示：

(10)

(11)

(12)

利用F检验，为了要检验y和xi1、xi2、xi3的线性关系，则令β1=0，β2=0，β3=0,那么:

(13)

式中，F是两方差之比，它服从自由度为m，n-m-1的F分布；n是实验次数，n=16；m是变量个数，m=3。

由式(11)～式(14)，求出相关数值，详见表4。

表4 预测模型显著性分析表

当ɑ=0.05时，根据F分布表知F(3,12)=3.49，而F比为21.89远大于F(3,12)值，所以微铣削单晶硅表面粗糙度的预测模型是高度显著的。

回归方程的相关系数R2越接近1，回归效果就愈好，自变量X与因变量Y的相互关联程度就越高。

(14)

根据式(14)计算可得R2=0.85，进一步表明构建的预测模型是可靠且显著的。

图10是5%的置信区间图，样本点的残差值都在置信区间上下限内，未出现异常数据点，可见预测模型是正确且可靠的。

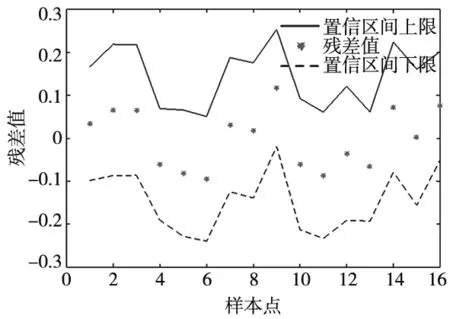
图10 置信区间和残差图

5 预测模型的可靠性验证

由极差和方差分析可以得到，在实验参数范围内，获得的最优工艺参数为每齿进给量0.05 μm，主轴转速10 000 r/min，轴向切深5 μm，本组工艺参数在正交实验内，故考虑因素次优组合等情况，另外设计3组加工参数来进行对比，验证此模型的可靠性，如表5所示。

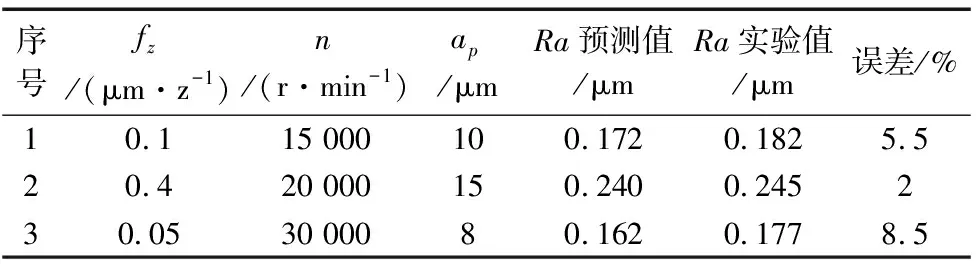
表5 预测模型验证数据

由表5可知，3组实验的表面粗糙度实验值均大于最优工艺参数对应的粗糙度值，且3组实验和预测粗糙度值的误差在2%～8.5%之间。由此可见，构建的单晶硅微细铣削表面粗糙度预测模型具有较高的可靠性和精度。

6 结论

本文针对单晶硅微细铣削，提出了单晶硅表面粗糙度的预测模型，根据正交实验得到切削要素和表面粗糙度之间的关系，分析了切削要素和切削方式对表面形貌的影响，验证了预测模型的可靠性，得出以下结论：

(1)微细铣削单晶硅表面粗糙度影响程度依次为：每齿进给量、主轴转速、轴向切深。参数的选择需根据实际情况确定，在实验参数范围内，获得的最优工艺参数为fz=0.05 μm，n=10 000 r/min，ap=5 μm。

(2)刀具磨损会影响微槽铣削质量，存在单刃切削的情况。逆铣模式下的微槽一侧表面质量优于顺铣模式下的微槽一侧。

(3)基于多元线性回归构建了单晶硅微细铣削表面粗糙度的预测模型，通过F检验，相关系数R2和置信区间的计算分析，验证了预测模型的可靠性。

(4)通过可靠性验证实验，验证了实验得到的最优工艺参数的最优性，预测值误差均在合理范围内，也证明了此模型的可靠性和准确度。