基于逻辑回归的测量图像亚像素边缘定位*

段振云，庞文琦，张 静，赵文珍，赵文辉，杜 坡

(沈阳工业大学机械学院，沈阳 110870)

0 引言

采用机器视觉测量技术对零件尺寸进行检测具有高效、非接触等优点[1-5]。视觉测量是通过处理零件图像的边缘来获得零件的尺寸，所以对零件图像进行边缘定位是视觉测量中基础且关键的内容，是后续测量的前提。

测量系统采集图像时，通常采用平行背光源照明，图像前景和背景对比度较高，测量图像中工件轮廓清晰，易得到高精度的工件边缘。为还原工件真实尺寸，宜选用高分辨率相机，但是相机的分辨率越高，价格越昂贵，且分辨率达到一定程度时，对提高边缘定位精度的效果不大。传统的像素级边缘定位算法无法满足高精度测量要求[6]。因此，对于测量图像则需要高精度的亚像素边缘定位算法。目前的亚像素边缘定位算法主要分为三大类[7-9]:矩法、插值法和拟合法。魏本征等[10]提出的矩法计算量小，抗噪性好，解决了Z矩运算复杂的问题，但该算法对细小边缘的定位效果不好。孙秋成等[11]提出的插值算法对噪声的鲁棒性好，解决了模糊边缘模型拟合过程中需要对非线性的目标进行优化求解而导致算法速度慢的问题。但该法不适用于曲线边缘。段振云等[12]提出的高斯积分曲面拟合法不需要进行梯度幅值计算，解决了传统高斯拟合法中梯度幅值会对边缘定位产生影响的问题，但该算法计算复杂，速度较慢。

针对以上问题，本文提出一种基于逻辑回归的边缘定位算法。利用逻辑回归的统计思想，找到前景与背景的分类边界即为亚像素边缘，算法适用于任意形状边缘且简化了标定过程。本文给出了标准量块基于亚像素边缘定位的误差测量结果，并与拟合法[12]和Z矩法[13]进行了比较实验，验证本文算法具有较高的边缘定位精度。

1 逻辑回归边缘定位算法

1.1 逻辑回归原理

逻辑回归[14]又称Logistic回归，是人工智能、机器学习中的经典分类方法，常用来解决二分类问题[15]。逻辑回归计算结果为分类概率，默认阈值为0.5，概率大于0.5视为正类，输出结果为1；概率小于0.5视为负类，输出结果为0，正类与负类的分类边界为决策边界。逻辑回归的思想是先根据边界类型构建一个边界模型和一个预测函数，再建立一个预测函数的损失函数，最后通过优化方法找到边界的最佳回归系数。

逻辑回归的边界模型一般可以表达为：

(1)

式中，X=[x1,x2,x3,…,xn]为自变量矩阵，θT=[θ0,θ1,θ2,…,θn]为回归系数。

逻辑回归的预测函数为Sigmoid函数，所以概率预测函数为：

(2)

设yi为观测值，则yi=1的概率为hθ(Xi)，即：

P(yi=1|Xi)=hθ(Xi)

(3)

则yi=0的概率为：

P(yi=0|Xi)=1-hθ(Xi)

(4)

所以观测值为yi概率为：

P(yi|Xi)=(hθ(Xi))yi(1-hθ(Xi))1-yi

(5)

采用最大似然估计法对逻辑回归的回归系数进行估计，m个yi的似然函数为所有样本的预测概率之积：

(6)

取对数似然函数的平均值，令平均值的负值最小即为逻辑回归的损失函数:

(7)

式中，Xi，yi分别表示第i个样本的自变量矩阵和对应的实际概率，当hθ(Xi)=0.5时，损失函数最小时，此时求得最佳回归系数θT。

1.2 测量图像边缘特征

图像理想的边缘特征是阶跃函数，如图1a所示,但在实际情况中，存在光能的扩散效应，因此实际边缘模型符合高斯分布函数，如图1b所示。

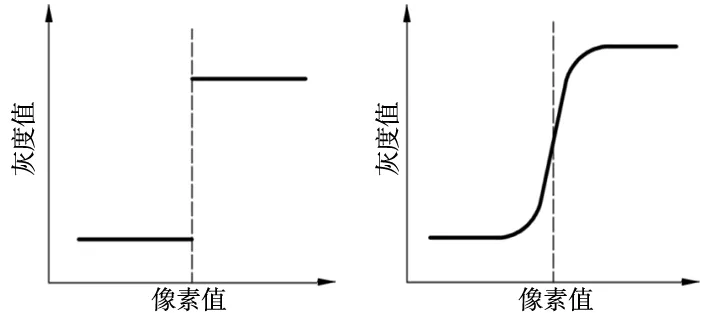
(a) 理想阶跃边缘 (b) 实际阶跃边缘图1 阶跃边缘的灰度分布

Sigmoid函数是一个连续、光滑、且严格单调的阈值函数，其表达式为：

(8)

对应的函数图像如图2所示。

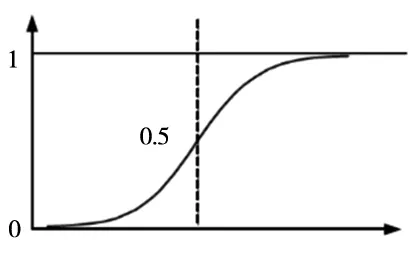
图2 Sigmoid函数

可以看出，Sigmoid函数与实际边缘灰度分布曲线十分贴近，因此可以用Sigmoid函数来拟合图像边缘[16]。

将图像的灰度值归一化处理，则前景灰度值为0，背景灰度值为1。像素点的灰度值可以视为该点为背景的概率。以Sigmoid函数为预测函数的逻辑回归算法，能够有效地解决二分类问题，并且逻辑回归的预测函数与图像的实际边缘灰度曲线十分贴近，因此可以利用逻辑回归对前景和背景进行分类，找到图像边缘。

1.3 逻辑回归图像边缘定位模型

边界模型从原理上讲可以是任意曲线模型，但根据工程实际情况且为了简化计算，本文使用两种边界模型，分别为直线和圆弧。本文算法分为两种方法，一种是当边缘形状已知为直线或圆弧时，直接构建直线模型或圆模型代入逻辑回归算法，可以一次性回归得到边缘位置；另一种是当边缘形状未知时，在很小范围内可以将边缘可以看作直线，利用逻辑回归算法分段统计出各个范围内的边缘位置，即可得到完整边缘。

直线边缘模型为：

z=θTX=θ0+θ1x1+θ2x2

(9)

式中，X=[1,x1,x2]。

圆弧边界模型为：

z=θTX=θ0+θ1x1+θ2x2+θ3(x12+x22)

(10)

式中，X=[1,x1,x2,x12+x22]。

在式(9)和式(10)中，x1和x2分别为像素点的横坐标和纵坐标。计算边缘时，将边界模型代入预测函数，预测函数的损失函数最小时，θT为最佳回归系数，将最佳回归系数代回边界模型，可计算出亚像素边缘点坐标(x1，x2)。

1.4 边缘定位算法的实现

采用本文算法定位边缘时，先设置高低阈值分别确定出连续的粗边缘带，如图3所示。当边缘形状已知为直线或圆时，如图4所示，对粗边缘带上的点进行拟合得到粗边缘，在粗边缘的两侧分别取距离为p个像素的等距线，得到宽度为2p个像素的逻辑回归区域，逻辑回归区域的宽度大于边缘过渡带的宽度，对逻辑回归区域上的点一次性进行逻辑回归，统计出亚像素级边缘。当边缘形状未知时，可进行分段逻辑回归，如图5a所示，取粗边缘带上的点为中心点，在中心附近确定一个大小为q×q方阵的逻辑回归区域，使逻辑回归区域能够包含边缘过渡带，对逻辑回归区域内的点进行逻辑回归，得到最佳回归系数，计算出一条直线，令中心点为原点，比较x轴截距Δx和y轴截距Δy二者的绝对值大小，取离原点近的截距点为亚像素边缘点，如图5b所示，在粗边缘带上每隔k个点取一个中心点，重复算法直至边缘定位结束，即可得到亚像素边缘。

图3 提取边缘

图4 一次逻辑回归定位边缘局部放大图

(a) 边缘定位局部放大图

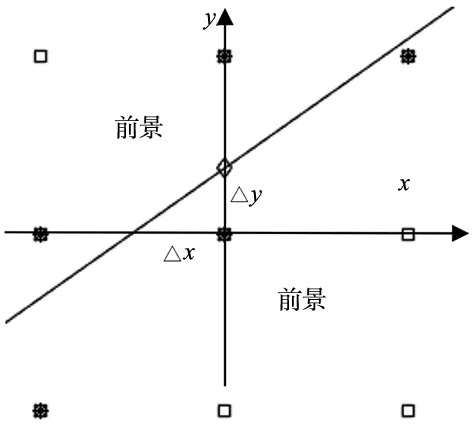
(b) 分段回归局部示意图图5 分段逻辑回归定位边缘

2 光源强度标定与边缘位置补偿

在视觉测量时，图像中零件的边缘会随着光源强度变化而沿其法向偏移，光强提高，零件的真实边缘点的灰度值小于0.5；反之，零件的真实边缘点的灰度值大于0.5。因此，使用视觉测量系统测量零件尺寸前必须对测量系统进行光源强度标定，对获取的边缘进行边缘偏移量补偿。

本文根据逻辑回归边缘定位算法的特点，提出了一种光强补偿系数，调节系数可以改变边前景与背景的分类位置，即将前景与背景的边界由0.5设定为(0.5+δ)。具体算法为：设置一个初始光前补偿系数δ代入量块边缘定位中，根据量块的测量尺寸与实际尺寸之差自动调整系数δ，当尺寸之差小于一定的范围时，δ为最佳光强补偿系数。在一定的光强条件下标定δ后，将δ代入后续的零件测量中，即可得到精确的测量边缘位置。

3 实验分析

为了验证本文提出的基于逻辑回归边缘定位算法的有效性，分别采用本文算法、高斯积分曲面拟合法和改进的Zernike正交矩算法进行边缘定位实验，根据定位的零件边缘可以计算出零件的图像尺寸，零件的图像尺寸乘以像素当量可以得到零件的实际尺寸。本文实验条件下的像素当量等于19.472 1 μm。其中本文算法分为分段逻辑回归方法和一次逻辑回归两种方法。

实验选用2个不同尺寸的0级标准量块进行几何量误差测量。量块的测量面精度可以达到0.05 μm，并且边缘简单，可以用于验证算法的精度。图6为量块的4种位姿图像。

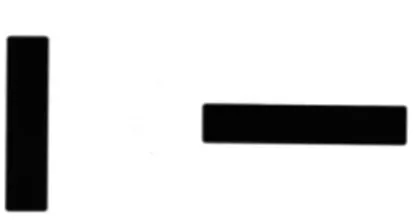
(a) 位姿1 (b) 位姿2

(c) 位姿3 (d) 位姿4

分别采用三种算法进行边缘定位，结果如图7所示。可以看出三种算法定位的边缘具有一致性，可以证明本文算法的有效性。

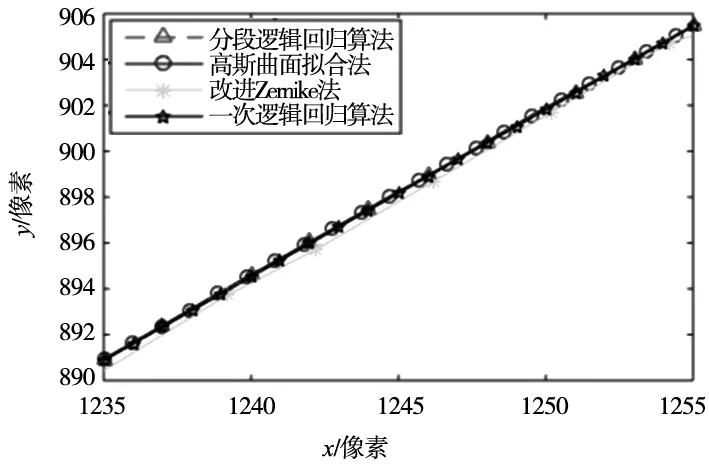
图7 亚像素边缘

利用三种算法分别测出量块亚像素边缘，得到算法测量误差曲线，从图8所示的边缘点的跳跃程度可以看出，本文算法获得的亚像素边缘平滑，边局部跳跃量较小。分别计算三种算法所确定的亚像素边缘的平均算法误差并进行比较，结果如表1所示。

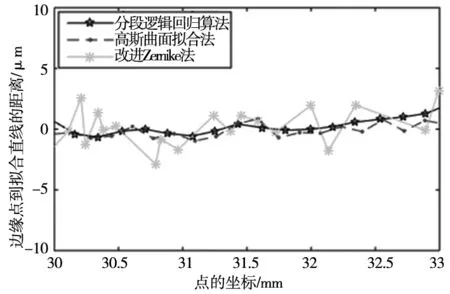
图8 测量误差曲线

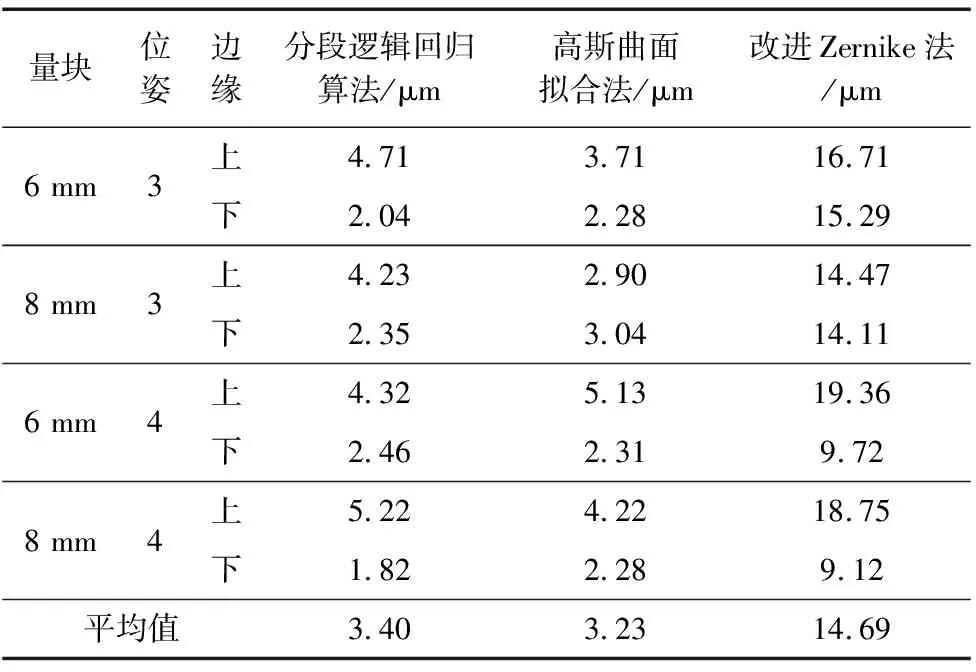
表1 测量误差

从表1、图8中可以看出，本文算法可以将测量误差控制在很小的范围内，边缘定位精度较高。

使用三种算法对量块直线边缘进行定位，对同一量块的不同位姿进行边缘定位，计算两条边缘的距离记为测量尺寸 ，测量尺寸与理论尺寸的差值即为量块尺寸测量误差。测量结果如表2所示。

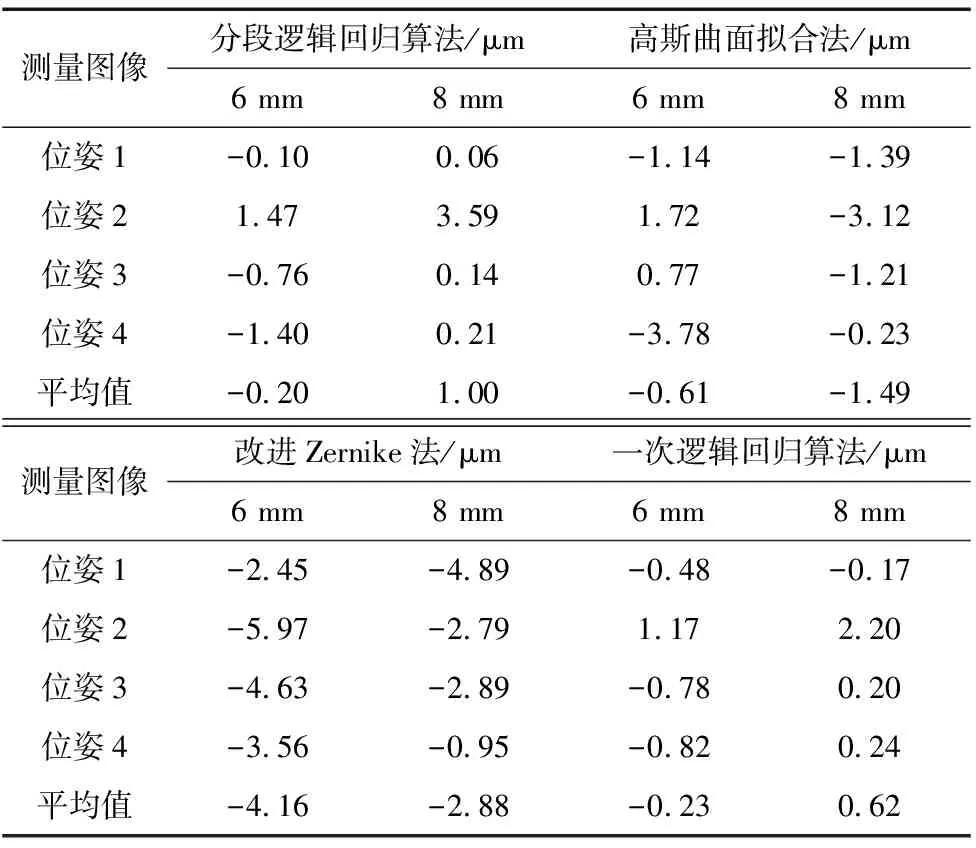
表2 尺寸测量误差比较

4 结论

本文提出一种基于逻辑回归的边缘定位算法，将逻辑回归算法应用于高精度零件图像边缘定位，利用统计的思想，将前景与背景进行分类，找到分类边界即为亚像素边缘。与基于高斯积分曲面拟合亚像素边缘定位算法相比，本文算法更为简单，减少了计算量，提高了计算速度；与基于Zernike正交矩的图像亚像素边缘检测算法相比，本文中设有光强补偿系数，简化了光强标定方法，可以有效补偿光源强度造成的边缘定位误差。通过实验可以看出，本文算法整体精度较高，能够稳定可靠地定位图像边缘，检测零件的精度，在高精度零测量上具有良好的应用前景。