基于地表电位幅值和相角的接地网故障诊断方法研究

权学政，李朝霞

(西藏农牧学院 电气工程学院，西藏 林芝 860000)

0 引 言

变电站之所以能安全稳定运行，接地网起到了关键的作用。而当接地网出现腐蚀变细或腐蚀断裂时，就会发生事故，从而影响电力系统的稳定运行，造成设备损坏，带来经济损失[1]。因此准确诊断并定位接地网的故障位置对电力系统的安全运行有着非常重要的意义。

传统接地网故障诊断的方法是大面积抽查开挖地网，这种方法虽然简单，但盲目性较大、工作量较大、排查速度较慢。为实现在不开挖情况下对接地网的故障进行诊断，目前已有的接地网故障诊断方法主要有导通电阻法、电化学检测法、磁感应强度法以及地表电位法等[2]。导通电阻法是将接地网看成纯电阻网络，通过建立接地网的腐蚀诊断方程，并求解诊断方程得到接地网支路导体的变化值。但接地网各段导体的电阻都比较小，导致导体电阻变化并不明显，使得故障诊断的灵敏度较低[3]。电化学检测法是表征接地网材料腐蚀状态和研究腐蚀机理最有效的手段，但传统的电化学检测系统对测量地网金属的腐蚀状态不够准确，并且测量过程中还存在一些干扰信号和杂散电流，因此电化学检测方法也不能较好地用于接地网的腐蚀诊断[4-5]。磁感应强度法是目前研究接地网腐蚀诊断的热点之一，通过对变电站接地网直接施加激励电流，测量地表面磁感应强度分布，对接地网导体腐蚀和断裂状况进行诊断，但由于变电站内存在很大的噪声干扰，对于信噪比很低的电磁信号很难准确测量，还需要技术上的突破[6-7]。地表电位法也是目前研究接地网腐蚀诊断的热点之一，在接地网拓扑结构一定时，接地网周围的电位分布也将确定，当接地网存在故障时会导致场源发生变化，接地网周围的电场和电位分布也会随着场源的变化而变化，即可根据这一变化确定接地网的故障位置[8-9]。

该文基于地表电位法来对接地网故障进行诊断，但并不仅仅依据地表电位的幅值，而是还考虑到地表电位的相角这一因素，应用地表电位的幅值与相角这2种因素对接地网正常状态与腐蚀变细、腐蚀断裂以及混合故障进行仿真对比研究，从而使接地网故障诊断的准确性有所提升。

1 接地网故障诊断原理及故障模拟

1.1 接地网故障诊断原理

假设电流I通过接地引下线流入接地网，根据恒定电流场理论，参考点选择为无穷远处，运用格林函数原理，即可得到电极泄流电流在任一点P处产生的电位：

(1)

式中：J(Q)为电极表面S在点Q处的泄流电流密度；G(P,Q)为电极几何形状的格林函数。

泄流电流通过接地网流入大地中的总和与从接地极中流入的电流I相等，即

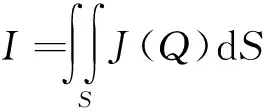
(2)

假设接地网导体上没有电压降，那么边界条件即为

V|Γ=C

(3)

式中：C为常数。

方程式(1)～(3)为计算接地参数的基本方程，数值计算时要采用叠加原理，因此应将接地网中的每个导体都要进行割分，将其看成是点源或者是线源，从而得到n个微段，继而求得每一个微段的电荷密度在一个点上生成的电位，这样就把积分式转化为求和计算。

假设一个长为L的电极，通过该电极所泄流的总电流为I，再把该电极分割成n个微段，第j个微段的长度记为Lj，该微段的中心表示为Oj，该微段所泄流的电流为Ij，则

(4)

(5)

由叠加定理则可求出该电极所泄漏的电流I在P点处的电位：

(6)

式中：G(P,Qj)为以Oj为等效中心的单位点电流源在P点生成的电位。当把G(P,Q)定义为微元段j与场点P之间的互电阻，用Rj,P表示；Vj,P为第j段导体的单位电流源在点P上产生的电压，则

(7)

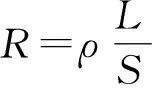
1.2 接地网模型设计

由于对形状规则的接地网已有不少研究，因此此文对不规则接地网进行研究。接地网的模型采用60 m×20 m不规则的方式排列，导体半径为5 mm 的实心铜，接地网埋深为0.8 m，土壤模型为均匀土壤，土壤电阻率为100 Ω·m。接地网模型如图1所示。观测点选取的方向为横向，取接地网模型中30个观测点进行分析。观测点13为电流注入点，其频率为50 Hz，电流大小为4 A。

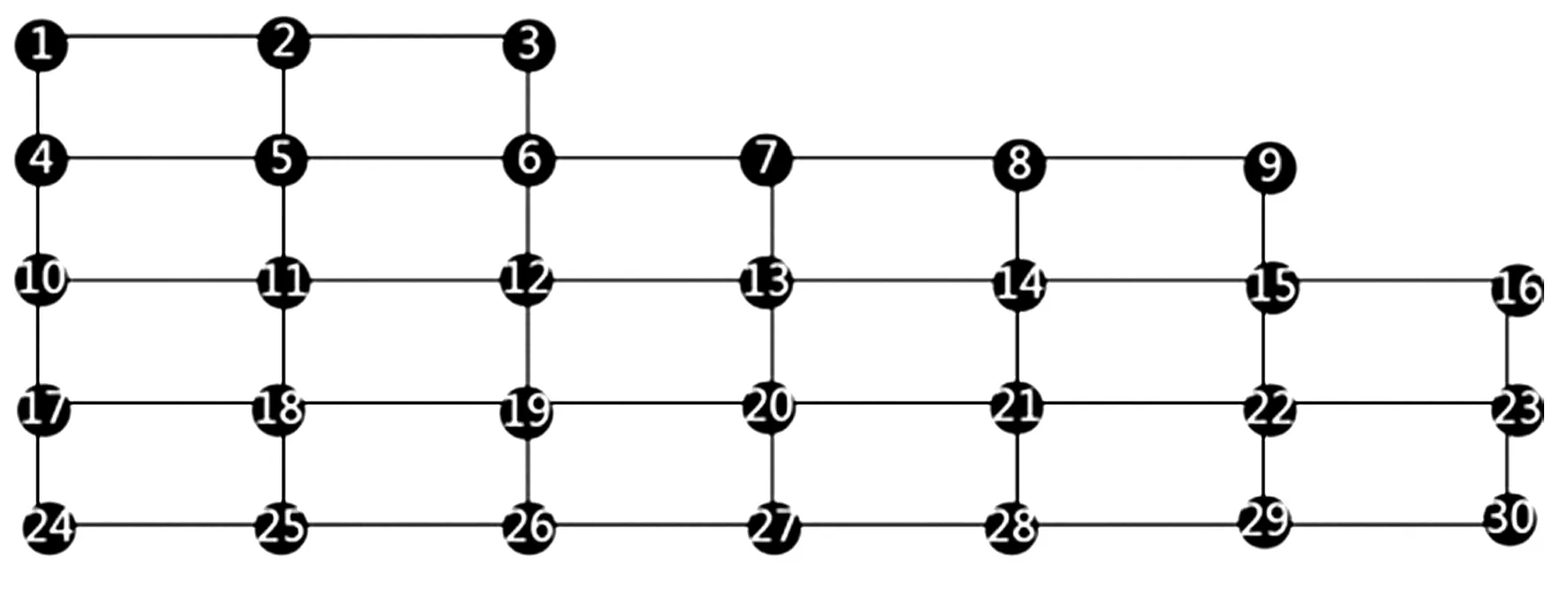
图1 接地网模型图Fig.1 Grounding grid model diagram

1.3 接地网的故障设置

由于接地网常年埋设在地下，其最常见的故障是就是由于腐蚀所带来的接地网导体的腐蚀变细以及腐蚀断裂，因此对导体的腐蚀变细及腐蚀断裂进行仿真研究。故障设置如表1所示。

表1 接地网故障设置Table 1 Grounding grid fault setting

2 结果分析

将无故障接地网观测点的地表电位幅值与相角计算出来，以及将故障状态下接地网观测点的地表电位幅值与相角计算出来，并且用无故障接地网的地表电位幅值减去故障状态下接地网的地表电位幅值，用无故障接地网的地表电位相角减去故障状态下接地网的地表电位相角，从而对无故障与故障接地网地表电位的幅值差与相角差进行分析。

2.1 腐蚀变细

接地网导体的故障分别在观测点6—12之间和20—21之间进行腐蚀变细模拟，模拟方法是将原来导体半径为5 mm的接地体模拟成导体半径为1 mm 的接地体。无故障与故障接地网的地表电位幅值与相角差曲线如图2～3所示。

由图2(a)可见，接地网导体变细以后，故障区域附近的地表电位幅值有明显变化，观测点6和12的地表电位幅值差都明显大于0，但这并不能说明地表电位幅值之差大于0的两观测点之间即为故障区域，因为观测点3的地表电位幅值差也大于0；虽然观测点6和12的地表电位幅值差明显比观测点3的更加突出。由图2(b)可见，观测点3和6的地表电位相角差为同号，而观测点6和12的地表电位相角差为异号。由图3(a)可见，发生故障的区域其地表电位的幅值有明显变化，即观测点20和21的地表电位幅值差都明显大于0。由图3(b)可见，观测点20和21的地表电位相角差为异号。

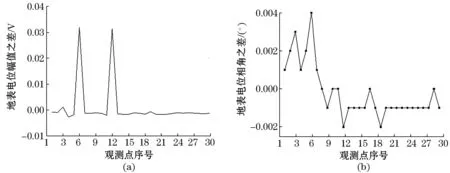
图2 无故障与6—12之间导体变细的地表电位幅值与相角之差Fig.2 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12 thinner conductors

图3 无故障与20—21之间导体变细的地表电位幅值与相角之差Fig.3 The difference in the amplitude and phase angle of ground surface potential between fault-free and 20—21 thinner conductor

2.2 腐蚀断裂

接地网导体的故障分别在观测点6—12之间和20—21之间进行腐蚀断裂模拟，模拟方法是将原先完整的导体模拟为导体中间断裂1 m。无故障与故障接地网的地表电位幅值与相角差曲线如图4～5所示。

由图4(a)可见，接地网导体断裂后，故障区域附近的地表电位幅值有明的变化，观测点6和12的地表电位幅值差都明显大于0，同样也不能说明地表电位幅值之差大于0的两观测点之间即为故障区域，因为观测点3的地表电位幅值差也大于0;虽然观测点6和12的地表电位幅值差还是明显比观测点3的突出。由图4(b)可见，观测点3和6的地表电位相角差为同号，而观测点6和12的地表电位相角差为异号。由图5(a)可见，发生故障区域的地表电位幅值有明显变化，即观测点20和21的地表电位幅值差都明显大于0。由图5(b)可见，观测点20和21的地表电位相角差为异号。

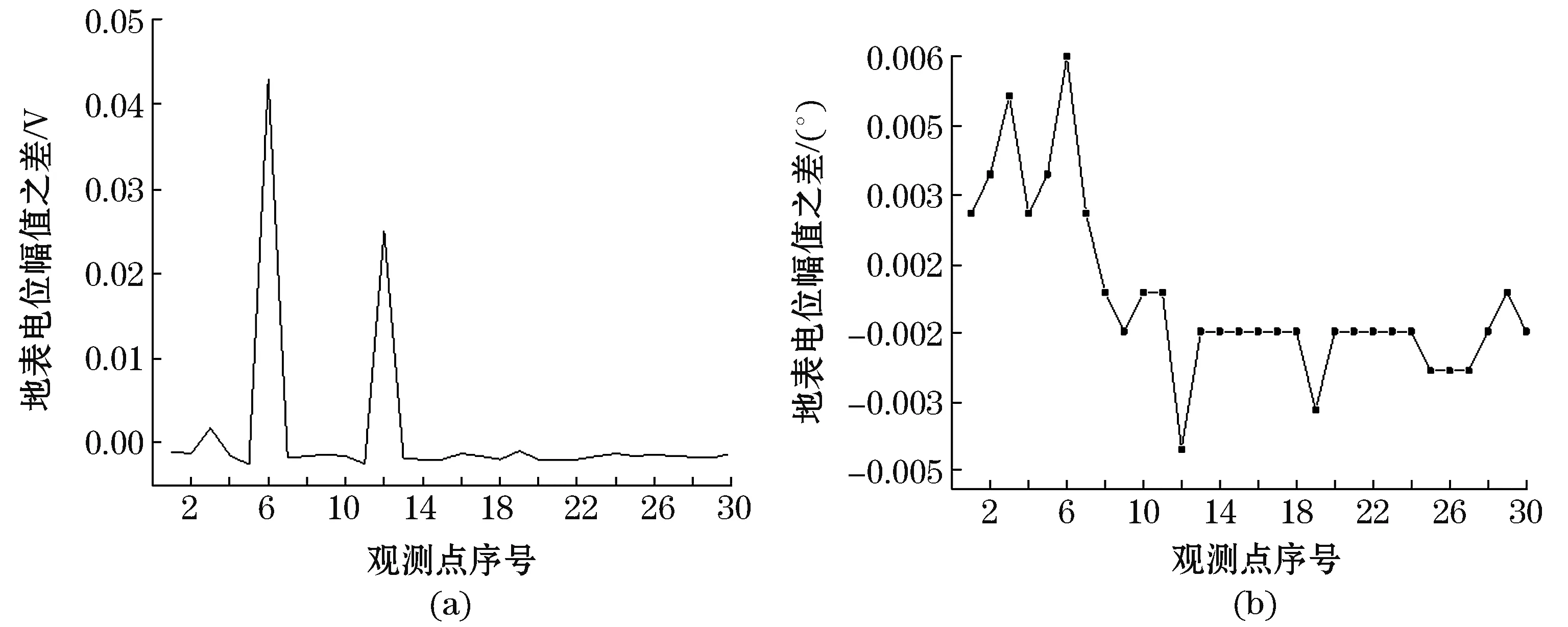
图4 无故障与6—12之间导体断裂地表电位幅值与相角之差Fig.4 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12 conductor fracture

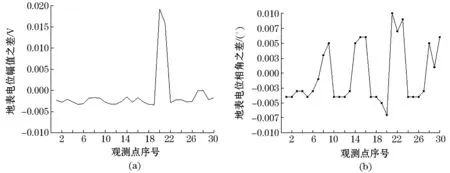
图5 无故障与20—21之间导体断裂地表电位幅值与相角之差Fig.5 The difference in the amplitude and phase angle of ground surface potential between fault-free and 20—21 conductor fracture

因此，由上述两个不同的单一故障可以得出，在观测点地表电位幅值差都大于0且两者之间的地表电位相角差为异号时，才能准确诊断出故障区域。

2.3 混合故障

上文仿真模拟了单一故障的状况，但实际中还存在大量的多个故障的现象，以2种故障混合进行研究。接地网导体的故障分别在观测点6—12之间和20—21之间进行混合故障的模拟，无故障与故障接地网的地表电位幅值与相角差曲线如图6～9所示。

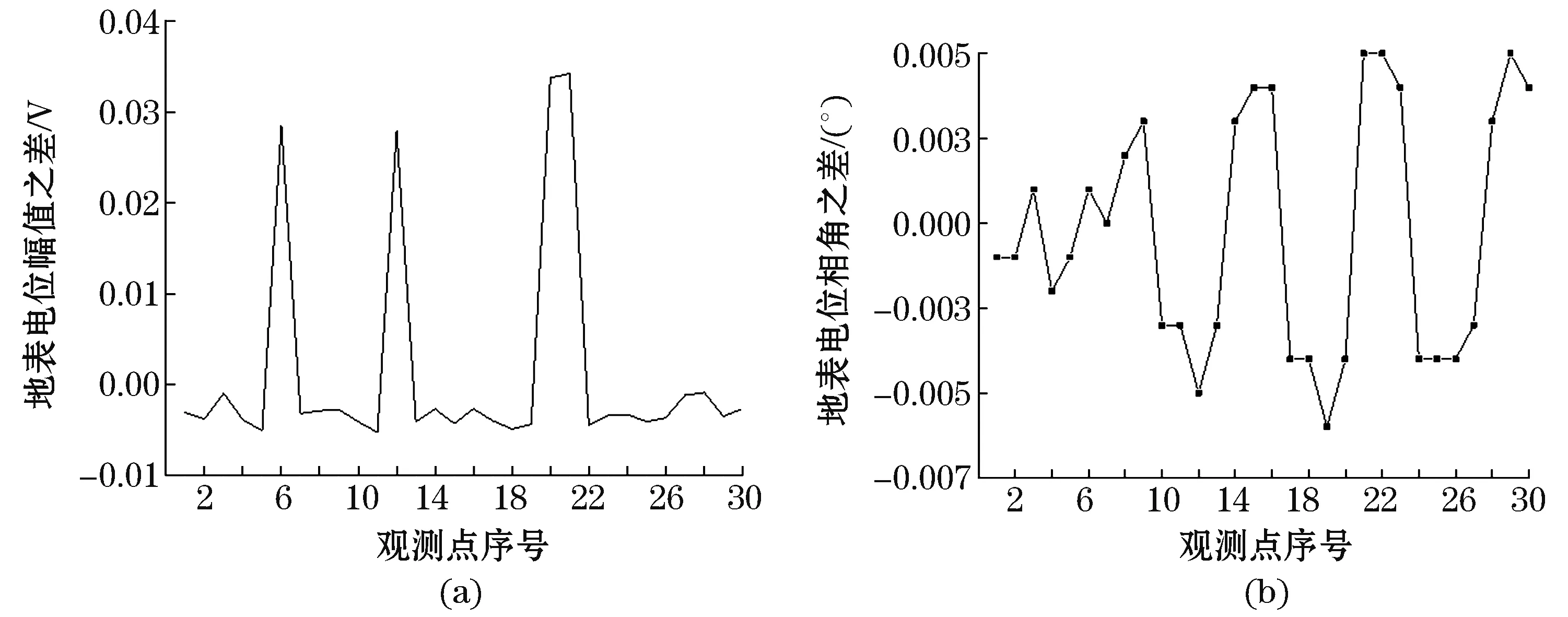
图6 无故障与6—12变细、20—21变细地表电位幅值与相角之差Fig.6 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12，20—21 thinner conductor

图7 无故障与6—12断裂、20—21变细地表电位幅值与相角之差Fig.7 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12 conductor fracture，20—21 thinner conductor

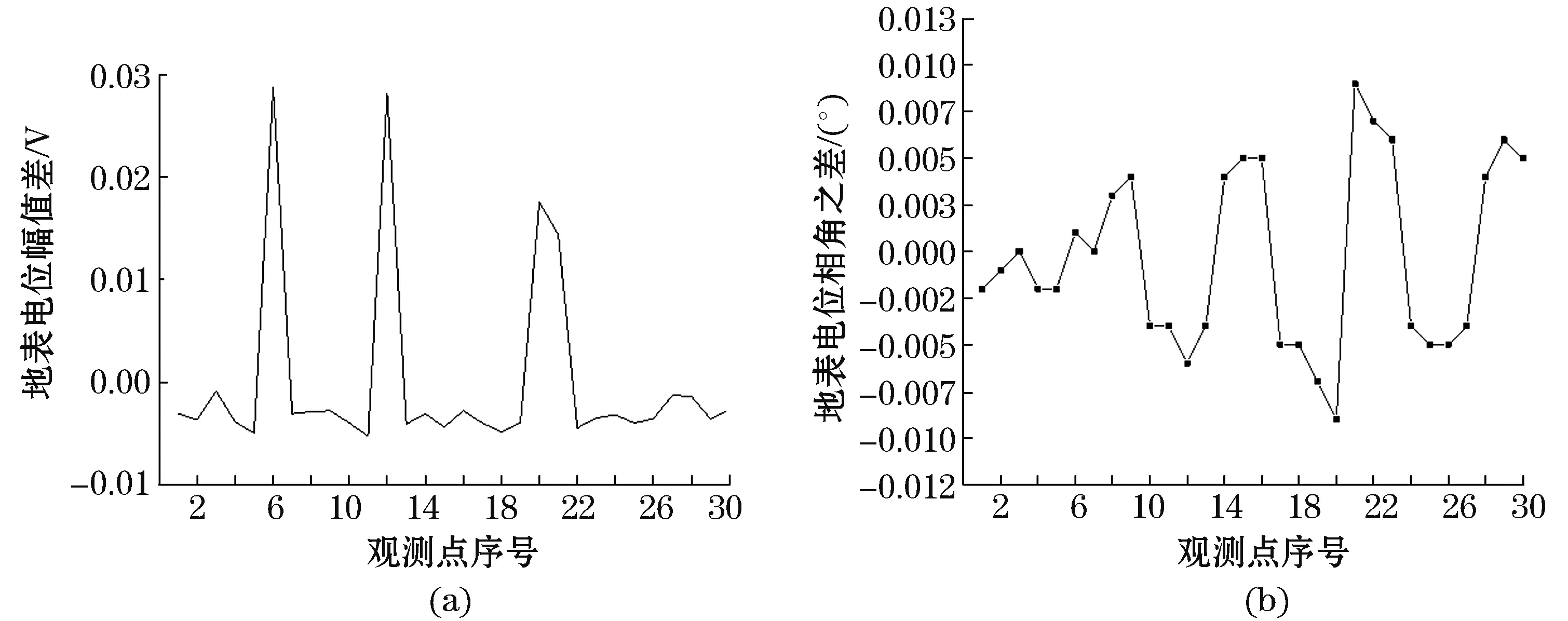
图8 无故障与6—12变细、20—21断裂地表电位幅值与相角之差Fig.8 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12 thinner conductor，20—21 conductor fracture

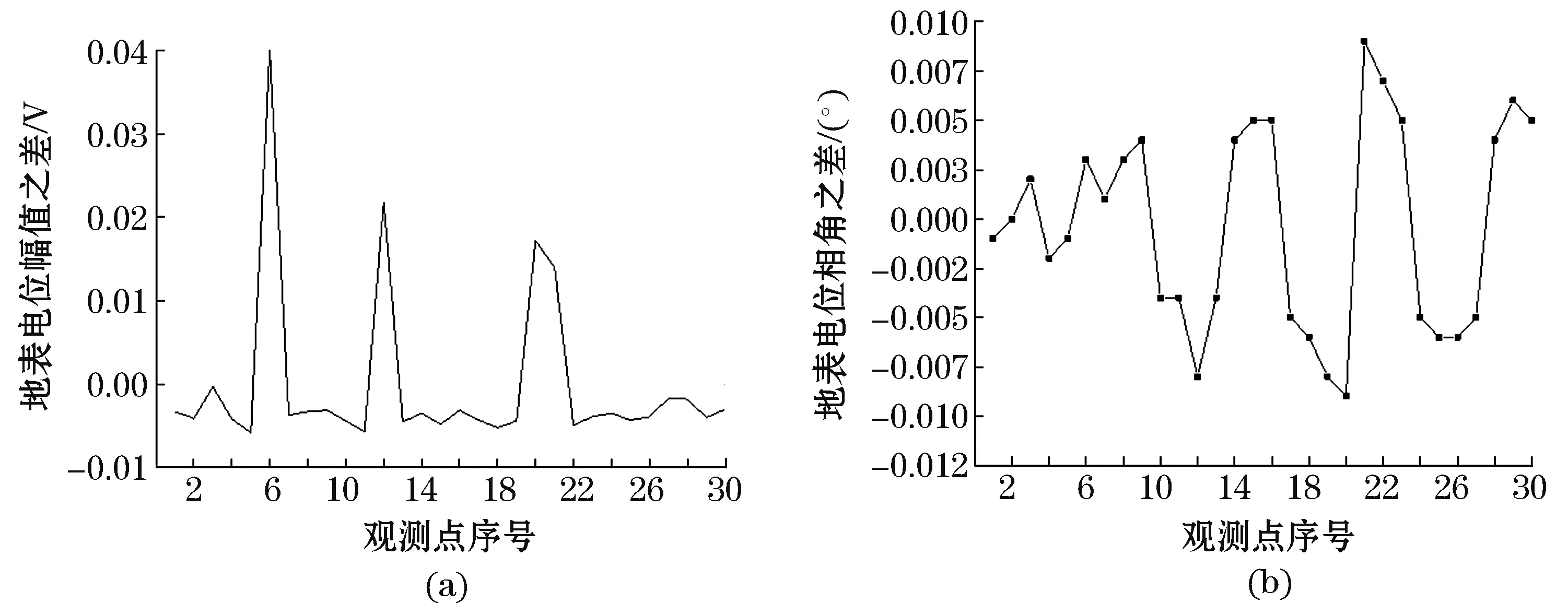
图9 无故障与6—12断裂、20—21断裂地表电位幅值与相角之差Fig.9 The difference in the amplitude and phase angle of ground surface potential between fault-free and 6—12，20—21 conductor fracture

由图6～9可见，接地网存在两种故障以后，故障区域的地表电位幅值都有较为明显的变化，观测点6和12以及观测点20和21其地表电位幅值差都大于0，而且观测点6和12的地表电位相角差为异号，观测点20和21的地表电位相角差也为异号。

3 接地网诊断分析

根据所有曲线图(a)的计算结果，最大幅值差和相角差见表2、表3。

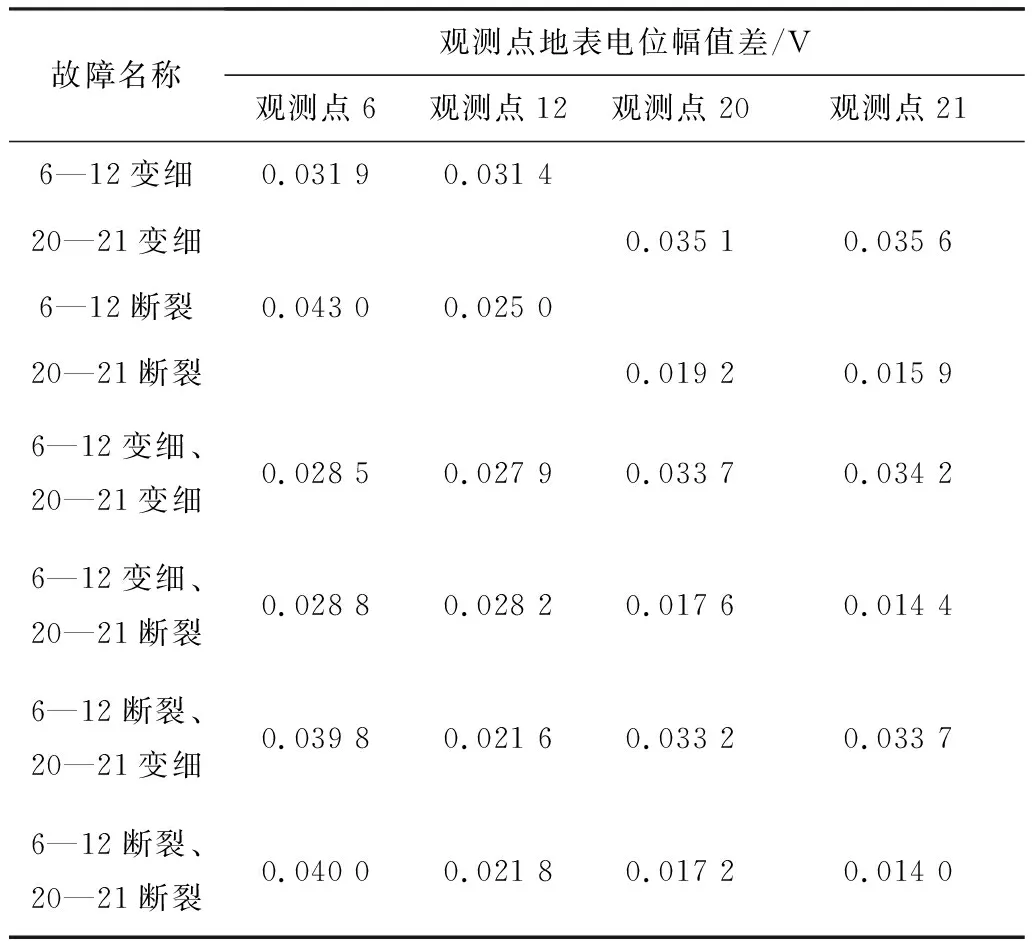
表2 接地网故障区域地表电位幅值差Table 2 Ground potential amplitude difference in the fault area of grounding grid

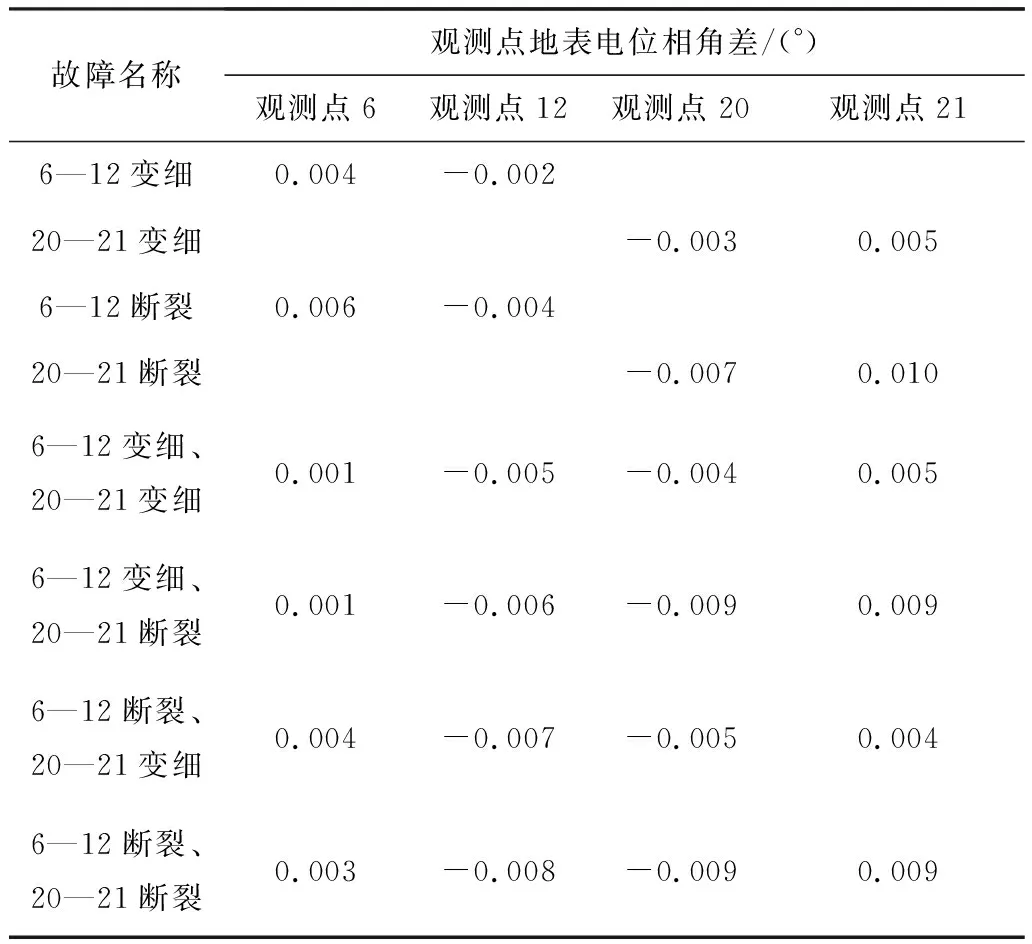
表3 接地网故障区域地表电位相角差Table 3 Groundphase angle difference in the fault area of grounding grid

由表2可得出，无论是接地网导体腐蚀变细还是腐蚀断裂故障，观测点6的地表电位幅值差的数值都比观测点12的地表电位幅值差的数值要大，并且在接地网腐蚀断裂故障中其数值要大的更加明显，因此在故障导体方向与选取观测点方向垂直时，观测点离电流注入点越远则地表电位幅值下降越大。而在接地网导体腐蚀变细故障中，观测点20的地表电位幅值差的数值都比观测点21的地表电位幅值差的数值要略小一些。但在接地网导体腐蚀断裂故障中，观测点20的地表电位幅值差的数值都比观测点21的地表电位幅值差的数值要明显大一些。接地网混合故障中观测点的地表电位幅值差要比同样故障条件下2个单一故障中观测点的地表电位幅值差要小。这说明混合故障会使地表电位幅值变化的幅度降低。

由表3可得出，接地网混合故障中观测点的地表电位相角差要比同样故障条件下2个单一故障中观测点的地表电位相角差要小一些。这说明混合故障会使地表电位相角变化的幅度也会有所降低。

从所有曲线图(b)的计算结果中可见，接地网故障区域的相角变化最为剧烈，也就是说故障区域相角之间的差值要比无故障区域相角之间的差值要大。

4 结 语

1)在应用地表电位对接地网故障进行诊断时，当观测点的地表电位幅值差都大于0且两者之间的地表电位相角差为异号时，此观测点之间的区域为故障区域。

2)仿真所注入的电流为4 A，在实际应用时可提高电流的大小，从而使地表电位的幅值差有所增大，以利于提升故障辨识精度。

3)在应用地表电位的相角差来诊断故障时，也需注意在实际应用时，相角测量的精度是否能够达到，还需要进一步研究。