生产周期和更新换代影响下的商品微分动力模型分析
2021-12-28高德宝魏玉芬
高德宝,魏玉芬,朱 焕
(黑龙江八一农垦大学理学院,黑龙江大庆 163319)
§1 引言
很多商品需要生产时间,比如汽车和商品房等.一般地情况下,现在的商品供给量是过去的一段时间内生产出来的,也就是说商品的供应具有迟滞性[1-3].当商品生产出来时,供给量可能与当时的需求量不相符,由此产生供给量与需求量的博弈,两者的博弈过程主要表现为商品价格的动态变化过程.商品的交易是以价格为媒介的.商品的供给量会随着价格的升高而增加,亦会随着价格的降低而减少.厂家以价格与成本之差为利润提供商品供应量.在满足自身需求的基础上,顾客以价格为度量购买商品.当然价格越低,销售量越多,即需求量越多.简而言之,厂家以价格为度量提供商品供给量,价格过高则需求量少,价格偏低,需求量会增多.这种关系就是“捕食-被捕食”[4-8]关系.具体地说,供给量捕食价格,价格捕食需求量.
一些商品的更新换代比较频繁.比如手机经历了1G,2G,3G,4G和现如今的5G时代,将来也必将会发展到6G时代.商品更新换代的初始,新产品的价格一般会瞬时增高(比如现在5G手机价格普遍高于4G的价格),这在生物数学[9-10]理论中称之为脉冲[11-13],但价格会随着时间地流逝而逐渐进入合理的波动范围内.
生物数学的主要内容是应用微分方程理论研究种群生态问题和传染病问题.因为微分方程的一些理论也能比较贴近实践地描述经济运行的动态关系,所以很多经济模型可以借助微分方程构建并加以研究.例如国外学者[14-17]利用时滞微分方程构建商业周期模型,同时研究时滞对经济运行稳定性的影响,最后得出非线性投资函数,非线性储蓄函数和时滞是导致经济模型产生周期性波动的原因.另外,徐飞[18]运用类似的思路建立了综合国力模型和金融企业竞争模型,研究了两个模型的稳定性及周期解的存在性.脉冲微分方程在经济模型中的应用尚不多见,但在生物数学模型中应用较多.
上述的经济模型主要以金融投资和企业竞争为核心,本文的工作与他们的不同.本文利用时滞微分方程构建供给量,价格和需求量之间关系的数学模型,其中时滞代表生产周期.而用脉冲微分方程描述产品更新换代后对商品供需关系的扰动作用.通过分析供给量,价格和需求量之间的动态关系,希望能够为探索商品的动态运行规律添砖加瓦.
§2 生产周期影响下商品微分动力模型的构建与分析
一般地情况下,商品的供给量随着价格的变化而变化,价格高时,供给量会增加,价格低时,供给量会减少.但是,多数商品的生产需要一个周期,所以其供应量的实现具有时滞性.价格能够实时地反映供应量与需求量之间的关系.当价格低时,需求量会增加,当价格过高时,需求量会减少.一般地情况下,商品的需求量与其价格之间反向变动,商品的供给量与价格之间正向变动.因此,本文假设供给捕食价格,价格捕食需求,商品的供应具有时滞性.
假设t时刻,商品的需求量,价格和供给量分别为D(t),P(t),S(t −τ),其中τ表示商品的生产周期.根据上一段的分析,假设需求量与价格之间的功能性反应函数均具有HollingⅡ型功能性反应[9],价格与供给量之间具有线性功能反应.另外受消费人数的限制,需求量具有密度制约性[9],并且需求不完全依赖供给和价格而存在.综上分析和假设,需求,价格和供给之间捕食关系如图1所示,则仅受生产周期影响的商品微分动力学模型为
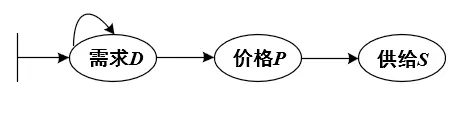
图1 需求,价格和供给之间的捕食关系图
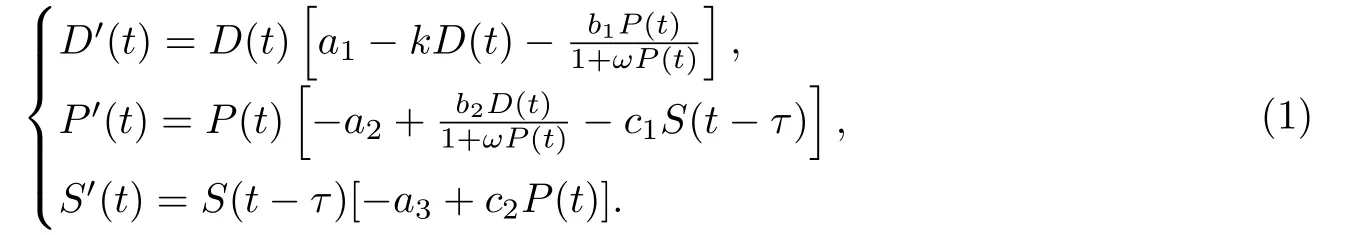
其中a1,a2,a3,b1,b2,c1,c2,ω,k均为正数.各系数的经济学意义如表1所示.

表1 参数的经济学意义
模型(1)在(−τ,0]内的初始条件满足

基于问题的实际意义,模型(1)的可行域为

易知模型(1)右侧的函数具有光滑性,因此模型(1)满足初始条件的解是存在的并且唯一.
定理1对于任意以D(0)>0,P(0)>0,S(0)>0为初值的模型(1) 的解恒大于零.
证首先证明当S(0)>0时,S(t)>0.否则存在t1∈(0,+∞),使得S(t1)≤0.根据零点定理可知存在t0∈(0,t1]使得S(t0)=0.
又由(D,P,S)=(0,0,0)为模型(1)的平凡解,这与模型(1)解的唯一性相矛盾.故S(t)>0.
模型(1)的前两个方程等价于以下两个方程
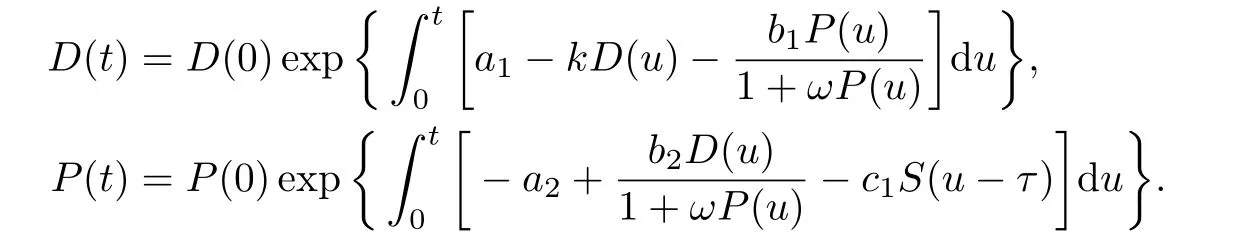
显然,当D(0)>0,P(0)>0时,D(t)>0,P(t)>0.
综上所得,定理1的结论成立.
由定理1可知,商品的需求量,价格和供给量均大于零,这与实践相吻合.
定理2对于模 型(1)的任 意解(D(t),P(t),S(t)),存在正数MD,MP,MS,T0, 当t >T0时,D(t)≤MD,P(t)≤MP,S(t)≤MS.
证令,则有

根据定理1的结论和(2)的假设可知:当t ∈(0,+∞)时,
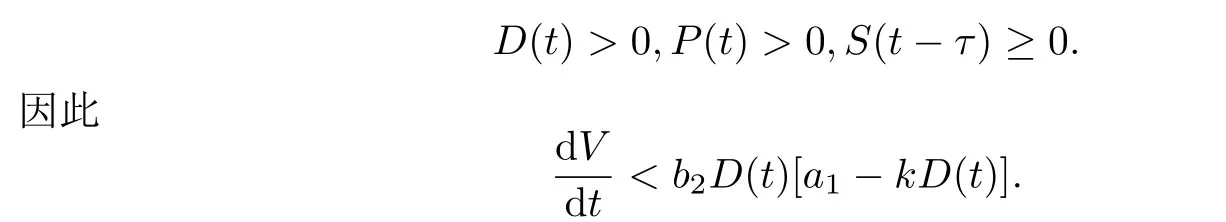
由比较定理[19]可知存在T0>0,当t>T0时,.进一步地计算可得

定理2的结论说明,商品的需求量,价格和供给量都是有上限的.实践中,受消费人群的限制,需求量总是有限的.比如刚需的商品房,平均每人最多需要一套.商品价格需要在消费者的承受范围内,否则无法购买商品.因此,商品的价格是有限的.受生产能力的限制,商品的供给量是有限的.若供给量远远大于需求量,可能会产生两个后果:一是商家无利可图;二是该商品经济崩盘,例如美国的房地产危机.因此,供给量总是有限的.
定理3若条件

成立,则模型(1)存在唯一的正平衡点(D∗,P∗,S∗),其中

证模型(1)的正平衡点满足方程组

通过求解方程组(3),易知:若条件H1,H2成立,则D∗,P∗,S∗均为正数.
正平衡点的经济学意义就是供需平衡时,需求量,价格和供给量所处的平衡状态.
定理4若模型(1)满足条件H1,H2和条件

则存在τ0>0,使得模型(1)所对应的正平衡点(D∗,P∗,S∗),当0≤τ <τ0时,局部渐近稳定;当τ=τ0时,模型(1)在点(D∗,P∗,S∗)产生Hopf分支;当τ >τ0时,(D∗,P∗,S∗)是不稳定的.
证模型(1)在(D∗,P∗,S∗)的变分矩阵J(D∗,P∗,S∗)为
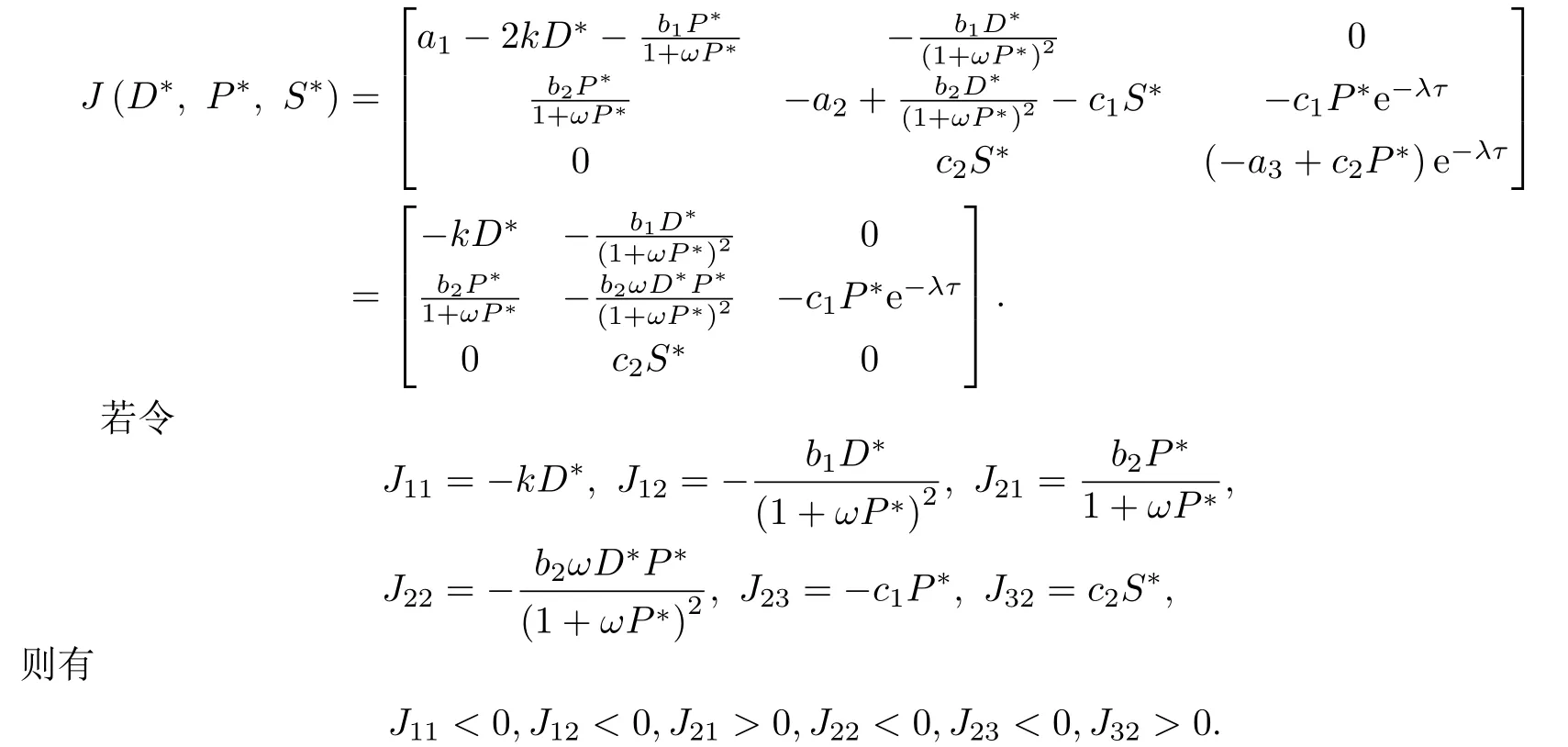
特征方程F(λ)=|J(D∗,P∗,S∗)−λE|=0的表达式为
当τ=0时,特征方程(4)变为
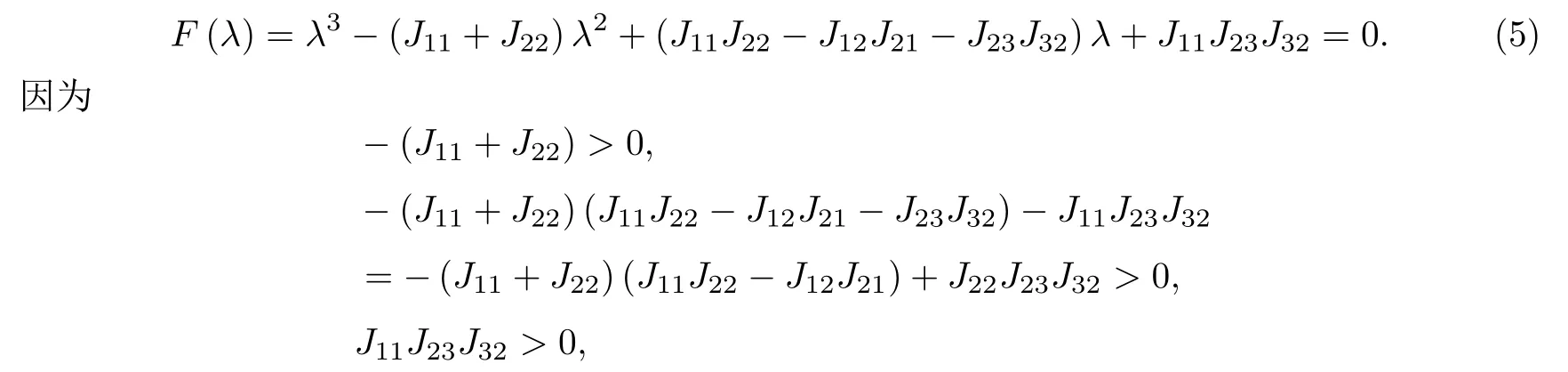
根据Routh-Hurwitz定理[9]可知特征方程(5)的特征根均具有负实部.由Hurwitz准则[9]知:当τ=0时,正平衡点(D∗,P∗,S∗)是局部渐近稳定的.
当τ >0时,设λ=mi(m>0)是特征方程(4)的一纯虚根,则m满足
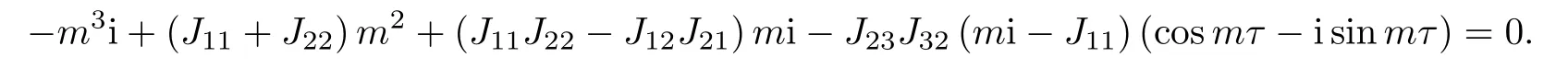
进一步地可得

因此(m2)至少有一正根,进而特征方程(4)存在一对纯虚根±m0i.将其代入方程组(6)有
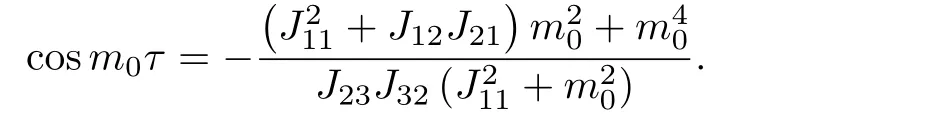
由上式可得与ω0对应的τn,

取τ0是上式产生纯虚根的最小正值,则当τ <τ0时,正平衡点(D∗,P∗,S∗)仍然保持稳定.
令λ=λ(τ),代入方程(4),并在其两边对τ求导,有
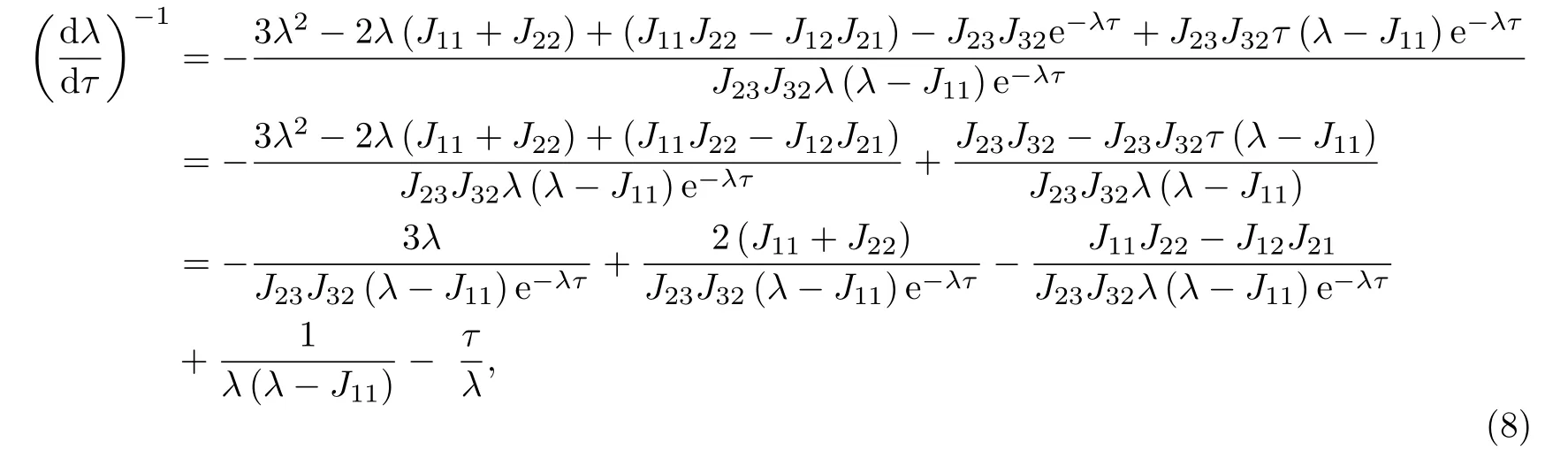
将λ=m0i,τ=τ0代入(8)式得
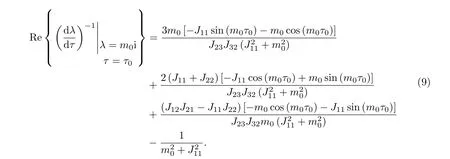
因为m0,τ0满足方程组(6),所以有
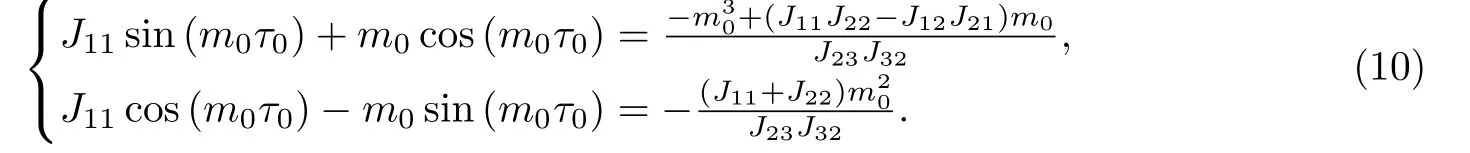
将(10)式代入(9)式并整理得

因为m0满足方程(7),所以(11)式可变换为
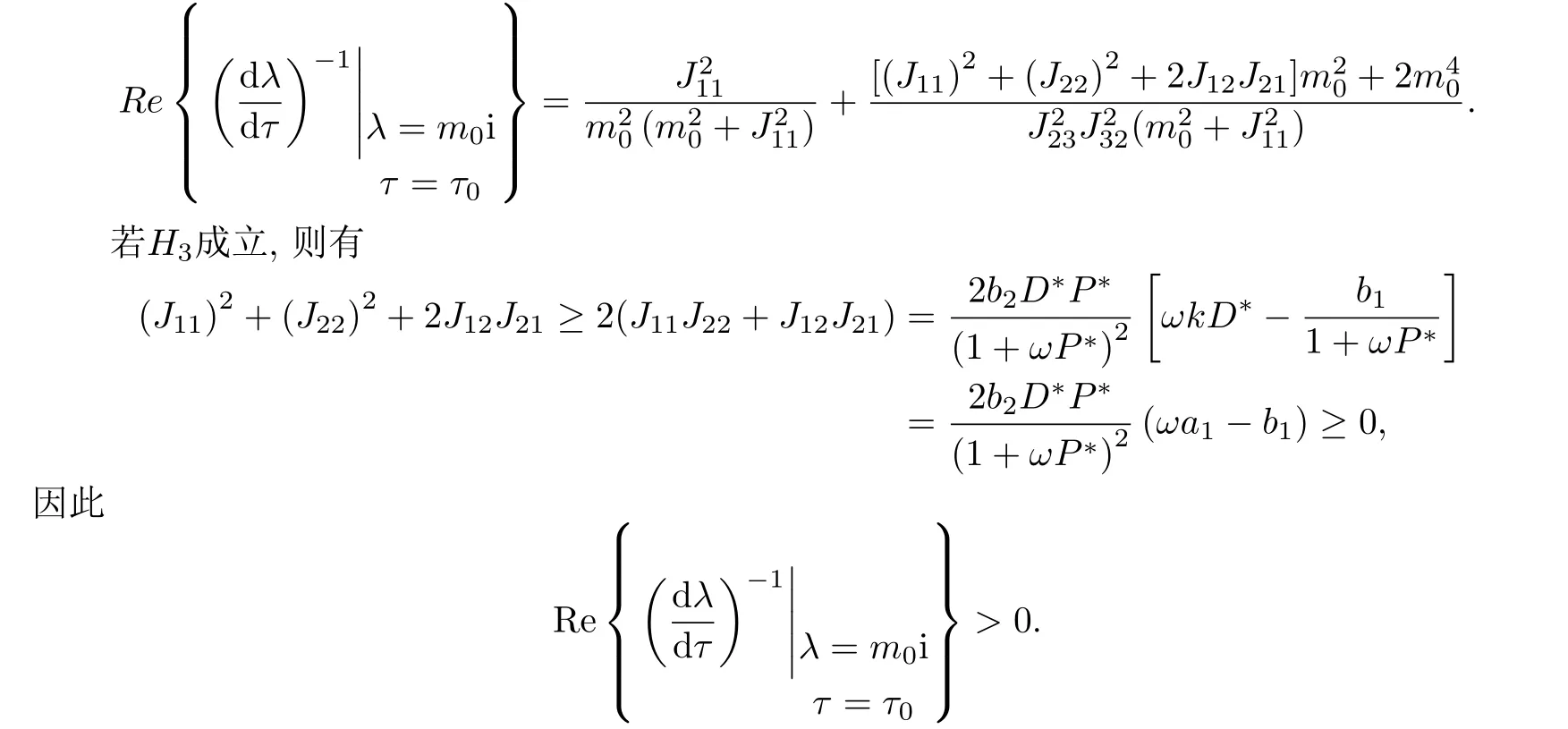
由Butler引理[20]知:当τ=τ0时,模型(1)在正平衡点(D∗,P∗,S∗)产生Hopf 分支;当τ <τ0时,正平衡点(D∗,P∗,S∗) 局部渐近稳定;当τ >τ0时,正平衡点(D∗,P∗,S∗)不稳定.
定理4给出正平衡点局渐近稳定的平衡条件主要与生产周期τ有关.当τ <τ0时,需求量,价格和供给量将会动荡地趋于平衡状态;当τ=τ0时,需求量,价格和供给量将会周而复始地围绕正平衡点波动;当τ >τ0时,需求量,价格和供给量没有平衡状态.
为验证上述结论的正确性,取不同的系数和不同的时滞τ对模型(1)进行数值模拟.首先,取系数

经计算,可验证上面的系数满足条件H1−H3,模型(1)的正平衡点和m0,τ0分别为
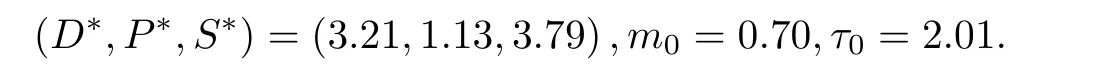
取初值(D,P,S)=(2,1,2).当取τ=1.8<2.01时,正平衡点是局部渐近稳定的.模型(1)收敛的相图分别如图2与图3所示.

图2 模型(1)局部渐近稳定的平面相图

图3 模型(1)局部渐近稳定的空间相图
最后,取系数
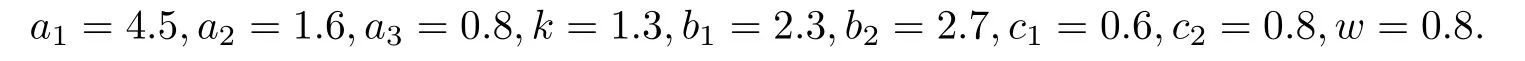
模型(1)的正平衡点和m0,τ0分别为

取初值(D,P,S)=(1,1.5,1),τ=2.2≈2.19=τ0,模型(1)围绕正平衡点产生周期解,其相图如图4和图5所示.

图4 模型(1)存在周期解的平面相图
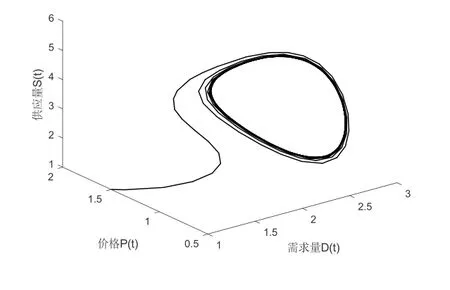
图5 模型(1)存在周期解的空间相图
§3 生产周期与更新换代叠加效应影响下的商品动态关系分析
商家为了提高其商品在市场上的竞争力,需要不断地对其进行更新换代,例如iPhone手机已更新到12代.上一节的内容仅考虑了生产周期对供应量,价格和需求量的影响.若商品的更新换代已完成,则必定会对商品产生一定程度的影响.更新换代的商品是为了替代没有竞争力或竞争力不高的前代商品,因此商品的总供应量基本不会发生改变;同时基于消费者的猎奇心理和商家的营销手段,总需求也会增加一些;在商品更新换代初始时间内,新商品的价格也会增加一些(例如现在的5G手机价格).
为简化问题,假设商品的更新换代时间具有周期性,即kT(k=1,2,···)时刻发生.假设kT时刻,商品的价格增加了p0,需求量增加了d0,则生产周期与更新换代叠加效应影响下的商品动态关系模型如下所示.
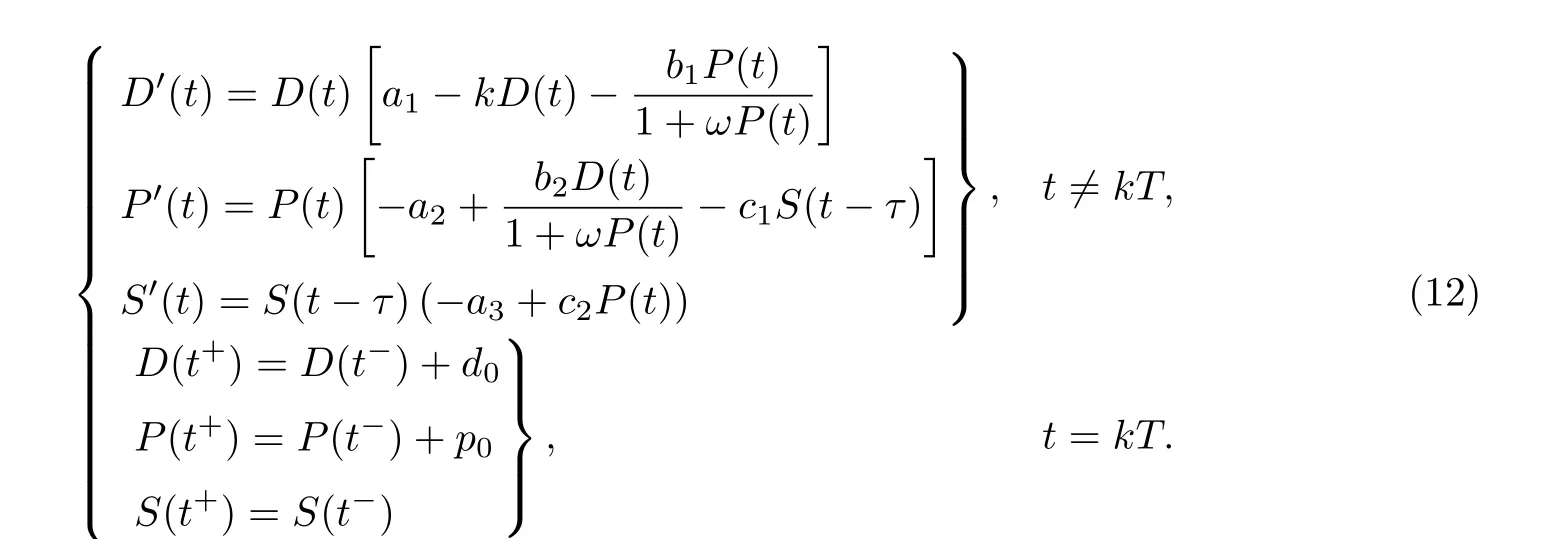
其中d0>0,p0>0.
定理5对于模型(12)的任意解(D(t),P(t),S(t)),存在MD >0,MP >0,MS >0,T0>0,当t>T0时,D(t)≤MD,P(t)≤MP,S(t)≤MS.
证仍取定理2中的V(t)=,则当t≠kT时,存在T0>0,当t>T0时,

根据模型(12)的第3-6个方程,当t=kT >T0时,可得
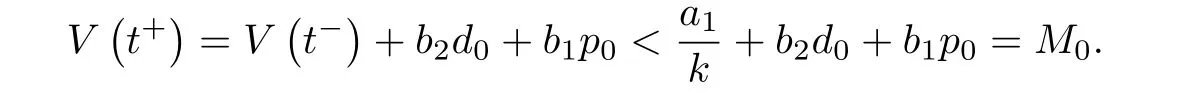
综上分析可得,当T0 定理5的结论表明无论更新换代多少次,需求量,价格和供给量都会有上限.例如多数的电子信息产品,因为顾客的数量是有限的,需求量必然有限;随着生产技术的提高,电子商品的生产成本会降低,所以价格会逐步的减少;若供给量过多,供大于求,则商家的利益得不到保障,因此,供给量只能是有限的. 引理1[21]考虑下面的脉冲微分模型 其中d,µ>0.那么模型(13)存在惟一的正周期解. 定理6当ωa1−b1>0时,存在mD >0,mP >0,T1>0,当t>T1时,对于模型(12) 的任意解(D(t),P(t),S(t)),有D(t)≥mD,P(t)≥mP. 证因为 根据比较原则,存在t1>0,当t>t1时 根据引理1和比较原则可得,对于模型(14)的任意解有 取mP={P∗exp(−m1(t −kT))},t ∈((k −1)T,kT],k ∈Z+,则存在t2>0,当t>t2时,P(t)≥mP. 取T1=max{t1,t2},则当t>T1且ωa1−b1>0时,D(t)≥mD,P(t)≥mP. 价格不能低于成本,否则商家无利可图.为了保证正常的生存,需求量是有下界的,比如生物对水的需求量.这两个实际情况与定理6 的结论相吻合.不过,供给量可能会出现断货或接近于断货的情形,这种情况时有发生. 定理7当ωa1−b1>0时,模型(12)存在周期解. 证取T2=max{T0,T1},根据定理5和定理6可知:当ωa1−b1>0且t >T2时mD ≤D(t)≤MD,mP ≤P(t)≤MP, 0≤S(t)≤MS. 根据确界原理和函数D(t)的连续性可知 作映射 根据Brouwer不动点定理[22],至少存在一点t0∈[T2, +∞),使得D(t0)=D(t0+T).则D(t)至少有一个以T为周期的正周期解.同理可证:P(t),S(t)均至少存在一个以T为周期的正周解. 综上可得当ωa1−b1>0时,模型(12)存在正周期解. 定理7表明:商品周期性地更新换代之后,需求量,价格和供给量必将会周期地发生波动. 取T=20,τ=2.1,d0=0.1,p0=0.4,其余各项系数与图2中的各项相同.数值仿真结果如图6所示. 图6 模型(12)存在周期解的平面相图 从图6可以得出,当更新换代周期地发生时,前两个周期内,需求量,价格和供给量由无规则波动逐渐地趋于规律化.从第3个周期开始,三者完全遵循周期性波动.这与定理7的结论是一致的.由图6中的前两张图可以看出,尽管更新换代伊始,需求量会稍有提高,价格也会偏高一些,但是它们会逐渐回归到正常的波动范围内. 当仿真参数发生改变时,不同的是:需求量,价格和供应量无规律波动的周期个数可能不同.相同的是:从某一个周期开始,三者都会周期地发生波动. 根据具有生产周期商品的需求量,价格和供给量之间的捕食与被捕食关系,还有更新换代对商品供求关系的的影响,本文建立了两个数学模型:时滞微分方程模型和脉冲微分方程模型.利用Hopf分支定理,得到:需求量,价格和供给量渐近稳定收敛于正平衡点的充分条件和它们会循环往复地围绕正平衡点作周期性波动的充分条件.在ωa1−b1>0条件下,当生产周期和周期性更新换代叠加影响时,商品的需求量,价格和供给量必然有上下限;同时,它们必将会在某一时刻之后作周期性波动. 本文工作的优点如下. (1)根据需求量,价格和供给量之间相互作用关系,建立了符合商品动态运行实践的数学模型; (2)两个数学模型很好地解释了一些特殊的商品经济现象; (3)两个数学模型能够为商家在采购,生产和销售中的决策提供有价值的参考. 本文工作没有考虑到随机因素的影响,也没有商业实践数据的支撑,进而无法确定参数.笔者希望这些问题能够在未来的工作中得到有效解决.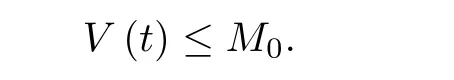

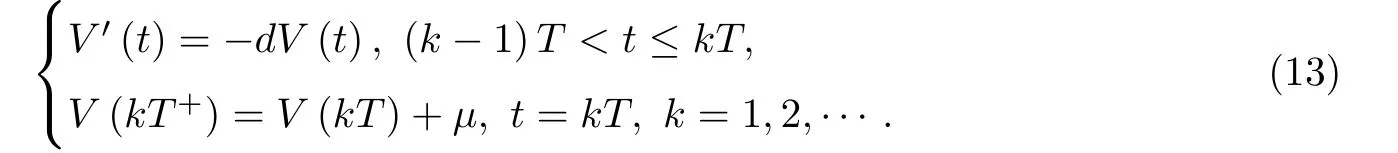
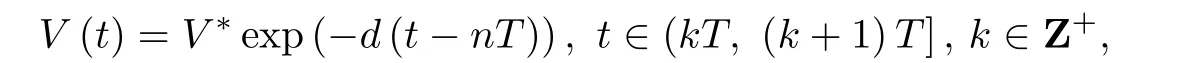
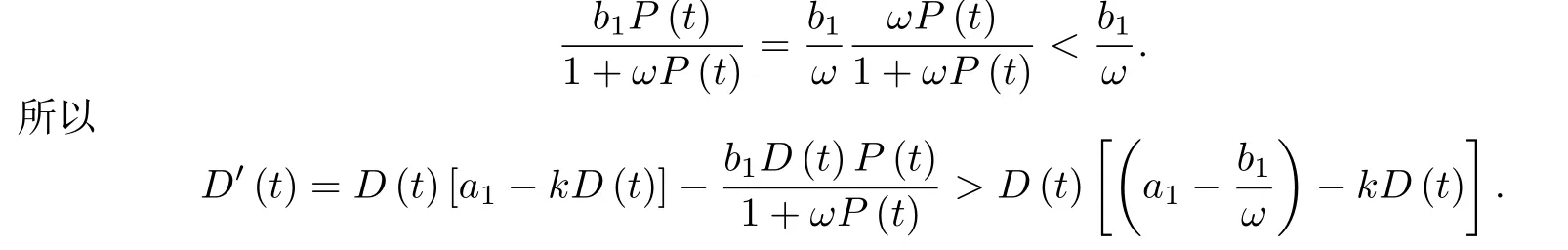
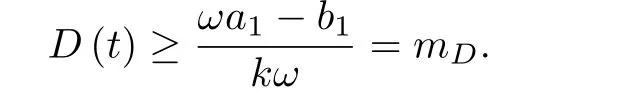
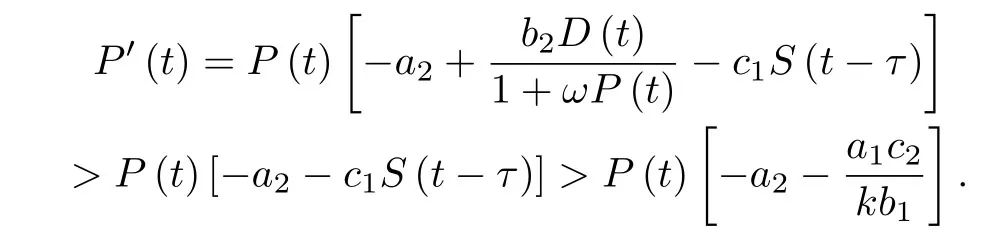

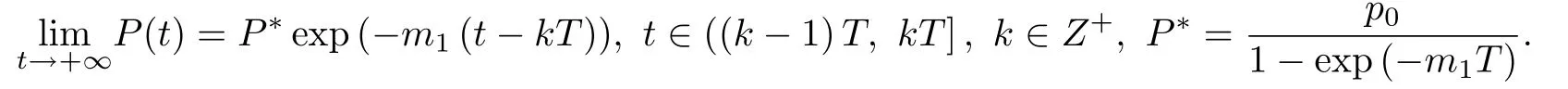

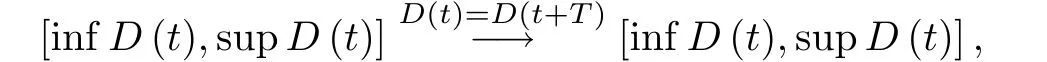

§4 结语
