城轨牵引供电系统逆变回馈装置的定容选址
2021-12-28潘卫国李群湛
刘 炜 ,张 浩 ,张 戬 ,李 由 ,潘卫国 ,李群湛
(1. 西南交通大学电气工程学院,四川 成都 610031;2. 北京全路通信信号研究设计院集团有限公司,北京
100071)
逆变回馈装置不但可以有效利用城轨列车再生制动能量,还可以改善城轨牵引供电系统网压水平,近些年国内广泛投入使用[1-2]. 逆变回馈装置容量配置及安装位置是影响系统节能效果评估的重要因素,装置选址定容等问题是现阶段亟需解决的问题之一[3-4].
针对城轨再生制动能量利用装置定容选址的优化问题,是现阶段研究的热点. 文献[5]根据地铁列车全线对向行驶时供电臂和走行轨等效电阻的损耗功率最小对逆变回馈装置进行选址,由于实际全线牵引变电所数量多、计算量大,该法收敛速度较慢.文献[6-7]考虑超级电容储能装置的节能电量与投资成本,同时优化装置能量管理策略控制参数,结合城轨供电仿真平台与遗传算法,实现了多目标同时优化. 多目标优化问题受各个目标量纲属性不同的影响,很难找到一组同时满足所有目标最优的解,通常存在一个Pareto 最优解集,其各组非劣解之间互不支配,无法在优化任何目标的同时不削弱其他目标[8].这一多目标优化问题的求解思想常与智能算法结合以搜索非劣解集.
在利用遗传算法求解多目标优化问题上,相关文献展开了研究. 吴广宁等[9]在牵引变电所接地网优化设计上对传统遗传算法做出了改进,添加适应度函数并采用自适应算法根据适应度值动态调整交叉概率和变异概率,避免算法进入局部最优解. Deb等[10]为进一步提高遗传算法的计算效率和鲁棒性,在NSGA (non-dominated sorting genetic algorithm)的基础上提出了一种带精英策略的快速非支配排序遗传算法(fast NSGA-Ⅱ). 文献[11-12]验证了NSGA-Ⅱ相对传统遗传算法和并行粒子群算法具有计算精度高、收敛速度快的优点.
本文首先分析了含逆变回馈装置的系统级节能指标,并建立城轨逆变回馈装置定容选址多目标优化模型,其次将考虑逆变回馈装置周期性间歇工作制的城轨交直流混合潮流算法与NSGA-Ⅱ结合求解多目标函数的Pareto 解集,采用基于信息熵的序数偏好法(technique for order preference by similarity to ideal solution,TOPSIS)归一化各目标函数值,计算相对理想距离,进而在Pareto 解集中筛选出逆变回馈装置选址定容最优方案. 最后以广州某地铁线路为例进行仿真分析,验证算法有效性.
1 优化模型
1.1 目标函数
从逆变回馈装置的投资成本以及逆变回馈装置对城轨牵引供电系统节能效果两个角度,建立逆变回馈装置定容选址优化模型.
1) 逆变回馈装置投资成本. 受地铁线路坡度及曲线信息影响,列车在各站间产生的再生制动能量不同,考虑逆变回馈装置经济投资因素,应在各牵引所安装不同容量的逆变回馈装置. 选择全线逆变回馈装置优化容量配置投资总成本的相反数作为目标函数f1(X),如式(1).

式中:cEFS,i为第i个牵引所内逆变回馈装置投资成本;Nall为全线逆变回馈装置投入总数量;X为全线各牵引所逆变回馈装置容量配置集合;xi为第i个牵引所内逆变回馈装置容量.
2) 系统级节能率. 全线不安装逆变回馈装置的城轨牵引供电系统作为参考系统,其系统能量流向如图1 所示. 安装逆变回馈装置后,城轨牵引供电系统能量流向如图2 所示.
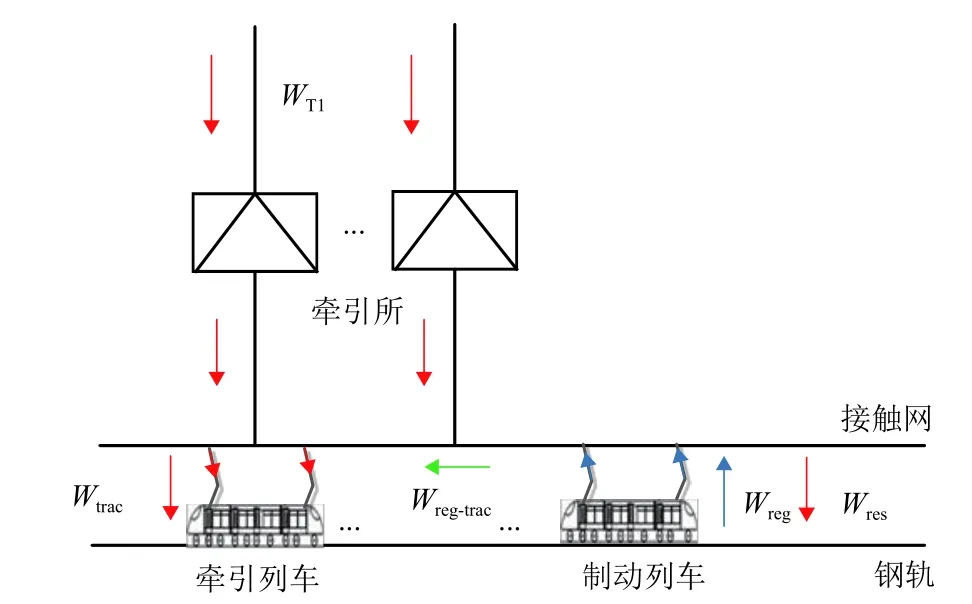
图1 参考系统能量流向示意Fig. 1 Energy flow direction of reference system
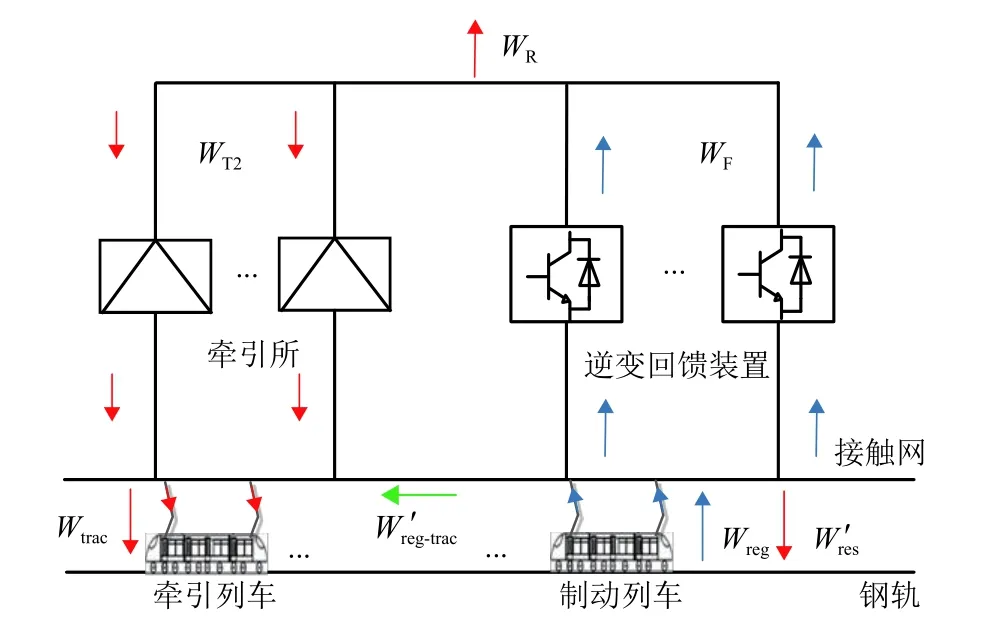
图2 安装逆变回馈装置的系统能量流向示意Fig. 2 Energy flow direction for installation of inverter feedback devices



相对于参考系统,投入逆变回馈装置后全线车载制动电阻消耗的能量变化即为列车运行所节省的总电量W,如式(4).

计及主所逆功率返送,WR未被城轨牵引供电系统利用,因此式(4)中没将WR计入总节省电量中.
定义投入逆变回馈装置后列车运行所节省的总电量与参考系统下全线牵引所输出能耗的比值为系统级节能率,选择其作为目标函数f2(X),如式(5).

综合考虑逆变回馈装置投资成本相反数以及系统级节能率,可表达为式(6)所示的城轨牵引供电系统逆变回馈装置定容选址多目标优化问题.
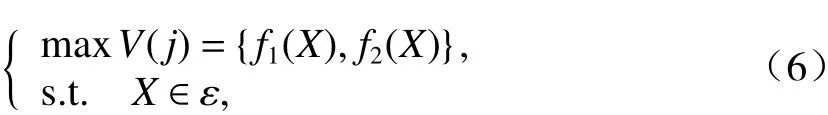
式中:V(j)为优化目标,由子目标函数f1(x)和f2(x)组成,表示逆变回馈装置容量配置Pareto 方案;j为方案数;X属于可行域ε,是以0.5 MW 为步长的随机离散变量集合[13].
1.2 约束条件
求解上述多目标函数需满足逆变回馈装置容量、逆变回馈装置启动电压、整流机组空载电压和车载制动电阻启动电压的约束条件,如式(7).
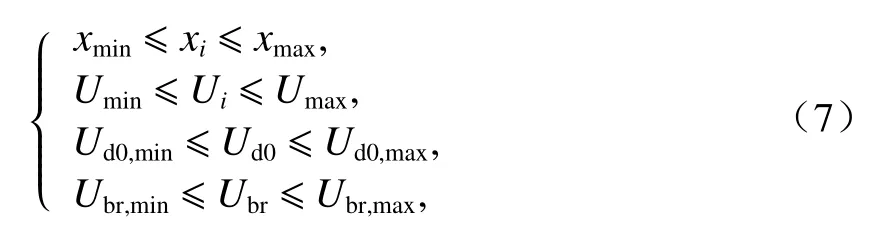
式中:第i个牵引所的Ui为逆变回馈装置启动电压;Ud0为整流机组空载电压;Ubr为车载制动电阻启动电压;xmax和xmin分别为投入逆变回馈装置容量的上、下限值;Umax和Umin分别为逆变回馈装置启动电压的上、下限值;Ud0,max和Ud0,min分别为整流机组空载电压的上、下限值;Ubr,max和Ubr,min分别为车载制动电阻启动电压的上、下限值.
2 基于NSGA-Ⅱ求解逆变回馈装置定容选址优化算法
2.1 城轨牵引供电系统交直流混合潮流算法
含逆变回馈装置的城轨交直流混合潮流计算以列车牵引计算信息和全日行车计划为计算条件,根据交直流供电系统拓扑结构建立直流侧节点电导矩阵和交流侧节点导纳矩阵,先进行直流侧潮流计算,收敛后更新牵引所运行状态,然后将直流侧电压参数收敛结果代入交流侧潮流计算,直至交流侧电压收敛. 其中,算法的可靠性以及控制策略改进分别在文献[14-15]中验证. 本文在上述算法基础上考虑了国标《城市轨道再生制动能量吸收逆变装置》(GB/T 37423—2019)规定的逆变回馈装置周期性间歇工作制[13],以120 s 为工作周期,占空比为0.25,矩形工作制如图3 所示. 图中:Ir为逆变回馈装置周期性间歇工作峰值电流.

图3 逆变回馈装置矩形工作制Fig. 3 Rectangular work cycle of inverter feedback devices
计算120 s 内逆变回馈装置吸收电流的有效值,如式(8).

式中:It为逆变回馈装置在时刻t吸收的直流电流;T为逆变回馈装置运行时间.
则120 s 内逆变回馈装置的占空比σ计算如式(9).

在交直流混合潮流算法中,根据式(9)对牵引所逆变回馈装置直流侧的电流进行限制,确保每120 s时间周期内逆变回馈装置工作占空比在0.25 以内.
2.2 NSGA-Ⅱ算法优化逆变回馈装置定容选址
NSGA-Ⅱ算法首先根据个体之间的支配关系对N组种群进行非支配排序分层,经选择、交叉和变异获得第一代子种群;然后在传统NSGA 算法基础上将父代种群与子代种群合并进行快速非支配排序,同时对每个非支配层中的个体进行拥挤距离计算,从而筛选出新的优质父代种群;最后逐次迭代直至达到迭代收敛条件或最大迭代次数,输出结果为Pareto 最优解集.
针对所提逆变回馈装置定容选址多目标优化问题,在城轨牵引供电仿真系统[16]模拟列车运行工况、牵引计算、交直流混合潮流计算,得到牵引所整流机组输出能耗、逆变回馈装置反馈能量等牵引供电系统参数,进而求解目标函数. 采用交直流混合潮流算法与NSGA-Ⅱ结合求解流程如图4 所示. 图中:g为迭代次数;VP(j)和VQ(j)分别为父代方案和子代方案.

图4 基于NSGA-Ⅱ求解逆变回馈装置容量配置优化流程Fig. 4 Optimization process of siting and sizing for inverter feedback devices based on NSGA-Ⅱ algorithm
图4 中,初始父代种群是以0.5 MW 为步长,随机产生的N组逆变回馈装置容量配置方案;G为最大迭代次数;J为交叉概率;B为变异概率;Z为整流机组额定功率;Pt和Qt分别为时刻t的父代和子代容量配置.
3 基于信息熵的TOPSIS 法最优解选取
由于上述Pareto 解集的每组解具有两个量纲属性,无法在N组Pareto 解集中挑选出一组最优解.为防止决策者偏好影响最优解选取,本文采用基于信息熵的TOPSIS 将f1(X)和f2(X)无量纲属性归一化处理,在N组Pareto 解集中筛选出与理想方案相对距离最小、与负理想方案相对距离最大的逆变回馈装置定容选址最优方案[17]. 其中,通过信息熵赋予Pareto 解集中各目标函数值的影响权重,权值大小反应了该目标函数值对最优解选取的影响程度[18].
累和归一化与向量归一化方法均不会改变目标函数的原始值属性[19],考虑本文目标函数f1(X)值为负数,因此采用累和归一化方法,如式(10).

式中:d+(j)为优化方案V(j)到理想方案归一化相对距离;d−(j)为优化方案V(j)到负理想方案归一化相对距离.
d(j)值越小则V(j)越接近理想方案.
4 算例分析
4.1 仿真模型
以广州某地铁线路一期工程进行算例仿真,该系统设有两座主变电所、10 座牵引所,线路自西向东Sub1~Sub9 共9 个车站,全长26 km,除Sub7 处为降压所外,其余车站均设有牵引所,另两座区间牵引所位置如图5,各牵引所位置信息如表1.

图5 线路供电系统结构Fig. 5 Structure of line power supply system
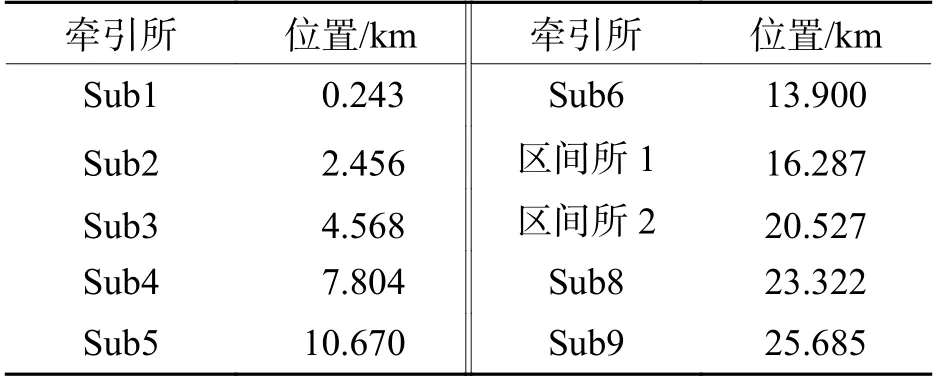
表1 牵引所位置信息Tab. 1 Traction station position information
设计考虑列车初期行车计划:运营时间段为06:30~23:30,共17 h;期间发车间隔为525 s,共发车117 对;列车车型为6B,4 动2 拖. 设置仿真参数如表2,逆变回馈装置容量与投资成本满足关系如图6 所示.

表2 仿真参数设置Tab. 2 Simulation parameter setting
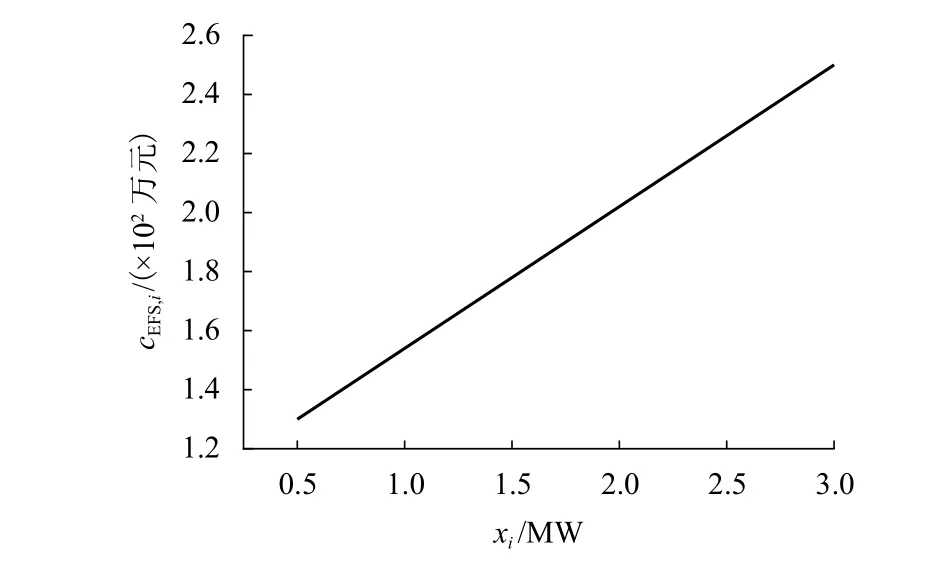
图6 逆变回馈装置价格与容量关系Fig. 6 Relationship between price and capacity of inverter feedback devices
4.2 优化过程
计算每次迭代Pareto 解集的归一化相对理想距离并筛选出各次迭代的最优方案,其目标函数值收敛过程如图7,在迭代至30 次左右时,最优方案的目标函数值基本收敛. 表3 统计了收敛后目标函数的Pareto 解集,图8(a)是Pareto 收敛解集方案的归一化相对理想距离变化情况,图8(b)在方案3~7中筛选出d(j)最小的V(7)作为该线路逆变回馈装置定容选址的最优方案. 表4 统计了V(7)的潮流计算结果,由式(5)可得系统级节能率为17.94%.

表4 最优方案V(7)每小时潮流计算结果Tab. 4 Hourly power flow calculated by optimal scheme V(7)kW•h

图7 目标函数Pareto 解集的最优方案变化过程Fig. 7 Change process of optimal scheme of Pareto solution set

图8 归一化Pareto 收敛解集Fig. 8 Normalized Pareto convergence solution set
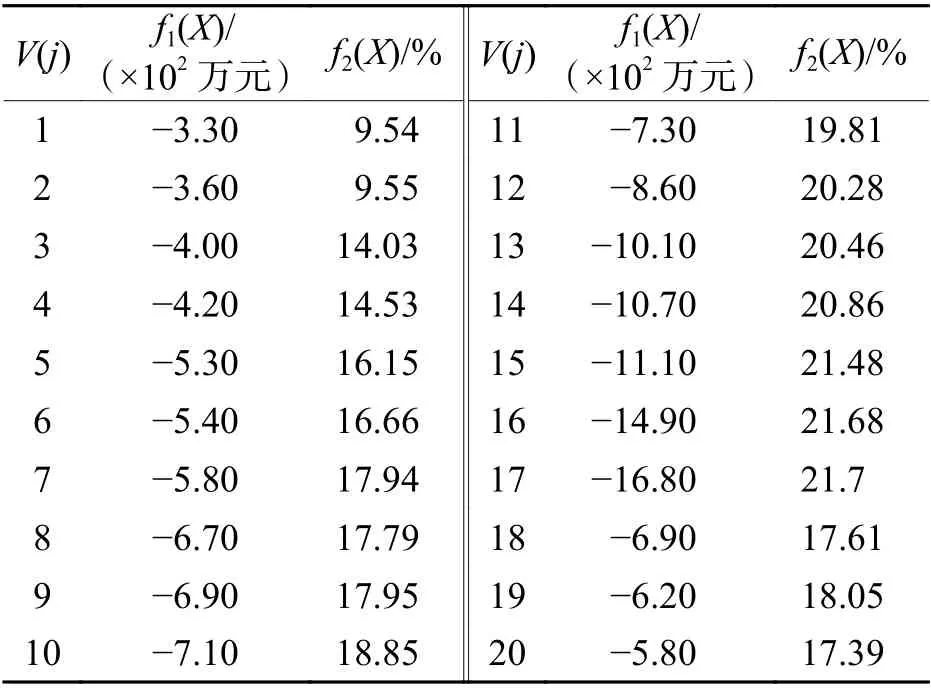
表3 Pareto 解集收敛结果Tab. 3 Convergence results of Pareto solution set
为验证该优化方案的逆变回馈装置能满足周期性间歇工作制,以区间所2 为例,统计牵引所直流电流如图9 所示. 计算525 s 发车间隔下该牵引所逆变回馈装置的工作占空比(σ),如图10 所示.

图9 区间所2 直流侧电流Fig. 9 DC current of section traction substation 2

图10 区间所2 逆变回馈装置工作占空比Fig. 10 Operating duty ratio of inverter feedback devices in section traction station 2
4.3 优化方案对比
将筛选出的最优逆变回馈装置定容选址方案V(7)与该地铁工程实际安装逆变回馈装置方案Va统计如表5,其目标函数值计算结果如表6,投资回报周期计算如式(14).

表5 逆变回馈装置方案对比Tab. 5 Scheme comparison of inverter feedback devicesMW

式中:c为投资回报周期,a;cm为地铁用电单价;D为线路全年运营天数;f1(X)单位为102万元.
从表6 可以看出:本文所提逆变回馈装置优化方案V(7)对于该地铁工程实际配置方案Va可以节省逆变回馈装置投资成本70 万元,系统级节能率提高3.25%,按0.75 元/(kW•h)电价计算,投资回报周期缩短236 d.

表6 不同优化方案目标函数值对比Tab. 6 Comparison of objective function values of different optimization schemes
由于线路牵引所Sub7~Sub8 站间距离长,列车制动频繁,优化算法搜索出在区间牵引所2 装设逆变回馈装置的方案,且线路端头所处列车制动能量相对较少,安装逆变回馈装置节能效益不高,因此建议在该地铁线路Sub2 和Sub4 处的牵引所分别安装容量为2.0 MW 和1.5 MW 的逆变回馈装置,并在区间所2 处安装容量为2.0 MW 的逆变回馈装置.
5 结 论
1) 本文将NSGA-Ⅱ与城轨交直流混合潮流算法结合对广州某地铁线路逆变回馈装置定容选址多目标优化模型进行求解,迭代30 次得到Pareto 收敛解集. 采用基于信息熵的TOPSIS 归一化目标函数值,通过比较d(j)筛选出在牵引所Sub2、Sub4 和区间所2 装设容量为2.0、1.5 MW 和2.0 MW 的逆变回馈装置优化方案.
2) 将优化方案与该地铁工程实际逆变回馈装置配置方案进行对比,逆变回馈装置投资成本节省70 万元,系统级节能率提高3.25%,投资回报周期相应缩短.
3) 该算例采用B 型列车按初期发车计划运行,发车间隔大,线路车辆稀疏,产生的制动能量较少,因此逆变回馈装置投入数量不需过多. 对于不同地铁线路,本文所述优化方法均能有效进行逆变回馈装置定容选址,提高再生制动能量利用率并缩短投资回报周期.
