基于离散单元法的铁路板结道床动力特性分析

崔旭浩 ，肖 宏 ,2

（1. 北京交通大学土木建筑工程学院，北京 100044；2. 北京交通大学轨道工程北京市重点实验室，北京 100044）

有砟轨道作为一种常用的轨道结构形式，散体道床是其重要组成部分，在长期服役过程中，不可避免会出现病害，其中道床板结是有砟轨道最主要的设备病害之一[1]. 道床板结是道砟颗粒破碎粉化产物、行车坠落及风吹降落物、路基层向上迁移的细颗粒等混合在道砟中，并在长期作用下形成的混合体.道床板结后会降低轨道弹性，加剧列车的振动冲击作用，加速轨道结构的状态恶化，缩短有砟轨道线路的服役寿命，增大线路的养护维修工作量，严重影响铁路运营经济效益，相关问题值得深入探究.

目前，国内外针对道床板结问题已开展了一定的研究工作：在试验方面，郭善辛[2]对板结道床的成因进行了分析，并对道床的脏污率、孔隙率、变形模量等参数进行了测试，提出了道床板结的参考技术指标；赵成江等[3]开展了板结道床的室内冻胀试验，研究了不同含泥量与含水量下板结道床的冻胀特性；Fortunato 等[4]开展了三轴试验指出，脏污道床的弹性模量受脏污干湿状态的影响；Tang 等[5]通过三轴试验，分析了路基土侵入有砟道床形成的脏污板结道床集料的力学特性，当脏污板结道床的含水率减小时道床的抗剪强度会提高；Paiva 等[6]进行了有砟道床的室内渗透率试验，指出随着道床中土壤含量的增加，道床的透水性迅速降低；Ishikawa 等[7]开展了不同含水率条件下洁净道床和脏污道床的室内三轴试验，结果表明，土和水的共同作用会降低有砟道床的抗剪强度. 既有的关于板结道床的试验研究多采用现场原位试验和室内三轴试验，测试分析了板结道床在水等因素作用下的冻胀、抗剪和透水性能等。但由于试验测试大多只是对宏观现象的分析，对道床内部道砟颗粒细观角度下的力学特性的揭示方面存在不足.

在理论方面，金寿延等[8]采用二自由度钢轨振动理论定性地分析道床板结对钢轨振动的影响，结果表明，道床板结会增大钢轨和轨枕的振动，降低钢轨和轨枕的位移，减弱轨道系统的弹性功能；赵宁[9]基于车轨耦合理论和有限单元法建立动力学模型，通过改变材料刚度参数模拟道床板结，其指出道床板结会增强轨道结构的振动，会使轨道结构的位移显著降低. 既有的研究手段多采用简化理论和有限单元法，多通过直接改变材料参数模拟道床板结，对于道床板结的细观力学行为的表征方面存在不足，并且也无法有效地考虑有砟道床的散粒体特性.

综上，既有针对道床板结的研究大多没有从细观角度出发分析板结对有砟道床力学特性的影响，并且在考虑有砟道床的散体特性方面存在不足. 有砟道床由不同粒径的道砟颗粒堆积而成，具有散体特性. 板结道床是由于道砟颗粒之间的脏污材质相互胶结作用而形成的硬块，具有一定的整体性，但是在列车荷载作用下道砟颗粒之间的胶结作用可能被破坏，或者板结程度较低时道砟颗粒之间并没有完全粘接牢固，导致板结道床处于介于散粒体和连续体之间的状态，用有限单元法模拟散体道砟存在一定的不足，未有效考虑道砟颗粒及脏污板结材质的散体特性. 基于此，本文将采用离散单元法建立脏污道床的仿真分析模型分析列车荷载作用下道床板结对有砟道床动力行为的影响，并从细观角度揭示板结使道床弹性降低的内在原因，相关结论可为有砟道床的养护维修提供参考.

1 模型建立

大规模离散元数值模拟对计算设备具有极高的要求，直接建立三维模型开展分析会消耗大量的计算资源. 考虑到实际中有砟道床主要承受列车垂向荷载的作用，可主要关注道砟颗粒沿竖向的运动情况，为此，可将铁路线路简化为二维问题进行数值模拟[10]. Zhang 等[11]验证了有砟道床的二维离散元模型适用于有砟道床的动力特性分析. 另外，板结道床中的细小脏污颗粒数量巨大，会极大地增加仿真计算量，所以经比选后采用二维离散元模型进行仿真分析.

道砟颗粒形状对颗粒力学行为有重要影响[12]，实现对道砟颗粒真实外形的模拟是仿真计算的关键所在. 本文首先利用数码相机对道砟颗粒进行图像采集，然后运用图像处理技术获得道砟颗粒的外轮廓信息. 并根据道砟颗粒的轮廓信息，基于离散元软件PFC 用clump 单元模拟道砟颗粒，如图1 所示.

图1 道砟颗粒建模Fig. 1 Ballast particle modeling

按照《铁路碎石道砟》（TB/T 2140—2018）[13]中特级碎石道砟要求生成散体道床模型. 首先通过Fish 语言编程，设置每个粒径区间道砟质量的上下限，结合clump distribute 命令和bin 关键词控制道砟的级配，通过落雨法并配合分层压实最终得到密实的道床. 另外，参考已有文献[11,14]，钢轨和扣件采用ball 单元模拟，在单元之间建立平行黏结接触模型，实现对钢轨的连续性模拟. 轨枕则采用clump 单元模拟，轨枕及道砟颗粒之间采用线性接触模型.

线性接触模型的计算式[15]为

建立有砟轨道离散元模型如图2 所示. 将轨枕从左至右依次进行编号. 所建模型中道砟颗粒的clump 数量为1 227 个，内部共含151791 个pebble单元. 模型全长为50.4 m，对中间的9 跨轨枕建立完整的道床模型，为减小计算量，对其余区域进行简化仅建立钢轨和扣件模型，约束模型两端钢轨沿水平方向的位移.

图2 有砟轨道离散元整体模型（单位：m）Fig. 2 Discrete element model of ballast bed (unit：m)

板结道床是由于道砟的粉化、脏污与道砟间胶合物质的相互作用使道砟粘接成块而形成的. 从板结道床的微观结构出发，可将板结道床视为混有粘胶、具有一定黏结力的道砟体[16]. 本文将道砟颗粒视为块体单元，在洁净道床模型中道砟颗粒的空隙之间投放小颗粒单元模拟脏污介质，通过定义脏污颗粒之间的黏结作用模拟道床板结现象. 道砟颗粒之间采用线性接触模型进行模拟.

采用直径2 mm 的圆盘单元模拟脏污颗粒. 板结程度近似采用文献[17]中的脏污指标进行评估，即认为对于脏污较严重的道床，在定义脏污颗粒之间的黏结作用后用于模拟板结较程度较严重的道床. 所建立的板结道床的局部模型如图3 所示.

图3 板结道床局部模型Fig. 3 Local model of hardening ballast bed

通过控制板结道床中脏污颗粒数量的多少，共设置4 种计算工况，以分析道床板结以及道床板结程度对有砟道床动力特性的影响，如表1所示.

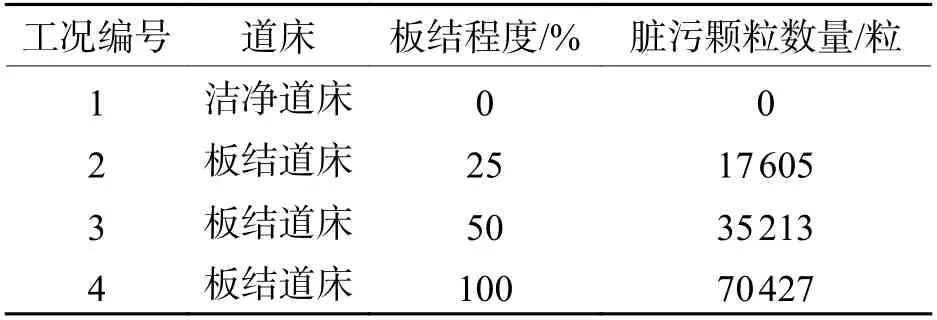
表1 计算工况Tab. 1 Calculation conditions

参考文献[16]，离散元模型的计算参数如表2所示，忽略脏污颗粒的材质影响，取脏污颗粒的刚度参数与道砟颗粒一致.

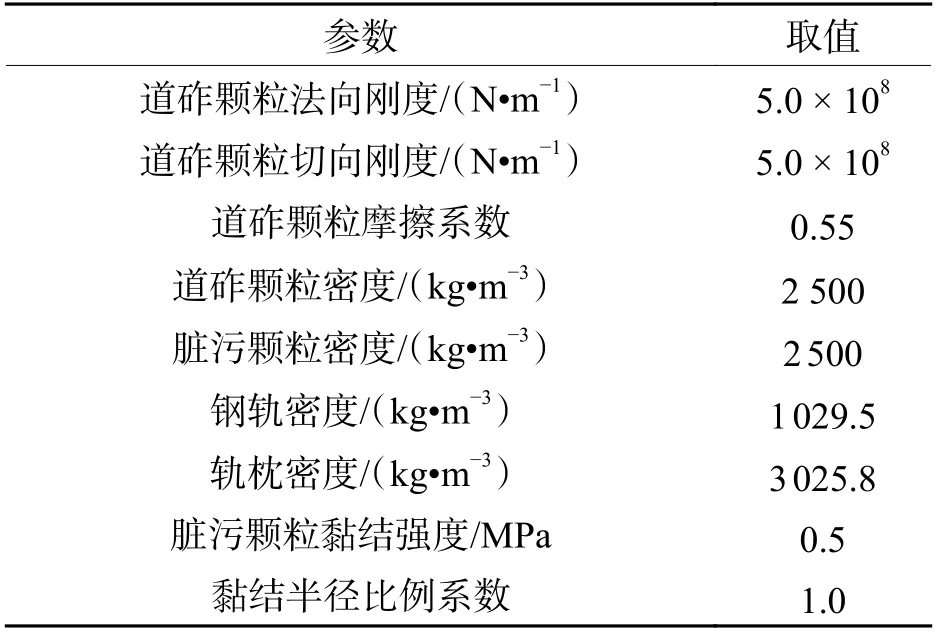
表2 离散元模型计算参数Tab. 2 Parameters of DE model

2 模型验证

开展现场动测试验以校验模型，选定某有砟道床试验段开展动态测试. 根据《轨道检测道床应变、振动测试方法》（TB/T 2488—2017）[18]，现场测试中道床加速度传感器的埋设位置位于枕底以下15 cm位置处，测试过程中列车的运行速度为40 km/h. 在离散元模型中通过在钢轨上施加经过平面应变变换的移动荷载模拟列车作用，并对枕底以下15 cm 处的道砟颗粒的加速度进行记录. 道床加速度实测结果、仿真结果以及频谱变换如图4 所示.

图4 道床振动加速度Fig. 4 Ballast bed vibration acceleration

由图4 可以看出：现场实测的道床加速度与离散元模型仿真得到的时程曲线的幅值及波形相近.因现场线路存在不平顺，导致实测结果存在明显的毛刺现象，但现场实测的道床振动加速度的频谱曲线与离散元计算的道床振动加速度的频谱曲线波形及幅值相近，振动的主频成分也相吻合. 其他不同速度的列车荷载下道床加速度测试和计算结果相对比后均能得到同样的验证结果. 从而验证了本文所建立模型的正确性.

3 计算结果分析

在钢轨上施加移动的轴重荷载进行动力仿真.考虑到道床的振动和受力是导致道砟粉化破碎的最主要因素[19]，本文将对列车荷载作用下道砟颗粒的振动加速度、接触力进行监测. 另外，还将分析列车荷载作用下道砟颗粒之间的相对滑动情况，以期揭示板结道床弹性降低、刚度增大的细观机理.

3.1 道砟颗粒振动

在仿真过程中对道砟颗粒的振动加速度进行监测. 限于篇幅，仅给出工况1 中当列车的第二个轮载位于 ⑤ 号轨枕上方时道砟颗粒振动加速度的整体矢量图以及中间 ④ 号、⑤ 号和 ⑥ 号轨枕的局部矢量图，如图5 所示. 图中：P为列车荷载；v为列车速度.

由图5 可看出：在列车荷载作用下，道砟颗粒的振动加速度矢量分布较为混乱，同一时刻不同位置处道砟颗粒的瞬时加速度存在显著差异，这是道床散体特征的表现. 道砟颗粒的振动加速度受道砟颗粒自身重量、形状以及与周围道砟颗粒的接触状态等诸多因素影响. 分析发现其他计算工况也存在类似的规律，这也反映出即便是板结道床，也具有明显的散体特性. 板结会使得道床的力学特性更趋向于连续介质的表现，但在列车荷载作用下，道砟颗粒之间的板结介质并未将道砟颗粒黏结成一个牢固的整体，板结道床的问题仍然可以划定为散体力学范畴.

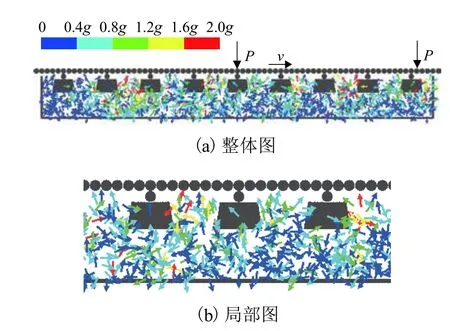
图5 道砟颗粒振动加速度矢量图Fig. 5 Vector diagram of ballast particle vibration acceleration

进一步量化加载过程中道砟颗粒的振动情况，选定各轨枕正下方15 cm 附近的道砟颗粒进行分析. 考虑到粒径较大的道砟颗粒的配位数更多，其振动状态更为稳定，故所选取道砟颗粒的粒径大于4.5 cm. 对选定的道砟颗粒振动加速度进行监测. 限于图幅，给出工况1、2 中 ⑤ 号轨枕下方道砟颗粒的振动加速度时程结果，如图6 所示.

图6 5 号轨枕下方道砟颗粒振动加速度时程曲线Fig. 6 Time history curves of ballast particle vibration acceleration under No. 5 sleeper

由图6 可以看出：工况1 和工况2 中的 ⑤ 号轨枕下方道砟颗粒的振动波形较为相似，均是在转向架荷载经过时道砟颗粒的振动加速度增大并出现最大值；工况1 中 ⑤ 号轨枕下方道砟颗粒的振动加速度幅值为1.89g，工况2 中 ⑤ 号轨枕下方道砟颗粒的振动加速度幅值为2.08g.

各工况中不同轨枕下方所选定道砟颗粒的振动加速度幅值，结果如图7 所示.

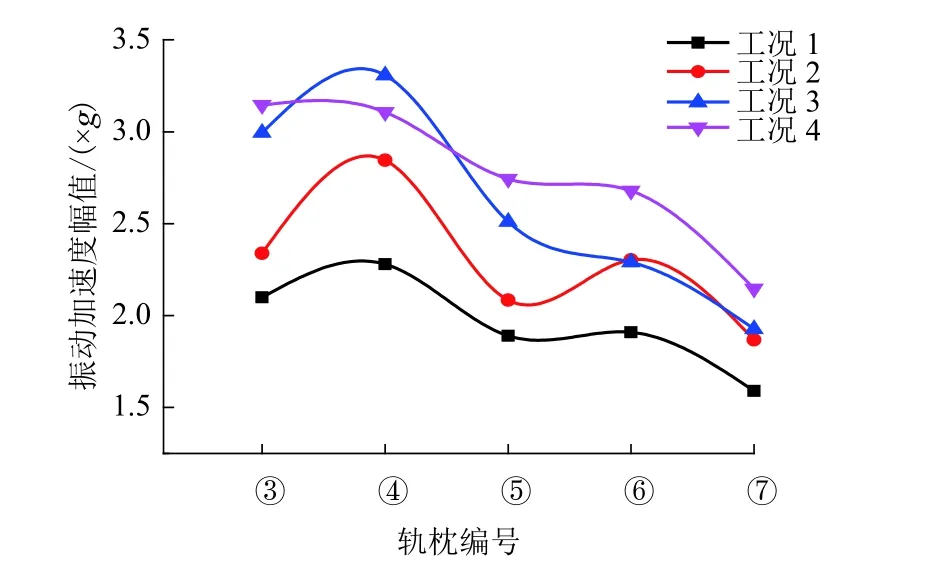
图7 道砟颗粒振动加速度幅值Fig. 7 Peak vibration acceleration of ballast particles

由图7 可知：同一工况中不同道砟颗粒的振动加速度幅值有所不同，这是由于有砟道床的散体特性导致，道砟颗粒受其自身重量、外形及与周围道砟颗粒的接触状态等因素的影响；工况2～4 中道砟颗粒振动加速度的幅值均大于工况1，且有依次增大的趋势；对4 种计算工况中各自道砟颗粒振动加速度幅值取平均，工况1～4 依次为1.94g、2.30g、2.54g和2.69g，工况2～4 比工况1 分别增大了18.56%、30.93%和38.66%. 因此可知，道床板结会增大道床中道砟颗粒的振动水平，且影响程度随着道床板结程度的增大而增大.

为使结果更具代表性，选取不同工况中 ⑤ 号轨枕下方15 cm～20 cm 区域的多个道砟颗粒，统计其各自的加速度，结果表明不同道砟颗粒之间的振动存在差异，但对不同道砟颗粒的振动加速度峰值取平均后，经对比发现道砟颗粒振动仍然存在随着板结程度增大而增大的趋势.

3.2 道砟接触力

为量化道床板结对道砟颗粒接触力的影响，对列车荷载作用下各轨枕下方道砟颗粒之间的接触力进行监测，在仿真过程中对每根轨枕中心位置两侧各0.3 m 范围内的道砟颗粒接触力进行遍历并取平均，得到每根轨枕所在区域处的道砟颗粒平均接触力. 限于篇幅，仅给出4 种计算工况的 ⑤ 号轨枕处道砟颗粒之间的平均接触力时程曲线，如图8 所示.

由图8 可看出：各工况中道砟颗粒平均接触力的时程曲线较为相似，均是在列车轮载经过时逐渐增大；4 种计算工况中道砟颗粒平均接触力的峰值有所不同，工况1～4 的道砟颗粒平均接触力的峰值依次为1.21、1.23、1.28 和1.38 kN，工况2～4 比工况1 分别增大了1.65%、5.79%和14.05%. 由此表明，板结因弹性减低而导致列车荷载对道床的冲击作用加强，从而增大道砟颗粒的接触受力.

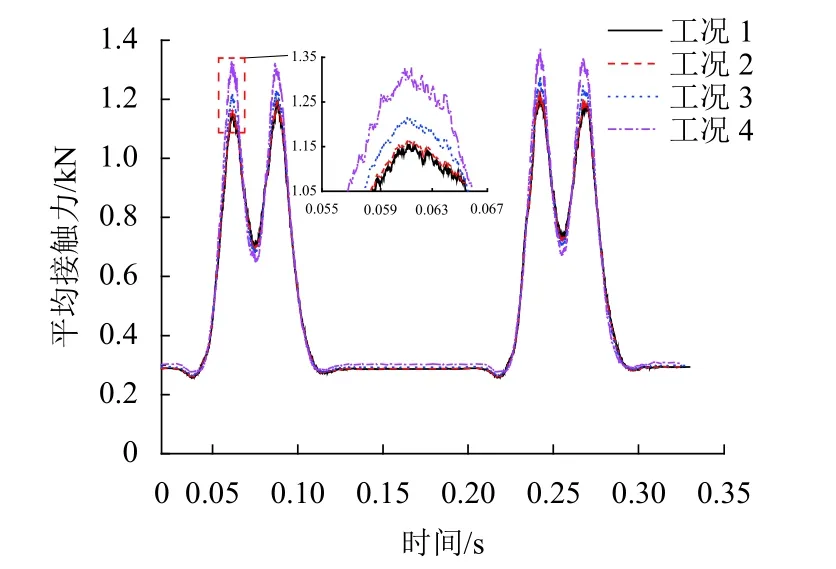
图8 道砟颗粒接触力均值时程曲线Fig. 8 Time history curves of mean contact force of ballast particles

4 种计算工况的各道砟箱中道砟颗粒平均接触力的幅值如图9 所示.

图9 道砟颗粒平均接触力峰值Fig. 9 Peak of average contact force of ballast particles

由图9 可知：同一工况的不同轨枕下方道砟颗粒平均接触力的幅值有所不同，且道床板结会放大此差异；工况1 中的 ③ 号轨枕下方道砟颗粒的受力较 ④ 号轨枕下方的道砟颗粒的受力大7.34%，而工况4 中差异增大到了12.47%. 由于有砟道床是散粒体材料，不同轨枕位置处道床的密实程度不尽相同，导致道砟颗粒的受力略有差异. 由此表明，板结会增大道床中不同区域处道床服役状态的差异性，增加了道床刚度的不均匀性.

3.3 道砟颗粒相对滑动

板结道床在宏观方面的表现是使道床弹性丧失，引起轨道刚度急剧增加. 为从细观角度揭示板结道床引起道床刚度增大的机理，本文记录仿真计算过程中道砟颗粒的相对滑动情况. 定义道砟颗粒之间发生滑动的接触数量与总接触数量的比值为滑动分数. 图10 为仿真过程中工况1 和工况4 的 ④ 号轨枕下方道砟颗粒的滑动分数时程曲线.

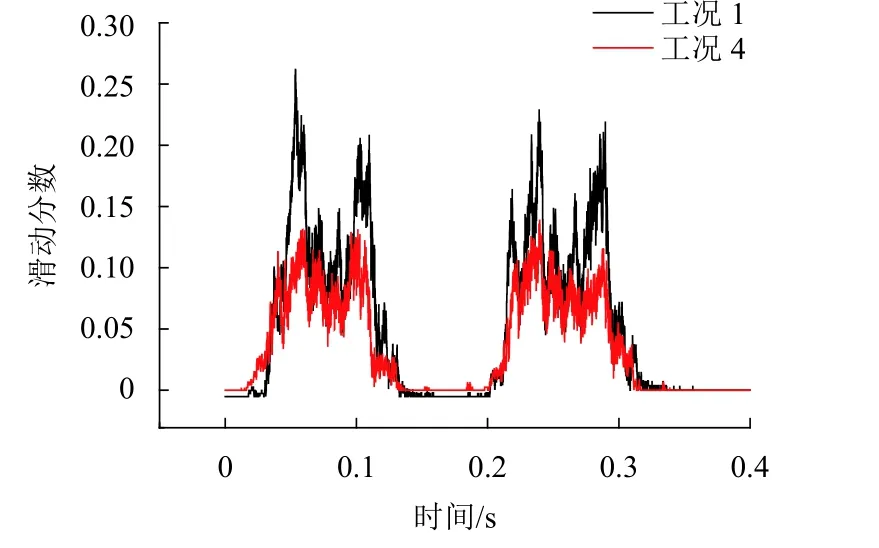
图10 道砟颗粒滑动分数Fig. 10 Slip fraction of ballast particles

由图10 可知：工况1 和工况4 中道砟颗粒滑动分数的时程波形较为相似，均是在列车经过时逐渐增长；工况1 中道砟颗粒滑动分数的幅值为0.263，工况4 中道砟颗粒滑动分数的幅值为0.122，工况4的比工况1 的减少了53.61%. 因而可知，板结会降低列车荷载作用下道砟颗粒之间接触发生相对滑动的几率，使更多的接触由发生滑动的活跃状态转化为不发生滑动的稳定状态. 另外还可看出，虽然工况4 板结道床中道砟颗粒的滑动分数相比工况1 的洁净道床有所减低，但并不为0，这也表明在列车荷载作用下板结道床内部道砟颗粒之间仍然存在滑动现象，板结道床仍具有散粒体的特征.

图11 为列车荷载作用于 ⑤ 号轨枕上方时道砟颗粒之间所有接触在每一时步中的切向滑动位移量. 由于本文所建模型中含有大量粒径较小的脏污颗粒，故设定了较小的计算时步，从而导致道砟颗粒在单一时步中的滑动位移量值较小.

由图11 可知：工况1 中道砟颗粒在单一时步中瞬时滑动位移的最大值为21.12 nm，工况4 的瞬时滑动位置的最大值为7.23 nm，比工况一的降低了65.77%. 可以看出，板结降低了道砟颗粒之间滑动位移的量值.

图11 单一时步中道砟颗粒切向滑动位移Fig. 11 Sliding displacement of ballast particles in a single time step

板结减小道砟之间滑动程度的原因是由于板结介质改变了道砟颗粒之间的接触状态，如图12 所示. 为便于表述，将图中所示的道砟颗粒分别编号为1 号道砟和2 号道砟. 由图12 可知：脏污板结填充了道砟颗粒之间的空隙，由于有砟道床为散粒体，外部荷载作用下相邻道砟颗粒之间速度方向不尽相同，可能存在相向运动的速度分量，例如图12 中的1 号和2 号道砟颗粒. 在洁净的道床中，1 号和2 号道砟颗粒不存在直接相互作用，而是通过彼此相邻的道砟传力，容易引起与相邻道砟之间产生滑动位移；而脏污道床中1 号和2 号道砟颗粒之间的脏污板结形成了新的传力路径，起到了分担荷载的作用，从而减低了这两颗道砟与周围道砟之间的接触力，导致道砟之间不再滑动或降低滑动位移.

图12 道砟颗粒运动示意Fig. 12 Schematic diagram of the ballast particles movements

有砟道床在列车荷载作用下道床中道砟颗粒之间会出现相对滑动和错位，消耗了列车荷载传递至道床的能量，并在宏观上表现出道床整体的弹塑性变形，保证了有砟轨道的弹性充足. 而板结道床中的脏污板结材质降低了道砟之间发生相对滑动的几率，同时还会降低滑动程度（相对滑动位移）. 这反映出板结抑制了道床中细观角度下相互咬合的道砟颗粒之间的相对运动，导致有砟道床的力学特性更趋向于连续介质材料，使得道床在宏观上表现得更不易被压缩，从而削弱了有砟道床的弹性机能，导致道床刚度增大. 因此对于道床板结严重的地段应及时进行清筛养护作业，以避免因道床刚度过大而引发其他次生病害.

4 结 论

本文建立了板结道床的离散元分析模型，分析了列车荷载作用下道砟颗粒的振动、受力及颗粒滑动等宏细观力学特性，结果显示：

1） 列车荷载作用下，板结道床中不同道砟颗粒的振动状态存在显著差异，且道砟颗粒之间存在相对滑动现象，说明板结道床仍具有散体特性. 道床板结会提高道砟颗粒的振动水平，并且道床板结越严重对道砟颗粒振动水平的影响越大.

2） 道床板结会增加增大列车荷载对道床的冲击作用，从而增大道砟颗粒的接触受力，增加了道砟颗粒发生破碎劣化的风险；由于脏污颗粒在道床中的位置分布较为随机，导致不同区域处道砟颗粒受力状态的差异性变大，增加了道床刚度的不均匀性.

3） 脏污板结材质会减小道砟颗粒之间发生相对滑动的几率，同时会减小道砟颗粒之间的滑动量值，脏污板结在细观角度下对道砟颗粒相对移动的抑制是引起宏观上的道床弹性丧失、刚度变大的重要原因.