介质黏度对旋流泵内流结构的影响
2021-12-28权辉于欣洋李雅楠宋凯浦海燕王卫华
权辉,于欣洋,李雅楠,宋凯,浦海燕,王卫华
(1. 兰州理工大学能源与动力工程学院,甘肃 兰州730050; 2. 江苏双达泵业股份有限公司,江苏 靖江 225300)
随着工农业的不断发展,泵输送多种复杂介质和含有杂质的流体的应用规模日益扩大,旋流泵作为一种无堵塞泵应用愈加广泛[1-2].
在输送的介质上,旋流泵主要集中于固液两相流、盐析两相流与清水等介质,在黏度对旋流泵内流场的影响方面研究较少.李文广等[3]对旋流泵在不同黏度下的性能进行了对比,液体黏度对流量和效率修正系数的影响较小,对扬程的修正系数影响较大.在化工方面,已有大耐泵业生产输送丁基橡胶的旋流泵.
在最初的流动模型中,学者们将旋流泵内划分成不同的区域,从而解释旋流泵内复杂的流动结构,并对旋流泵在两相流与清水的内部流动机理、水力性能、能量转换等方面做了大量的研究[4].权辉等[5-7]对旋流泵内流结构提出了次流涡的概念,并对旋流泵在固液两相流情况下对循环流涡结构提出了新的湍流模型,进一步解释了旋流泵的内流结构.旋流泵由于其优异的无堵塞性而被广泛应用,在化工废液的输送过程中,黏度是影响性能的主要因素,但目前缺乏黏性对旋流泵内流动特性的影响的研究.因此文中对不同黏度的介质如何提高性能与解决内流结构之间的关联进行研究,可为旋流泵在化工领域应用提供理论参考.
1 模型建立与数值方法
1.1 模型建立及网格划分
以150WX-200-20型卧式旋流泵为研究对象,其各项设计参数分别为流量Q=200 m3/h、扬程H=20 m、额定转速n=1 450 r/min、轴功率P=26.34 kW.旋流泵的水力几何参数如表1所示,由此得到其水力设计如图1所示.利用Creo软件对该旋流泵计算域进行三维建模.

图1 旋流泵水力设计图

表1 旋流泵水力几何参数
采用ICEM结构化网格划分,将流体域分为进口段、叶轮域和蜗壳域3个部分,采用Interface面耦合,对边界层进行网格加密.边界层网格层数为15层,壁面附近第一层网格厚度为0.01 mm,壁面y+<15满足要求,如图2所示.

图2 计算域网格示意图
为了检验网格无关性,对6套网格在清水额定工况下进行数值模拟,得到了与网格数n对应的扬程,如图3所示.当网格数为157万,扬程的变化不超过1%,且加密网格数对数值计算结果的影响较小,因此以该网格模型进行数值分析.
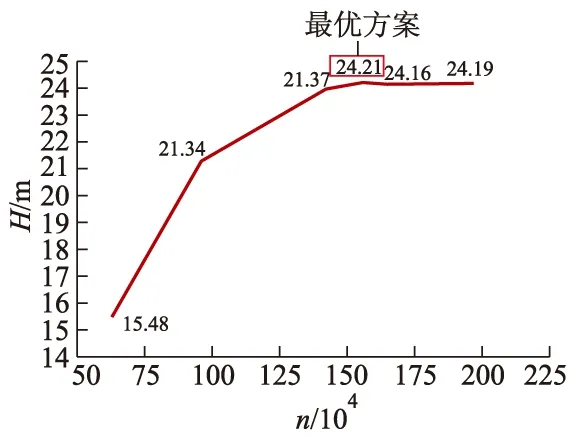
图3 网格无关性检查
1.2 旋流泵内流场的数值计算
文中选用的混合物密度为1.35×103kg/m3.对于化工废液可看成不可压缩流体,采用定常计算.由设计可知,叶轮转速为1 450 r/min,进口条件设置为速度进口,出口流动设置为自由出流.为了保证计算精度,同时节约计算时间,采用SIMPLEC算法,二阶迎风的离散格式,残差精度为10-6,使用RNGk-ε湍流模型,SIMPLEC算法,考虑重力作用,当残差曲线达到精度和出口压力稳定时即流场计算结果视为收敛.蜗壳设为静止无滑移壁面条件,叶轮设为运动无滑移壁面条件[8].
2 数值方法验证与流动结构表征
2.1 试验测试台系统
为验证数值计算结果可靠性和准确度,建立旋流泵开式试验测试系统,以清水为介质对同一模型进行试验测试和数值模拟,如图4所示.

图4 试验装置示意图
图5为试验测试与数值模拟得到的性能曲线.分析可知,测试和数值计算所得扬程和效率的平均误差分别为2.27%和5.26%,误差均小于6.00%,从而间接验证了模型及数值方法选择具有较高可靠性.

图5 水力性能误差验证
2.2 截面选取方案
旋流泵内存在循环流、贯通流和大量自由涡,为了研究旋流泵内流动特性,对旋流泵建立直角坐标系及极坐标系,并按如图6所示的方案选取截面来描述流动特性.

图6 截面选取方案图
2.3 循环流与贯通流的几何特征
旋流泵内流动结构主要以循环流和贯通流为主,除此之外还存在大量次生涡.根据流道内流体的运动情况,每个轴截面上一般存在3个尺度较大的涡,如图7所示.主循环流C1主要在无叶腔中的Ⅱ区域,在不同的流动情况下,会有一部分在叶轮域与后缩腔内.为了方便描述,将无叶腔分为3个部分,Ⅰ区流体受进口段影响被吸入叶轮域,Ⅱ区为循环流主要所在区域,Ⅲ区为贯通流主要所在区域.

图7 无叶腔内区域分区
为了进一步研究旋流泵内流结构,根据流线形状定义循环流与贯通流的边界.在流线图内识别出一根流线,其包裹循环流或贯通流涡核且外侧流线不闭合或不能完整包含循环流或贯通流,则视为循环流或贯通流边界.
2.4 循环流与贯通流的压力梯度表征
为定量描述旋流泵内涡结构,引入压力梯度∇p和速度梯度∇v.将旋流泵内循环流涡带在截面上的边界与压力梯度图重合,如图8所示.
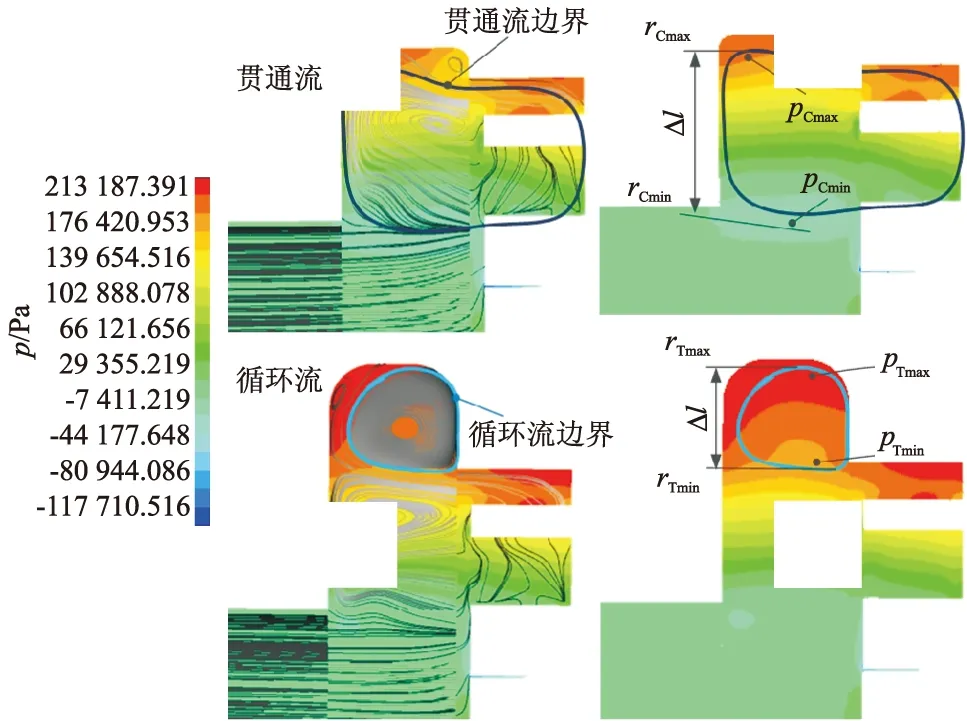
图8 压力梯度表征图
在径向截面上定义循环流压力梯度为
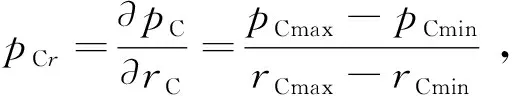
(1)
式中:∇pCr为循环流边界上rmax处与rmin处压力差,从压力梯度云图上可知,压力大小与半径大小呈正相关,故可以确定rmax处压力为最大值即pmax,同理可知rmin处为压力最小值pmin.
同理定义贯通流压力梯度∇pTr为
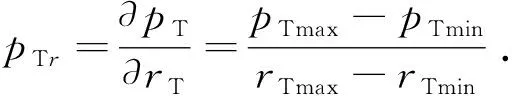
(2)
3 黏度对旋流泵内流结构的影响
3.1 不同黏度下旋流泵外特性变化
流体微团之间的黏性力会随着黏度的增大而增大,进而影响泵内流体能量的传递.图9为旋流泵在输运不同黏度的化工废液时的外特性曲线.
由图9可知,在黏度μ为0.10 Pa·s左右旋流泵外特性变化明显.当黏度为0.01 Pa·s时,扬程曲线下降缓慢,轴功率最低,扬程最高,效率最佳点位于1.2Q附近.随着黏度继续增大,当黏度大于0.10 Pa·s后,最佳效率点向前移动,扬程下降,轴功率增加.当黏度增大至1.00 Pa·s后,0.8Q时为最佳效率点,轴功率进一步增加,扬程进一步降低.这是因为随着黏度增大,流体一部分是因黏度提升使得流体微团间的剪切力提高,同时,另一部分边界层变厚,在近壁面处的速度梯度变小,在扩散管处液体黏度大,使得低速流体在扩散管内受到挤压,从而导致其效率降低,扬程下降,轴功率增加.

图9 不同黏度外特性曲线图
3.2 输送化工废液时旋流泵内流结构变化
3.2.1 叶轮域内流结构变化
对于叶轮域,其截面l1,l2,l3流线如图10所示,其中v为速度矢量.
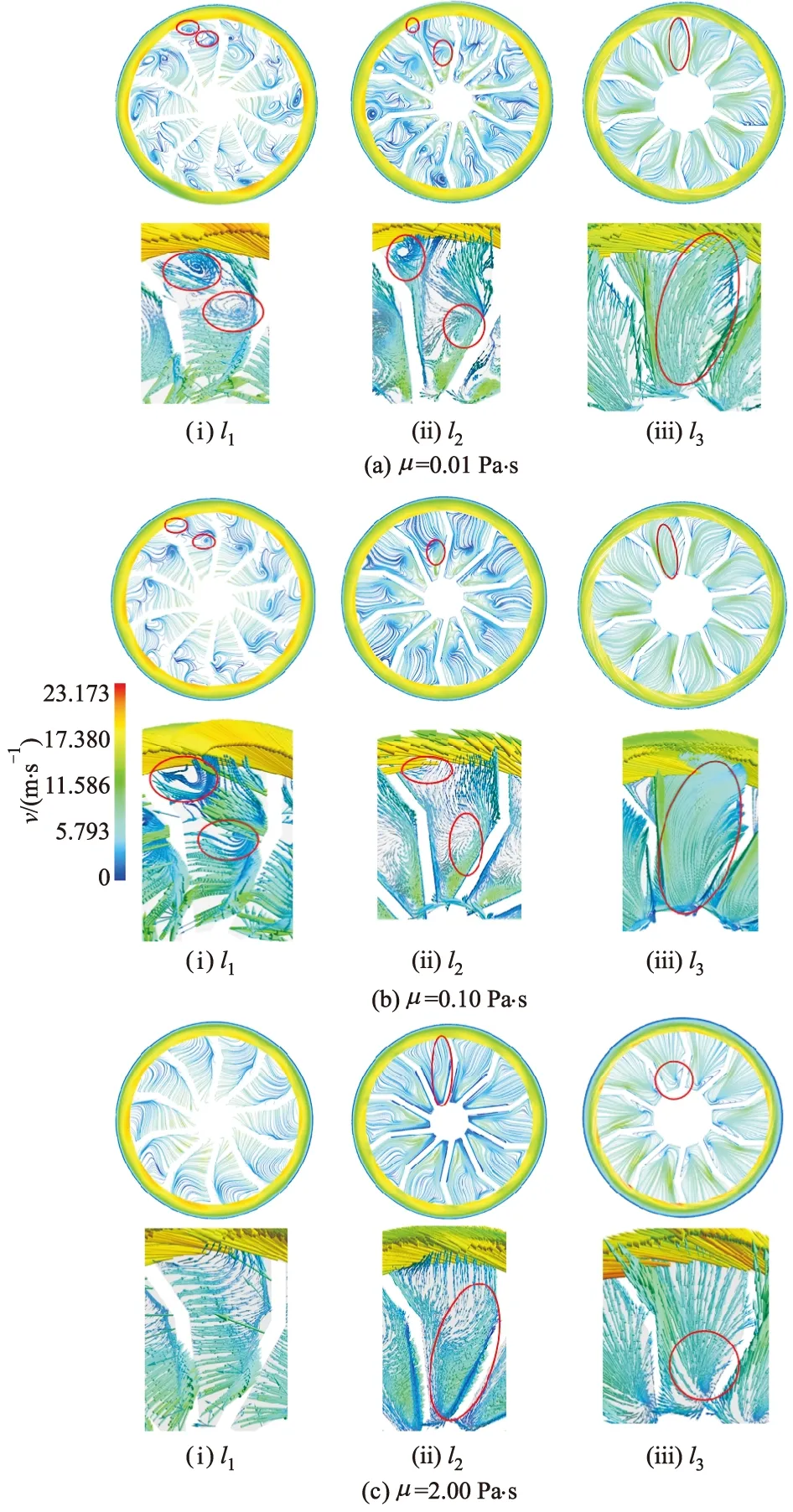
图10 3种介质下叶轮域流线图与速度矢量图
分析图10可知,黏度0.01 Pa·s时在叶轮轮毂处流动简单,叶轮吸入的液体尚未受到循环流与叶轮做功的影响,涡旋较少.而在叶轮轮缘附近流场涡旋较多,在截面l3存在循环流.当黏度为0.10 Pa·s时,叶片折点处的涡旋减少,在截面l2循环流消失.当黏度为2.00 Pa·s时,叶轮折点无涡旋且在截面l1上流线为圆周方向的弧线,叶轮域内几乎没有循环流.流体在叶轮的作用下向后缩腔运动,堆积在叶轮轮缘处.相比于较低黏度的流体,流体的挤压使效率降低,同时造成了一部分能量的损失.
3.2.2 不同黏度下的内流结构
选取黏度为0.01,0.10,2.00 Pa·s的介质,模拟在流量分别为0.4Q,1.0Q和1.4Q时截面A2与A8流线,得到2.3节中定义的循环流与贯通流边界,如图11所示,图中蓝色曲线为截面A2上,红色曲线为截面A8上.
由图11可知,随着黏度增大,截面A2与A8上循环流形状差异也随之增大,结合图9,效率的变化也随之增大.当黏度为0.01 Pa·s时,此时截面A2与A8上的循环流形状在轴向与径向上的距离变化不大.当黏度增大至0.10 Pa·s时,循环流被挤压在无叶腔内,此时效率开始下降.黏度增大至2.00 Pa·s,循环流在小流量处截面A8上大于截面A2上,而随着流量增大,截面A8上循环流逐渐缩小,直至成为一个细长的椭圆状.这是因为循环流和次流涡随着黏度增大而增大,挤占贯通流的空间,使得旋流泵的效率降低.
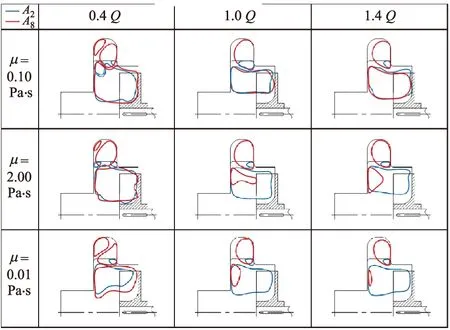
图11 循环流与贯通流边界图
3.3 介质黏度对压力梯度的影响
对黏度为0.01,0.10,2.00 Pa·s的内流进行数值模拟,得到贯通流与循环流压力梯度变化分别如图12,13所示.

图12 贯通流压力梯度变化
由图12可知,贯通流压力梯度∇pTr随流量和黏度的增大而增大.结合效率曲线可以看出,当黏度在不大于0.10 Pa·s时,在最佳效率点处时压力梯度差∇pTrmax-∇pTrmin最大,压力梯度在最低值与最高值分别为500 kPa/m和3 000 kPa/m.当黏度大于0.10 Pa·s时,当超过最佳效率点后,压力梯度急剧增加.在最佳效率点处压力梯度最高值与最低值之差为0~500 kPa/m.随着黏度的增大,旋流泵在蜗室Ⅲ处压力降低,贯通流压力梯度降低.
分析图13可知,当黏度为0.01~0.10 Pa·s时,循环流占据了蜗室Ⅱ的大部分空间.随着流量的增大,循环流的压力梯度先减小后增大,当黏度在0.10~2.00 Pa·s时,随着流量与黏度增大,循环流压力梯度下降,当到达最佳效率点时反而增大.在最佳效率点,循环流内没有次流涡,此时占据了蜗室Ⅱ的位置,黏度在0.01~0.10 Pa·s时,因黏度低而使得循环流变形小,由此压力梯度大同时效率高.当黏度大于0.10 Pa·s时,循环流在截面A5—A8轴向缩小至无叶腔靠近进口段的一侧,同时在径向也缩小,压力梯度变小,效率最高.
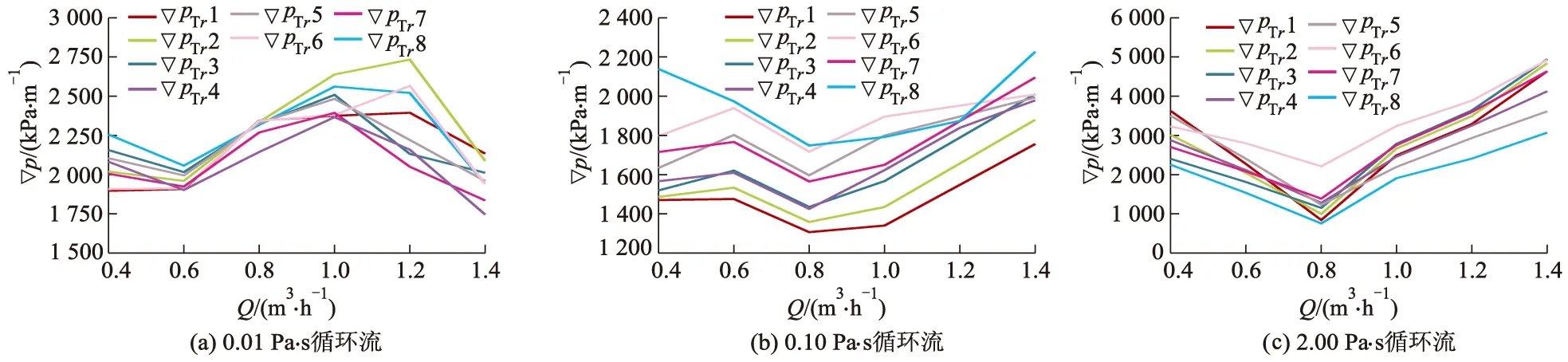
图13 循环流压力梯度变化
在对旋流泵内流结构有了一定的了解后,应该对旋流泵输送清水和化工酸液时两相流的内流特性进行对比,并结合旋流泵的过流部件进行设计,在进一步提升旋流泵的水力效率的同时保持旋流泵良好的无堵塞性.
4 结 论
1) 旋流泵内流结构受黏度影响较大.黏度2.00 Pa·s与黏度为0.01 Pa·s内流结构差异大,黏度2.00 Pa·s相比黏度为0.01 Pa·s时,循环流被挤压后,使叶轮域流体被堆积在后缩腔,反而降低了旋流泵的效率.
2) 黏度对旋流泵内循环流与贯通流的边界形状有较大影响.随着黏度的增大,自由涡减少,循环流逐渐被挤压,远离叶轮域至无叶腔的另一端.而小流量会减小循环流变形,所以最佳效率点会向小流量方向移动.
3) 在最佳效率点处,不同截面上贯通流压力梯度变化相对均匀,递减越均匀,效率越高.当黏度在0.01 ~0.10 Pa·s时,最佳效率点处最大压力梯度与最小压力梯度差最大则效率高.当黏度大于0.10 Pa·s时,循环流压力梯度差值最小时效率最高.
