层状红壤水分入渗特征试验与模拟

涂安国，聂小飞，李英，李洪任*

(1. 江西省土壤侵蚀与防治重点实验室，江西 南昌 330029； 2. 江西省水土保持科学研究院，江西 南昌 330029； 3. 中国科学院教育部水土保持与生态环境研究中心，陕西 杨凌 712100)

异质的土壤架构如何控制水文过程是水文土壤学研究的热点问题之一[1].由于自然成土过程和人为耕作作用，自然界中土壤大都呈现为交错分布的层状结构，形成复杂多变的土壤剖面结构.层状土内产生了微观损伤与宏观断裂面，因而水力特性不同于单层均质土壤.试验研究表明，不同质地层状土壤水分运动明显不同于均质土壤，主要表现为层状土壤分层界面处存在毛管障碍，降低了土壤水分下渗速率[2-3].层状土壤质地的不均匀性使得土水势在界面处发生突变[4]，因而入渗水分在界面处的运动方式也发生相应的变化.层状界面对土壤水分运动的影响是由于土体剖面非均质性造成了水流阻滞效应[5-6].基于均质土入渗理论，国内外很多学者对不同条件下不同质地组成的层状土壤入渗过程中湿润锋和累积入渗量进行了大量试验和理论研究[7-9]，但对运移过程中剖面含水量的试验观测和比较分析较少，尤其对相同质地不同土壤容重组成的层状土入渗研究还不多.

数学模型是研究层状土壤水分迁移规律的有效工具.前人在描述层状土壤水分迁移转化规律时为了简便起见，一般都设定土壤为单一土层分别模拟计算，再将土壤分层界面处设为一节点，界面处的参数分别按上、下两层参数的几何或算术平均计算，然后再人为地组合起来作为整体系统[10-11].这种方法对于解决饱和土壤中水分迁移转化取得了良好的效果，但对于非饱和土壤，由于受土层排序和耦合方式的影响[12]，组合起来的整体效果较差.杨艳等[13]求解对流-弥散方程得出，层状土的水动力弥散系数不是均质土水动力弥散系数的平均值.因此，层状土壤入渗过程及水分再分配模拟计算也不同于均质土壤.

南方第四纪红黏土典型土体构型为Ah-Bs-Csq型，土层自上而下土壤容重逐渐增加，土壤剖面结构分层明显.尤其是红壤坡耕地，其表层为耕作层，该土层比较疏松，土壤容重较小，透水透气性能较好；耕作层之下为犁底层，土层比较密实，水分渗透系数较小.因此，要精确地描述红壤入渗水分的迁移过程，必须要考虑土壤剖面容重分层问题.

文中通过室内土柱积水入渗试验和构建水分入渗数学模型，研究第四纪红黏土不同土壤容重的均质土及其组成的层状土壤的入渗特征和水分再分布过程.研究成果将不仅有助于揭示红壤丘陵区季节性干旱的形成机理，而且有助于促进非饱和带土壤水分入渗和迁移理论研究的发展，同时可为综合评价地表水、地下水资源、水土保持提供科学依据.

1 试验与方法

1.1 试验土样

试验土壤于2018年3月采集于江西省九江市德安县江西水土保持生态科技园内.该园区位于中国红壤的中心区域(115°23′～115°53′ E，29°10′～29°5′ N)，地貌类型属低丘岗地，海拔30～100 m，土壤类型为第四纪红黏土发育的红壤.试验将坡耕地0～40 cm表土取回至室内风干混合均匀，去除石砾和植物根系、枯枝落叶等杂质，过2 mm筛备用.采用EyeTech激光粒度分析仪测定试验土壤机械组成，测定结果为砂粒[2，0.05)mm含量17.43%，粉粒[0.05，0.002]mm含量60.43%，黏粒(<0.002 mm)含量22.14%，土壤为粉质黏壤土.

1.2 土层构型设计

试验土柱设计深度为40 cm，容重分别为1.35 g/cm3(A)和1.55 g/cm3(B)2种均质剖面土壤结构，以及上层20 cm厚容重为1.35 g/cm3和下层20 cm厚容重为1.55 g/cm3组合而成的层状土壤结构(AB)，每个处理重复3次.试验土柱采用干堆法分层装填.在每次装入W(g)土壤后，利用压实器进行土壤压实，使其达到规定的土壤土柱高度h.为了避免试验过程中土柱出现分层现象，需要把土层表面抓毛，再填下一层.装填后土壤A和B的初始体积含水率分别为8.35%和9.45%.

1.3 试验装置与过程

土壤入渗试验装置由带刻度供水容器(马氏瓶)、供水管、带刻度有机玻璃柱和土样组成，如图1所示，马氏瓶内径为8 cm，有机玻璃柱内径18 cm.马氏瓶与有机玻璃柱之间用连接管连接，调节马氏瓶位置及内管高度，保证恒定水头2 cm连续供水.柱底加一反滤体，其底部设有渗透收集装置.同时，在透明有机玻璃土柱侧面每间隔5 cm开孔插入TDR土壤水分传感器探头(LP/ms传感器)，连接数据采集器(TDR-MUX)用以每1 min自动记录入渗过程中土壤剖面含水率随时间的变化.当土柱底部出口有水流出时，停止供水，结束试验.为了克服马氏瓶刻度读数误差，试验过程中将马氏瓶放置在一个测量精度为0.1 g的电子秤上，试验进行时，电子秤的示数减小代表下渗的水量变化情况.根据由密至疏的时间原则记录电子秤读数.

图1 土柱入渗试验装置

1.4 模型模拟

采用HYDRUS-1D软件对3组试验土柱入渗过程进行数学模拟.若将坐标原点选在地面，取z轴向下为正，且忽略空气和温度对土壤水流运动的影响，则土柱一维薄层积水入渗非饱和土壤水分运移基本方程为

(1)

式中：θ为土壤体积含水率，%；t为时间，min；h为土壤基质势，cm；k(h)为土壤导水率，cm/min.

在对式(1)数值求解中，采用常用的van-Genuchten模型确定土壤水分特征曲线，其表达式为

(2)

(3)

(4)

m=1-1/n，

(5)

式中：θr为土壤残余体积含水率，%；θs为土壤饱和体积含水率，%；ks为土壤饱和导水率，cm/min；n为土壤形状参数；α为进气吸力；l为经验参数，一般取值为0.5.

模型初始条件根据TDR探头测定的土壤体积含水率设置；模型的上边界设为入渗过程中定压力水头(2 cm)，下边界条件设为自由排水.

2 结果分析

2.1 层状红壤水分入渗及运移过程模拟

根据实测土壤机械组成和装填土壤容重数据，利用HYDRUS-1D中的 Rasetta 人工神经网络模块预测各层van-Genuchten模型中土壤水力学参数并作为初始值.由于人工填土过程中，可能会造成下层土壤容重增大，而土壤饱和导水率随着容重增加呈现幂函数形式递减[14-16].因而，需要根据实际观测的土壤水分数据反演优化土壤饱和导水率ks[17-19]，从而得到各试验土柱的土壤水力学参数，见表1，表中ρ为土壤容重.

表1 各土柱土壤水力学参数

图2为层状土积水入渗水分再分布模拟结果，图中h′为土壤深度，向下为正.由图可知，均质土柱各层土壤水分观测值与模拟值间具有很好的一致性.容重为1.35和1.55 g/cm3土柱各层土壤水分的总体决定系数R2分别可达0.85和0.92，均方根RMSE误差分别为3.2%和1.8%，这表明HYDRUS-1D软件能较好地模拟均质红壤积水入渗过程及水分再分布规律.研究还发现，利用HYDRUS-1D对土壤水分再分布进行模拟时，在深层和土壤水分较高时误差较大.这可能是由于构建的HYDRUS-1D模型没有考虑土壤中滞锢空气作用造成的.随着水分入渗深度推进，滞锢土壤空气压力对入渗水流产生顶托与阻力作用越强.李援农等[20]和孙美等[21]已证实当土壤内部排气不畅时，易导致土壤水分模拟值与实测值之间存在较大差异.

图2 层状土积水入渗水分再分布模拟结果

对于层状土壤，简单组合均质1.35 g/cm3和1.55 g/cm3的土壤水力参数，模拟效果较差，各层土壤水分的总体决定系数仅为0.30，均方根误差达15%.吴奇凡等[9]研究也发现，利用均质土体反演的土壤水力参数直接模拟层状土体的入渗过程效果不理想.而对进气吸力参数α优化后，土壤水分模拟效果得到大幅提升，各层土壤水分的总体相关系数达0.87，均方根误差仅为2.8%.由此得出，对于层状红壤，积水入渗水分再分布模拟由各均质土水力参数简单组合起来的整体效果较差，需要对各层的进气吸力参数进行优化.参数α值越小，土壤进气值越大，土壤持水性能越大.与均质土壤的α值相比，层状上层土壤α值减少了2.24倍，下层土壤减少了1.49倍.由此可知，层状土壤结构使得土壤的进气值增大，土壤持水性能越大，尤其是对上层土壤.

2.2 层状红壤入渗特征

累积入渗量I和入渗速率i是表征土壤水分入渗能力的2个重要指标.均质型土壤的土壤水分累积入渗量和入渗率随时间变化过程均为连续平滑曲线，如图3所示.

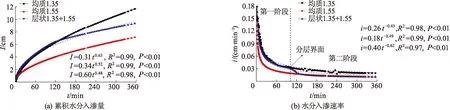
图3 不同土壤结构下水分累积入渗量和入渗速率过程

层状土入渗过程可明显分为入渗水分到达分层界面之前和之后2个阶段.第一阶段，开始时层状土壤累积入渗量和入渗速率随时间呈非线性增长，与上层均质土入渗过程基本无差异.第一阶段大致表示的是上层土壤的入渗性能曲线，也即土壤入渗性能还没有受到下层土壤影响.第二阶段，入渗水分通过分层界面后，累积入渗量随时间变化曲线发生了转折并趋于直线，土壤水分入渗率突发下降，然后趋于下层土壤稳定入渗率，土壤入渗进入下层土壤入渗阶段.该阶段上层土壤完全饱和，入渗性能完全由下层土壤控制.这是由于下层土壤容重突然变大，水分受土壤水势及下层土壤空气阻力影响下渗减慢.与均质土相比，上松下密层状土显著地提高了下层土壤的初始入渗速率，而对上层的入渗率和稳定入渗率影响不大.这是由于上层土壤容重小，土壤孔隙大，土壤水分传输能力大，能够快速为下层土壤供给水分.孙蓓等[22]对具有犁底层的农田入渗试验也发现，其水分入渗过程存在明显的耕层入渗阶段和犁底层入渗阶段.这与本试验得出的现象相一致.

进一步统计结果表明，均质型土壤累积入渗量与入渗时间的平方根呈显著线性关系，但组合后的层状土实测值与拟合曲线发生了明显偏离.均质土壤入渗速率与时间呈显著的幂函数关系(P<0.01)，但层状土的幂函数关系显著性有所减弱.

2.3 层状土壤水分再分布特征

水分再分布是土壤中的水分在水势梯度作用下的重新分布过程，是水分入渗的后续过程.图4为不同土壤结构的土壤水分分布.由图可知，在土壤质地和初始含水量相同的情况下，土壤容重对土壤水分入渗再分布模式影响微弱，均为随着水分入渗过程进行，各土柱从上至下土层含水率依次为陡升并趋于平稳的趋势.随着土壤重容增加，相同时间内土柱湿润体体积变小，土壤水分再分布过程变慢.例如积水入渗10 min后5 cm处，容重为1.35 g/cm3的体积含水率达35.06%，而容重为1.55 g/cm3的体积含水率仅为20.58%.

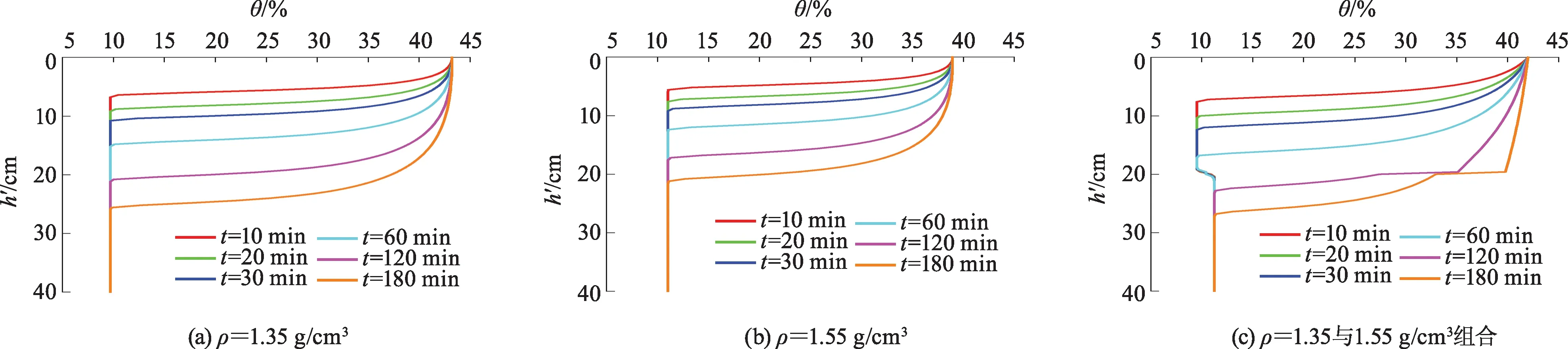
图4 不同土壤结构的土壤水分分布

层状土壤结构在湿润锋到达土层界面之前，土壤水分分布曲线形状与上层均质土壤基本一致.当湿润锋迁移至土壤分层界面处，土壤水分曲线出现不连续的突变现象，且上层土壤水分含量基本达到饱和.当土壤水分穿过分层界面后，土壤水分分布曲线形状与下层均质土类似.根据BODMAN等[23]的研究，当地表有积水入渗时，典型土壤水分再分布剖面由上而下可分为4个区，即表层饱和带、含水率变化大的过渡带、含水率分布均匀的传导层和湿润程度随深度减小的湿润层.随着入渗时间延续，传导层会不断向深层发展，湿润层和湿润锋也会下移，含水率分布曲线逐渐变平缓.由图4可知，红壤在初始较干旱的条件下，土壤表层的水势梯度较陡，入渗速率较大.在重力势、压力势和基质势的共同作用下，湿润锋迁移至分层界面时，土壤的基质吸力尚大于土层的进水吸力，其湿润锋在此出现停滞.随着入渗水量的补给，湿润锋处的土壤含水量逐渐增加，基质吸力逐渐降低，直到达到下层土的进水吸力时，湿润锋才开始穿过界面进入下层土体.在湿润锋到达土柱底部时，土壤内部的水分运动并没有结束，土壤水分在重力和基质势的综合作用下，由土水势高的地区继续向土水势低的地区运移.与均质土相比，层状结构土壤显著提高了上层土壤含水量.例如1.35 g/cm3均质土壤入渗30 min后10 cm处土壤体积含水率为19%，而组合层状土壤入渗30 min后10 cm处土壤体积含水量可达29%.这主要是上下层土壤容重差异导致渗透性、持水能力不同，在土层突变界面处产生水力阻滞作用.

3 结 论

1) HYDRUS-1D可很好地模拟均质土壤积水入渗过程中土壤水分的再分布过程.对于层状土壤，直接组合均质的土壤水力参数模拟效果较差，需要对进气吸力进行参数优化，优化后模拟结果良好.

2) 层状土壤积水入渗速率曲线可明显分为上层入渗阶段和下层入渗阶段.湿润锋在到达分层界前，土壤入渗率呈非线性减少；在达到界面后，土壤入渗曲线发生了转折，进入下层入渗阶段，并逐渐达到下层稳定入渗率.与均质土相比，层状土轻微降低了上层的入渗速率和提高了下层初始速率，但对下层的稳定入渗率影响不大.

3) 土壤容重对均质土壤水分入渗再分布模式影响微弱.与均质土相比，层状土壤可提高上层土壤含水量，且水分再分配过程在界面处发生了突变.