指向式旋转导向偏置机构方向控制及动力学仿真
2021-12-27吴泽兵蒋梦洁谷亚冰杨晨娟翟喜萍
吴泽兵,蒋梦洁,谷亚冰,杨晨娟,翟喜萍
西安石油大学机械工程学院
0 引言
旋转导向系统在超深井、高难定向井、水平井、大位移井、丛式分支井等油藏开发工艺井的导向钻井中发挥了重要作用[1-5]。目前世界上成熟的旋转导向钻井系统虽然种类较多,但按导向方式仅分为推靠式、指向式和推靠式+指向式三种[6-7]。其中,以贝克休斯的 Auto Track系统和斯伦贝谢的Power Drive系统为代表是推靠式旋转导向钻井系统,以哈里伯顿的Geo-Pilot系统和斯伦贝谢的Power Drive Xceed 系统为代表是指向式旋转导向钻井系统[8]。前期使效果显示,指向式系统较推导式系统具有较明显的优势:井眼更平滑、井身质量高及摩阻扭矩低等[9-10]。国内的研究工作起步较晚,于20世纪90年代中期开始,国内多家研究机构和大学相继开展旋转导向技术的研发工作[11]。进入21世纪,在国家“863”项目的支持下,中国石油集团、中国石化集团、中国海洋石油总公司等多家单位及相关大专院校在旋转导向关键技术方面取得了突破,先后研制出了推靠式的旋转导向系统,并在现场应用中取得了不错的效果[12-13]。而指向式旋转导向系统目前还处于现场试验阶段,在工具造斜率、井下工作可靠性等方面与国外技术相比仍有较大差距。为了打破长期被国外三大石油装备公司垄断局面,有必要开展深入研究。本文推导了芯轴轨迹方程可以得到任意时刻内外偏心环任意相对位置时芯轴的偏置方向,从而用来控制工具面的方位,可得到钻头的偏置角度,为精准控制钻头沿预定的轨迹钻进提供理论基础,对开发具有我国自主知识产权的指向式导向系统,大幅提升我国高精度导向钻井技术具有重要的意义[13-14]。
1 指向式导向系统的结构及原理
指向式旋转导向钻井工具主要组成为:钻杆、驱动连接器、旋转轴、上端密封、轴承组合、悬臂轴承、不旋转外套、偏心环组合、传动机构、调芯轴承和下部密封,如图1所示[13]。由图1可知,芯轴及其导向偏置机构在一个不旋转的外筒里进行工作,并通过密封圈与外界隔离开来,防止外界环境中的泥沙进入,造成机构的磨损,机构还可以通过注入润滑油的方式保护轴承等部件,延长系统寿命。
该系统的导向原理是通过偏心环组合之间的相互旋转,使旋转芯轴在弯曲强度允许的情况下挠曲,从而实现钻头的导向[8],如图2所示。
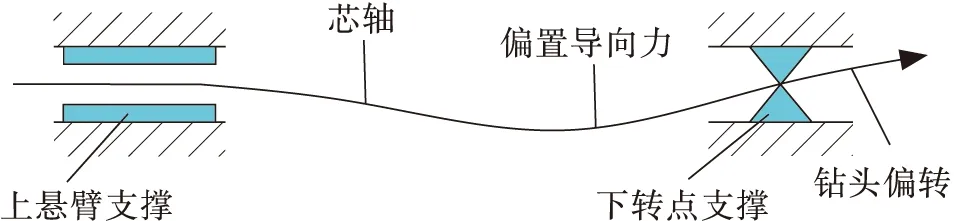
图2 指向式旋转导向工具工作原理示意图
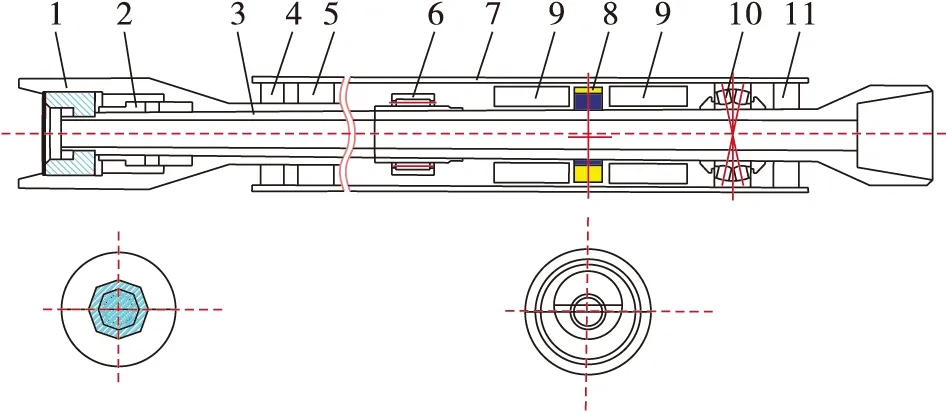
1.钻杆;2.驱动连接器;3.旋转轴;4.上端密封;5.轴承组合;6.悬臂轴承;7.外套;8.偏心环组合;9.传动机构;10.调芯轴承组合;11.下部密封。
2 系统主要部件的三维建模
本文使用了发展较为成熟的三维实体建模软件Creo,并采用了Creo自下而上生成装配体的方法。采用该方式的原因是:零部件是独立的,需要重新编辑零部件时,只需单独更改即可[15]。
根据力学优化结果,取偏置环组合距悬臂轴承的距离a=675 mm,取悬臂轴承与球轴承间的芯轴轴向距离L=1 m,芯轴外径D=50 mm,内径d=30 mm,钻杆外径121 mm,钻头外径152 mm。芯轴材料选用钛合金TC4,弹性模量E=1.13×1011Pa。
滚针轴承尺寸较小,承载能力好,可以较好的承受弯矩。因此,选悬臂轴承为NA6910型滚珠轴承,偏心环处为NK50/35型滚针轴承。
调芯球轴承具有自动调心功能,内、外圈轴线有一定偏转角度时(一般在3°以内)也可正常运转,因此球轴承选用22310型调芯滚子轴承。
设计完成后的装配模型主要由芯轴、钻杆、钻头、内外偏心环组合、调芯轴承、悬臂轴承、外筒等零部件组成。
3 导向系统动力学仿真
3.1 芯轴中心运动轨迹理论方程
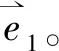
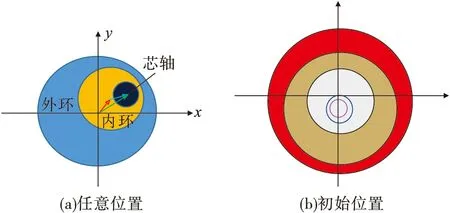
图3 偏置机构
根据图3(a)可知内外偏心环的合矢量为:
(1)
设垂直轴是y,水平轴是x,a1是e1与y轴正向夹角,a2是e2与y轴正向夹角,注意这里a2包含了a1,角度以顺时针方向为正,则合矢量在x、y轴上的分量X、Y分别为(本文中设e1=e2=e):
X=esinα1+esinα2
(2)
Y=ecosα1+ecosα2
(3)
为了使上述式(2)和式(3)满足偏置为零的初始状态,将α1=α1+180°,即将外环转180°,此时内外环偏心抵消,式(2)和式(3)变为:
X=-esinα1+esinα2
(4)
Y=-ecosα1+ecosα2
(5)
当a1和a2等于0时,X=0,Y=0,式(4)和式(5)满足初始位置条件。当a1和a2分别等于0°和180°时,即外环不动,内环转180°时X=0,Y=-2e有最大向下的偏移距,如图4所示;当a1和a2分别等于180°和0°时,即内环不动,外环转180°时X=0,Y=2e有最大向上的偏移距,如图5所示。

图4 偏心机构产生的垂直向下方向最大偏移位置
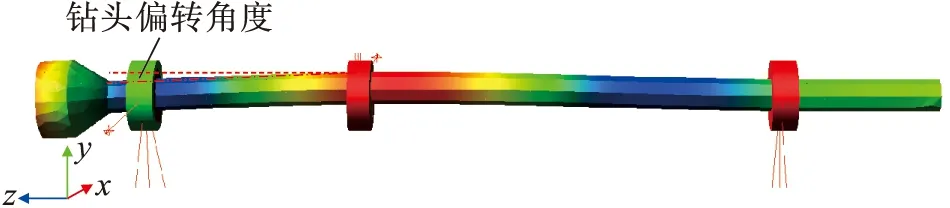
图5 偏心机构产生的垂直向上方向最大偏移位置
当a2=0,即内环静止,则式(4)和式(5)变为:
X=esinα1
(6)
Y=-ecosα1+e
(7)
当a1=0,即外环静止,则式(4)和式(5)变为:
X=esinα2
(8)
Y=-e+ecosα2
(9)
将式(8)和式(9)变成式(10),可以得到芯轴中心的轨迹形状。
X2+(Y+e)2=e2
(10)
式(10)从理论上说明了芯轴中心的运动轨迹是圆心在(0,-e),半径为e的圆[18]。
3.2 指向式旋转导向系统虚拟样机建立
本文采用虚拟样机仿真分析软件ADAMS对指向式旋转导向系统进行动力学仿真,对工作状态下的芯轴在偏心环旋转作用下的变形、受力的动力学分析。
利用ADAMS软件提供的约束库来给指向式系统的简化仿真模型施加约束。芯轴仿真模型中的各零部件之间添加的约束副如表1所示,设置接触对如表2所示。

表1 芯轴仿真模型中的约束副
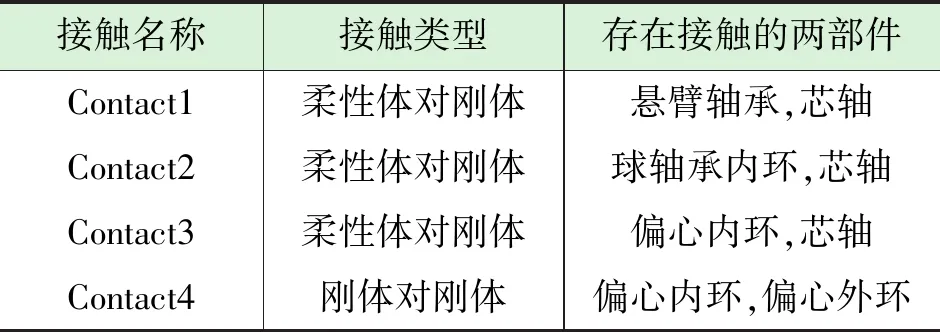
表2 芯轴仿真模型中的接触对
在ADAMS软件中,按照表1、表2添加约束副、设置接触对及其它边界条件得到芯轴的仿真模型,如图6所示。

图6 指向式旋转导向机构芯轴仿真模型
芯轴在偏置机构处横截面中心运动轨迹有三个关键位置,即两个极端位置:芯轴在偏心环作用下向上变形最大,如图5所示;向下变形最大如图4所示;还有一个中间位置,即系统的初始位置。根据矢量位移幅值和导向系统的几何结构可以得到钻头实际的偏离井眼中心的角度,如图4和图5所示。
利用ADAMS还可以输出内环受芯轴变形产生力的三个分量随时间的动态变化曲线,如图7所示。

图7 内环受力三个分量动态变化曲线
3.3 芯轴偏置运动轨迹仿真
为验证上述推导芯轴中心运动轨迹方程的正确性,将计算结果与ADAMS仿真结果进行了对比。
以上面的外环静止,内环转动如式(8)和式(9)为例,改变内环的位置,即逐渐增大内环的转角a2,分别计算芯轴的中心坐标分量X、Y,然后计算位移幅值、位移方向,另外利用ADAMS仿真得到内外环在不同旋转角度时内环受力在X、Y方向的分量,以及芯轴中心X、Y分量,最后计算力幅值及力的方向,以及计算的芯轴位置分量与仿真的位置分量之间的相对误差,具体见表3所示。

表3 外环静止内环旋转情况下理论计算结果与ADAMS仿真结果比较及误差
从表3可以看到,芯轴的偏置方向的理论计算值与ADAMS的仿真值基本一致,而且理论计算得到的芯轴X、Y分量与ADAMS仿真得到的基本一致,除一例外误差均小于5%。
另外通过计算还得到芯轴或钻头偏置方向与内环转角呈线性关系,即偏置方向是内环转角的一半加上90°,如图8所示。具体举例来说明:当外环静止,内环逆时针转80°,那么此时芯轴的偏置方向为80°/2+90°=130°,如图9所示。但要注意的是角度是以y轴正向为起点,逆时针方向计算的。

图8 芯轴偏置方向与内偏心环转角关系

图9 偏置机构偏转方向
不同的偏置机构初始状态,有不同的偏置方向与内环或者外环旋转角度的线性关系方程。如果内外环同时旋转,则利用式(4)和式(5)可以得到芯轴中心在任意时刻的位置,即可得到偏心环处芯轴的偏移值和偏转方向,亦即可得到工具面钻头的偏转方向。
表4是利用推导的芯轴运动轨迹方程计算X,Y分量与ADAMS软件仿真结果进行的比较。从表4中记录的两个验证实例可以观察到,计算的偏心环处芯轴的偏移值和仿真的相对误差较小,计算的偏心环处芯轴偏转方向也和仿真的内环受到合力方向基本一致。因此,完全可以利用本文中的理论计算任意尺寸组合的两偏心环构成的偏置机构的偏置方向,编程后植入旋转导向系统的控制模块,能够通过快速计算实时获得要求的钻头的偏转方向。当然,与设置的工具面中钻头偏置方向对应的内外偏置环相对位置可能不止一个组合,但可以编程计算找到花时间最短的那个组合。

表4 内外环同时旋转情况理论计算结果与ADAMS仿真结果比较及误差
内外偏心环的相对转动会引起芯轴发生不同挠度的挠曲变形,然后带动与芯轴连接的钻头发生偏转,并且在理论上钻头偏转方向与偏心环处芯轴偏置方向相反且角度相同。以外环静止,内环转动为例,利用本文推导的芯轴轨迹式(8)和式(9),计算芯轴偏移角度和位移方向,即可得到工具面钻头的偏转角度和位移方向。表5是利用推导的芯轴运动轨迹式(8)和式(9)计算芯轴偏移方向与ADAMS软件仿真的钻头偏移方向结果的比较。
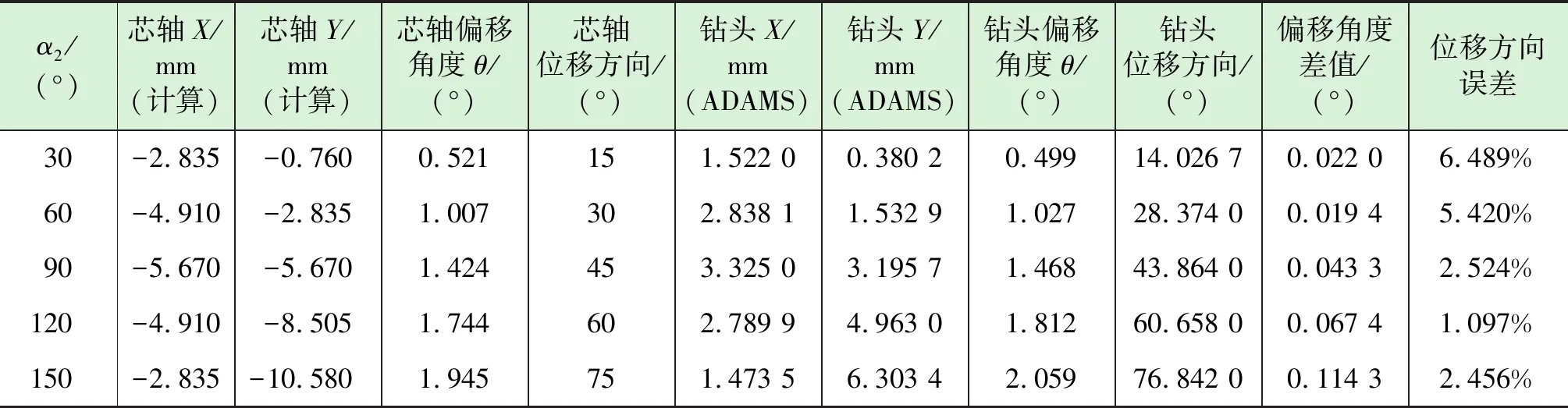
表5 外环静止内环旋转情况钻头偏置方向理论计算结果与ADAMS仿真结果比较
从表5中可以看出芯轴偏置与通过ADAMS仿真得到钻头工作面的偏置方向基本一致,但在期望钻头偏移角度大于2°的情况下,计算与仿真的偏移角度差值超过0.1°,可能是由于一般芯轴挠曲转角θ最大在1°~2°之间,当挠曲转角过大时,芯轴承受的弯曲应力过大导致的误差增大。在工程应用上,一般选取芯轴的挠曲转角不会大于1.7°,仿真与计算的钻头偏移角度差值均小于0.1°。因此,这在工程上是完全可行的。
从前面的理论计算和ADAMS仿真对比分析可以得到:本文推导的芯轴轨迹式(4)和式(5)是正确的,利用该方程可以得到任意时刻,即内外偏心环任意相对位置时芯轴的偏置方向,亦可得到钻头工具面的偏转方向,编程后用来快速得到控制工具面的方位,精确制导钻头沿预定的轨迹钻进。
4 结论
(1)本文简要介绍了常见的指向式旋转导向系统的结构及工作原理;推导了双偏心环运动轨迹芯轴中心运动轨迹方程、内外偏心环的运动轨迹和芯轴中心分量之间的运动关系式,并计算了在不同条件下的理论偏移分量。
(2)利用CAD软件Creo建立了简化的指向式旋转导向系统的三维模型,基于该数字模型在ADAMS软件建立了有限元动态仿真模型,并仿真得到了内外偏心环的运动轨迹和芯轴中心分量之间的运动关系,验证了推导公式的正确性;比较了理论值和ADAMS软件仿真得到的数值解,两者80.56%数据的相对误差都小于7%,验证了推导轨迹公式在工程应用上的可行性。
(3)本文推导的芯轴轨迹公式可以得到任意时刻,即内外偏心环任意相对位置时芯轴的偏置方向,并且可以实时计算钻头的偏转角度,从而用来控制工具面的方位,为精确制导钻头沿预定的轨迹钻进提供了理论基础,为指向式旋转导向系统的偏置机构控制程序模块开发提供了理论模型,因此具有重要的实际意义。
