我国3种针叶林的材积源生物量模型研建

曾伟生

(国家林业和草原局调查规划设计院，北京 100714)

森林生物量与森林蓄积量一样，既是各级森林资源监测的重要指标，更是反映森林生态系统生产力的重要参数[1-3]。对森林生物量的估计，既可通过建立立木生物量模型来获得[4-5]，也可通过建立林分生物量或生物量转换因子模型来获得[2,4]。根据Luo等[6]的综述，1978年至2013年间，我国学者已发表了近200个树种的5924个立木生物量模型。2014年以来，国家林业局有计划地编制了我国主要树种的立木生物量模型，并颁布实施了系列行业标准[7-13]。但是，不论是国外[5,14-20]还是国内[21-28]，发表的林分生物量模型都要显著少于立木生物量模型。

在已有的林分水平模型中，影响最大的是方精云等[21-22]发表的21种森林类型的材积源生物量模型，该模型在很多研究中得到了引用[27,29-32]。此外，王斌等[24]利用1266个不同森林类型样地的数据，建立了我国16种森林类型的生物量与蓄积量之间的双曲线模型。经分析，这些模型存在3个方面的不足：一是建模样本较少，大部分模型都是建立在小样本基础上。如方精云等[22]建立的21个模型有18个（仅落叶松、油松、杉木除外）的建模样地数在30 以下，王斌等[24]建立的16个模型有10个的建模样地数在50 以下。二是建模方法简单，基本都是采用普通最小二乘法，未考虑生物量和蓄积量数据的异方差性。三是评价指标单一，仅提供了确定系数R2[22]或相关系数R[24]这一项评价指标，未提供其他误差方面的评价指标，其适用性存疑。因此，对林分生物量建模方法做进一步研究是非常必要的。

本研究利用我国3种主要针叶林（落叶松Larixspp. 、油松Pinus tabulaeformisCarr.、杉木Cunninghamia lanceolata(Lamb.) Hook.）的3000个样地的地面实测数据，采用加权回归估计[33]和分段建模方法[34]，建立林分水平的材积源生物量模型，既为这3种森林类型的生物量调查提供计量依据，也为规范林分生物量建模方法提供科学参考。

1 数据与方法

1.1 数据资料

本研究所用数据为第九次全国森林资源清查的固定样地调查资料，涉及我国3种主要的针叶林类型，即：落叶松林、油松林和杉木林。按优势树种（占65%以上）确定的这3种类型的针叶林，全国的有效样地数（蓄积量大于0）分别为2490、1185和3152个，每个样地都基于每木胸径测量数据，采用一元立木材积模型和立木生物量模型计算出蓄积量和生物量（包括地上生物量和地下生物量）。由于样地数主要集中在每公顷蓄积量和生物量较小的区段，为了保证所建模型具有广泛适用性，将全部样地按每公顷生物量大小用上限排外法分为4级（<50，50～100，100～150，≧150 t·hm−2），按每级样本量尽量均等的原则[35-36]选取建模样本，每公顷生物量150 t 以上的样地数相对较少，尽可能多选一些用作建模样本，剩下的样地作为检验样本。经综合考虑，最后确定3种林分类型选取建模样地分别为1200、800 和1000个。表1 是3种针叶林分的建模样地数和检验样地数按每公顷生物量等级的分布情况，图1 是根据全部3000个建模样地数据绘制的散点图。

表1 3种针叶林分的建模样本数和检验样本数Table 1 The number of modeling plots and validation plots for three coniferous forest types

图1 全部建模样地生物量与蓄积量散点图Fig.1 The scatterplot of biomass vs.volume for all modeling plots

1.2 建模方法

将基于前述3种针叶林3000个样地的蓄积量、生物量实测数据，首先分别普通回归和加权回归，建立林分生物量模型，并分析其建模效果，最后再用分段建模方法，建立估计效果更好的生物量模型。

1.2.1 回归估计方法 林分生物量主要与林分蓄积量有关，基于蓄积量的生物量模型应用最为广泛[21-22,24,27,29-32]。根据方精云等[22]对全国21种森林类型的研究结果，林分生物量与蓄积量之间呈线性相关。从3000个样地的每公顷生物量与蓄积量数据的散点图分析，这种线性相关规律也是非常明显的（图1）。因此，本研究确定采用如下线性形式的林分生物量模型：

式中：B为每公顷生物量（t·hm−2），V为每公顷蓄积量（m3·hm−2），a0、b0为模型参数，ε1为误差项，假定其服从均值为0 的正态分布。将（1）式两边除以V，可得到如下林分生物量转换因子模型：

式中：BCF为生物量转换因子（=B/V），c0、d0为模型参数，ε2为误差项。式（2）为非线性模型，如果设定y=BCF，x= 1/V，则可以转为以下线性模型：

上述模型（1）、（3）的参数可采用普通线性回归估计方法求解。根据对模型的结构分析，模型参数之间理论上应该存在以下关系：

事实上，模型（2）、（3）的拟合结果，就相当于模型（1）的加权回归结果，其权函数为w=1/V。因此，根据实际的拟合结果，式（4）必然是不成立的。由于生物量数据与蓄积量数据类似，都具有异方差性，模型（1）应该采用加权回归估计才是合适的[33,37]。参照有关权函数的研究结论[37]，权函数w= 1/V效果不一定最好，更通用的权函数应为w= 1/Vk，其中k一般在0.5～1.0 之间。

为了区别，这里将生物量模型（1）的拟合方法称为普通回归，生物量转换因子模型（2）或（3）的拟合方法称为加权回归1（权函数w1=1/V），以模型（1）为基础进行的加权回归估计方法称为加权回归2（权函数w2= 1/Vk）。

1.2.2 分段建模方法 当变量的取值范围很大时，用一个模型通常难以对各个区段都作出准确估计，解决这一问题的有效方法就是分段建模。在建立单木水平的生物量模型时，就已经有人用到了这一方法[34]。林分生物量的建立，同样可能碰到这一问题。假设最小的区段（如每公顷蓄积量50 m3·hm−2以下）存在明显偏估，就可以将自变量V=50 m3·hm−2置为两个模型的链接点，并将适用于V<50 m3·hm−2的模型参数设定为a1和b1，适用于V≧50 m3·hm−2的模型参数设定为a2和b2。为了保证两个模型在链接点的估计值一致，先拟合其中一个模型的2个参数后，另一个模型2个参数的估计就要受到这一条件的约束，其中只有一个参数是独立估计的，另一个参数直接根据（5）式由其他3个参数推出。

根据两个分段模型拟合的先后顺序，可以得出2 组分段模型：

式（6）是先拟合适用于V<50 m3·hm−2的模型参数a1和b1，再拟合适用于V≧50 m3·hm−2的模型；式（7）是先拟合适用于V≧50 m3·hm−2的模型参数a2和b2，再拟合适用于V<50 m3·hm−2的模型。通过对比其评价指标的优劣，选定拟合效果较好的模型。

1.2.3 模型评价方法 用于模型评价的指标包括以下6 项：确定系数R2、估计值的标准差（也称剩余标准差）SEE、总体相对误差TRE、平均系统误差ASE、平均预估误差MPE和平均百分标准误差MPSE[38-39]。其中MPE和MPSE的计算公式如下：

式中：yi为实际调查值，为模型预估值，为样本平均值，n 为样地数，tα为置信水平α 时的t 值。对建立的回归模型，计算以上6 项指标值，根据指标大小进行模型评价。

从实用性角度考虑，一般要求模型的TRE和ASE均在 ± 3%以内，MPE小于3%，MPSE小于15%。另外，残差图也是评价模型的重要参考依据。一个好的模型，残差应当呈随机分布。也就是说，模型每个区段的总体相对误差TRE都应该相差不大，一般应在 ± 5%以内。为了评价模型的广泛适用性，还采用检验样本进行独立交叉检验，计算模型的总体相对误差TRE是否在允许误差范围内。

2 结果与分析

利用3种针叶林的3000个样地的每公顷蓄积量和生物量数据，分别采用普通回归、加权回归1（权函数w1= 1/V）和加权回归2（权函数w2=1/Vk）拟合线性生物量模型（1），其拟合结果和评价指标见表2。

从表2 可以明显看出，不论是2个参数的估计值还是6 项评价指标，加权回归2 的结果都居于普通回归和加权回归1 之间，且更接近加权回归1 的结果，唯有TRE和ASE这2 项指标比较特殊：普通回归TRE为0，ASE较大；加权回归1 则ASE接近于0，TRE较大；而加权回归2 则处于折中状态，TRE和ASE都与0 相差不大，尽可能同时控制在预定的误差范围内（如 ± 3%以内）。尽管从R2、SEE和MPE这3 项指标看，普通回归模型要好些，但从ASE和MPSE看，则普通回归模型要显著差些。最后，再来看另外一项重要指标总体相对误差TRE，为了更深入了解模型在不同生物量等级的拟合效果，表3 分别落叶松、油松和杉木按建模样本和检验样本列出了总体和各个生物量等级的TRE。

表2 林分生物量模型的参数估计值和模型评价指标Table 2 The parameter estimates and evaluation indices of stand-level biomass models

从表3 可以看出，不论是考虑建模样本还是检验样本，加权回归模型的结果都要优于普通回归模型，而加权回归模型2 又要略优于加权回归模型1。因此，从模型本身特性、6 项评价指标及独立检验结果综合考虑，应当采用加权回归模型2 的拟合结果。

然而，如果再仔细查看表3 中加权回归模型2 在各个生物量等级的TRE（加粗的部分），发现还是存在一些不足，如：生物量小的区段总体上表现为正偏，而生物量大的区段总体上表现为负偏（油松相反）；部分区段TRE较大，超出了 ± 5%的范畴。根据对残差图所作的分析，生物量小的区段容易出现较大偏差，因此，如果采用分段建模方法，应该能提高预估精度。综合考虑样本量的支撑程度和规范统一性，本研究将自变量V= 50 m3·hm−2设置为分段建模的链接点，同时建立了式（6）和式（7）两套模型，拟合结果见表4，基于建模样本和检验样本计算的各个生物量等级的总体相对误差TRE见表5。

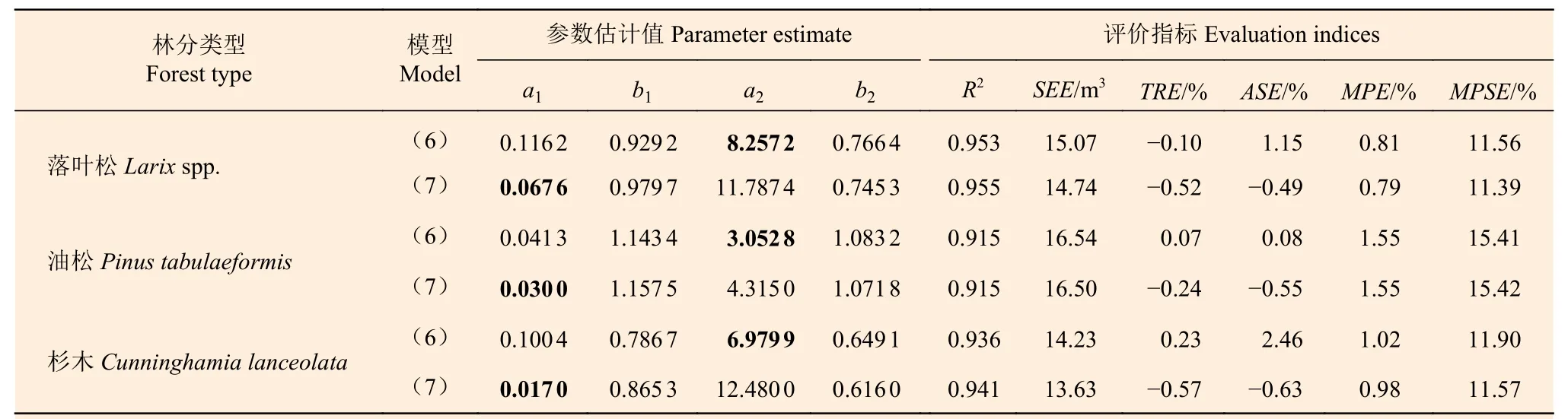
表4 分段建模的参数估计值和模型评价指标Table 4 The parameter estimates and evaluation indices of segmented biomass models

表5 分段生物量模型的总体相对误差Table 5 The total relative errors of segmented biomass models

从表4 的6 项评价指标看，模型（6）和（7）之间的差异不明显；但从表5 的对比可以看出，模型（6）明显优于模型（7），每个生物量等级的误差基本都在 ± 5%以内。除油松的分段模型改进甚微外，落叶松和杉木的分段模型有显著改进，杉木分段模型各生物量等级的误差甚至达到了 ± 2%以内。因此，综合考虑模型的各项评价指标及检验结果，最终选定分段模型（6）作为3种针叶林分的生物量估计模型。

3 讨论

本研究针对我国在林分生物量建模方面存在的样本数量偏少、建模方法简单、评价指标单一等问题，基于第九次全国森林资源清查3000个固定样地的实测数据，综合利用加权回归方法和分段建模方法，建立了落叶松、油松、杉木3种主要针叶林的每公顷生物量模型。最终确定的分段回归模型如下：

其确定系数R2在0.915～0.953 之间，平均预估误差MPE在0.81%～1.55% 之间，平均百分标准误差MPSE在11.56%～15.41%之间。林分生物量与蓄积量呈线性相关，这与方精云等[22]的研究结论是一致的。但是，由于在样本数量、建模方法等方面存在的差异，模型的适用性肯定会有很大不同。在引言中提到方精云等[22]建立的21个林分类型的生物量模型，建模样本数量在30 以上的仅有以下3个模型：

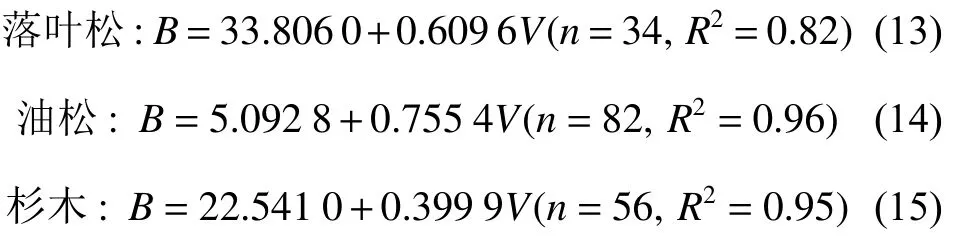
表6 列出了利用本研究所收集的全部样地对这3个模型的检验结果。可以看出，3个模型不仅总体的TRE远远超出了允许误差范围，不同生物量等级的估计值更是存在非常大的系统偏差。通过与本研究所建模型参数进行对比，发现式（13）～（15）的截距参数都要偏大，而斜率参数都要偏小，这正是对蓄积量小的样地会产生正偏而对蓄积量大的样地会产生负偏的直接原因。之所以其参数估计值出现大的偏差，主要原因应该是参数估计方法不恰当，采用的是普通回归而不是加权回归。其次，样本量的大小及样本结构的好坏也是影响因素之一。笔者曾试图系统抽取表1 中全部样本的2/3 建模、1/3 检验，尽管建模样本数量大幅增加，但因为样本结构不理想，建模结果并未达到预期要求。因此，建模成功的要素，一是样本数量足够；二是样本结构合理；三是建模方法科学。表6 也列出了利用全部样本对本研究所建模型的检验结果，总相对误差都在 ± 1%以内，各个生物量等级的估计误差大都在 ± 5%以内，最大的也未超出 ± 10%的范围。这样的模型，才是适用性广的模型。

表6 不同生物量模型总体相对误差的对比Table 6 The comparison of total relative errors of different biomass models

图2 展示了落叶松生物量模型（10）和模型（13）的残差分布，可以看出，因为模型（13）的截距参数a0= 33.8060，会得出每公顷蓄积量为0 的落叶松林其生物量高达33.8 t·hm−2的结果，从而导致每公顷蓄积量较小的林分，其生物量估计结果出现正偏；每公顷蓄积量较大的林分，其生物量估计结果出现负偏。其他2个树种的生物量模型（11）、（12）与模型（14）、（15）的残差分布对比情况也类似，为省篇幅，不再列出。

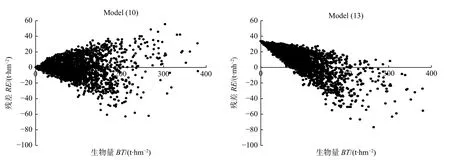
图2 落叶松生物量模型（10）和模型（13）的残差分布对比Fig.2 Comparison of residual errors between model (10) and (13) for larch

4 结论

根据本研究的相关结果，可以得出以下结论：（1）林分每公顷生物量与蓄积量呈线性相关。（2）建立林分生物量模型，应当采用加权回归方法；当一个模型难以准确估计各个等级的生物量时，可以采用分段建模方法。（3）样本数量和样本结构是除建模方法之外影响建模效果的另外两个重要因素。（4）本研究所建3种针叶林的生物量模型，预估精度高，可以在实践中推广应用。

最后需要补充的一点是，本研究只是基于优势树种划分的林分类型分别建立材积源生物量模型，没有再分树种组成按绝对纯林（占90%以上）和相对纯林（占65%～90%）分别建模，也没有分起源按天然林和人工林分别建模。因此，用于预估更细的类型时模型的误差肯定会有所增加。若想进一步提高模型的预估精度，可以分别天然林、人工林和绝对纯林、相对纯林建模，或将起源、纯林类型等因子按哑变量对待，建立适应性更广的哑变量模型。另外，本研究所建材积源生物量模型是以立木生物量模型的估计结果为基础建立的，属于林分水平的模型；与单木水平的模型相比，其预估精度要略低[40-41]。模型应用时，若具备单木水平模型的应用条件，应该首先采用单木模型；若只有样地、林分或小班水平的数据，不具备单木水平模型的应用条件，才考虑采用林分水平模型。