高速铁路无砟轨道-路基动力响应及病害分析
2021-12-27邢文茂赵丽华张吉松
邢文茂 赵丽华 张吉松
(1.中铁工程设计咨询集团有限公司太原设计院,太原 030013; 2.大连交通大学土木工程学院,大连 116028;3.北京交通大学轨道工程北京市重点实验室,北京 100044)
目前,国内外研究人员从理论分析、数值模拟、现场试验等方面对高速铁路无砟轨道-路基动力响应进行大量研究,并取得许多相关成果。戴鑫认为应考虑CA砂浆粘弹性,将CA砂浆定义为弹性或粘弹性时,其对轨道结构的影响也不尽相同[1];王启云釆用理论分析、数值模拟和模型试验对无砟轨道-路基的动力特性进行研究[2];任娟娟等探索在列车疲劳荷载作用下,板式无砟轨道CA砂浆粘弹性特征[3];薛富春等建立精细化的足尺轨道-路基-地基耦合系统非线性数值分析模型,研究动荷载引起的轨道-路基中位移、应力、加速度的分布规律[4]。
然而,系统结构在列车高速行驶时的动态力学响应非常复杂,目前针对无砟轨道-路基的研究大多集中在轨道结构的动力特性方面,而往往忽略了轨道-路基的分层特性。CA砂浆由水泥、乳化沥青、砂和多种外加剂组成,其主要原料乳化沥青属于黏弹性材料,具有蠕变和应力松弛的特征。CA砂浆作为轨道板与底座板之间的连接层材料,发挥传递荷载、调整支承的重要作用[5-6]。当考虑CA砂浆黏弹性时,将地基视为弹性基础;而当考虑地基的弹塑性时,又将CA砂浆视为弹性。
考虑CA砂浆黏弹性特征以及路基土材料的非线性,通过建立轨道-路基-地基大耦合系统,探究动荷载作用下系统的动力响应变化规律,分析车速、轴重、扣件刚度对系统动力响应的响应,同时通过模拟路基结构的一种病害,研究路基结构发生病害时对系统动力响应的影响。
1 建立模型
以哈尔滨—大连高速铁路某区间(设计速度350 km/h)无砟轨道-路基结构为研究对象,基于CRTS I型板式无砟轨道建立无砟轨道-路基模型(如图1所示),模型由钢轨-轨道板-CA砂浆层-底座板-基床表层-基床底层-路基本体-地基组成,纵向长15 m,横向宽30 m。

图1 高速铁路无砟轨道-路基结构模型
钢轨采用标准60 kg/m新轨截面。结构部分均采用实体单元模拟,扣件通过弹簧来模拟,部件之间的接触作用通过tie连接定义[7];对钢轨截面、轨道板截面、底座板截面、基床、路基、地基两端施加沿纵轴方向的对称约束[8]。为满足动力响应计算的稳定性,钢轨的网格需要划分得足够小,这将大幅增加计算规模。为减小计算量,钢轨、轨枕、扣件、轨道板、CA砂浆层和底座板只取下行线部分[9]。
受应力集中及边界效应的影响,建立3块轨道板长度的轨道模型,取中间板的数值模拟结果分析,钢轨、扣件系统、轨道板和底座板,均采用线弹性本构模型;CA砂浆层赋予弹性及黏弹性两种属性,黏弹性参数采用修正Burgers模型转化的Prony级数输入,依据室内30 ℃单轴压缩蠕变实验结果计算获得,其中CA砂浆采用的瞬时弹性模量为7.125 MPa[10];土体材料赋予弹性及弹塑性两种属性,弹塑性采用理想Drucker-Prager本构模型[11]。模型尺寸与材料参数如表1所示。

表1 结构模型尺寸及材料参数
目前,大量学者将列车振动引起的随机荷载用静荷载和由若干正弦函数叠加而形成的动荷载两部分的激振力函数来模拟[12]。在考虑振动荷载产生机理和速度、线路不平顺、矢高、轮重等因素的基础上,对已有表达式进行修正和完善,得到高速列车振动荷载的模拟表达式,有
F(t)=P0+P1sinw1t+P2sinw2t+P3sinw3t
(1)
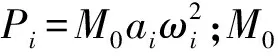
2 结果分析
图2~图5为无砟轨道-路基模型各结构层的应力云图,由图可知,轨道板局部地区应力的数量级最大达到106,其余地方数量级则为105,应力向下逐渐衰减,在路基处应力的数量级为102。

图2 轨道板应力云图
对于轨道结构部分,从图2中可以看出,轨道板外围应力偏大,这是由于在荷载作用下轨道板向下挤压,而底座板抵抗轨道板的挤压,故在轨道板外围形成了回弹,导致应力增大。其次,在各个扣件处都有一个应力增大的圆形范围,中间轨道板尤为明显,这是由于扣件对钢轨的扣压作用,动荷载作用下,钢轨不停振动,扣件约束保证了钢轨的稳定性,故在轨道板上可以看到扣件处应力较大。
从图3中可以看出,轨道板中间的CA砂浆层由于受到了列车荷载的作用,四个边角的应力较其他地方明显增大,这也说明CA砂浆层的四个边角容易受到破坏。当边角应力增大时,由于受到挤压,CA砂浆层中部位置隆起出现了初始的裂缝。在自然环境中,雨水等物质不断侵蚀CA砂浆层,同时,在荷载作用下会受到轨道板长期拍打,后期达到一定的疲劳强度,逐渐产生CA砂浆层与轨道板局部脱空,甚至完全脱空。因此,需做好该位置的监测和保护,以免长期疲劳荷载后,造成更大的影响。

图3 CA砂浆层应力云图
对于路基结构部分,从图4可以看出,基床表层的整体应力已经衰减到102数量级,中间轨道板处的应力较其他地方大,在中间轨道板中四个边角的应力最大。同CA砂浆层受力类似,基床表层受底座板的挤压,而使得边角应力增大。

图4 基床表层应力云图

图5 基床底层应力云图
从图5可以看出,基床底层应力分布较为均衡,中间轨道板和路基边坡应力较大。轨道板呈现“工”形的应力分布;而路基边坡的应力分布则是从钢轨中点向两侧延伸。这是由于定点加载的激振力荷载,使得施力点处横断面应力都偏大。路基本体的应力分布变得更加均衡,在中部位置应力略大。地基处应力最小已经降至16.09 Pa,此时动荷载对地基各部分的影响可以忽略不计。
3 不同构件参数对轨道结构的影响
高速铁路的运营管理规程中,对轨道结构的变形有严格要求,而轨道结构的变形取决于无砟轨道与路基的变形,尤其是基床结构的变形。目前,我国高速铁路路基的强度控制要求基床表面的动应力不大于填料的允许应力,动变形控制要求路基面动位移不大于3.5 mm[13]。通过分析影响轨道-路基变形的重要参数,探讨构件参数对系统动力响应的影响程度,研究车速、轴重和扣件刚度对无砟轨道-路基系统的动力响应影响,为设计出动力性能更加优越的无砟轨道-路基提供参考资料。
随着列车速度的不断提升,车体对轨道结构的振动影响不断增大,各项指标也有所变化。本次主要选取200 km/h、250 km/h、300 km/h、350 km/h的竖向动位移指标进行对比分析。
轨道结构最不利位置的竖向动位移峰值如图6所示。当车速为200 km/h时,轨道板的竖向动位移峰值为0.349 mm,当速度350 km/s时为0.408 mm,增幅达到16.9%;当速度为200 km/h时,底座板的竖向动位移峰值为0.331 mm,当速度350 km/s时为0.378 mm,增幅达到14.2%。从图6可以看出,随着速度的增加,竖向动位移不是简单的增大,而是有着某种变化规律。由于研究中仅读取4个速度值的数据,不能看到连续变化的规律。根据梁波等的相关研究[14],列车车速对轨道-路基结构竖向动位移的影响并不是简单的正相关关系,而是会有明显的突变,即随着车速的不断增大,竖向动位移呈现明显的双峰现象(在180 km/h和370 km/h处达到极值)。因为200 km/h和350 km/h分别接近两端的极值,位移在两极值之间会出现一段低谷,所以在180 km/h达到极值后位移将会先减小再增大,故在图中200 km/h到350 km/h之间呈现出先减小后增大的规律。
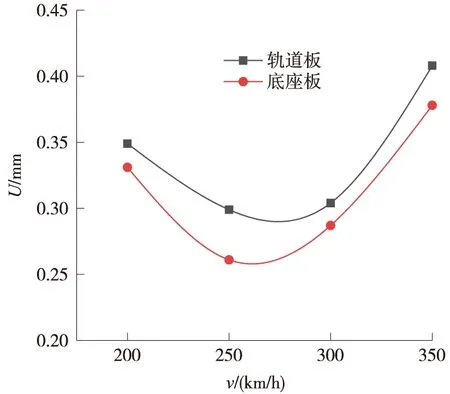
图6 竖向动位移峰值随车速的变化
我国的重载铁路发展迅速,大秦铁路、朔黄铁路、瓦日铁路、蒙华(浩吉)铁路等一批重载铁路运输通道相继开通,为我国的货物运输提供有力保障。随着我国铁路重载化趋于成熟,车辆轴重对无砟轨道-路基系统的影响,也是必须要考虑的一部分。
轨道结构最不利位置的竖向动位移峰值如图7所示。从图7可以看出,轨道结构竖向动位移峰值随着车辆轴重的增加而变化,各项动力响应指标都在不断增大。对于轨道板的竖向动位移峰值,当车辆轴重为150 kN时为0.408 mm,而当车辆轴重为220 kN时为0.524 mm,增幅达到28.4%;对于底座板的竖向动位移峰值,当车辆轴重为150 kN时为0.378 mm,而当车辆轴重为220 kN时为0.489 mm,增幅达到29.4%。轴重增大时位移也在增加。因此,路基的沉降是首要解决的问题之一,铁路建设中应处理好路基的稳定性问题。
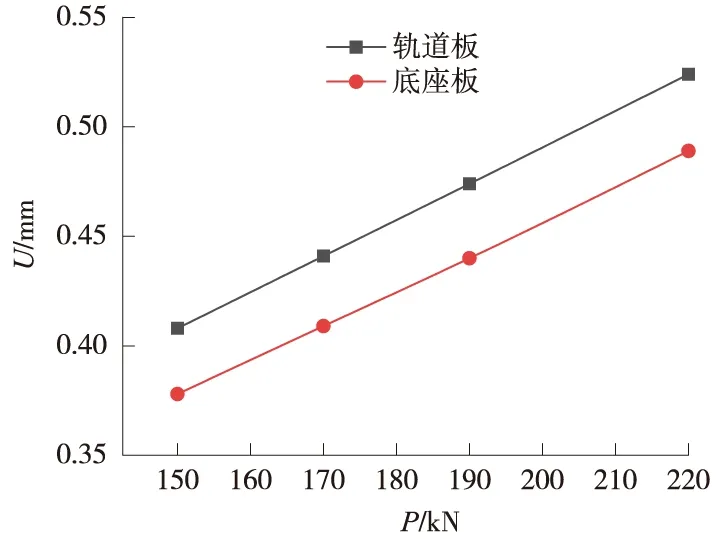
图7 竖向动位移峰值随轴重的变化
在列车运行过程中,车体与轨道间的长时间震动,导致轨道结构的扣件松动,如果完全脱落,将产生非常大的风险。因此,铁路部门会定期调整扣件的松紧,而扣件刚度的大小,也会产生不同的动力响应结果。本次选用20 kN/mm、35 kN/mm、50 kN/mm、65 kN/mm垂向扣件刚度进行对比分析。
轨道结构最不利位置的竖向动位移峰值如图8所示。从图8可以看出,随着垂向扣件刚度的增加,各结构层的竖向动位移峰值都在不断增大。这是因为扣件刚度的增加,使得钢轨对轨道的扣压力不断增大,使得传递到下部结构的动应力增大,各结构层动力响应指标值也会相应增大。对于轨道板的竖向动位移峰值,当扣件刚度为20 kN/mm时为0.326 mm,而当扣件刚度为65 kN/mm时为0.425 mm,增幅达到30.3%;对于底座板竖向动位移峰值,当扣件刚度为20 kN/mm时为0.305 mm,而当扣件刚度为65 kN/mm时为0.393 mm,增幅达到28.8%。从上述分析中可以看出,在保证钢轨的位移符合相关规定的同时,采用较低刚度扣件对于降低无砟轨道-路基系统结构的动力响应有利,可以显著降低无砟轨道-路基系统的振动响应,故适当采用低刚度扣件可以达到减振作用。
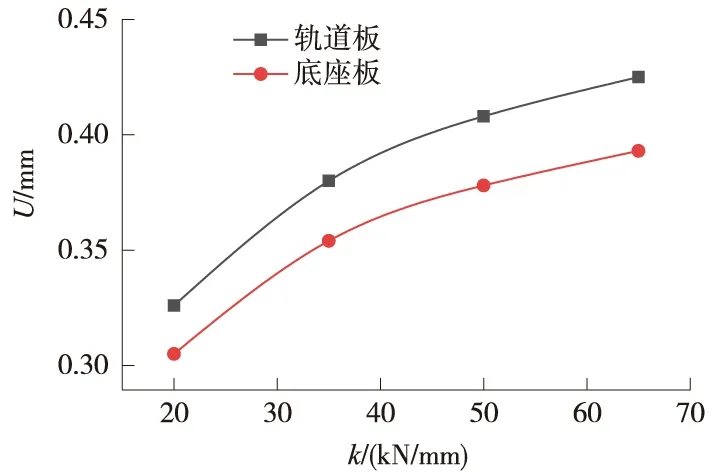
图8 竖向动位移峰值随扣件刚度的变化
4 路基病害造成的影响
若路基填料压实不足,密实度偏低,土体透水性增强,均会造成水分集聚和侵蚀路基,易使路基土软化产生不均匀沉降,在列车长期的疲劳荷载作用下,底座板不断拍打基床表层,会使路基结构的基床表层逐渐脱空而形成破坏[15-16]。
基床局部脱空通过ABAQUS软件中的model-change功能实现,在脱空面积为2.5 m×1.5 m不变的情况下,本节将模拟基床表层某个部位由完好情况到脱空深度不断增加的动力响应,共分为6种工况。
工况一,完好情况下(对照组);
工况二,脱空深度达2 cm;
工况三,脱空深度达4 cm;
工况四,脱空深度达6 cm;
工况五,脱空深度达8 cm;
工况六,脱空深度达10 cm。
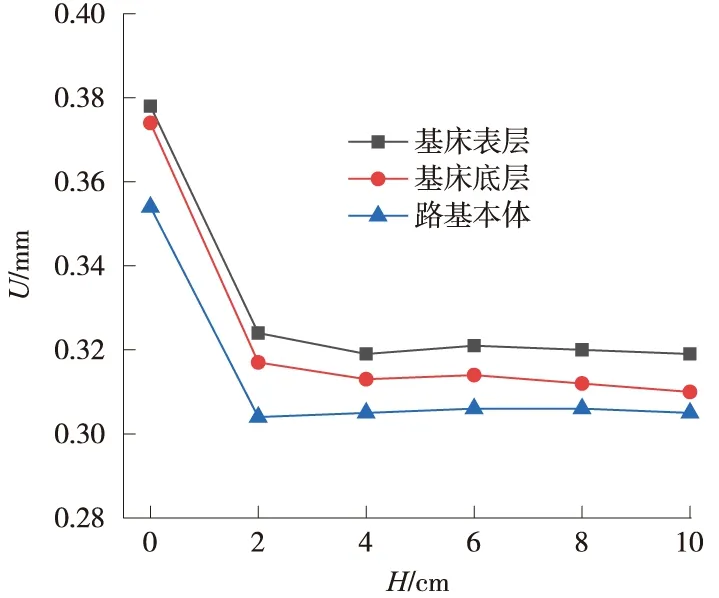
图9 竖向动位移峰值受基床局部脱空深度影响的变化
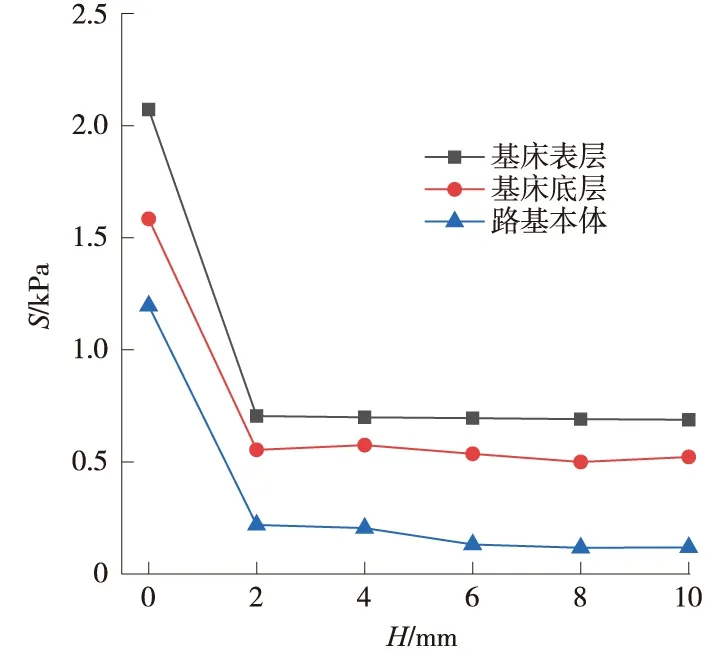
图10 竖向动应力峰值受基床局部脱空深度影响的变化
路基结构荷载作用点下方的竖向动位移峰值、竖向动应力峰值、竖向动加速度峰值如图9~图11所示。从图中可以看出,基床表层与底座板之间发生局部不接触时对路基结构的影响非常大,主要表现为脱空部位正下方的路基动力响应指标明显变小。工况一时,基床表层的竖向动位移、竖向动应力、竖向动加速度峰值分别为0.378 mm、2.07 kPa、10.07 m/s2;而在脱空后的工况六时,分别为0.319 mm、0.69 kPa、1.78 m/s2。降幅分别为15.6%、66.7%、82.3%。工况一基床表层的竖向动应力和加速度分别是工况六的3倍、5.6倍。
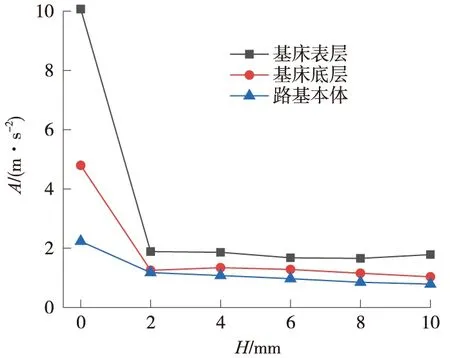
图11 竖向动加速度峰值受基床局部脱空深度影响的变化
工况一为未脱空状态,工况二~工况六为基床脱空状态,之所以脱空之后基床表层以下各指标值会比未脱空时小很多,是因为脱空之后基床表层与轨道结构不接触,原来本该脱空部分要受到的作用力由脱空区域边缘承担了绝大部分,使得基床表层以下受到的作用力大为减小。但是随着深度的增加,应力变化并不明显,这是因为上层轨道结构为钢筋混凝土结构强度较大,减弱了对下层路基结构的影响。当基床脱空的深度达到最大时(工况六),在基床脱空区域边缘读取点1、2、3、4、5、6、7、8的数据,点位选取见图12。

图12 点位选取示意
对比基床表层未脱空时荷载作用点下方的数据(点0),如表2所示。从表2可以看出,点0竖向动位移、竖向动应力、竖向动加速度峰值分别为0.378 mm、2.04 kPa、8.31 m/s2;而其他各点的最大竖向动位移、最大竖向动应力、最大竖向动加速度峰值分别为0.384 mm、2.85 kPa、9.05 m/s2,增幅分别为1.6%、39.4%、8.8%。竖向动应力的增幅明显,而竖向动位移、竖向动加速度的增幅不大,这说明脱空区域边缘承担了大部分动应力。

表2 基床局部脱空边缘数据与未脱空时荷载作用点下方数据对比
5 结论
建立高速铁路无砟轨道-路基-地基大系统,考虑CA砂浆层与土体材料的非线性属性,通过施加350 km/h的激振力荷载,模拟动荷载作用下轨道-路基系统的动力响应,分析列车车速、轴重、扣件刚度以及基床局部脱空对系统动力响应的影响,经过研究得到如下结论。
(1)动荷载对轨道结构影响较大,对路基结构影响较小。在轨道板上各扣件位置应力较大;在CA砂浆层中四个边角应力局部增大,易产生破坏;在路基结构中除中间轨道板对应位置应力较大之外,路基边坡也有不同程度的应力增大情况。
(2)车速对轨道-路基结构竖向动位移的影响并非简单的正相关关系,当速度从200 km/h增加到350 km/h时,轨道板竖向动位移峰值的增幅为16.9%;当车辆轴重从150 kN增加到220 kN时,轨道板竖向动位移峰值的增幅为28.4%;当扣件刚度从20 kN/mm增加到65 kN/mm时,轨道板竖向动位移峰值的增幅为30.3%。
(3)基床局部脱空对路基结构的影响较大,主要表现为脱空部位正下方的路基动力响应指标值明显变小。脱空区域边缘位置的竖向动应力增幅较大,当基床脱空深度达到最大时,脱空区域边缘的竖向动应力增幅最大达到39.4%。
