顾及相邻点变形关联性的GWO-LSTM变形预测模型
2021-12-27李浩标索广建郑旭东陈建营张献州
李浩标 索广建 郑旭东 陈建营 张献州
(1.西南交通大学地球科学与环境工程学院,成都 611756; 2.中国铁路上海局集团有限公司工电检测所,上海 200071)
1 概述
运营期高速铁路重点地段往往形变较大,科学分析和预测高速铁路重点地段的变形状况,能为高速铁路线路的高平顺性、高安全性提供重要保障[1]。在外界自然条件、时空效应等非线性因素的综合作用下,运营高速铁路重点地段变形监测数据通常为复杂的非平稳、非线性时间序列,利用历史变形监测数据准确预测未来一段时间的变形仍具有挑战性。
常用的高速铁路变形预测方法有回归分析、灰色理论、时间序列分析和人工神经网络等,厉东伟将BP神经网络应用于高速铁路沉降预测中,并达到所需预测效果[2];刘龙等将遗传算法优化BP神经网络模型用于高铁沉降评估,认为其预测效果优于标准BP神经网络[3];容静提出一种基于ARIMA与IGWO-SVM的沉降预测模型,发现模型优化后的预测性能大为提升[4]。然而,组合预测模型构建过程复杂,不利于实际推广使用。随着人工智能技术的迅速发展,长短期记忆(long short-term memory,LSTM)模型作为一种深度学习模型,具有十分强大的非线性拟合能力,可以挖掘出长短时间跨度下数据之间的关联性。王书芹基于LSTM模型利用历史数据预测未来瓦斯浓度[5];宋怡臻提出LSTM模型预测未来经济变化趋势[6];吉长东等利用LSTM模型实现未来GNSS卫星轨道预报[7]。虽然LSTM模型受到了广泛关注,但在运营高速铁路变形预测领域研究较少,具有一定研究价值。
LSTM模型网络超参数的选择直接决定其网络拓扑结构和网络预测性能,但需要进行多次实验,耗费时间精力较多。因此,决定采用具有全局收敛性的灰狼优化(Grey Wolf optimizer,GWO)算法进行超参数组合寻优。另外,传统变形预测模型中,没有考虑到监测点变形的关联性,应将监测点间的互扰性作为预测建模的影响因素。以某运营高速铁路重点地段沉降监测数据及仿真数据为例,构建顾及相邻点变形关联性的GWO-LSTM模型,并与BP模型进行对比,检验其适用性与精度。
2 LSTM模型与相邻监测点变形关联性分析
2.1 LSTM模型
循环神经网络(RNN)是一类以序列数据为输入,在序列的演进方向进行递归且按链式连接所有节点的递归神经网络,其优势在于考虑了序列数据的时序特征,即上一时刻的网络状态会对下一时刻网络状态产生的影响[8]。但是随着时序长度的增长,RNN在训练时容易出现梯度爆炸或梯度消失,影响网络输出的精度。因此,Hochreiter等对传统RNN递归神经网络进行改进,形成LSTM深度神经网络[9]。LSTM内部结构如图1所示,包含输入门、遗忘门、输出门和记忆单元等结构。3种门结构负责在神经网络的其他部分与记忆单元连接的边缘处设定权值,选择性记忆并反馈误差函数随梯度下降的修正参数[10]。记忆单元可以帮助LSTM减缓时序信息的损失速率,弥补RNN短期记忆、梯度爆炸等缺陷。
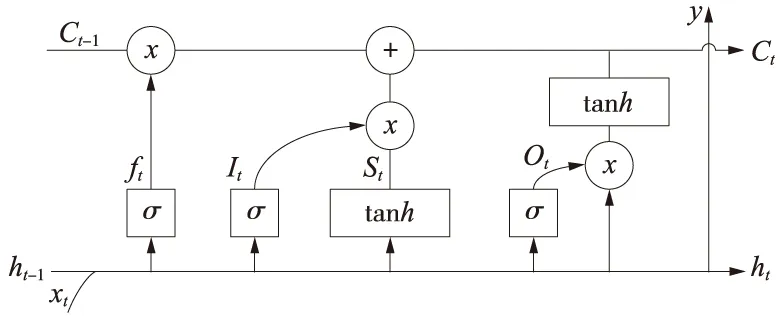
图1 LSTM内部结构
LSTM内部结构具体工作原理如下。
遗忘门是历史信息保留和遗忘的控制者,其计算见式(1)。它对前一时刻隐藏单元的输出ht-1与当前时刻的输入xt进行线性组合,并利用sigmoid激活函数,将其输出值变换到[0,1]之内,其中,1表示全部保留,0表示全部舍弃。
ft=σ(wfxxt+wfhht-1+bf)
(1)
式中,wfx、wfh分别为遗忘门接收信息的权重矩阵;bf为遗忘门的偏置项;σ一般为sigmoid激活函数。
输入门负责处理当前时刻信息的输入,控制输入数量,其具体计算过程为
It=σ(wixxt+wihht-1+bi)
(2)
式中,wix、wih分别为输入门接收信息的权重矩阵;bi为输入门的偏置项。
记忆单元负责综合当前时刻信息与过去记忆信息,当前单元状态会受到上一时刻单元状态的影响,其更新过程为
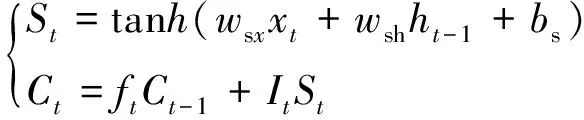
(3)
式中,wsx、wsh分别为记忆单元接收信息的权重矩阵;bs为记忆单元的偏置项。
输出门负责控制信息的输出,采用sigmoid函数对输出结果分类并用tanh函数进行记忆状态的变换,得到隐藏层传递给下一层的状态值ht,经过sigmoid计算得到当前时刻的输出值y,其计算见式(4)、式(5)。
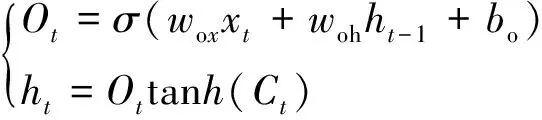
(4)
y=σ(wyhht)
(5)
式中,wox、woh分别为输出门接收信息的权重矩阵;bo为输出门的偏置项;wyh当前时刻隐藏层到最上层输出层的权重矩阵。
2.2 相邻监测点变形关联性
运营高速铁路重点地段变形监测网由多个变形监测点组成,每一个监测点的变化并不独立存在,既受其他监测点的影响,也会对其他监测点的变形产生影响。现有的变形预测模型多为单点预测模型,往往未考虑相邻点之间的变形影响,从而忽略了相邻点变形规律的整体关联性[11]。因此,除了考虑时间因素外,还考虑相邻点的变形关联性对变形的影响程度。可以利用Pearson相关系数衡量影响因素与监测点变形之间的相关程度,计算过程为

(6)
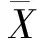
3 顾及相邻点变形关联性的GWO-LSTM模型
3.1 模型预测流程
建立顾及相邻点变形关联性的GWO-LSTM模型,其变形预测整体框架包括数据预处理、基于GWO的超参数优化、网络训练与网络预测,如图2所示。通过GWO算法对LSTM模型中的初始学习率、隐藏层单元数目两个网络参数在搜索空间优化,确定最佳参数组合。将某时刻监测点的变形值与影响特征作为输入数据,将下一时刻监测点变形预测值作为输出数据,通过LSTM迭代自适应调整权重拟合形成GWO-LSTM模型。最后,把测试数据输入训练网络进行预测,将预测结果与真实值进行误差对比并输出。
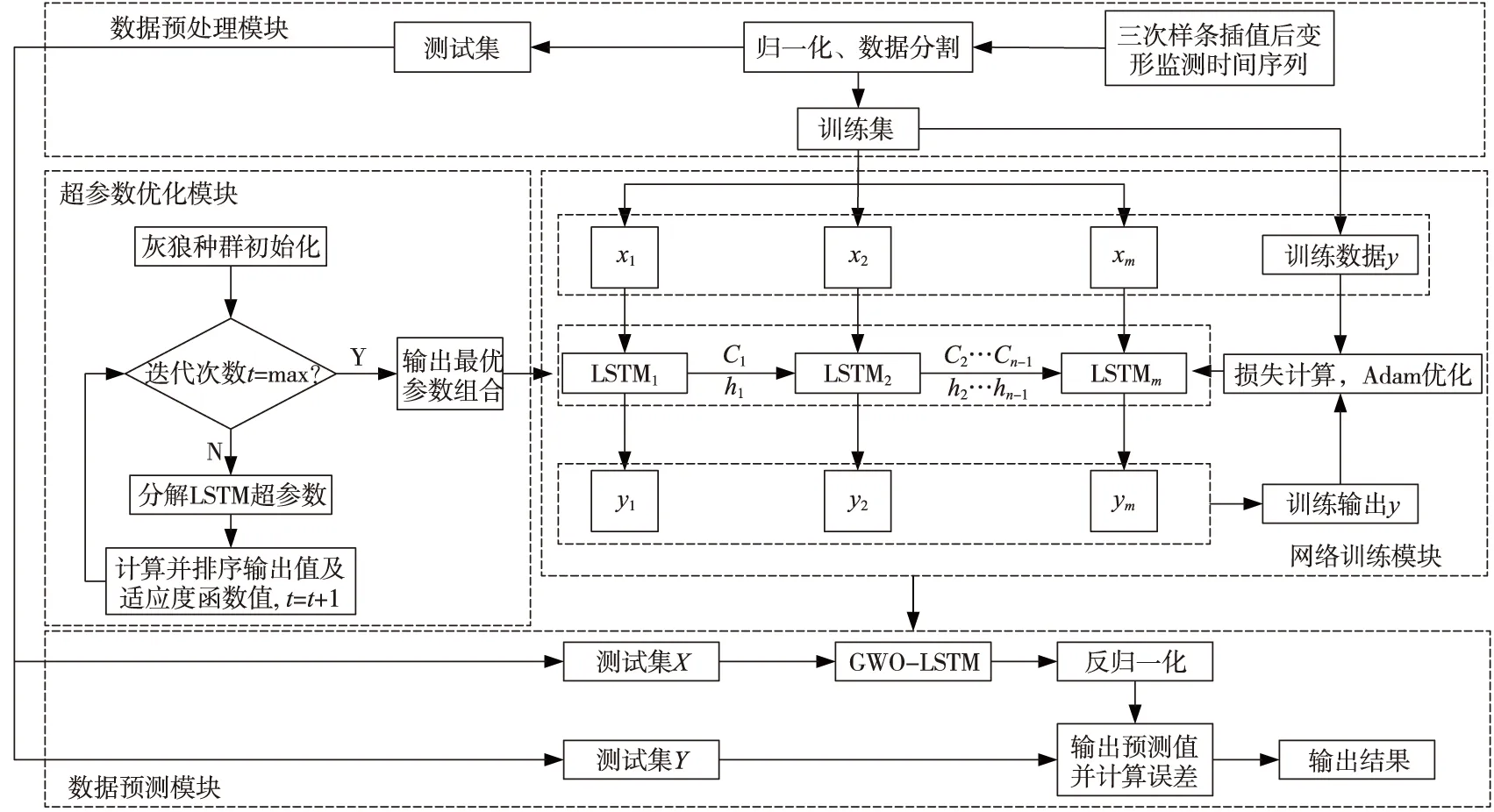
图2 GWO-LSTM模型变形预测整体框架
3.2 数据预处理
运营高速铁路重点地段变形监测为周期性监测,其周期根据变形速率和评判标准动态调整[12]。受天窗时间、天气状况等条件限制,实际监测无法按照等间隔周期进行。根据时间序列预测对监测数据的要求,选用3次样条插值函数将非等间隔监测数据转化为等间隔监测[13],其函数原理如下。
设区间[a,b]上有n+1个样本点(xi,yi)(i=0,1,…,n),函数S(x)在整个区间[a,b]为二次连续可微函数,在每个子区间[xk-1,xk](k=1,2,…,n)是一个不超过三次的多项式,在每一个结点上满足S(xi)=yi(i=0,1,…,n),则称S(x)为三次样条插值函数。
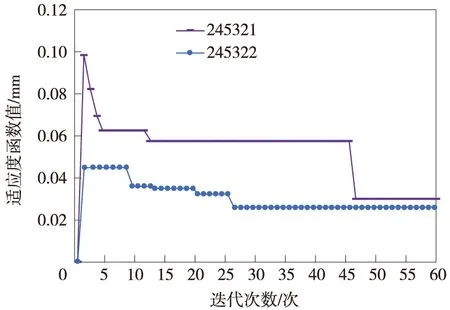
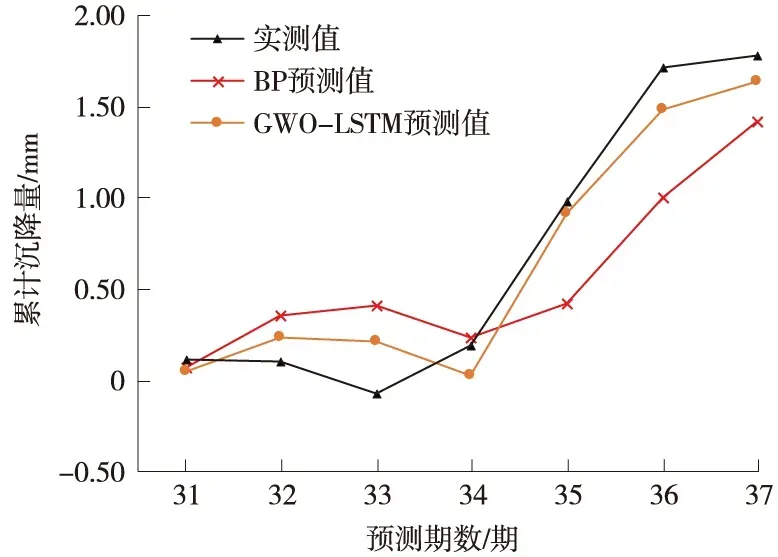
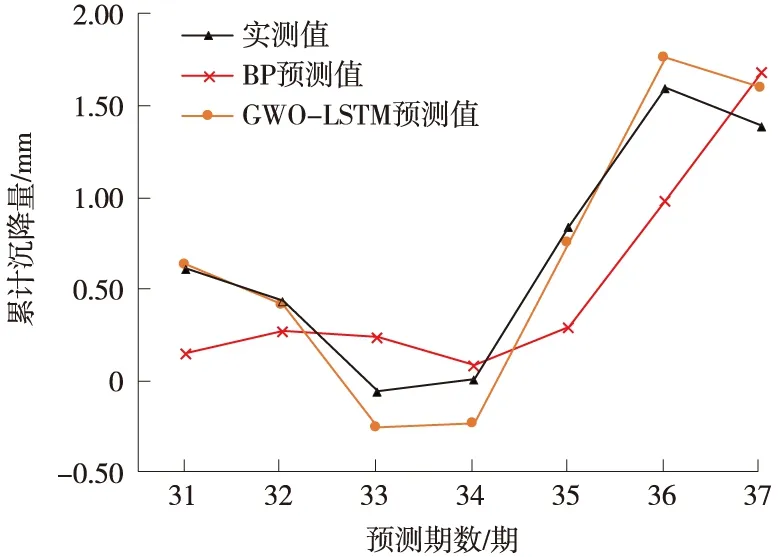
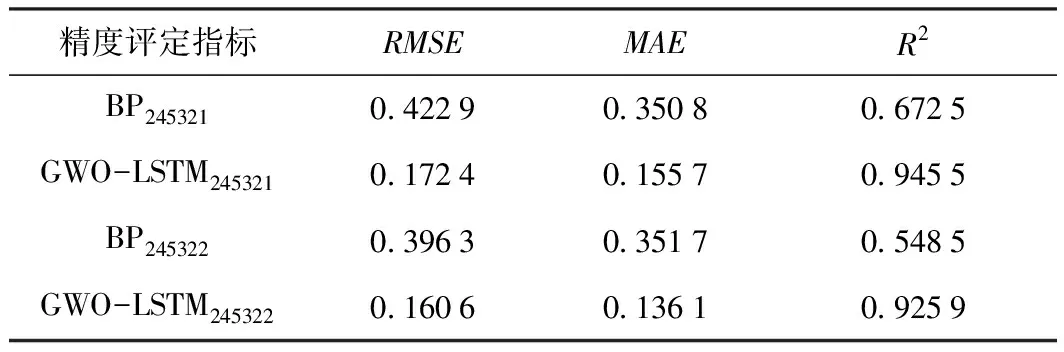
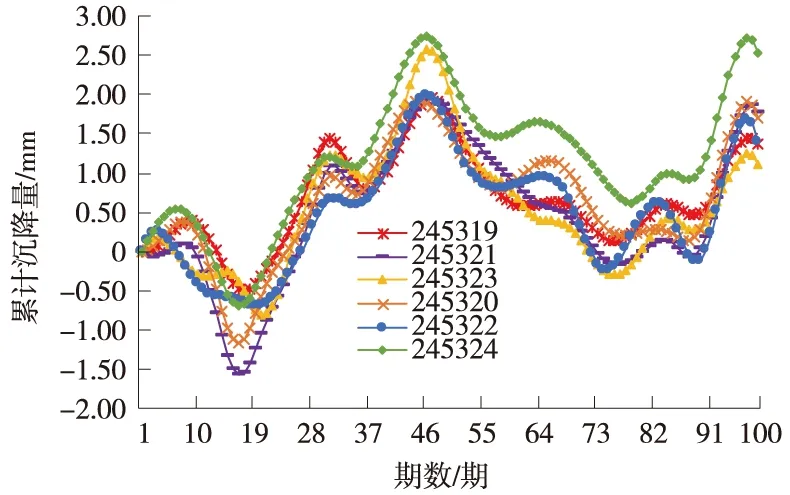
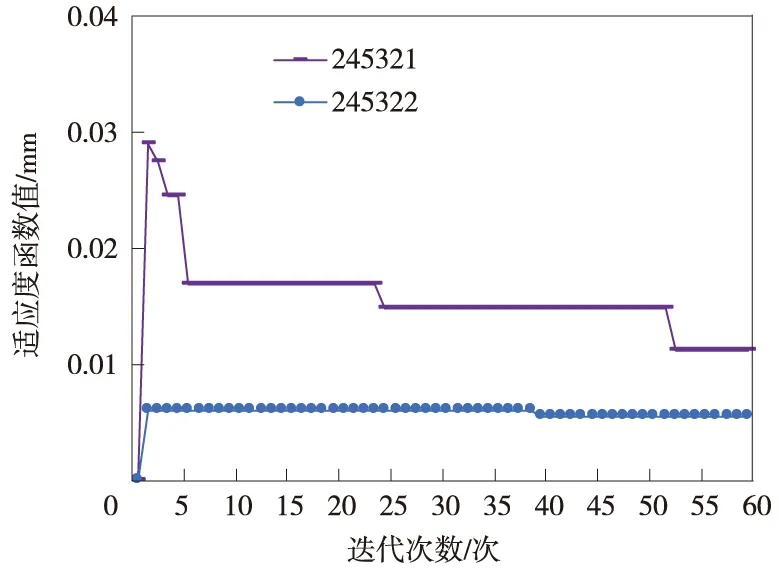
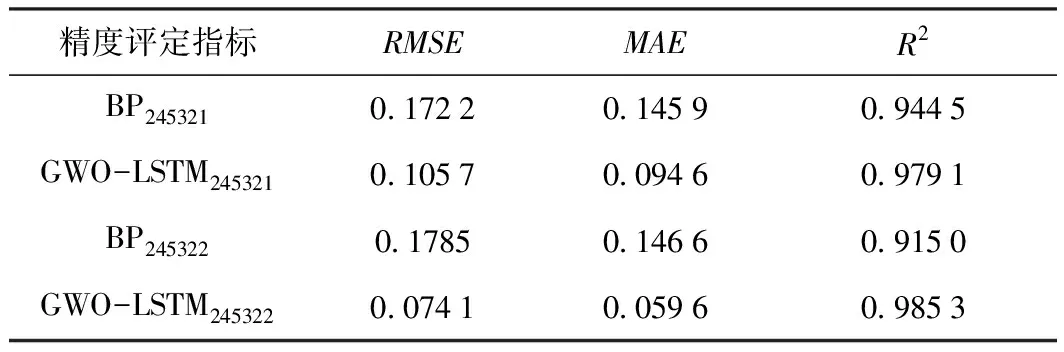
将变形监测数据输入于预测模型前,需要将其划分为训练集ttr=[x1,x2,…,xm]和测试集tte=[xm+1,xm+2,…,xn],其中限制条件为m (7) 式中,x是变形监测数据;y是归一化后的结果;xmin和xmax分别是变形监测数据中的最小值和最大值。 LSTM模型预测性能取决于网络超参数的选择,主要的网络超参数有初始学习率、隐藏层单元数目等,但目前没有通用方法,多采用经验法确定[14]。已有许多学者开展相关研究,许宁提出采用多层网格搜索法,以一种网格遍历的方式依次尝试每种超参数组合[15]。多层网格搜索法虽然有不错的寻优能力,但存在容易陷入局部最优、匹配完所有组合才能结束搜寻导致的效率低下等诸多缺陷,故在实际应用中,一旦超参数个数增多,遍历所有的参数组合将耗费大量时间,故该方法还不是一种非常智能的方法。针对以LSTM为基础建立的运营高速铁路变形预测模型,所涉超参数较多且搜索空间范围较大,为提高超参数寻优的精度和效率,决定引入GWO算法进行超参数组合优化。 GWO算法源于生物界,是一类对灰狼的狩猎行为与社会等级层次进行模仿的新型群体智能优化算法,其优势为全局收敛性好、参数少、易实现等[16]。在灰狼种群中,灰狼按等级划分为α、β、δ及ω。每一个灰狼对应着一组超参数,即α、β、δ及ω分别为最优解、次优解、第三优解与候选解[17]。使用GWO算法对LSTM模型最优参数组合搜寻,其主要步骤如下。 (1)确定超参数取值范围,初始化灰狼种群,确认灰狼个体的位置向量。 (2)将预测结果的均方根误差RMSE作为适应度函数,学习训练样本计算出灰狼的适应度值并进行灰狼种群等级划分。 (3)根据式(8)~式(13),对灰狼个体信息进行位置更新,将位置更新后的适应度函数值与上一代的进行比较,保留最优适应度函数值和最优参数,直至迭代次数满足,搜索到全局最优参数组合,否则返回第(2)步继续迭代。 (8) Bk=2r1,k=1,2,3 (9) (10) (11) Ak=2ar2-a,k=1,2,3 (12) a=2-t/tmax (13) LSTM模型与传统神经网络模型相同,可以有多个隐藏层,单隐含层可以通过调节隐藏层单元数目来实现和多隐藏层几乎一样的效果[18],故采用单隐藏层LSTM模型。LSTM模型训练时,采用GWO算法选定的最优参数组合,将训练集ttr中影响特征与监测点变形值输入于网络输入层,经前向传播由全连接层回归分析得出训练集ttr中下一时刻变形值,通过损失函数计算偏差,其损失函数采用均方误差MSE。若超过预期值,需要通过BPTT算法反向传播修正连接权重并采用自适应Adam优化算法调节网络梯度[19],进而得出LSTM训练的全局最优解。 运营高速铁路变形预测中,可采用单步预测与多步预测,预测方式又可分为直接多步预测、基于多输入多输出策略(MIMO)的多步预测、递归多步预测和随时间推进的单步预测等[20]。对于直接多步预测和基于多输入多输出策略的多步预测,两种方法虽然都建立每个时间步与当前状态的联系,但具有模型构造复杂与训练困难等缺陷。递归多步预测与随时间推进的单步预测都直接利用训练好的单步预测模型,不需要额外训练,其区别在于预测阶段时间有没有推进[21]。进行递归多步预测时,停留于时刻i,将预测值当作真实值加入历史序列不断递归预测下一时间步序列值,但这样会产生误差累积效应。随时间推进的单步预测是指随时间推进将真实值加入历史序列不断往前扩展递归预测,即在时刻i预测时刻i+1,等到了i+1,知道真实值再预测时刻i+2,以此类推。其模型容易实现,预测精度取决于训练好的网络。综合实际应用考虑,选用随时间推进的单步预测进行研究。 预测时,首先将测试集tte中影响特征与监测点变形值输入训练好的网络中,即可得到对应的预测值,然后需要进行反归一化处理,其函数关系见式(14),并与真实值进行对比,求出预测模型精度。 x=y·(xmax-xmin)+xmin (14) 式中,x是反归一化后结果;y是预测值;xmin和xmax分别是变形监测数据中的最小值和最大值。 运营高速铁路变形预测模型性能指标较多,采用RMSE、MAE和确定系数(R2)作为模型的评估指标,如式(15)~式(17)所示。预测模型RMSE和MAE越小,则预测精度越高;R2越大,则预测值与真实值相关程度越高。 (15) (16) (17) 某运营高速铁路位于华东平原地区,与多条重要高铁相接,作为我国“八纵八横”高铁客运网主要通道之一。其中,K0245+002~K0246+044为无砟轨道路桥过渡段,受温度等外界条件与时空效应因素影响发生变形,故将其列为重点沉降监测地段。从2017年5月25日到2018年11月16日,在该地段共完成37期监测,监测频率原则上规定为1次/15 d,但受天窗期与天气的影响无法严格执行。其沉降监测纵断面分为上下行路肩断面、上下行底座板外侧断面、上下行轨道板断面,横断面每50~70 m布设1个,路肩CPⅢ点位布设如图3所示。 图3 CPⅢ点位布设 以变形较为严重的CPⅢ点245321与245322为例,分别对该点与其相邻的CPⅢ点进行三次样条插值处理,插值后累计沉降变化如图4所示。通过Pearson相关系数法确定两点的影响特征,如表1与表2所示。结果表明其相关系数均大于0.6,下一时刻的变形与上一时刻各点的变形存在强相关性。因此,分别选用245319、245321与245323的上一期沉降量作为245321下一期沉降量的影响特征,选用245320、245322与245324的上一期沉降量作为245322的影响特征,将构建输入向量维度为3,输出向量维度为1的GWO-LSTM模型进行预测,可获得36组样本数据,将前29组数据作为训练集,后7组作为测试集,即预测期次为31~37期。 图4 三次样条插值后监测点累计沉降变化 表1 245321相关性分析 表2 245322相关性分析 采用GWO算法对LSTM模型中初始学习率与隐藏层单元数两个参数进行优化。设置灰狼个体数为30,迭代次数为60,初始学习率与隐藏层单元数的搜索空间分别为0.001~0.9和1~30,LSTM模型中训练轮数为100,梯度阈值为1,学习率下降因子为0.2。经过优化,随着迭代次数的递增,GWO-LSTM模型可以在搜索空间中快速找到近似最优解,245321与245322的适应度函数值曲线如图5所示,所搜寻到的最优超参数如表3所示,并将其代入模型中进行网络训练预测。 图5 适应度函数曲线 表3 最优超参数 为分析GWO-LSTM模型的拟合预测性能,建立BP模型与之进行比较,两种方法对245321与245322的预测结果如图6与图7所示,预测精度见表4。可以看出,不论对于245321还是245322,两个模型都能对其变化趋势进行一定程度的拟合预测,该地段除了受时空效应影响,还受温度、风速、荷载等环境因素影响,故所建立的模型不可避免地与实测值有一定程度的偏离。其中BP模型预测趋势偏离实测值较大,而GWO-LSTM模型预测趋势更接近实测值,表现出优于BP模型的预测精度。 图6 245321预测结果对比 图7 245322预测结果对比 表4 模型精度评定对比 为进一步验证GWO-LSTM模型的拟合预测性能,通过3次样条插值函数,将监测频次为1次/15d的37期监测数据转换为监测频次为1次/5d的109期监测数据,模拟其变形趋势如图8所示。与之前同样的预测方式,可获得108组数据,前89组数据作为训练集,后19组作为测试集,分别对245321与245322的91~109期进行仿真实验预测。 图8 109期监测点累计沉降变化 在其余参数不变的条件下,随着迭代次数的递增,245321与245322的适应度函数值最终趋于收敛,曲线如图9所示。所搜索到的最优超参数如表5所示,并将其代入模型中进行网络训练预测。 图9 适应度函数曲线 表5 最优超参数 对于三次样条函数模拟出的245321与245322,GWO-LSTM模型与BP模型的预测结果如图10、图11所示,预测精度见表6。分析可知,GWO-LSTM模型的拟合预测曲线较BP模型更贴近真实曲线,进一步证明了GWO-LSTM模型对非线性数据的拟合预测能力强于BP模型。此外,结果也说明了建模时除了考虑影响特征因素外,还可以提高监测频次来减少预测数据的离散性,进而获取更好的预测效果,这为未来运营高速铁路自动化变形监测大数据预测分析打下了基础。 图10 245321预测结果对比 表6 模型精度评定对比 以某运营高速铁路重点地段沉降监测数据及仿真数据为例,建立顾及相邻点变形关联性的GWO-LSTM模型进行处理分析,得出以下结论。 (1)运营高速铁路沉降变形是综合影响因素作用下的结果,其预测建模不仅需要考虑外界环境的影响,还需要从时空角度上考虑相邻监测点变形的空间关联性。 (2)相较于以往的经验试凑法,GWO算法可以快速实现LSTM模型的超参数寻优,提高变形识别与预测效率。 (3)相较于BP模型,GWO-LSTM模型更适合应用于运营高速铁路沉降变形分析预测。 (4)虽然可以用GWO-LSTM模型实现单一监测点未来短期分析预测,但只针对于单一监测方式的数据,全线多源数据同步分析预测是以后研究的方向。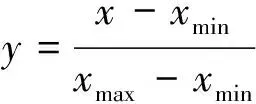
3.3 基于GWO的超参数优化
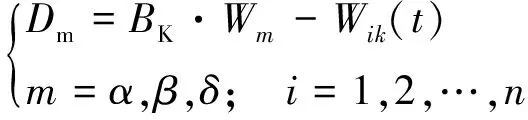
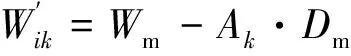

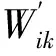
3.4 网络训练
3.5 网络预测
3.6 预测性能指标
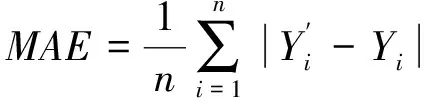

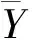
4 实例应用
4.1 工程概况

4.2 数据预处理



4.3 GWO训练寻优

4.4 预测结果分析
5 仿真实验
5.1 仿真实验验证

5.2 仿真实验结果分析

6 结论
