带钢短柱UHPC夹芯板抗弯性能试验研究与有限元分析

李 卫, 晏班夫, 邵旭东, 余加勇

(1.湖南大学 风工程与桥梁工程湖南省重点实验室， 湖南 长沙 410082; 2.中交公路规划设计院有限公司， 北京 100088)

UHPC(超高性能混凝土)夹芯板是一种以水泥、细砂、硅灰、高效减水剂、钢(耐碱玻璃纤维)等为主要原料的新型夹芯板结构，具有结构质量轻、传热能力差、耐久性优势明显等诸多优点。UHPC由于其特殊的原料具有以下力学性能优势：超高强度、超低吸水率、超强耐久性和耐侵蚀性能[1-2]。目前，UHPC多用于公路桥梁，海洋工程、建筑工程、结构加固维修等。

针对普通混凝土夹芯板抗弯性能方面的研究较多。例如，李砚波[3]等对普通混凝土夹芯板进行了抗弯试验研究，并对相关规范中的受弯构件计算公式进行了补充。俞剑勇[4]等建立了CS板的非线性有限元计算模型，分析了CS板结构几何条件的变化对CS板力学性能的影响。而就目前来说，对于UHPC夹芯板抗弯性能的研究还很少。因此对UHPC夹芯板进行研究以获得其力学性能就显得尤为重要。

本文设计并制作了2片UHPC夹芯板，并同时结合静力试验与有限元分析2种方法对其力学性能进行了研究。研究中验证了不同夹芯板的极限承载力及破坏模式，在验证有限元模型准确可信的前提下，对模型进行了参数分析，掌握了底板主筋配筋率、顶底板厚度、板高度以及短柱尺寸对UHPC夹芯板抗弯性能的影响规律。

1 模型试验

1.1 试验板设计

试验共制作了2块夹芯板，顶底板的厚度均为5 cm，宽度40 cm，夹芯板总的高度为25 cm，夹芯板层的厚度为15 cm。为了方便叙述，在此分别将2块板定义为SP1与SP2，其中试件SP1的长度为240 cm，不锈钢短柱高25 cm，外径6 cm，壁厚为0.5 cm，短柱的横向间距为20 cm，纵向间距20 cm；试件SP2的长度为260 cm，不锈钢短柱高25 cm，外径4.8 cm，壁厚为0.3 cm，短柱的横向间距为20 cm，纵向间距30 cm。其中顶底板受力钢筋直径分别为8 mm和14 mm，间距为10 cm；顶底板内采用直径为6 mm的分布钢筋来固定受力钢筋的位置，其间距为对应不锈钢短柱的纵向距离。各试验板的主要设计参数如表1所示，试验板立面图如图1所示，试验板配筋图如图2所示。

表1 试验板设计主要参数Table 1 Main parameters of test board design试件编号l0bhλ短柱尺寸顶板纵筋底板纵筋SP124040253.26-0.53A8@103C14@10SP226040253.64.8-0.33A8@103C14@10注:表中除钢筋直径单位为mm,其余单位均为cm。

(a) SP1板

图2 试验板配筋图(SP1、SP2)(单位:mm)

1.2 UHPC力学性能

顶底板UHPC以及短柱中内填UHPC均为同种材料，对材性试块与试验模型进行同步养护，在正式加载前进行材料性能测试，测试结果如下：立方体抗压强度161 MPa,棱柱体抗折强度25.2 MPa,弹性模量Ec为48.6 ×104MPa。

1.3 测试内容及加载模式

本试验采用4点加载方案，剪跨比均大于3，模型均采用简支支撑。为了保证模型边界约束的可靠性，在试验模型的一侧采用固定铰支座，另一侧采用滚动支座。各试验板的纯弯段均为60 cm，试件SP1剪跨段长80 cm，试件SP2剪跨段长90 cm。在板顶底表面的纯弯段内3个截面上布有混凝土应变片，对应顶底板侧面同一位置也布有混凝土应变片，在支座处顶板附近用千分表测量支座处的挠度，沿板长加载点以及跨中3个位置点处布置有百分表用来测量板的挠度，同时为了测量顶底板水平方向的滑移，在短柱与顶底板交汇处的剪跨段板侧喷有散斑点，散斑点的具体位置如图3所示，现场试验相机位置如图4所示。

图3 散斑点区域示意图Figure 3 Schematic diagram of scattered spots

图4 相机布置图Figure 4 Camera layout

试验过程中，应变数据用静态数据采集仪采集。加载装置为100 t手摇油压千斤顶，荷载由压力传感器测量。裂缝宽度采用裂缝宽度观测仪进行量测，其测量的精度为0.01 mm。现场试验加载装置如图5所示，试验加载方式以及测点位置如图6所示。

图5 试验现场加载装置图Figure 5 Test site loading device diagram

图6 试验加载及测点布置Figure 6 Test loading and layout of measuring points

1.4 试验加载制度

在正式加载之前，首先对试件进行预加载，预加载的目的是为了检查仪器设备是否完好，预加载结束后正常卸载，之后开始正式加载。

正式加载时采用分级加载，每级荷载大约为预计极限荷载的5%，待加载到预估开裂荷载时减小荷载步。等试件开裂后，仍按照原先的荷载步进行加载，每级荷载持续5 min左右，待达到破坏荷载的80%时，减少荷载步，直至试件破坏。每级荷载稳定后记录相关数据。

2 试验结果及分析

2.1 荷载-位移曲线

各试件荷载位移曲线如图7所示，由于试件的剪跨段长度不同，因此将纵坐标荷载转换成对应板跨中弯矩。各试件主要试验结果见表2。图7中可以看出各试件整个试验加载过程，试件SP1与试件SP2有着较为明显的区别。

图7 荷载-跨中挠度曲线Figure 7 Load-Mid-span Deflection Curves

表2 试验板主要结果汇总Table 2 Summary of main results of test panel试件编号破坏荷载/(kN·m)初裂荷载/(kN·m)破坏形态SP195.134.8底板弯曲破坏SP261.314.3挠度过大

由图7可知，试件在加载破坏过程中均经历以下3个阶段，即线弹性阶段、裂缝发展阶段、屈服破坏阶段。在线弹性阶段，试件均未出现裂缝，荷载与挠度呈线性关系，试件的刚度几乎保持不变，但二者在弹性阶段的刚度略有差异；当裂缝开始处于发展趋势后，截面刚度均有不同程度降低，在该阶段很长的一段加载时间内，UHPC底板出现不同程度的开裂，裂缝的数量、裂缝的宽度和长度不断扩展，同时也有部分细小的裂缝出现，该阶段持续至底板钢筋屈服；在钢筋屈服后，试件挠度增长较快，经历很短的屈服强化阶段后各试件进入破坏阶段。

相较于试件SP1，试件SP2在裂缝出现后刚度下降较为明显，挠度增长更快，同时试件SP2在裂缝发展阶段曲线较为平缓，而试件SP1在进入持荷破坏阶段时有明显的拐点。这与试件的裂缝分布有着很大的关联，试件SP1主裂缝集中在底板跨中区域，裂缝分布较密集，在钢筋屈服之前试件能够维持较高的刚度，钢筋屈服后试件刚度下降明显。试件SP2由于其裂缝分布的较为分散，裂缝分布于剪跨段短柱附近的底板处，试件刚度随着裂缝离散增加而缓慢下降，导致曲线在该阶段较为平缓。各试件在加载后期，底板钢筋均屈服，试件SP1的裂缝宽度不断增加，随着钢纤维拔出的“噼啪”声，荷载不增反降，试件迅速进入破坏阶段；试件SP2未出现钢纤维拔出的“噼啪”声，荷载缓慢增加，挠度增长迅速，最终试件因为挠度过大而无法承载。

2.2 荷载-滑移曲线

各试件在弹性阶段的滑移分布曲线如图8所示。

从滑移的分布曲线可以看出，板跨中滑移量几乎为0，从跨中向支座两侧滑移量逐渐增加，试件SP1的最大滑移量为0.05 mm，试件SP2的最大滑移量为0.09 mm，这是因为试件SP1的短柱直径较大，短柱的纵向间距较小，板的抗滑移刚度较大，整体性能较强，试件的滑移量较小。

2.3 破坏形态

SP1板最终破坏形态如图9(a)所示，可以看出最终破坏时底板纯弯段有一条非常明显的主裂缝和少数密集次裂缝，裂缝最大宽度超过1 cm，试件顶板上缘未被压碎，但底板钢筋已经屈服。在加载后期时，底板钢筋屈服后纯弯段裂缝宽度急剧增长，底板主裂缝处钢纤维被拔出，试件不能继续承载。

SP2板最终破坏形态如图9(b)所示，其破坏形态为剪跨段短柱附近的UHPC密集开裂，整体来看裂缝分布较为分散，主裂缝不明显，位于加载点附近的顶板UHPC有轻微压碎现象，底板钢筋屈服。在试验后期，虽然荷载能够保持稳定，但跨中挠度持续增大，试件最终因挠度过大而无法继续承载。

2.4 试验结果分析

综合上述试验结果，可做出以下分析。

a.试件SP1由于其短柱直径较大，分布较密，试件在承载力、抗裂性能、刚度等受弯性能均优于试件SP2，但试件SP2延性更好。

b.试件SP1与试件SP2破坏形态及裂缝发展说明，短柱直径大小，分布的密集程度主要会影响试件的抗滑移刚度，从而影响试件的整体复合程度，影响试件的裂缝发展过程以及破坏形态。试件的抗滑移刚度越大，试件的整体性能就越强，试件的裂缝分布以及破坏形态更加接近普通混凝土板受弯破坏；当试件的抗滑移刚度较小时，试件的整体性能低，短柱处的集中应力越明显，裂缝分布也会比较分散。

3 有限元模型建立

为了研究带钢短柱UHPC夹芯板4点抗弯试验的全过程，通过有限元分析软件ABAQUS建立模型，采用分离式建模方式对上述2块夹芯板试件进行数值模拟。其中为了避免加载点以及支座处出现应力集中现象，在模型中顶底板的相应区域建立钢块与面板绑定。

3.1 单元类型

本文中的UHPC、钢块、不锈钢短柱均采用实体单元C3D8R来模拟，钢筋采用桁架单元T3D2模拟。

3.2 材料本构模型

对于混凝土抗弯试件在单调荷载的作用下，聂建国[6]等通过研究发现塑性损伤模型能够模拟得更加准确，模拟结果与试验更加接近。同时该模型能够分别考虑材料的受拉与受压性能，其主要失效原理是材料的受拉开裂破坏以及受压压碎破坏[7-8]。因此本文中的UHPC采用混凝土损伤塑性(CDP)模型，模型中的其他参数如下： 膨胀角30°，偏心率0.1，双轴极限抗压/单轴极限抗压1.16不变应比为0.666 7，粘性系数0.001。

受压本构采用文献[9]中提出的相应的UHPC受压本构关系式，即:

(1)

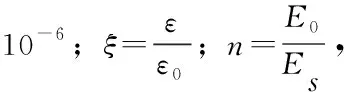
受拉本构采用文献[10]中提出的UHPC受拉本构关系式，即:

(2)

式中：fct为应变硬化阶段平均应力，取8 MPa；εca为线性拐点处的应变，取εca=199×10-6;εpc为最大应变，取1 914×10-6。

最终通过公式计算、数据整理得到UHPC拉压本构关系曲线，如图10所示。

图10 UHPC本构关系曲线Figure 10 Constitutive relationship curve of UHPC

钢筋的本构模型如图11所示，钢筋型号为HRB400，参考相关文献取屈服强度fy=482 MPa；弹性模量Es=200 GPa；泊松比μ=0.3。

图11 钢筋本构关系曲线Figure 11 Constitutive relationship curve of Reinforcement

由于不锈钢材料的特殊性，其本构模型中的屈服点不显著，通常用塑性应变为0.2%对应的应力作为其屈服强度，本文参考文献[11-12]得到不锈钢的力学性能为E0=200 GPa；σ0.2=230 MPa；σu=540 MPa，对应的本构关系式为：

(3)

最终通过公式计算、数据整理得到不锈钢材料的本构关系曲线，如图12所示。

图12 不锈钢本构关系曲线Figure 12 Constitutive relationship curve of stainless steel

3.3 相互作用定义

在模型中存在不锈钢短柱与UHPC、钢筋与UHPC以及支座、垫块与UHPC之间的相互作用。

不锈钢短柱埋在UHPC面板内的那一部分与UHPC约束关系采用嵌入(Embedded)。

钢筋与UHPC的约束关系采用嵌入(Embedded)约束。

支座与UHPC面板、垫块与UHPC面板采用绑定(Tie)约束，该约束能够使得模型中的两部分不产生相对运动。

3.4 计算结果对比分析

将有限元分析得到的试件荷载跨中挠度、滑移分布曲线、破坏形态等结果与试验值进行比较，检验有限元计算的合理性，为后续参数分析提供支持打下基础。

3.4.1荷载-跨中挠度曲线

图13中的对比曲线可以看出，2条曲线吻合得较好且趋势基本能够保持一致。各曲线均存在2个较明显的拐点，图中A、B两点，其中A点为板的开裂点，B为钢筋屈服点。在A点之前的弹性阶段，荷载与跨中挠度呈线性关系，有限元计算值与试验值几乎保持一致。在A点以后的裂缝发展阶段，曲线出现了不同程度的偏差，主要原因是试验加载过程中存在偏载的可能，板体倾向于先开裂一侧，导致百分表在测量位移数据时发生不垂直的位移变化；再有就是有限元模拟的材料本构、边界条件与实际情况存在偏差。B点以后的屈服破坏阶段，试件的刚度下降明显直到试件完全破坏。将A、B两点的试验值与有限元计算值汇总于表3。总的来说，两条曲线偏差不多吻合较好，这也说明了通过有限元模拟分析的可靠性。

图13 荷载-跨中挠度曲线对比Figure 13 Comparison of load-span deflection curves

表3 转折点处弯矩对比分析结果Table 3 Comparative analysis of bending moments at turning points试件弯矩(A)/(kN·m)弯矩(B)/(kN·m)试验值计算值相对误差/%试验值计算值相对误差/%SP1板34.832.95.495.190.35.0SP2板14.315.69.161.356.28.3

3.4.2滑移分布曲线

图14为试件开裂荷载时顶底板的滑移分布曲线对比图，可以看出曲线吻合得较好。从有限元计算的结果可以看出，滑移沿着板的纵向严格对称分布，跨中顶底板滑移为0，位于支座处的滑移量最大，与试验测量结果保持一致。说明有限元模拟分析具有一定的可靠性。

图14 弹性阶段顶底板滑移分布曲线Figure 14 Top-bottom slip distribution curve in elastic stage

3.4.3裂缝形态分布图

图15为各试件在达到极限承载力时的等效塑性应变图，该图可以很好地反映试件的裂缝形态以及对应的位置布置，从计算结果可以看出，试件SP1破坏时最终裂缝分布主要集中在底板跨中区域，试件SP2破坏时最终裂缝分布主要集中在顶板加载点处以及剪跨段底板短柱附近。对比试验最终破坏形态图9可以看出，二者在裂缝分布位置以及形态均吻合得较好。

(a)SP1板

4 参数分析

4.1 参数确定

在验证了有限元模拟分析的可靠性以后，采用有限元对试件进行参数分析，从而进一步揭示带钢短柱UHPC夹芯板的力学性能。在试件SP1的基础上，研究底板纵筋配筋率，顶底板的厚度、板的高度以及不锈钢短柱的尺寸对试件抗弯性能的影响。具体参数见表4。

表4 参数汇总Table 4 Summary of parameters试件编号底板钢筋直径/mm顶板高度/cm底板高度/cm板高度/cm(短柱直径-壁厚)/(mm-mm)SP114552560-5SP316552560-5SP412552560-5SP514442560-5SP614452560-5SP714342560-5SP814551560-5SP914552060-5SP1014442060-5SP1114552548-3SP1214552542-3

4.2 结果对比

根据有限元的计算，提取了每个分析结果中的荷载-跨中挠度曲线，为了便于与前文统一，这里的荷载仍然取对应板中的跨中弯矩。如图16所示为每个试件的荷载-挠度曲线，模型中计算得到的开裂荷载以及极限荷载如表5所示。

(a)不同配筋率

表5 有限元计算结果汇总Table 5 Summary of finite element calculation results试件编号开裂荷载/(kN·m)极限荷载/(kN·m)SP1 32.990.3SP3 31.6103.6SP4 31.080.6SP5 24.078.8SP6 27.888.0SP7 20.372.1SP8 16.852.3SP9 25.873.0SP1020.465.0SP1120.864.3SP1216.753.0

4.2.1配筋率

图16(a)为不同配筋率模型的荷载-跨中挠度曲线，可以发现，当底板纵筋配筋率提高时，有限元模型开裂荷载几乎保持不变，说明纵筋配筋的改变对板开裂前的抗弯性能影响较小；开裂以后板的刚度随着配筋率的提高而提高，继而板的极限承载力也有一定程度的提高。

4.2.2顶底板厚度

图16(b)为不同顶底板厚度模型的荷载-跨中挠度曲线，可以看出，随着顶底板厚度的增加，试件的开裂荷载以及极限荷载均有所增加，但增幅不尽相同，相较于顶板厚度，底板厚度对开裂荷载及极限荷载的影响更加显著。板的高度越高，顶底板厚度的改变对开裂荷载及极限荷载影响越大。

4.2.3板高度

图16(c)为不同板高模型的荷载-跨中挠度曲线，从中可以看出，板高度的变化对试件开裂荷载和极限荷载的影响是显著的，随着板的高度的降低，对应试件开裂荷载、极限荷载以及开裂后板的刚度均降幅明显，且板高度越低，对应的降幅越明显。

4.2.4短柱尺寸

图16(d)为不同短柱模型的荷载-跨中挠度曲线，短柱的直径减小时，试件对应的开裂荷载与极限荷载同样下降明显。与改变板高度不同的是，改变短柱直径是通过改变顶底板抗滑移刚度间接影响板的抗弯刚度，从而影响板的抗弯性能。

综上所述可以看出，板的高度和不锈钢短柱的直径是影响板受力性能最重要的因素，其次是顶底板的厚度和底板钢筋的配筋率，其中顶底板厚度对板抗弯性能的影响程度与板的高度有关，当板的高度较低时，顶底板厚度的影响程度更加明显；而底板钢筋的配筋率对试件的开裂荷载影响不大，对试件开裂后的抗弯性能有一定影响。

5 结论

本文结合带钢短柱UHPC夹芯板抗弯性能试验结果以及有限元软件ABAQUS的模拟分析，得出了如下结论：

a.在荷载作用下UHPC夹芯板的破坏全过程可以分为3个阶段，分别是线弹性阶段、裂缝开展阶段以及屈服破坏阶段。

b.当板的高度相同时，短柱直径越大越密集，试件的承载力、抗裂性能、刚度均显著提升，试件的整体性能越强，其破坏形态更加接近普通混凝土板的受弯破坏；而短柱较稀疏时，试件的整体性能降低，短柱处的集中应力越明显，裂缝分布较分散。

c.利用ABAQUS对试验板进行了有限元模拟分析，有限元计算结果与试验结果吻合较好。并对影响试件承载能力的相关参数进行有限元模型分析，总结了底板纵筋配筋率，顶底板的厚度、板的高度以及不锈钢短柱对试件抗弯性能的影响规律，实际运用中，建议通过改变板的高度以及短柱的尺寸来合理提高板的抗裂性能和极限承载力。